[데이터마이닝] Scoring, Term Weighting and Vector Space Model (VSM) 1

JAEYOON SIM·2022년 5월 26일

Data Mining

목록 보기

22/23

지금까지 많은 data mining 기법들에 대해서 알아봤는데, 이번에는 이러한 기법들이 실제로 어떻게 text에 적용되는지 알아보고자 한다. Text가 핵심이기 때문에 우리는 많은 word가 존재하는 document가 있다고 가정해보려고 한다. 그리고 이러한 document가 여러개 존재할 수 있을 것이다. 우리는 document에 존재하는 word를 term이라고 지칭할 것이다. 기본적으로 우리가 하고자 하는 것은 이 document를 vector space에 나타내는 것이다. 각각의 document는 feature space에서 일종의 점으로 표현될 것이다. 왜냐하면 각 document는 vector로 표현이 가능하기 때문이다. 이렇게 vector space에 나타내면 서로 similar한지 비교도 가능하고 기존의 data mining 기법들을 쉽게 적용해볼 수 있게 된다. 그리고 비교가 가능하다는 것은 이들을 classification하는 것이 가능해진다 것을 의미하기도 한다. 대표적으로 spam인지 아닌지가 예시가 될 수 있다. Positive document인지 negative document인지를 판단해서 spam mail을 classification할 수 있고, 이와같이 최근에는 여러 text data를 사용하는 사례들도 늘어나고 있다. 사실 이러한 data를 사용하는 분야로 natural language processing(NLP)를 예시로 생각해볼 수 있다.

Ranked Retrieval

먼저 document가 2개 존재한다고 가정하고 이들을 비교해보고자 한다. 그래서 이 document가 서로 맞는지 틀린지를 판단하려고 한다. Ranked retrieval은 일종의 search engine과도 같다. 우리가 구글과 같은 검색엔진에 특정 단어를 검색하면 이와 관련된 여러 document를 볼 수가 있다. 여리 리스트로 나오는 여러 document는 우리가 입력한 단어와 맞는 내용들로 구성되어 있을 것이다. 그래서 document가 입력한 query와 맞는지 틀린지를 판단하기에 이는 boolean과 같은 것이다. 그래서 이러한 것을 우리는 boolean search라고 하는 것이다. 그리고 이러한 결과는 그들의 수요에 대하여 정확한 이해를 가지는 사용자들에게 좋을 것이다. 그래서 우리는 여러 결과들을 가지고 있고, 검색 결과에 대한 정확한 이해를 동반하고 있다면 어떠한 링크를 눌러야하는지 아는 것이다. 그래서 특정 검색어와 관련해서 정확한 이해를 가지고 있으면 많은 document들이 있다고 하더라도 필요한 정보를 얻을 수가 있는 것이다.

이러한 boolean search는 대다수의 사용자들에게는 좋지 못할 것이다. 가령 정확한 이해를 동반한 사용자의 경우에는 document가 많을지라도 필요한 내용을 쉽게 찾을 수 있지만, 그렇지 못한 사용자의 경우에는 많고 많은 document 속에서 필요한 정보를 쉽게 얻기는 힘들 것이다. 그래서 대부분의 사용자들은 boolean query들을 작성할 수 없을 것이다. 대부분은 수없이 많은 결과들을 보고 처리하기를 원하지 않을 것이다. 우리는 오직 매우 유용한 것들로부터 좋은 결과만을 얻기를 원할 것이다. 그리고 이것은 특히 web search에 있어서 해당하게 된다.

Problem with Boolean Search: Feast of Famine

Boolean search는 기본적으로 우리가 입력한 키워드와 관련한 모든 document를 보여주게 된다. 여기서 생기는 문제를 우리는 feast 혹은 famine이라고 부를 것이다. 여기서 feast의 의미는 too many이고, famine의 의미는 too few이다. 우리는 너무 많은 결과를 얻거나 너무 적은 결과를 얻는다는 것이다. 간단하게 web search를 생각해보면 너무 적은 결과를 볼 때도 있으며 너무 많은 결과를 볼 때도 있을 것이다. 다음의 예시를 보도록 하자.

"standard user dlink 650" : 200,000 hits
"standard user dlink 650 no card found" : 0 hits

Boolean search를 이용할 때 키워드를 적게 입력하면 많은 정보를 얻지만, 여기에 다른 키워드를 추가하기만 해도 정보를 얻지 못할수도 있는 것이다. 관리가 가능한 조회 수를 생성하는 query를 작성하려면 많은 기술이 필요하게 된다. 결과적으로 boolean search는 어찌됐는 너무 많은 정보를 주거나 너무 적은 정보를 주는 문제를 가지고 있다. 너무 극단적인 결과를 제공해주기 때문에 우리는 좀 더 soft한 방법을 찾게되는 것이다.

Ranked Retrieval Models

그래서 생각해낸 방법이 ranked retrieval인 것이고, 여기서는 더이상의 boolean은 존재하지 않는다. Query를 만족하는 document들 보다도 ranked retrieval에서는 물론 많은 양의 리스트를 제공해주기는 하지만 여기서 핵심은 어떠한 기준이든 순서를 매김으로써 정보를 제공해준다는 것이다. 가령 입력한 query와 관련하여 관련된 정도가 큰 순서대로 그 결과를 제공해줄 수 있는 것이다. 이렇게 순서대로 정보를 제공해주면 가장 위에 있는 document를 클릭해서 정보를 얻기만 하면 되기 때문에 이전보다 더 나은 방법이라고 할 수 있다. 그리고 이러한 방식이 대부분의 검색엔진을 제공해주는 회사들이 사용하는 방식인 셈이다.

Free text queris라는 것은 연산자와 표현식의 query 언어 대신, 사용자의 query는 인간 언어의 하나 이상의 단어일 뿐이라는 것이다. 원칙적으로 2개의 선택지가 존재하게 된다. 그러나 현실에서 rank retrieval은 일반적으로 free text queries와 관련이 있거나 그 반대일 것이다.

Feast or Famine: Not a Problem in Ranked Retrieval

시스템이 ranked result들을 만들어낸다면, 여기서는 굳이 많은 양의 result들이 문제가 되진 않을 것이다. 아무리 양이 많다고 하더라도 순서가 존재하기 때문이다. 우리의 query와 관련이 없는 아래쪽의 document들은 굳이 볼 필요가 없을 것이다. 그렇기 때문에 결과의 크기는 더이상 문제가 되지 않으며, 1000개의 결과를 보여주더라도 위쪽의 10개 정도만 봐도 충분하게 되는 것이다. Ranked retrieval의 중요한 가정으로는 ranking algorithm이 동작해야 한다는 것이다. 만약 ranking algorithm이 무작위로 동작하게 된다면 ranked retrieval을 사용하지 않는 것과 동일할 것이다.

Scoring as the Basis of Ranked Retrieval

그래서 우리는 score에 대한 notion을 정해줘야 한다. Query에 따라서 document의 rank를 정해줘야 한다. 우리는 이러한 rank를 정해주기 위해서 scoring 시스템이 필요한 것이고, 이는 우리의 query와 document 사이의 similarity를 통해서 score를 정해주고자 한다. 우리는 검색하는 사람들에게 가장 유용하도록 document를 순서대로 제공해주기를 원한다. 그리고 이는 query와 document 사이의 similarity measure를 정의함으로써 가능해지게 된다.

Similarity measure를 기반으로 각 document에 0에서 1사이의 score를 할당해줌으로써 해당 query와 관련하여 document들의 순서를 매겨줄 수 있게 된다. 일반적으로 0과 1사이의 score를 정해주는데, 여기서 0은 완전히 내용이 다르다는 의미이고, 1은 완전히 내용이 일치한다는 의미이다. 결국 similarity measure를 잘 정의해서 document들과 query가 얼마나 일치하는지를 잘 측정해서 score를 정해주면 되는 것이다.

Take 1: Jaccard Coefficient

이러한 방법 중 하나로 Jaccard coefficient가 있다. Jaccard coefficient는 2개의 set의 similarity를 측정할 때 사용하는 일반적인 방법이다. 2개의 set A와 B가 있다고 했을 때, similarity를 측정해주는 Jaccard coefficient는 다음과 같이 정의가 된다.

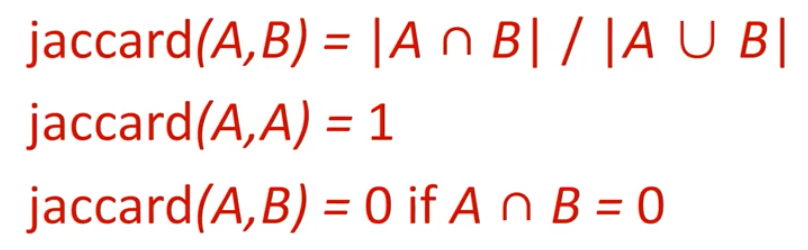두 set의 교집합의 크기를 합집합의 크기로 나눠주면 된다. A와 B는 여러 단어들로 구성되어 있을 것이고, 만약 두 set가 완전히 동일하다면 Jaccard coefficient 값은 1이 될 것이고, 완전히 동일하지 않다면 Jaccard coefficient 값은 0이 될 것이다.

Query : POSTECH admission
Document : I go to KAIST

만약 위와 같이 query와 document가 존재한다면, 어떠한 단어도 일치하지 않기 때문에 Jaccard coefficient 값은 0(=0/6)이 될 것이다. 여기서 보다시피 두 set A와 B는 크기가 같지 않아도 상관이 없다. 즉, 단어의 개수가 서로 달라도 Jaccard coefficient를 계산할 수 있다는 것이다. 그리고 이 값은 항상 0과 1 사이로 결정이 될 것이다. Text data는 항상 동일한 크기를 가지고 있지 않기 때문에 이러한 measure는 더욱 효과가 있는 것이다. 추가로 다음의 예시에서 query-document match score를 Jaccard coefficient를 이용해서 구해볼 수 있다.

Query : ides of march
Document1 : caesar died in march
Document2 : the long march

여기서 "march"라는 단어는 모두 가지고 있다. Jaccard coefficient를 구해보면 document1에서는 1/6이고, document2에서는 1/5이 되는데, 사실상 이정도의 값은 매우 유사하다고 이야기할 수 있다.

Issues with Jaccard for Scoring

하지만 이러한 Jaccard coefficient를 사용해서 scoring을 하는데 있어 몇가지 issue들이 존재한다.

It doesn't consider term frequency

Document 안에 동일한 단어가 얼마나 사용되었는지는 고려하지 않는다.

Rare terms in a collection are more informative than frequent terms. Jaccard doesn't consider this informatioon

Document에서 여러번 등장하는 단어보다도 적게 등장하는 단어가 더 많은 정보를 가지고 있다고 판단할 수 있는데, Jaccard coefficient는 이러한 정보는 전혀 고려하지 않는다. 예를 들어서 누군가의 이름이 굉장히 드물다면, 그 이름은 그 사람을 설명해주는 특징이 될 것이다. 반대로 누군가의 이름이 굉장히 흔한 이름이라면, 이 이름은 그만큼 정보를 많이 가지고 있지 않게 될 것이다.

Query-Document Matching Scores

이러한 issue들이 존재하기 때문에 우리는 Jaccard coefficient 대신에 length를 normalization할 수 있는 더 정교한 방법이 필요한 것이다. 우리는 이제 query/document pair에 대한 score를 할당해주는 방법이 필요하다. Query와 document 각각에 대한 score 대신에 query/document pair에 대한 score를 정해보고자 하는 것이다. 이를 위해서 먼저 하나의 단어인 one-term query로 시작해보자. 만약 query term이 document에 존재하지 않는다면 score는 반드시 0이 되어야 한다. 이 score는 query term이 document 안에 더 많이 존재할수록 올라가야 한다.

여기서 혼란스러워하지 말아야 할 내용이 있다. 예를 들어 term이 2개가 있다고 했을 때, 첫번째 term이 두번째 term보다 더 정보가 많다고 해보자. 하지만 두번째 term은 더 많은 빈도수로 document에 등장한다고 해보자. 이때 각 term에 대한 중요도를 나타내는 importance가 존재할 것이고, 빈도수를 나타내는 frequency가 존재할 것이다. 그래서 지금은 하나의 term에 대해 이야기하고 있지만, 여러개의 term이 있다고 했을 때 각각의 term은 중요도와 빈도수가 다르게 측정될 수가 있다. 여기서는 하나의 term이 document에 많이 등장하면 등장할수록 score를 더 높게 측정해야 된다는 이야기다.

Recall: Binary Term - Document Incidence Matrix

다음의 예시를 보도록 하자.
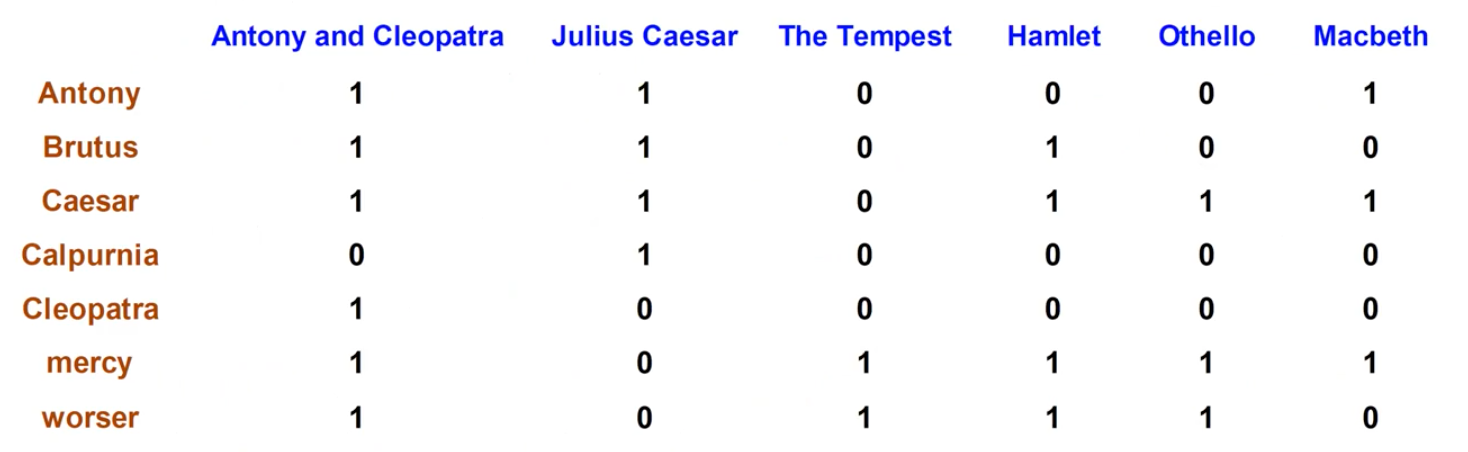여기서 여러개의 term이 row로 존재하고 각 term은 column으로 존재하는 여러 document에 해당 term이 등장하는지를 1과 0으로 나타낸 것이다. 이렇게 boolean search를 통해서 각 term이 등장하는지를 1과 0으로 나타내게 되면, 문제는 각 term이 어떠한 document에서 중요한지를 쉽게 판단할 수 없다는 것이다. 우리는 오로지 어떠한 document와 연관성이 있는지만 판단할 수 있고, 얼마나 중요한지는 판단하기 어렵다는 것이다. 그래서 우리는 이러한 matrix를 document incidence matrix라고 하여 존재성만 어느정도 판단할 수 있게 된다.

Term-Document Count Matrix

그래서 이번에는 얼마나 등장했는지를 판단하고자 한다.
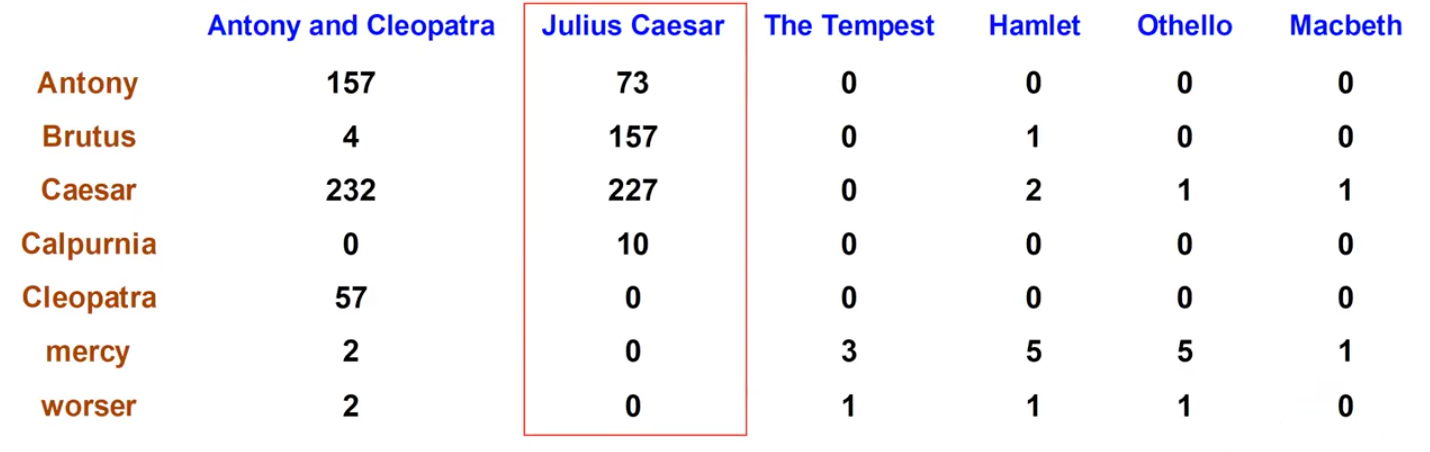위의 matrix를 통해서 각 term이 document에 얼마나 등장하는지를 판단할 수 있다. Incidence matrix에서는 등장하면 1이었지만, count matrix에서는 얼마나 등장하는지를 해당 숫자로 나타낼 수 있다. 그래서 이 matrix에서 각 document는 7차원의 counter vector가 되어 각 term의 빈도수를 설명할 수 있게 된다.

Bag of Words Model

이러한 vector representation을 우리는 bag of words model이라 부른다. 각 document를 bag으로 생각하면 각각의 bag에는 해당 document에 등장하는 단어들이 빈도수만큼 들어있게 되는 것이다. Bag of words model의 흥미로운 점은 document안에 있는 단어들의 순서를 고려하지 않는다는 것이다. 다음의 예시를 보도록 하자.

John is quicker than Mary
Mary is quicker than John

위의 두 예시를 이해해보면 완전히 반대되는 의미를 가지고 있다. 하지만 그저 단어의 빈도수를 확인해보면 동일하게 되고 순서는 전혀 고려하지 않고 있다. 그래서 bag of words model에서는 위의 두 문장은 동일한 vector를 만들게 되고, 이는 오로지 frequency만을 고려하겠다는 이야기다. 어떠한 의미에서 이는 한걸음 후퇴를 의미하기도 한다. 우리는 text data를 효과적으로 나타내기 위해서 information을 버리고 있는 것이다. 하지만 그래도 bag of words model은 잘 동작할 것이다. Bag of words model은 이러한 term들의 빈도수를 구하고 text data를 count matrix로 변형시킬 때 순서, 즉 positional index라는 개념을 잃어버리게 되는 것이다.

Term Frequency tf

우리는 bag of words model에 대해서 이야기하면서 얼마나 자주 term들이 등장하는지를 구할 필요가 있다. 그래서 이를 우리는 term frequency, tf라고 부를 것이다. $\text{tf}_{t,d}$ 라고 표기하게 되면 이는 document d 안에 존재하는 term t의 빈도수를 나타내게 된다. 우리는 이러한 tf를 query-document match score를 계산할 때 사용하고자 한다.

우리는 raw term frequency는 원하지 않는다. 왜냐하면 어떠한 term이 10번 등장하는 document가 1번 등장하는 document보다 더 관련성이 있기 때문이다. tf가 10인 경우가 tf 1인 경우보다 중요하기는 하지만 10배 더 중요하다는 것은 아니다. 그래서 여기서 중요한 것은 relevance가 tf가 증가한다고 해서 비례적으로 증가하는 것은 아니라는 것이다.

Log-Freqeuncy Weighting

앞서 10배 더 등장한다고 10배 더 중요한 것이 아니라는 이야기를 했다. 그래서 사람들은 이러한 tf에 log를 취해서 weighting을 하고자 했다. Document d에 존재하는 term t에 대한 log frequency weight는 다음과 같이 정의할 수 있다.

w_{t,d}=\begin{cases}1+\text{log}_{10} \text{ tf}_{t,d} &&\text{if tf}_{t,d}>0\\0 &&\text{otherwise} \end{cases}

Weight $w$ 는 만약 tf가 0이 아니라면 log를 취해주고 1을 더하면 되고, 이 경우가 아니라면 0이 될 것이다. 만약 tf가 0이면 weight가 0이고, tf가 1이면 weight는 1이 될 것이다. tf가 2가 되면 weight는 1.3 정도가 될 것이고, weight가 10이면 2, 1000이면 4가 될 것이다. 이렇게 term이 등장하는 빈도수를 그대로 반영하는 것이 아닌 log를 취해서 얼마나 중요한지를 판단할 수 있게 된 것이다. 1000번 등장하는 term이 1000배 중요한 것이 아닌 4배 정도 중요하다고 weighting을 한 것이다.

이제 document-query pair에 대한 score를 매겨보고자 한다. 우리는 지금까지 하나의 document에 대한 하나의 term에 대해서 알아보았다. 그렇다면 하나의 query에 1개 이상의 term이 있다면 어떻게 될까? 이러한 경우에는 query $q$ 와 document $d$ 모두에 존재하는 term $t$ 를 더해주면 된다.

\text{score} = \sum_{t\in q\cap d}(1+\text{log tf}_{t,d})

이 score는 어떠한 query term도 document에 존재하지 않을 경우에는 0이 될 것이다.

Rare terms are more informative

Rare term이 frequent term보다 더 정보를 가지게 된다. 앞서 빈도수가 큰 term이 더 중요한 것과 같이 score를 계산했었다. 혼란스러워하지 말아야하는 부분은 더 빈번하게 등장하는 중요한 term이 중요한 것이다. 필요하지 않은 term이 많이 등장한다고 해서 score를 계산하는데 기여하지는 않는다. 예를 들어 stop word가 있을 수 있다. 영어에서 a, an, the, of와 같은 단어들은 자주 등장하지만 중요하지는 않다. 여기서 rare term이라고 하는 것은 query와 document를 characterization할 수 있는 term을 이야기하고, 이러한 단어들이 중요한 것이다. 그래서 이러한 단어들이 포함된 document의 경우 해당 단어를 포함하는 query와 더 관련이 있을 가능성이 있다. 그래서 우리는 이러한 rare term에 더 높은 weight를 주기를 원하는 것이다.

정리하자면 여러 document에 걸쳐서 드물게 등장하는 단어가 정보가 더 많은 것이고, 우리는 이러한 rare term을 각 document에 더 자주 등장하도록 하기를 원하는 것이다. 이러한 상황이 만족이 되면 score를 구하는게 더 쉬워지게 될 것이다.

Collection vs. Document Frequency

이번에는 2개의 frequency에 대해서 비교해보고자 한다. 하나는 collection frequency이고 다른 하나는 document frequency이다.

Collection frequency of t : the number of occurences of t in the collection
Document frequency of t : the number of documents in which t occurs

Term $t$ 에 대한 collection frequency의 경우 document collection에 존재하는 $t$ 의 빈도수를 나타낸다. Document가 여러개가 있어 collection을 만들고 있다면, 모든 document로부터 빈도수를 구한 것이다. 반면, document frequency는 $t$ 가 존재하는 document의 수를 나타낸다. 1000개의 document가 있다고 했을 때, "the"라는 term은 많은 document에 존재할 것이기에 document frequency가 클 것이다. 반면, 특정 단어의 경우에는 많이 존재하지 않아 document frequency가 작을 것이다. 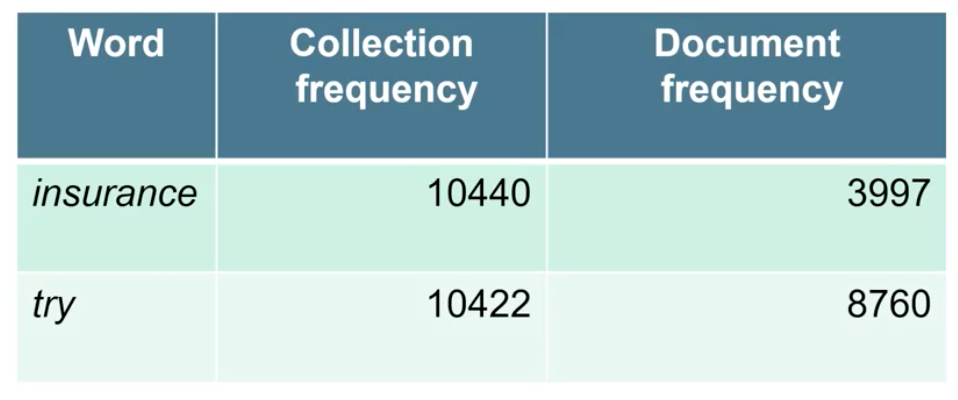위의 예시를 보도록 하자. 여기서 insurance라는 term은 try라는 term보다도 더 구체적인 단어이다. Document의 collection이 주어졌을 때, collection frequency를 보면 두 단어가 매우 비슷한 것을 확인할 수 있다. 하지만 document frequency를 보면 insurance가 try보다도 더 적은 것을 볼 수 있다. 이것이 의미하는 것은 모든 document에 걸쳐서 insurance와 try라는 단어가 비슷하게 자주 등장하는 것은 collection frequency를 통해서 확인할 수 있다. 그래서 이것만으로 우리는 어떠한 단어가 더 중요한지 쉽게 이야기하기 어렵다. 하지만 document frequency를 보면 insurance가 더 드물게 존재하는 것을 확인할 수 있다. 이를 기반으로 우리는 insurance가 더 informative하다고 이야기할 수 있다. 그래서 우리는 이를 기반으로 어떠한 단어가 검색하는데 더 나은지에 대해서 더 높은 weight를 부여할 수 있게 된다.

idf Weight

이러한 아이디어를 하나로 합치기 위해서 사람들은 inverse document frequency(idf)를 생각했다. 이를 만들어낸 이유는 앞서 rarity를 measure에 합치기 위해서이다. 드물게 등장하는 단어는 document에서 잘 보이지 않기 때문에 더 informative하다. 이를 정의하기 위해서 먼저 document frequency를 $\text{df}_t$ 로 정의하고자 한다. $\text{df}_t$ 는 $t$ 의 정보력에 대한 inverse measure로, $t$ 가 중요하다면 어디서든 쉽게 보이지는 않을 것이다. 그리고 물론 $\text{df}_t$ 는 전체 document의 개수 $N$ 보다 크진 않을 것이다. 우리는 이제 idf를 다음과 같이 정의하고자 한다.

\text{idf}_t = \text{log}_{10}(N/df_t)

전체 document의 개수를 $\text{df}_t$ 로 나눠주고 log를 취해주게 되면, 이 식이 바로 idf 식이 되는 것이다. Stop words를 생각해보면 N을 $\text{df}_t$ 로 나눴을 때 그 값은 0에 가까워지게 될 것이다. 반면, 특정 rare term의 경우에는 log 안의 값이 커져 전체적으로 idf 값은 큰 값이 될 것이다. 이 식에서 $N/\text{df}_t$ 대신에 log를 취해주는 이유는 idf의 효과를 어느정도 떨어뜨리기 위해서이다. 다음의 예시는 $N$ 이 100만일 때의 idf를 구한 예시이다.

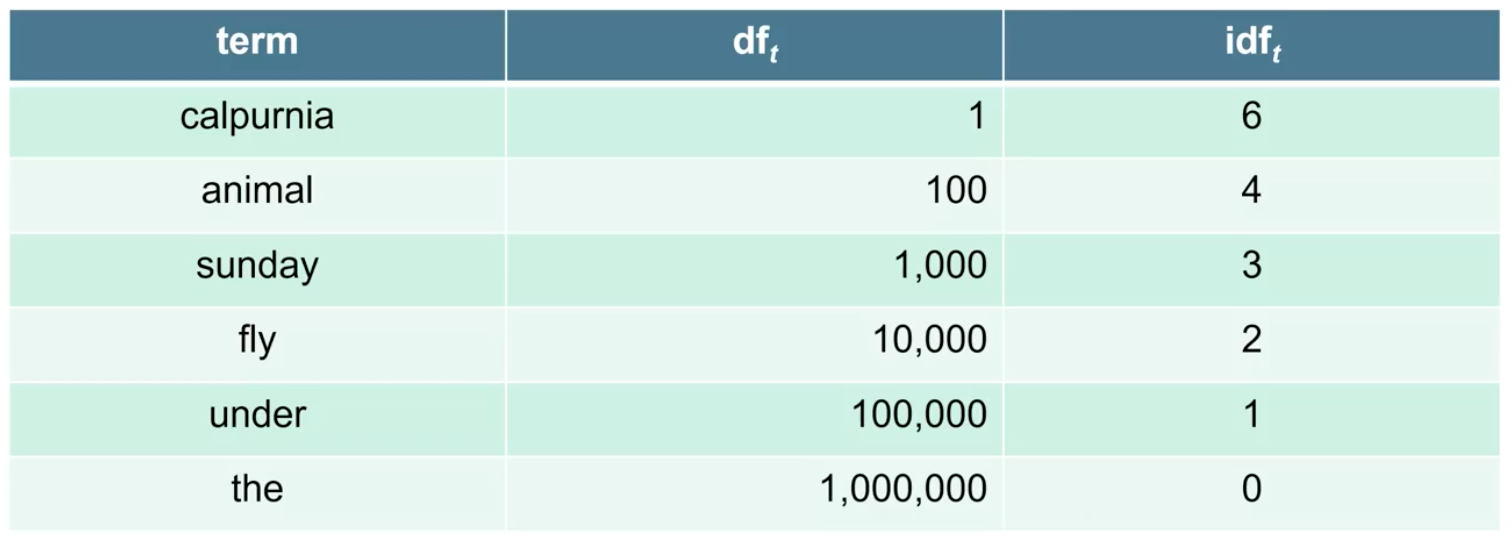"the"의 경우 모든 document에 존재하기 때문에 $\text{df}_t$ 가 100만이 되고 idf는 log1이 되어 0이 될 것이다. 그리고 당연하지만 document의 collection이 달라지게 되면 idf 값도 달라지게 된다. Collection마다 각각의 term $t$ 에 대해서 하나의 idf 값을 가지게 되는 것이다.

Effect of idf on ranking

지금까지 term와 document pair, 그리고 term과 collection pair에 대해서 이야기해봤다. 후자의 경우에는 term이 얼마나 중요한지를 설명할 수 있다. 반면, 전자의 경우에는 term이 해당 document 안에서 얼마나 중요한지를 설명할 수 있다. 이후에는 이 모든 내용을 하나로 합칠 것이지만, 그 전에 ranking에 대한 idf의 효과에 대해서 알아보고자 한다.

하나의 단어가 포함되어 있는 one-term query들에 대해서 idf가 가지는 ranking의 효과에 대해서 생각해봤을때, 사실 idf는 하나의 term query들에 대해서는 ranking을 매기는 효과는 존재하지 않는다. 왜냐하면 비교할 대상이 존재하지 않기 때문이다. idf는 적어도 2개의 term이 있는 query에 대해서 document의 ranking을 매길 수가 있다. "capricious person"이라는 query에 대해서 idf weighting은 아무래도 최종 document ranking에서 person보다 capricious를 더 중요하게 여기게 된다.

tf-idf Weighting

우리는 이제 term frequency와 informativeness를 한번에 합치는 tf-idf weighting 기법에 대해서 알아보고자 한다. 지금까지 term과 document에 대해서는 얼마나 자주 해당 단어가 document에 등장하는지에 관심을 가졌다. 이후에 전체 document collection에서 우리는 해당 term이 얼마나 중요한지를 고려할 필요가 있었다. 그렇기 때문에 우리는 tf와 idf라는 개념을 통해서 각각 알아보았고, 이번에는 이를 통합한 tf-idf weighting에 대해서 알아보려고 한다. 하나의 term에 대해서 tf-idf weight는 다음과 같이 tf weight와 idf weight의 곱으로 정의할 수 있다.

w_{t,d} = \text{log }(1+\text{tf}_{t,d}) \times \text{log }_{10}(N/\text{df}_t)

이렇게 식이 구성되면 2개 모두에서 높은 값을 얻어야 전체적인 weight 값 마저도 높게 얻을 수가 있다. 두 condition을 모두 만족시켜야 하기 때문에 document에서 해당 단어가 자주 등장해야함과 동시에 중요해야 term과 document가 서로 관련이 있다고 이야기할 수 있다. tf-idf weighting 기법은 몇전에는 information retrieval에서 최고의 weighting 기법이었지만, 아마 여전히 최근에도 잘 동작하는 weighting 기법일 것이다. 우리는 tf-idf weighting을 tf.idf 혹은 tf x idf로도 부를 수 있다. 그리고 tf-idf weighiting은 document 내에 빈도수가 늘어나게 되면 그 값도 증가하게 될 것이다. 마찬가지로 이 값은 collection 내에서 해당 term의 rarity와 함께 증가하게 될 것이다.

Score for a Document given a Query

Query $q$ 와 document $d$ 가 있을 때, 이들을 비교하기 위해서 score를 구하여 최종적으로 ranking을 얻어야 한다. 이를 위해서는 query와 document에 걸쳐 많은 term들이 있어야 한다. Query와 하나의 document가 주어졌을 때, 양쪽 모두에 존재하는 term들이 여러개가 있을 때에는 해당하는 모든 term들에 대해서 tf.idf score를 더해주면 된다.

\text{score}(q,d) = \sum_{t\in q\cap d} \text{tf.idf}_{t,d}

위와 같은 식을 사용해도 되지만, 이는 하나의 방법이고 다양한 variant들이 존재할 수 있다. 우리는 초반에 incidence matrix를 통해서 boolean search를 이용하여 존재성을 1과 0으로 나타냈었다. 이후에는 frequency를 나타내는 count matrix도 살펴보았다. 이러한 counting으로부터 idf를 생각하기 위해서 document collection을 고려하게 되면 우리는 다음과 같이 tf-idf weight matrix를 얻을 수 있다.
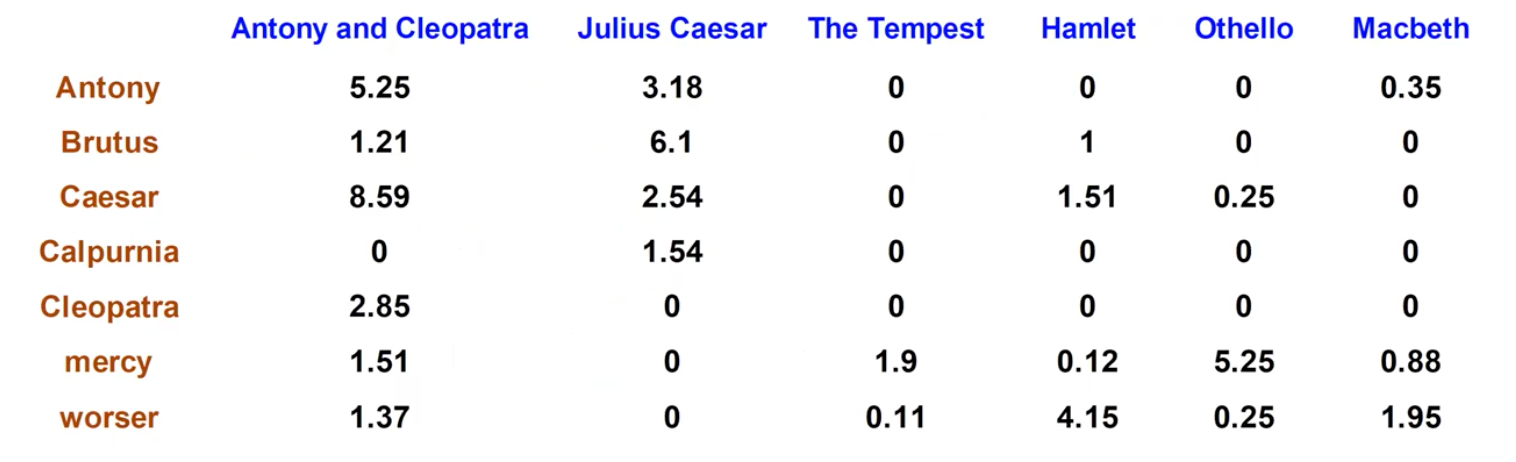각 document는 이제 tf-idf weight를 설명하는 real-valued vector에 의해서 나타낼 수가 있다. 이렇게 document를 vector로서 표현하게 되면 우리는 앞으로 어떠한 data mining algorithm을 적용할 수가 있게 된다. 이러한 방식이 text mining이 동작하는 원리이다.