[데이터마이닝] Supervised vs. Unsupervised Learning - Unsupervised Learning

JAEYOON SIM·2022년 3월 24일

Data Mining

목록 보기

8/23

Unsupervised Learning Process

Representation of Objects in Machine Learning

Data로부터 어떠한 것들을 학습할 수 있는지 알아보려고 한다. 학습의 경우 크게는 supervised learning과 unsupervised learning으로 나눌 수 있다. 이 중에서 unsupervised learning은 data $x=(x_1, x_2, \dots, x_N), x_i\in\mathbb{R}^k$ 가 주어졌을 때, 이 data로부터 어떠한 pattern을 찾는 것이 목적이다. $k$ 개의 attribute가 존재하는 data matrix로부터 우리는 어떠한 pattern이든지 찾아내야 한다. Data matrix에서 특정 object에 해당하는 instance $x _i$ 의 경우 $k$ 차원의 feature들로 표현할 수 있다. 그래서 각 $x_i$ 는 $k$ 차원의 feature space 혹은 attribute space에서 특정 coordinate로 존재할 것이다. 이러한 과정을 feature representation이라 하고, 이를 통해서 data가 feature space에서 어떻게 생겼는지 파악할 수 있다.

예를 들어, 글자들이 존재하는 document의 경우 단어의 빈도 수로 표현할 수 있고, image의 경우에는 color histogram, medical information의 경우에는 medical test result 등으로 표현할 수 있다.

Training

Unsupervised learning에 앞서 learning의 관점에서 봤을 때 data matrix로부터 무언가를 학습한다는 것은 어떠한 pattern을 찾고자 하는 것이다. 그리고 unsupervised learning이 되면 어떠한 supervision 없이 학습을 통해서 pattern을 찾아내야 한다. 여기서 무언가를 학습한다고 했을 때 가장 중요하게 필요한 것은 바로 training data이다.

Training data는 training 단계를 위한 instance 혹은 object들의 집합이고, 일반적으로는 unknown distribution을 가정하고 data sampling을 진행한다. 즉, independent and identically distributed(i.i.d) 조건을 만족한다고 생각하고 학습을 진행한다. 이 조건은 data universe라는 곳에 무수히 많은 data가 존재한다고 했을 때, $N$ 개의 sample을 뽑아서 이들이 모두 같은 data universe로부터 왔다고 가정하겠다는 것이다. 그리고 이 중에서 서로는 서로에게 영향을 주지 않는 independent 조건을 만족한다고 가정하게 되는데, 하나를 sampling하게 되면 이 결과가 다음 sampling에 영향을 주지 않게 된다.

Testing

Training을 하게 되면 특정 pattern을 배우게 되는데 이를 이용해서 testing에서는 이전에 보지 않던 data로부터 미래의 결과를 예측하게 된다. 예를 들어 inference나 estimation과 같은 task들이 unsupervised learning에 해당하게 된다.

With Unsupervised Learning

Unsupervised learning에서는 어떠한 label도 가지지 않고 오로지 data만을 가지게 된다. 여기서 label은 흔히 supervision이라 부르고, label이 존재하게 되면 supervised learning이 되는 것이다.

x_i = \underbrace{[ O,O,O,\dots ]}_{attributes},\qquad y_i = ?

Label이 없기 때문에 학습을 통해서는 data가 어떻게 생겼는지만을 학습하게 된다. 예를 들어 data의 shape이나 distribution과 같이 특정 label을 학습하는 것이 아닌 data 자체의 생김새를 학습하는 것이다.

Let's try to

그렇게 observation들의 finite set이 주어지게 되면 이로부터 probability distribution을 modeling해야 한다. 그래서 data universe로부터 sampling한 data object들을 학습을 하고, 이를 기반으로 data universe가 어떻게 생겼는지 추정할 수 있어야 한다. Density estimation, clustering, dimension reduction, anomaly detection과 같은 task들이 여기에 해당하며 이러한 task들은 어떠한 supervision 없이도 가능하다. 그럼 unsupervised learning이 하고자 하는 것이 무엇인지 다음의 간단한 예시를 통해 살펴보도록 하자.

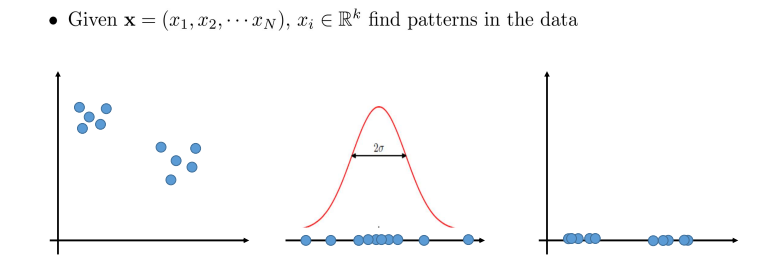$N$ 개의 sample이 $k$ 개의 attribute와 함께 주어졌을 때, data sample들이 좌측과 같이 cluster를 형성할 수 있다. 위의 경우는 2차원으로 2개의 attribute에 대하여 cluster를 형성하고 있는 상황이다. 이러한 data를 1차원에서 보게 되면 distribution 중간에 밀집되어 분포하는 것을 볼 수 있다. 중간이 dense하고 끝이 sparse하게 분포하게 되는 이유는 i.i.d 가정에 의한 것이고, 이를 우측과 같이 1개의 attribute에 관해서만 clustering을 하고 싶을 때 2차원 상에서 1차원으로 하나의 axis에 projection해서 볼 수도 있다. 위와 같은 경우에는 여전히 cluster를 형성한다고 할 수 있으며, 이렇게 unsupervised learning을 통해서 좌측의 2차원 상의 data를 1차원 상에 표현하는 dimension reduction을 할 수 있다.

Clustering

Clustering에는 다양한 기법들이 존재하지만 이번에는 많은 clustering 기법들 중에서 간단한 K-means clustering에 대해서 알아보려고 한다. 이 기법은 $K$ 개의 mean들이 존재한다는 것을 의미하는데, 이는 곧 $K$ 개의 cluster를 형성하는 것을 의미하기도 한다. 여기서 mean이라는 것은 결국 cluster의 center가 되는 것이다. 이 기법의 목적은 $K$ 개의 cluster center를 찾아서 각 sample에 information cluster label을 부여하는 것이다. 그래서 K-means clustering의 가정은 다음과 같다.

\text{i.i.d.}\; x=(x_1,x_2,\dots,x_N), x_i\in\mathbb{R}^d \text{ and a parameter }k

즉, data는 동일한 data universe로부터 존재하기 때문에 동일한 distribution을 따라야 한다. 그래서 $d$ 개의 attribute에 대하여 각각의 $x_i$ 를 sample로 가져오고 이와 더불어 hyperparameter로 $k$ 를 사용할 것이다. Data가 주어지고 우리가 특정한 $k$ 를 정함으로써 총 $k$ 개의 cluster를 찾고자 할 것이다. 우리는 obseravtion $N$ 개를 각 observation에서 가장 가까운 mean을 가진 cluster에 속하는 $k$ 개의 cluster로 분할하고자 한다. 그래서 2개의 cluster에 대해서 각 cluster의 center가 $C_1,C_2$ 라고 했을 때, data sample로부터 각각의 cluster center와의 distance를 구해서 더 짧은 곳에 해당하는 cluster에 해당 data sample을 포함시키겠다는 것이다.

이를 구하는 가장 naive한 방식은 무한히 많은 for loop를 이용해서 거리를 구해서 비교하면 된다. 물론 이렇게 하면 data의 크기가 큰 경우에는 굉장히 많은 시간이 소모될 것이다. 이렇게 하더라도 optimal solution을 구하기는 어려울 것이지만 optimal solution에 매우 가깝게는 구할 수 있을지도 모른다. 즉, NP-hard problem이지만 heuristics는 존재할 것이라는 이야기다. 그리고 K-means clustering을 K-nearest neighbor classification과 동일한 것으로 착각하면 안된다. 그렇다면 K-means clustering은 어떠한 과정으로 진행이 될까?

가장 먼저 $d$ 차원 공간에서 data $x=(x_1,x_2, \dots, x_N)$ 이 주어졌을 때, initialization 과정으로 무작위로 $k$ 개의 cluster center를 선택한다. 이후에는 assignment step과 update step이 convergence를 만족할 때까지 반복될 것이다. Assignment step에서는 각각의 point $x$ 에 대해서 모든 center들과의 distance를 구해서 가장 적절한 cluster를 결정해주게 된다. 즉, 각각의 $x_i$ 들에 대해서 가장 짧은 distance에 해당하는 cluster $c_k$ 를 할당해주는 것이다. 그리고는 처음에 무작위로 설정했던 $k$ 개의 cluster center를 모두 update 시켜야 한다. Assignment step을 하고 나면 각각의 cluster center에 모든 $x$ 가 연결되어 있을 것이다. 무작위로 설정된 center이기에 정확하지 않을 것이고 그렇기 때문에 새로운 cluster center를 결정해줘야 한다. 이는 다음과 같이 mean을 취해서 결정해주면 된다.

c_i^{t+1} = \frac{1}{|S_i^t|}{\sum_{x_j\in S_i^t}x_j}

각 cluster마다 해당하는 data sample들을 이용해서 mean을 구하고, 구한 결과를 해당 cluster의 새로운 center로 바꿔줘야 한다. 매 반복마다 $k$ 개의 cluster가 생길 것인데, 현재 clustering의 결과를 이용해서 새로운 clustering으로 update 해가는 것이다. 이러한 과정을 convergence를 만족할 때까지 진행하다보면 전체적인 clustering이 끝날 것이고, $k$ 의 값이 점점 커지게 되면 더 많은 반복문을 거쳐야할 것이다.

그렇다면 이는 항상 convergence를 만족할 것인가? 답은 yes이다. 하지만 global optimal을 찾았다고는 보장할 수 없을 것이다. 그렇다고는 해도 global optimal에 근접한 결과는 얻을 수 있다. 그리고 initialization에서 cluster의 center는 예상되는 결과와 비슷할수록 좋고, 우리가 결정해야 하는 $k$ 는 우리의 domain knowldege나 만약 supervision이 주어진다면 error를 줄일 수 있는 방향으로 설정하는 것이 좋다.

Maximum Likelihood Estimation(parametric)

Likelihood function

Clustering을 어떻게 하는지 K-means clustering을 통해서 어느정도 알았다면, 이제부터는 distribution을 어떻게 추정할 수 있는지 알아볼 것이다. 여기에는 parametric method와 non-parametric method가 존재하며, parametric이라는 것은 model이 주어진 경우를 이야기한다. 여기서 model을 parametric model로 이는 Gaussian, Bernoulli 등과 같이 statistical한 경우를 이야기 한다. Gaussian distribution은 너무나도 유명한 distribtuion으로 다음과 같이 생겼다.
Gaussian distribution은 mean을 나타내는 $\mu$ 와 variance을 나타내는 $\sigma^2$ 라는 2개의 parameter를 가지고 있다. 즉, 이 2개의 parameter를 통해서 Gaussian distribution을 추정할 수 있다는 것이다. 이러한 distribution을 추정하기 위해서는 가장 먼저 likelihood function이라는 것을 정의할 필요가 있다. Likelihood function은 data가 주어졌을 때 statistical model의 parameter에 관한 function으로 다음과 같다.

L(\theta;x) = f(x|\theta)

\hat{\theta}(x) = \operatorname*{argmax}_\theta L(\theta;x)

여기서 data $x$ 는 i.i.d를 만족하고 $k$ 차원의 space에서 정의가 된다. 여기에는 어떠한 label도 존재하지 않으며 오로지 주어지는 것은 무수히 많은 data 뿐이다. 그래서 likelihood라는 것은 이러한 data로부터 parameter에 관한 function이다. 자세한 내용은 여기(MLE of ML)를 참고하면 된다. MLE의 목적은 결국에는 data의 likelihood를 최대로 만들 수 있는 model parameter들을 찾는 것이다.

Log-likelihood of a Gaussian distribution

이를 위해서 먼저 할 일은 Gaussian distribution의 likelihood에 log를 취하는 것이다. Likelihood는 위에서 봤듯이 distribution에서 각 $x$ 마다 취하는 값들을 곱한 결과이다. 그리고 이 값은 Gaussian distribution의 식에 각 $x$ 를 대입해준 결과들을 곱한 것과 같다.

L(\mu,\sigma) = p(x|\mu,\sigma^2)=\prod_{i=1}^N N(x_i|\mu,\sigma^2) = \prod_{i=1}^N \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_i-\mu)^2}{2\sigma^2}}

Gaussian distribution의 특징은 쉽게 다루기 어려운 exponential term을 가지고 있다는 것이다. 그래서 likelihood 앞에 log를 취하는 이유가 바로 이러한 이유 때문이다. 그리고 log function의 경우 monotonic increasing function이기 때문에 기존의 목적에 어긋나지 않아 likelihood에 log를 취해도 상관이 없고, optimal parameter의 결과에도 영향이 없다.

\text{ln }p(x|\mu,\sigma^2)=\text{ln}\prod_{i=1}^N N(x_i|\mu,\sigma^2) =\text{ln }\bigg(\prod_{i=1}^N \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_i-\mu)^2}{2\sigma^2}}\bigg)

= \sum_{i=1}^N\text{ln }N(x_i|\mu,\sigma^2) = \sum_{i=1}^N \text{ln }\bigg(\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_i-\mu)^2}{2\sigma^2}}\bigg)

=-\frac{1}{2\sigma^2}\sum_{i=1}^N(x_i-\mu)^2 - \frac{N}{2}\text{ln }\sigma^2 - \frac{N}{2}\text{ln }(2\pi)

Maximum(Log) Likelihood Estimation

이제는 이렇게 얻은 log-likelihood를 최대로 만들어야 한다. 그 방법은 concave function의 critical point를 구하면 된다. Derivative를 구해서 slope가 0이 되는 지점이 log-likelihood function을 최대로 만드는 지점이고, 이 지점의 parameter가 optimal parameter로 우리가 찾고자 하는 결과가 된다.

l(\mu,\sigma) = \text{ln }p(x|\mu\,\sigma^2) = -\frac{1}{2\sigma^2}\sum_{i=1}^N(x_i-\mu)^2 - \frac{N}{2}\text{ln }\sigma^2 - \frac{N}{2}\text{ln }(2\pi)

\mu_\text{MLE}, \sigma_\text{MLE} = \operatorname*{arg\,max}_{\mu,\sigma} \text{ ln } p(x|\mu,\sigma^2)

(1)\; \frac{\partial l}{\partial\mu}=0\quad \Rightarrow \quad\mu_\text{MLE} = \frac{1}{N}\sum_{i=1}^N x_i

(2)\; \frac{\partial l}{\partial\sigma^2}=0\quad \Rightarrow \quad\sigma^2_\text{MLE} = \frac{1}{N}\sum_{i=1}^N(x_i-\mu_\text{MLE})^2

만약 우리의 statistical model이 Gaussian distribution인 경우에는 이 Gaussian distribution을 결정하는 2개의 parameter를 가지게 될 것이고, data에 가장 적절하게 들어맞는 distribution의 모양은 이렇게 MLE를 이용해서 optimal parameter를 찾아주면 된다.

Binary Variable(Bernoulli trials)

MLE는 Gaussian distribution 외에도 여러 distribution에 사용할 수 있다. 결국 여기서 중요한 것은 data 그 자체이고 data가 어떻게 생겼는지와 어떻게 얻었는지에 따라서 결정이 된다. 그래서 이번에는 data가 binary variable인 경우에 대해서 알아보려고 한다. 그중에서도 data가 Bernoulli distribution을 따르는 경우를 보도록 하자. 가장 대표적인 예시는 동전 던지기로 동전의 경우 앞면과 뒷면이 각각 특정 확률로 나올 수가 있다. 앞면이 나오는 경우를 1이라 하고 뒷면이 나오는 경우를 0이라 했을 때, 앞면이 나오는 확률은 parameter $p$ 의 확률로 나온다고 해보자.

p(x=1|p)=p

p(x=0|p)=1-p

$x$ 가 따르는 probability distribution의 경우 Bernoulli distribution이기 때문에 이는 다음과 같이 표현할 수 있다. 이와 관련해서는 여기를 참고하면 된다.

Ber(x|p)=p^x(1-p)^{1-x}

\mathbb{E}[x] = p

var[x] = p(1-p)

이번에는 Bernoulli distribution의 likelihood function을 디자인하는 법에 대해서 알아볼 것이다.
Bernoulli distribution의 likelihood function은 각 case를 위와 같이 모두 곱해주면 된다. 이는 Gaussian distribution에서 likelihood function을 구할 때와 같은 방식이다. 그리고 이를 일반화 하면 다음과 같을 것이다.

L(p;x) =\prod_{i=1}^N p^{x_i}(1-p)^{1-x_i} = p^{\sum_{i=1}^Nx_i}(1-p)^{N-\sum_{i=1}^N x_i}

여기에 log를 취해주면 다음과 같아지고 결과적으로 optimal parameter $p$ 를 구할 수 있게 된다.

l(p;x) = \text{ln }L(p;x) = (\sum_{i=1}^n x_i)\text{ln }p+(N-\sum_{i=1}^N x_i)\text{ln }(1-p)

=N(\bar{x}\text{ln }p + (1-\bar{x})\text{ln }(1-p)) \qquad \text{where }\bar{x}=\frac{1}{N}\sum_{i=1}^N x_i

\frac{\partial l(p;x)}{\partial p} = N\frac{\bar{x}-p}{p(1-p)}

\frac{\partial l}{\partial p}=0 \quad \Rightarrow \quad p^{\ast}=\bar{x}

Density Estimation(non-parametric)

지금까지 본 parametric method와는 다르게 이번에는 non-parametric method에 대해서 알아보려고 한다. Non-parametric density estimation에는 어떠한 statistical model이 prior로 주어지지 않는다. 즉, 어떠한 사전 정보나 지식 없이 순수하게 관측된 데이터만으로 probability density function을 추정하겠다는 것이다. 지금까지 본 MLE의 경우 parameter를 추정해야 하는 parametric density estimation이었다. 하지만 non-parametric density estimation에서는 prior를 제외시키고 data와 parameter의 관계를 파악하고자 한다.

1. Histogram(non-parametric)

그리고 가장 naive한 density estimation 방식으로 histogram이 있다. 관측이 된 data들로 histogram을 만들고 이렇게 구한 histogram을 normalization을 통해서 probability density function으로 사용하겠다는 것이다.

Histogram이라는 것은 domain을 여러개의 bin으로 나눈 것을 이야기한다. 그리고 얼마나 많은 data sample이 각 bin에 존재하는지 간단하게 셀 수 있다. 즉, 우리는 histogram을 통해서 각 bin으로부터 sample들의 frequency를 계산할 수 있다. 그래서 이러한 frequency를 normalization을 거치면 각 bin에 존재하는 sample의 probability를 구할 수가 있고 있다. 다음의 예시는 axis가 0에서 5로 되어 있어 normalization을 하지 않은 결과들이다. 그리고 bin width가 넓어질수록 대략적인 distribution을 추정하게 된다. 반대로 bin width가 좁아지게되면 점점 정확하게 distribution을 추정하게 되는 것이다. 그러나 너무 좁아지게 되고 sample이 충분하지 않게 되면 density estimation의 결과는 좋지 못할 것이다.

위의 식에서 sample의 개수인 $N$ 과 bin width인 $\Delta _i$ 를 observation의 수에서 동시에 나눠주는 이유는 probability를 만들어주기 위해서이다. 여기서 green curve는 우리가 모델링하고자 하는 진짜 distribtuion이고, dataset의 density에 관해서 어떠한 prior knowledge도 존재하지 않는다. 그래서 우리는 여기에 naive한 방식의 density estimation인 histogram을 사용할 것이고, bin width의 크기를 바꿔가며 green curve에 근사시키고자 한다. Histogram에서 bin width와 observation의 수는 정말 중요하다. 그래서 우리는 얼마나 많은 sample을 가지는지에 따라 적절한 bin width를 선택해야 한다.

위의 그림에서 bin width가 작은 경우에는 data의 density를 modeling하는데 있어 더욱 정확한 histogram을 가지고 있다는 의미가 된다. 하지만 만약 각 bin이 가지고 있는 observation의 수가 너무 적어지게 되면 bin width가 작은 bin의 경우에는 아무것도 하지 못하게 된다. Bin width가 넓은 경우에는 green line을 적절하게 추정하지 못하게 된다. 그렇기 때문에 data의 sample 수에 따라 적절한 size를 선택해주는 것이 정말로 중요하다.

Binomial distribution

지금부터는 statistical model을 사용하여 histogram에 대해 생각해보고자 한다. 하지만 우리의 density가 특정한 distribution을 따른다고 가정하지는 않을 것이다. 그렇다고 이를 고려하지 않을 것은 아니고 우리는 각 bin에 statistical model을 적용할 것이다. 새로운 sample이 생겼을 때 이 sample이 특정 bin에 해당하는 경우를 가지고 0이나 1로 나타낼 수 있다. 그렇다면 이러한 binary outcome을 어떻게 modeling할 수 있을까? 우리는 이를 binomial distribtuion을 사용해서 할 수가 있고, 결국 총 $N$ 개의 sample들 중에서 $k$ 개의 sample이 $i$ 번째 bin에 도달할 확률을 modeling 할 것이다. 그리고 이것은 정확히 binomial distribution의 정의를 따른다.

Binomial distribution의 대표적인 예시로 동전을 던져서 앞면이 나오는 확률에 대한 distribution의 모양을 생각하면 위와 같이 종 모양을 형성하게 된다.

2. Kernel Density Estimation(non-parametric)

이제는 위에서 본 binomial distribution을 사용해서 density estimation을 하고자 한다. Non-parametric density estimation으로 histogram을 보았는데, 이번에는 kernel density estimation에 대해서 알아보려고 한다. Histogram의 경우 bin 경계의 불연속성 등 여러 문제점을 가지게 된다. 이 문제점을 kernel function을 이용해서 해결하고자 kernel density estimation 방법이 제안되었다.

여기서 kernel은 window function이라고 생각하면 된다. 보통 data mining에서 kernel은 similarity를 측정할 때 사용하곤 한다. Window function이라는 것은 결국 특정 범위 내에 있으면 동일하다고 생각하겠다는 것이다. 그래서 kernel은 사실상 similarity를 측정하는 것이고, similarity는 결국에는 distance와 밀접한 관련이 있기 때문에 kernel 또한 distance와 관련이 있다고 이야기하는 것이다. 만약 simlilarity를 측정한다고 했을 때, bin을 정의하기 위해서 아마도 kernel을 사용할지도 모른다. 즉, 여기서 kernel이 histogram의 bin을 정의하는 것이다.

먼저 $P$ 를 반지름이 $R$ 인 원 안에 존재하게 될 sample의 probability라고 정의할 것이다. 1차원에서의 range가 2차원, 3차원과 같이 점점 증가해서 n차원이 된다고 했을 때 $R$ 은 이에 대응되는 volume을 나타낼 것이다. 어떠한 공간이 존재한다고 했을 때, 여기에 우리의 data를 던지게 된다면 얼마나 많은 data point들이 특정 bin에 도달하게 될 것인가를 결국에는 $P$ 를 이용해서 설명하겠다는 것이다. 여기서 필요한 것은 $d$ 차원의 space에서 $N$ 개의 data point가 주어졌을 때 $p(x)$ 를 추정하는 것이다.

그래서 $P$ 는 특정 range 혹은 region $R$ 에 대해서 $x$ 의 probability에 대하여 integral을 취한 것이다. Binomial distribution을 사용해서 만약 $N$ 개의 sample과 해당 bin에 존재할 확률인 $P$ 가 주어졌을 때 $K$ 개의 sample이 해당 bin에 존재하게 되는 연속적이 확률들을 나타내고자 한다. 이는 binomial distribution을 따르게 되고 위의 식은 region $R$ 에 도달하게 되는 $K$ 개의 data point들에 대한 distribution을 정의한 것이다.

만약 $N$ 이 점점 커지게 된다면 결국에 $K$ 는 $NP$ 에 근사하게 될 것이다. 이는 "law of large number" 때문이다. $N$ 이 커지게 되면 결국에는 expecation이 의미가 없어지게 되기 때문에 $K$ 가 $NP$ 에 근사하게 되는 것이다. 이러한 상황은 각 bin에 대해서 충분한 sample이 있는 경우에 해당하는 이야기다.
만약 $R$ 을 충분히 작다고 가정하게 되면 그래프 상에서 $R$ 이라는 range에 대한 $p(x)$ 가 아무리 curve 모양을 보이더라도 이를 flat하다고 근사시키게 된다. 이는 말이 어려울 뿐이지 적분을 처음 배울 때 여러개의 사각형들로 intergral 값에 근사시키는 것과 같은 것이다. 이 상황이 되면 $p(x)$ 가 uniform하게 되고 $R$ 에 independant하게 되어 $P$ 는 결국에 uniform한 $p(x)$ 와 volume $V$ 를 곱한 것과 같아지게 된다. 여기서 $V$ 는 차원에 따라 $R^n$ 이 될 것이다.

위의 2가지 내용이 density estimation을 하는데 있어서 중요한 내용들이다. 이 property들을 이용해서 $p(x)$ 를 $\frac{K}{NV}$ 로 추정할 수 있다. 지금까지의 내용들을 통해서 많은 bin들 중에서 우리는 오로지 해당 sample이 특정 bin에 도달할 확률을 modeling 했을 뿐이다. 그리고 이는 binomial distribution에 의해서 modeling 되었고, $K$ 가 $NP$ 에 근사하고 P가 $p(x)V$ 에 된다는 사실을 이야기했다.

지금부터는 binomial distribution을 사용한 estimated probability $p(x)$ 와 histogram의 probability인 $p_i$ 를 비교해보고자 한다.

p(x)=\frac{K}{NV} \qquad \text{vs.} \qquad p_i=\frac{n_i}{N\Delta_i}

Histogram의 경우 해당 bin에서의 probability는 observation의 개수를 총 sample 개수와 bin size로 나눠준 결과가 되었고, 총 $N$ 개의 sample들 중에서 $K$ 개의 sample이 해당 bin에 도달할 확률의 경우에는 $N$ 과 $V$ 를 $K$ 로부터 나눠줄 수 있었다. 이러한 결과를 비교해보았을 때 결국에는 bin size가 region $R$ 의 volume이 되는 것을 알 수 있다. 특정 bin에 대하여 kernel density estimation은 정확하게 histogram의 probability 정의를 따르게 된다. 만약 $N$ 이 크고 $R$ 이 작다면 특정 위치에서의 density를 추정할 수 있는 것이다.

그렇다면 이제는 entire space에 대해서 알아볼 것이고, 이를 위해서는 위에서 region $R$ 에다가 어떠한 행위를 해야할 것이다. 우리는 kernel을 이용해서 $R$ 을 정의할 수 있고, 가장 흔한 kernel로는 다음과 같이 Parzen window를 사용한다.
Parzen window는 hypercube를 통해서 kernel function을 나타낸 것이다. 1차원에서는 bin, 2차원에서는 square, 3차원에서는 cube라고 하면 더 고차원에서는 이를 hypercube라고 부르게 된다. 그래서 우리는 특정 region을 정의하는데, 일반적으로는 $n$ 차원에서 square 형태로 정의하게 된다. 그리하여 Parzen window는 위와 같이 0이나 1로 정의하게 되고, 해당 region 안에 존재하면 1 아니면 0으로 나타내는 것이다. 기준이 항상 원점이 될 필요는 없고 그래서 특정 위치인 $u'$ 를 기준으로 region의 범위를 생각할 수가 있다. 우리는 특정 영역에 존재하는 sample의 개수를 세는 것이고, domain x에 대해서 이를 중심으로 hypercube 안에 몇개의 sample이 있는지 확인하는 것이다.

Sample 몇 개를 그냥 보내야 하는지는 위의 $K$ 를 정의한 식을 보면 된다. 현재 특정 위치인 $x$ 에 대하여 이 위치로부터 우리의 data sample $x_i$ 를 생각해볼 것이고, $x$ 로부터 1/2씩 양 방향 혹은 차원 수에 맞게 window function 혹은 kernel을 가지고 있을 것이다. 총 $N$ 개의 data sample $x_i$ 중에서 일부분은 kernel 범위 안에 존재할 것이고, 나머지는 범위 밖에 존재하게 될 것이다. 모든 sample들에 대해서 $x$ 로부터 멀리 떨어지지 않은 sample들은 radius 안에 존재할 것이고, 이는 미리 정의된 $k(u)$ 에 따라서 1의 값을 가지게 될 것이다. 전체 sample들에 대하여 kernel을 통해서 얼마나 많은 sample이 특정 위치 주변에 있는지 셀 수가 있다. 여기서 $h$ 는 kernel의 bandwidth로, 우리가 좁은 window를 보고 있는지 넓은 window를 보고 있는지 조절할 수가 있다. 결국, $K$ 는 그저 특정 위치 주변에 얼마나 많은 sample이 존재하는지 세는 역할을 하게 된다.

그리고 이렇게 구한 $K$ 를 $NV$ 로 나눠주게 되면 $p(x)$ 가 되는 것이다. $N$ 은 주어지게 되고, $V$ 는 $h^d$ 에 의해서 결정이 된다. $h$ 는 bandwidth로 bin의 size이고 $V$ 는 bin의 volume이다. 그렇기 때문에 $h^d$ 가 되는 것이다. 따라서 최종적으로 $p(x)$ 는 위의 마지막 식과 같이 정의가 된다.

Summary of Density Estimation

Histogram부터 kernel density estimation까지 논리적인 흐름으로 진행이 된다. Binomial distribution을 이용한 kernel density estimation은 대수적으로나 통계적으로나 놀라운 흐름을 보여주었다. 지금까지 봤던 예시와 또 다른 예시를 함께 보도록 하자.
좌측의 예시는 이전에 봤던 histogram의 예시이고 우측의 예시는 kernel density estimation의 새로운 예시이다. $\Delta$ 가 bin width 였다면, $h$ 는 hyper cube size이다. Hypercube의 bin size가 작은 경우에는 green curve에 적절하게 근사하지 못한다. 만약 여기서도 적절한 $h$ 를 찾게 된다면, green curve에 적절하게 근사시킬 수가 있다. 반대로 $h$ 가 너무 크게 되면 결과적으로 너무 smooth해지게 된다. 이렇게 되면 해당 bin size가 model에 적합하지 않게 되어 green line에 근사하지 못하게 된다.

JAEYOON SIM

평범한 공대생의 일상 (글을 잘 못 쓰는 사람이라 열심히 쓰려고 노력 중입니다^^)