[데이터마이닝] Similarity and Dissimilarity - Information Based Measures

JAEYOON SIM·2022년 3월 22일

Data Mining

목록 보기

7/23

Information Based Measures

Information measure에 대해서 알아보기 전에 간단하게 entropy를 이해해야 한다. Entropy에 대해서 설명하면 오늘 밖에 비가 올지 안올지와 같은 불확실한 상황에 대한 uncertainty를 설명하는 척도이다. 그리고 이러한 entropy는 다양한 방법으로 측정될 수 있다. 이러한 과정 속에서 information theory가 등장하였고, 이는 information의 손실을 어떻게하면 최소한으로 줄일지에 대한 이론들이다. 예를 들어 전화기를 통해서 송신자의 전파를 받아 수신자에게 전달한다고 했을 때 중간에서 information의 손실이 발생할 것이다. 물론 중간에 손실이 하나도 없으면 완벽하겠지만, 어디서든 발생할 수 있는 상황이기에 이러한 손실을 최소한으로 줄이고자 했다.

대부분의 similarity measure들은 information theory를 기반으로 한다. 예를 들어 mutual information과 같은 것이 information theory를 기반으로 한다. 그리고 이러한 mutual information과 같은 것은 non-linear한 관계성을 다룰 수가 있다. 이전에 살펴 본 correlation의 경우에는 linear한 관계만을 다룰 수 있었다. 하지만 mutual information의 경우에는 non-linear한 경우도 다룰 수 있다는 것이다. 그렇기 때문에 다소 복잡해질 수 있으며 계산하는데 오래 걸리는 문제도 생길 수 있다.

Information and Probability

Information은 어떠한 사건으로부터 가능한 결과들과 관련이 있다. 즉, information을 확률적인 관점으로 접근할 수 있다는 이야기다. 메시지를 보내는 것, 동전을 던지는 것, data를 측정하는 것과 같은 모든 것들이 information과 관련이 있다는 것이다. 여기서 중요한 점은 결과가 확실할수록 그 결과가 포함하는 information이 적어지게 된다는 것이다. 반대로 결과가 불확실해지게 되면 그만큼 가지고 있는 information의 양은 많아질 것이다.

예를 들어, 원래 동전이 앞면과 뒷면으로 이루어져 있지만 만약에 동전이 2개의 앞면을 가지게 되면 앞면이 무조건 나올 것이기에 불확실성이 존재하지 않게 된다. 앞면이 무조건 나오는 이 상황은 확실함으로 가득차 있어서 어떠한 information도 포함하고 있지 않다는 이야기다.

그리고 양적인 측면에서 information은 결과의 확률과 관련이 있다. 즉, 결과의 확률이 작을수록 더 많은 information을 제공하게 된다. 그리고 희귀한 information일수록 더 중요하게 여겨질 것이다. 이러한 information을 quantification하여 유용한지 아닌지 판단하는 방법으로 entropy가 사용되게 된다. 그래서 entropy를 uncertainty를 측정할 때 사용한다고 이야기한 것이다.

Entropy

Entropy가 uncertainty를 측정하며 이를 수식으로 살펴보려고 한다. 이를 정의하기 위해서 다음과 같이 몇가지 notation들을 정리해보고자 한다.

\text{a variable (event)} : X

\text{with } n \text{ possible values (outcomes)} : x_1, x_2, \dots, x_n

\text{each outcome having probability} : p_1, p_2, \dots, p_n

이러한 notation들을 기반으로 entropy를 다음과 같이 정의할 수 있다.

\text{the entropy of X} : H(X) = -\sum_{i=1}^n p_i\text{ log}_2p_i

여기서 log의 밑으로 2를 사용한 이유는 각 사건들의 결과가 발생할지 안할지가 관심이 있는 부분이기 때문이다. 그래서 이러한 사건의 발생 유무에 따라 총 $n$ 개의 결과가 가능하게 되는 것이다. 우리는 가능한 모든 사건들로부터 각각 $p_i \text{ log}_2p_i$ 를 구하고자 한다. 날씨와 관련해서 흐린 날이 50%, 맑은 날이 20%, 비오는 날이 30%라고 하면 각각 확률을 넣어 계산한 후에 summation을 해줄 것이다. 그리고 여기 log에 확률을 사용하기 때문에 그 값은 항상 음수가 될 것이다. 그래서 마지막에 앞에 minus를 해줌으로써 우리는 entropy를 최종적으로 계산할 수 있게 된다.

컴퓨터는 모든 data를 0과 1로 표현해서 연산을 하게 된다. 그래서 모든 것이 bit로 표현이 되고, entropy는 information의 손실을 줄이면서 data를 표현하기 위해서는 얼마나 많은 bit가 필요한지를 측정하게 된다. 이것이 entropy가 측정하고자 하는 것이고 그 값은 0과 $\text{log}_2 n$ 사이일 것이다. 위의 예시에서 3개의 경우에 대해서 $\text{log}_2 3==1.7xxx$ 이기 때문에 실제로는 3개의 가능한 결과를 encoding하기 위해서는 2개의 bit까지가 필요하게 될 것이다. 2개의 bit를 통해서 총 4개의 경우를 표현할 수 있고 그렇기 때문에 이는 3개의 결과도 충분히 커버할 수 있게 된다.

Entropy Example

앞면이 나올 확률이 $p$ , 뒷면이 나올 확률이 $q(=1-p)$ 인 동전이 있다고 해보자. 이때 entropy는 다음과 같이 구할 수 있을 것이다.

H=\underbrace{-p\text{ log}_2p}_{head} \, \underbrace{- \,q\text{ log}_2 q}_{tail}

case 1) $p = 0.5, q = 0.5 \rightarrow H=1$ (very uncertain)

만약 우리가 아는 일반적인 동전이라면 앞면의 확률과 뒷면의 확률이 반씩으로 entropy를 계산하면 1이 나올 것이다. Entropy 값이 1이라는 것의 의미는 더이상 아무 일도 발생하지 않을 것이란 것과 동일한 의미이다. Entropy가 1이면 maximum entropy 값으로 이는 uncertainty가 최대치에 도달하여 혼돈의 끝에 도달한 상황이다.

case 2) $p = 1, q = 0 \text{ or } p = 0, q = 1 \rightarrow H = 0$ (no uncertainty)

Entropy가 0이라는 것은 uncertainty가 존재하지 않는다는 것과 같다. 즉, 우리는 앞으로 어떠한 일이 발생할지를 알고 있다는 것이다. $p$ 가 1이라는 것은 항상 앞면이 나온다는 것이고 $q$ 가 1이라는 것은 항상 뒷면이 나온다는 것이기 때문에 우리는 굳이 동전을 던지지 않아도 앞으로의 상황을 미리 알 수가 있다. 확실함으로 가득찬 상황을 entropy를 통해서 수치로 알 수 있는 것이다. 이번에는 sample data에 대한 entropy를 살펴보도록 하자.
이번에는 총 5개의 경우가 존재하기 때문에 maximum entropy는 2.3219이고 이는 bit 3개로 encoding 할 수 있을 것이다. 여기서 알아야 할 내용은 data의 distribution이다. Black hair color가 가장 많이 존재하기 때문에 사실상 data가 동등한 distribution으로 존재하지 않는다. 그렇기 때문에 100명을 기준으로 무작위로 한명을 골라 머리 색을 살펴본다면 아무래도 black이 자주 등장할 가능성이 있다. 각각의 $p$ 가 다르기 때문에 $-p\text{ log}_2p$ 값도 머리 색마다 다를 것이다.

이렇게 구한 최종 entropy가 1.1540이고 이를 maximum entropy인 2.3219와 비교를 해보자. 아무래도 2.3219가 1.1540에 비해서 월등히 큰 것을 알 수 있다. 위의 distribution에 따르면 동일한 비율로 존재하고 있는 것이 아니라서 entropy 값이 maximum entropy와는 다르게 많이 작아서 실제로 이러한 상황에서는 모든 경우를 encoding 하기 위해서 오로지 2개의 bit만 있으면 될 것이다. 만약 지금처럼 5개의 경우가 다른 개수로 분포하는 것이 아닌 동일한 개수로 존재하게 된다면 maximum entropy에 따라 총 3개의 bit가 필요하다. 그렇다면 sample data를 좀 더 생각해보기 위해서 다음과 같은 가정을 해보자.

\text{a number of observations}(m)\text{ of some attribute}(X)

(n) \text{ different possible values}

\text{the number of observation in the } i^{th} \text{ category is } (m_i)

$n$ 개의 가능한 결과들을 $m$ 명의 학생들을 이용해서 entropy를 구하면 다음과 같다.

H(x) = -\sum_{i=1}^n\frac{m_i}{m}\text{ log}_2\frac{m_i}{m}

이 식을 보면 살짝 혼란스러울 수 있지만 data matrix로부터 object와 attribute를 생각해보면 쉽다. Entropy를 구하기 위해서는 data matrix로부터 먼저 probability를 구할 필요가 있고, 이를 이용해서 최종 entropy를 구하면 된다. Discrete한 경우에는 다소 쉬울 수 있지만 continuous data에 대해서는 계산이 살짝 복잡할 수 있다. Continuous한 경우에는 discretization을 해줘야하는데 discretization 기법에 따라서 entropy가 다르게 나타날 것이고, 이로 인하여 계산이 복잡해지게 될 것이다.

Mutual Information

지금까지 알아 본 entropy의 경우에는 하나의 variable에 대해서 구한 것이다. 이번에 알아 볼 mutual information의 경우에는 하나의 variable이 아닌 서로 다른 2개의 variable이 제공하는 information에 관한 것이다. 즉, 하나의 variable이 다른 하나의 variable에 제공하고자 하는 information이다. 이를 식으로 나타내면 다음과 같다.

\text{mutual information } I(X,Y) = H(X) + H(Y) - H(X,Y)

H(X,Y) = -\sum_i\sum_j p_{ij}\text{ log}_2 p_{ij}

H(X,Y) : \text{ joint entropy of } X { and}\; Y

p_{ij} : \text{probability that the } i^{th} \text{ value of } X \text{ and the }j^{th} \text{ value of } Y \text{ occur together}

Mutual information $I(X,Y)$ 는 얼마나 $X$ 가 $Y$ 에게 entropy를 이용해서 제공해주는 information이다. 집합에서 일종의 교집합과 같은 개념으로 mutual information을 각각의 entropy와 joint entropy를 이용해서 구할 수 있다. 여기서 $p_{ij}$ 가 결국에는 $X$ 와 $Y$ 의 joint probability를 설명하고 있는 것이다. 그래서 entropy $H(X),H(Y)$ 는 위에서 봤듯이 각각의 probability를 이용해서 구하면 되고, $H(X,Y)$ 는 서로의 joint probability를 이용해서 구하면 된다. 이렇게 구한 3개의 entropy 식을 이용해서 우리는 mutual information $I(X,Y)$ 를 구하면 된다.

이번에도 마찬가지로 data matrix로부터 단순히 계산하게 되면 discrete variable의 경우에는 쉽게 계산이 가능할 것이다. 단순히 개수를 세서 probability를 구하고 mutual information을 구하면 되기 때문이다. 그러나 continuous attribute의 경우에는 discretization 과정을 거쳐서 계산을 해야한다. Maximum mutual information의 경우 discrete variable에 대해서는 $\text{log}_2(\text{min}(n_X,n_Y))$ 와 같이 구해주면 된다.

위의 예시는 mutual information을 구하는 과정을 보여주고 있으며, student status( $X$ )와 grade( $Y$ )의 조합으로 joint probability를 구해서 entropy를 계산한 것이다. 각각의 entropy와는 다르게 mutual information의 값이 상대적으로 많이 작은 것을 볼 수 있다. 이는 학생의 신분이 학부생이든 대학원생이든 상관없이 학생이 받은 학점의 등급에 대해서 많은 것을 말해주지 않는다는 것을 의미한다. 또한 이렇게 작은 mutual information 값은 학생이 어떠한 학점을 받았는지 상관없이 그 학생이 대학원생인지 학부생인지에 대해서 많은 것을 말해주지 않는다는 의미이기도 하다. Mutual information을 통해서 하나의 variable이 나머지 variable에 얼마나 많은 것을 이야기해주는지 확인할 수 있다. 그리고 이는 probability를 기반으로 한 information theory이기도 하다.

Combining Similarities

General Approach for Combining Similarities

Similarity measure를 선택하는데 있어서 global optimum 값이 존재할까? 아마도 아닐 것이다. Attribute에 따라서 때로는 attribute가 여러가지 다른 유형이지만 전체적인 similarity는 필요할 것이다. Nominal, interval, ratio attribute 등이 섞여서 attribute space를 형성할 수 있다. 이러한 경우에는 아마도 서로 다른 proximity를 적용해야 할지도 모른다. 이러한 경우에는 이를 기반으로 마지막에는 하나의 similarity measure를 찾아내야 한다. 이를 위해서는 결국 여러 similarity measure를 하나로 합쳐야 하고, 그 과정은 다음과 같이 진행된다.

이는 여러 similarity measure를 하나로 합치는 방법 중 하나이다. 먼저 $k$ 번째 attribute에서 similarity를 구하게 될텐데, 이 과정에서 indicator variable $\delta_k$ 를 이용해서 0 아니면 1의 값을 부여하고자 한다. 이 과정에서 asymmetric attribute이고 둘 다 값이 0인 경우나 하나라도 missing value가 존재하면 우리는 indicator를 0으로 설정할 것이다. 그리고 이외의 경우에는 1로 설정할 것이다.
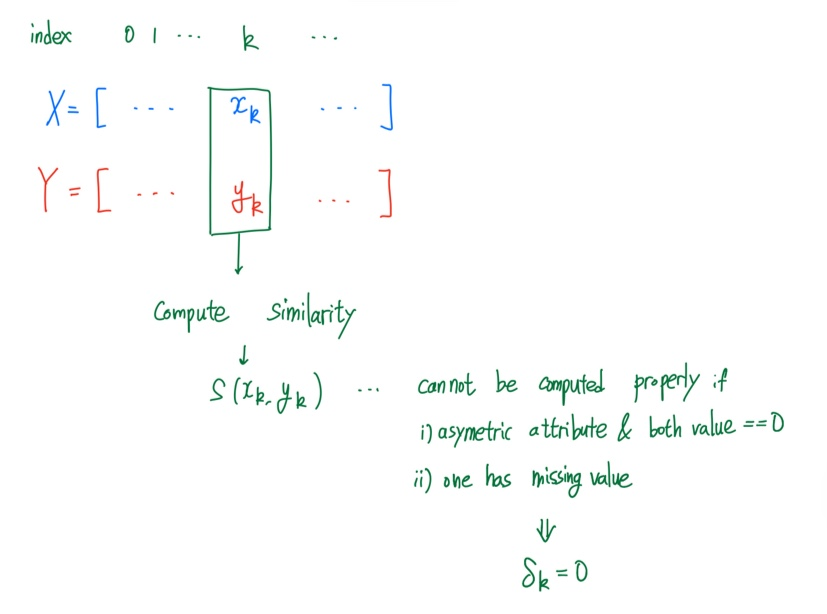여기서 핵심은 만약 우리가 해당 attribute를 포함하고 싶지 않으면 그냥 0으로 설정하면 되는 것이다. 그리고 이를 통해서 총 $k$ 개의 attribute에 대한 전체적인 similarity measure는 다음과 같이 계산하면 된다.

\sum_{k=1}^n \delta_k s_k(X,Y)

만약 $k$ 번째 attribute를 포함시켜야 한다면, 이는 $\delta$ 값을 통해서 결정하면 된다. $k$ 번째 attribute를 포함하게 되면 1을 주기 때문에 전체적으로 동일한 weight를 부여한다고 생각하면 된다. 그리고 이제부터 weight를 다르게 주는 방법에 대해서 알아보려고 한다.

Using Weights to Combine Similarities

모든 attribute가 동일하게 중요한 경우도 있을 것이지만, 그렇지 않은 경우도 종종 있을 것이다. 어떠한 attribute는 상대적으로 덜 중요한 반면에 어떠한 attribute는 상대적으로 더 중요할 수 있는 것이다. 우리는 이를 non-negative weight $\omega_k$ 를 통해서 similarity를 다시 구하고자 한다.

\text{similarity}(x,y) = \frac{\sum_{k=1}^n\omega_k\delta_k s_k(x,y)}{\sum_{k=1}^n\omega_k\delta_k}

$\omega_k$ 는 weight, $\delta_k$ 는 포함시킬지 말지를 결정하는 indicator, 그리고 $s_k(x,y)$ 는 similarity이다. 그래서 similarity를 구하고자 할 때 해당 attribute를 포함할지를 정하고 포함하게 된다면 weight를 부여하는 식의 흐름으로 계산이 된다. 위 식의 분모는 단순히 normalization 때문이고, 이를 통해서 최종적으로 0에서 1 사이의 값을 가지게 된다.