
Feature descriptors
 일반적으로 사진을 보면 모든 영역이 중요한 정보를 가지는 것은 아니다. Key point는 중요한 feature를 가지고 있는데, 이러한 feature를 어떻게 detection할 수 있는지는 이전에 알아보았고 이번에는 찾아진 feature들을 통해서 두 image 사이에서 해당 point들이 서로 대응 관계인지 correspondence를 찾는 방법을 알아볼 것이다. 이러한 correspondence는 feature descriptor를 통해서 찾을 수 있다.
일반적으로 사진을 보면 모든 영역이 중요한 정보를 가지는 것은 아니다. Key point는 중요한 feature를 가지고 있는데, 이러한 feature를 어떻게 detection할 수 있는지는 이전에 알아보았고 이번에는 찾아진 feature들을 통해서 두 image 사이에서 해당 point들이 서로 대응 관계인지 correspondence를 찾는 방법을 알아볼 것이다. 이러한 correspondence는 feature descriptor를 통해서 찾을 수 있다.
Feature descriptor의 목적은 하나의 image patch를 수학적으로 표현하고, 이러한 기술자들을 이용해서 비슷한 patch들을 찾는 것이다. 사람의 눈으로는 다르지만 비슷한 형태를 보이는 것들을 알 수가 있다. 이번에는 이를 수학적으로 어떻게 나타낼 수 있는지 알아볼 것이다.
Detecting feature descriptors
이를 위해서 feature descriptor를 어떻게 디자인할 수 있는지 알아야 한다.
Photometric transformation
 가장 먼저 photometric이란 용어에 대해서 알아볼 것이다. Color, intensity, brightness 등의 변화를 우리는 photometric transformation이라고 한다.
가장 먼저 photometric이란 용어에 대해서 알아볼 것이다. Color, intensity, brightness 등의 변화를 우리는 photometric transformation이라고 한다.
Geometric transformation
 Geometric transformation이라고 하는 것은 영상에서 3D 물체가 움직여서 모양이 바뀌는 것을 말한다. 좌측의 책을 우측과 같이 책상 위에 올려놓는다고 하면 영상에 찍힌 책 표지의 모양이 바뀐 것을 볼 수 있고, 우리는 이를 geometric transformation이라고 한다. 물체가 서로 다른 scale 등 기하학적인 변화를 보여주는 것을 말한다. 그렇다면 image를 설명하고자 할 때 가장 좋은 수학적인 표현 방법은 무엇일까?
Geometric transformation이라고 하는 것은 영상에서 3D 물체가 움직여서 모양이 바뀌는 것을 말한다. 좌측의 책을 우측과 같이 책상 위에 올려놓는다고 하면 영상에 찍힌 책 표지의 모양이 바뀐 것을 볼 수 있고, 우리는 이를 geometric transformation이라고 한다. 물체가 서로 다른 scale 등 기하학적인 변화를 보여주는 것을 말한다. 그렇다면 image를 설명하고자 할 때 가장 좋은 수학적인 표현 방법은 무엇일까?
Image patch
 첫번째로 가장 간단한 방법은 하나의 patch가 주어졌을 때, 거기에 있는 pixel 값들을 바로 사용하는 것이다. Pixel 값들은 전부 intensity value로서 위와 같이 patch가 주어졌을 때 이를 descriptor vector로 표현하기 위해서 intensity value를 순서대로 나열해서 list를 만들 수 있다. 그러면 이러한 vector는 한 patch가 좌측 상단에서 우측 하단으로 가는 순서로 배치가 되었다는 것을 설명할 수 있게 된다. 그래서 우리는 이를 intensity description vector라고 부를 수 있다. 이러한 patch는 비슷한 patch를 만나게 되면 서로 vector간 distance를 구해서 차이가 얼마나 나는지를 보면서 비슷한 patch인지 아닌지를 판단할 수 있게 된다. 이렇게 사용하는 방식이 굉장히 편리한 방식에 해당한다.
첫번째로 가장 간단한 방법은 하나의 patch가 주어졌을 때, 거기에 있는 pixel 값들을 바로 사용하는 것이다. Pixel 값들은 전부 intensity value로서 위와 같이 patch가 주어졌을 때 이를 descriptor vector로 표현하기 위해서 intensity value를 순서대로 나열해서 list를 만들 수 있다. 그러면 이러한 vector는 한 patch가 좌측 상단에서 우측 하단으로 가는 순서로 배치가 되었다는 것을 설명할 수 있게 된다. 그래서 우리는 이를 intensity description vector라고 부를 수 있다. 이러한 patch는 비슷한 patch를 만나게 되면 서로 vector간 distance를 구해서 차이가 얼마나 나는지를 보면서 비슷한 patch인지 아닌지를 판단할 수 있게 된다. 이렇게 사용하는 방식이 굉장히 편리한 방식에 해당한다.
하지만 이러한 식의 patch는 geometry나 물체 겉의 형태 등의 변화 등이 없는 경우에는 괜찮지만 그렇지 못한 경우에는 사용하기 어렵다. 그래서 image patch는 static object라고 해서 움직이지 않는 물체에 대해서 비교할 때 용이하고, 우리는 이를 template matching이라고 부른다. 만약 조명이 꺼져서 전체적으로 영상이 어두워지거나 반대로 밝아지게 되는 상황이라면 intensity value의 변화가 발생할 것이다. 이렇게 모양은 그대로지만 절대적인 값의 변화가 발생할 때에도 image patch를 사용하기 어려울 것이다. 이렇게 image patch를 intensity value로 간단하게 나타내면 생각보다 많은 문제가 발생하게 된다.
Image gradients
 그래서 색이나 밝기가 변할 때 물리적으로 대응하는 관계를 찾을 수 있도록 조금 다른 방법을 생각해 볼 수 있다. Intensity value를 그냥 사용하는 것이 아니라 그 차이를 통해서 gradient를 계산해서 사용하는 것이다. 위에서는 간단하게 방향으로의 미분 값을 사용한 것이다. 숫자 2개씩 좌우로 비교하게 되면 총 6개의 변화량 값이 나올 것이고, 이를 순서대로 배치하여 증가하면 , 감소하면 로 vector를 만든 것이다. 이렇게 binary descriptor의 형태로 vector를 사용하게 되면 이웃한 pixel 사이에서 절대적인 intensity value의 차이가 대소 관계만 바뀌지 않는다면 이러한 descriptor는 바뀌지 않을 것이다. 그래서 동일한 물체가 바뀌지 않고 intensity 값만 달라진다고 했을 때에도 사과를 구성하는 이웃하는 pixel의 변화는 유지되기 때문에 동일한 물체로 판단할 수 있는 것이다.
그래서 색이나 밝기가 변할 때 물리적으로 대응하는 관계를 찾을 수 있도록 조금 다른 방법을 생각해 볼 수 있다. Intensity value를 그냥 사용하는 것이 아니라 그 차이를 통해서 gradient를 계산해서 사용하는 것이다. 위에서는 간단하게 방향으로의 미분 값을 사용한 것이다. 숫자 2개씩 좌우로 비교하게 되면 총 6개의 변화량 값이 나올 것이고, 이를 순서대로 배치하여 증가하면 , 감소하면 로 vector를 만든 것이다. 이렇게 binary descriptor의 형태로 vector를 사용하게 되면 이웃한 pixel 사이에서 절대적인 intensity value의 차이가 대소 관계만 바뀌지 않는다면 이러한 descriptor는 바뀌지 않을 것이다. 그래서 동일한 물체가 바뀌지 않고 intensity 값만 달라진다고 했을 때에도 사과를 구성하는 이웃하는 pixel의 변화는 유지되기 때문에 동일한 물체로 판단할 수 있는 것이다.
하지만 이러한 경우에도 문제는 존재한다. 만약 동일한 물체가 있을 때 하나의 물체가 조금 이동하거나 변형되는 경우에는 변화량으로 판단하기 어려울 수 있다.
Color histogram
 가장 간단한 예시로 위와 같이 영상이 회전된 경우를 생각해보려고 한다. Image gradient를 사용하면 돌아간 영상에 대해서 동일하다고 보장할 수 없게 된다. 그래서 gradient 기반의 descriptor로는 rotation과 같은 경우에 대응점을 판단하기가 어려워진다. Rotation이 발생하더라도 둘 사이의 유사도를 잘 측정할 수 있도록 이번에는 color histogram에 대해서 알아볼 것이다.
가장 간단한 예시로 위와 같이 영상이 회전된 경우를 생각해보려고 한다. Image gradient를 사용하면 돌아간 영상에 대해서 동일하다고 보장할 수 없게 된다. 그래서 gradient 기반의 descriptor로는 rotation과 같은 경우에 대응점을 판단하기가 어려워진다. Rotation이 발생하더라도 둘 사이의 유사도를 잘 측정할 수 있도록 이번에는 color histogram에 대해서 알아볼 것이다.
Histogram을 사용하면 돌아가는 rotation과 꾸겨지는 deformation에 대해서 invariant한 표현을 만들 수 있다. 그래서 위와 같이 patch에서 해당 color 값이 얼만큼 들어있는지 histogram으로 만들어 놓고 사용하는 것이 color histogram 방식이다. Color를 구성하는 성분들이 같기 때문에 rotation이 일어나도 color histogram은 동일하게 표현될 것이다. 그래서 color histogram의 장점으로는 scale이나 rotation에 invariant하게 된다.
여기서 주의할 점은 단순히 histogram만 사용한다고해서 scale에 invariant하지 않을 것이다. Patch의 크기가 다른 경우에는 pixel의 개수가 다르기 때문에 histogram이 쌓인 절대값이 달라지게 될 것이다. 그래서 항상 scale invariance까지 고려를 하고자 한다면 normalization을 통해서 pixel의 개수를 동일하게 맞춰야 한다.
 하지만 이러한 color histogram도 문제는 남아있게 된다. 위와 같이 한쪽은 눈만 표현되어 있고, 다른 한쪽은 머리 전체가 표현되어 있어 spatial layout 자체가 다른 경우에는 color만 분석하는 histogram을 사용하기 어려워진다.
하지만 이러한 color histogram도 문제는 남아있게 된다. 위와 같이 한쪽은 눈만 표현되어 있고, 다른 한쪽은 머리 전체가 표현되어 있어 spatial layout 자체가 다른 경우에는 color만 분석하는 histogram을 사용하기 어려워진다.
Spatial histograms
 조금이라도 뚱뚱하고 날씬한 spatial layout의 경우에도 robust하게 비교를 하기 위해서는 공간을 cell 단위로 나눠야 한다. 위의 예시는 크게 으로 image를 나누어 해당 cell마다 color histogram을 쌓은 것이다. Cell 내에서는 translation에 invariant한 특성이 어느정도 존재하기 때문에 조금 이동해도 상관이 없다. 하지만 이러한 방식은 다시 이전의 문제인 rotation에 invariant하지 않게 될 것이다. Rotation이 발생하면 전체적인 spatial histogram의 configuration이 바뀌게 되어 이 역시 문제가 된다.
조금이라도 뚱뚱하고 날씬한 spatial layout의 경우에도 robust하게 비교를 하기 위해서는 공간을 cell 단위로 나눠야 한다. 위의 예시는 크게 으로 image를 나누어 해당 cell마다 color histogram을 쌓은 것이다. Cell 내에서는 translation에 invariant한 특성이 어느정도 존재하기 때문에 조금 이동해도 상관이 없다. 하지만 이러한 방식은 다시 이전의 문제인 rotation에 invariant하지 않게 될 것이다. Rotation이 발생하면 전체적인 spatial histogram의 configuration이 바뀌게 되어 이 역시 문제가 된다.
Orientation normalization
 이전까지 어느정도 deformation을 개선시키고 있었는데 다시 rotation이 문제가 되니까 rotation을 보정시켜주기 위해서 orientation normalization이라는 기법이 등장하게 되었다. 이 방법은 하나의 대표적인 방향성을 찾는 것이 핵심이다. 위와 같은 patch에 대해서 우측이 dominant한 방향으로 정하는 것이다. 이러한 방향은 image gradient를 보고 정하게 된다. 그래서 한쪽으로 치우쳐진 방향을 찾은 뒤에 해당 방향으로 normalization을 해주게 되는 것이다. 좌측의 image에서 산봉우리를 보면 대표적인 방향이 위쪽에서 살짝 우측으로 치우쳐진 것을 볼 수 있다. 그래서 rotation angle 를 얻게 되고, 이를 따로 저장한 다음에 우측 patch를 description하기 전에 좌측의 patch를 돌려서 가 0이 되도록 만들어준다. 그래서 뾰족한 봉우리가 나오는 경우에는 우측과 같이 돌려놓고 비교할 수 있도록 만드는 것이다. 비교할 수 있도록 전부 동일한 상황으로 만들어 놓는 기법을 orientation normalization이라고 한다. 여전히 이러한 기법도 문제는 존재한다.
이전까지 어느정도 deformation을 개선시키고 있었는데 다시 rotation이 문제가 되니까 rotation을 보정시켜주기 위해서 orientation normalization이라는 기법이 등장하게 되었다. 이 방법은 하나의 대표적인 방향성을 찾는 것이 핵심이다. 위와 같은 patch에 대해서 우측이 dominant한 방향으로 정하는 것이다. 이러한 방향은 image gradient를 보고 정하게 된다. 그래서 한쪽으로 치우쳐진 방향을 찾은 뒤에 해당 방향으로 normalization을 해주게 되는 것이다. 좌측의 image에서 산봉우리를 보면 대표적인 방향이 위쪽에서 살짝 우측으로 치우쳐진 것을 볼 수 있다. 그래서 rotation angle 를 얻게 되고, 이를 따로 저장한 다음에 우측 patch를 description하기 전에 좌측의 patch를 돌려서 가 0이 되도록 만들어준다. 그래서 뾰족한 봉우리가 나오는 경우에는 우측과 같이 돌려놓고 비교할 수 있도록 만드는 것이다. 비교할 수 있도록 전부 동일한 상황으로 만들어 놓는 기법을 orientation normalization이라고 한다. 여전히 이러한 기법도 문제는 존재한다.
Feature extraction
 Image 상에서 perturbation이나 noise, deformation, transformation 등이 적용되었다고 하더라도 description에서 invariance가 그대로 유지가 되는 것을 generalization이 좋다고 표현한다. 이는 영상이 변형된다고 하더라도 대응점을 찾을 수 있다는 이야기다.
Image 상에서 perturbation이나 noise, deformation, transformation 등이 적용되었다고 하더라도 description에서 invariance가 그대로 유지가 되는 것을 generalization이 좋다고 표현한다. 이는 영상이 변형된다고 하더라도 대응점을 찾을 수 있다는 이야기다.
그렇지만 이러한 식으로 invariance를 많이 넣게 되면 구분성이 크게 떨어지게 될 것이다. 비슷하다고 생긴 것들이 약간만 돌아가도 똑같다고 하기 때문에 미묘하게 다른 것들을 구분하는데 어려움이 생기게 된다. 그래서 invariance를 추가함에 따라 구분성, 즉 discriminative power가 떨어지게 된다고 표현한다. 결국 generalization power와 discriminative power는 어느정도 trade-off 관계로 존재한다.
1. HOG descriptor
Feature descriptor가 어떻게 디자인 될 수 있는지 그 과정에 대해서 알아보았는데, 그중에서 성공한 대표적인 사례로 HOG descriptor가 있다.
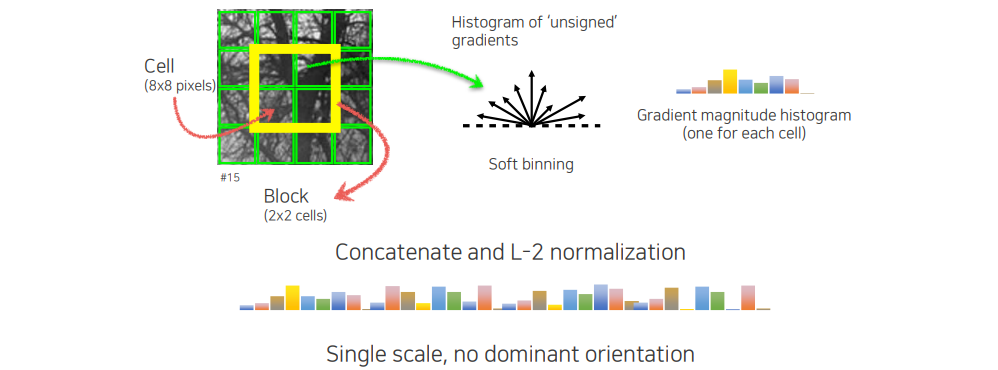 HOG는 histograms of oriented gradients으로 2005년에 제안된 방식이다. HOG를 계산하는 방법은 영상 patch가 먼저 주어지면 이를 cell 단위로 나누게 된다. 이렇게 cell을 나누고 하나의 block을 정해서 이 block으로부터 histogram을 쌓게 된다. 이때는 gradient의 방향을 histogram으로 쌓는 것이고, 여기서 unsigned라고 하는 것은 180도 반대 방향도 동일하게 취급한다는 것을 의미한다. 더불어 각 cell마다 gradient의 크기도 histogram으로 쌓게 된다. 이렇게 쌓은 histogram을 전부 concatenation을 하고 나서 scale에 따라 항상 invariant한 것이 아니기 때문에 normalization을 해줘야 한다. 이러한 식으로 하나의 patch로부터 긴 vector를 만들기 때문에 scale은 하나만 사용하게 된 것이고, 여기서 특별히 orientation normalization과 같은 기법은 사용하지 않았다.
HOG는 histograms of oriented gradients으로 2005년에 제안된 방식이다. HOG를 계산하는 방법은 영상 patch가 먼저 주어지면 이를 cell 단위로 나누게 된다. 이렇게 cell을 나누고 하나의 block을 정해서 이 block으로부터 histogram을 쌓게 된다. 이때는 gradient의 방향을 histogram으로 쌓는 것이고, 여기서 unsigned라고 하는 것은 180도 반대 방향도 동일하게 취급한다는 것을 의미한다. 더불어 각 cell마다 gradient의 크기도 histogram으로 쌓게 된다. 이렇게 쌓은 histogram을 전부 concatenation을 하고 나서 scale에 따라 항상 invariant한 것이 아니기 때문에 normalization을 해줘야 한다. 이러한 식으로 하나의 patch로부터 긴 vector를 만들기 때문에 scale은 하나만 사용하게 된 것이고, 여기서 특별히 orientation normalization과 같은 기법은 사용하지 않았다.
 이러한 HOG는 특히 사람을 찾는 일에 좋은 성능을 보여주었다. 위와 같이 영상 patch가 주어졌을 때 먼저 사람이 존재한다고 가정하고 이를 cell 단위로 나눠준다. 그리고 각 cell마다 oriented histogram을 binning을 해서 쌓아주어 방향성을 나타내도록 한다. 그 결과를 보면 사람이 서 있을 때 vertical 성분들이 많은 것을 통해서 전체적인 경향성을 볼 수가 있다. 이렇게 경향성을 통해서 사람을 쉽게 발견할 수 있기 때문에 HOG를 사람을 찾을 때 주로 사용했다. 이러한 식으로 초창기에는 손으로 디자인해서 사람을 찾는 방법을 만들었다.
이러한 HOG는 특히 사람을 찾는 일에 좋은 성능을 보여주었다. 위와 같이 영상 patch가 주어졌을 때 먼저 사람이 존재한다고 가정하고 이를 cell 단위로 나눠준다. 그리고 각 cell마다 oriented histogram을 binning을 해서 쌓아주어 방향성을 나타내도록 한다. 그 결과를 보면 사람이 서 있을 때 vertical 성분들이 많은 것을 통해서 전체적인 경향성을 볼 수가 있다. 이렇게 경향성을 통해서 사람을 쉽게 발견할 수 있기 때문에 HOG를 사람을 찾을 때 주로 사용했다. 이러한 식으로 초창기에는 손으로 디자인해서 사람을 찾는 방법을 만들었다.
2. SIFT
또 다른 유명한 feature descriptor로는 SIFT가 존재한다. SIFT는 scale invariant feature transform이다.
 SIFT에서는 scale invariance만 중요한 것이 아니라 대부분의 descriptor들이 중요하다. SIFT는 descriptor뿐만이 아니라 앞부분에 key point detector까지 포함하는 하나의 알고리즘에 해당한다.
SIFT에서는 scale invariance만 중요한 것이 아니라 대부분의 descriptor들이 중요하다. SIFT는 descriptor뿐만이 아니라 앞부분에 key point detector까지 포함하는 하나의 알고리즘에 해당한다.
2.1. Multi-scale extrema detection
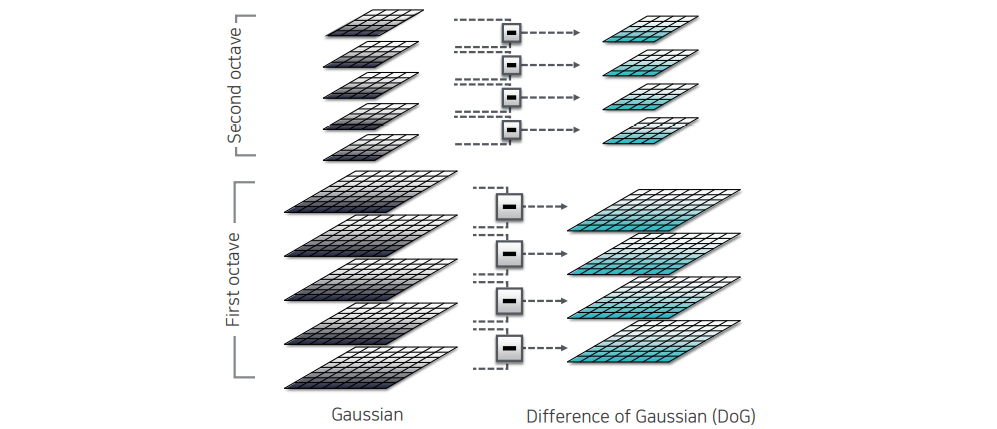 먼저 multi-scale extrema detection의 경우 이전에 multi-scale block을 찾는 방법과 매우 유사하다. 우리가 difference of Gaussian(DoG) pyramid를 사용해서 여러 scale을 보는 것이다. 여기서 octave 개념을 이용해서 정말 작은 image에서도 frequency component를 이용해서 여러 scale을 차등화 하여 좋은 key point가 될 위치를 선정하게 된다.
먼저 multi-scale extrema detection의 경우 이전에 multi-scale block을 찾는 방법과 매우 유사하다. 우리가 difference of Gaussian(DoG) pyramid를 사용해서 여러 scale을 보는 것이다. 여기서 octave 개념을 이용해서 정말 작은 image에서도 frequency component를 이용해서 여러 scale을 차등화 하여 좋은 key point가 될 위치를 선정하게 된다.
 Gaussian과 Laplacian을 비교하게 되면 Laplacian image는 frequency component들만 남긴 것을 볼 수 있고, Gaussian image에서 low frequency는 대략적인 정보를 남기고 high frequency는 디테일한 정보를 남기는 것을 확인할 수 있다.
Gaussian과 Laplacian을 비교하게 되면 Laplacian image는 frequency component들만 남긴 것을 볼 수 있고, Gaussian image에서 low frequency는 대략적인 정보를 남기고 high frequency는 디테일한 정보를 남기는 것을 확인할 수 있다.
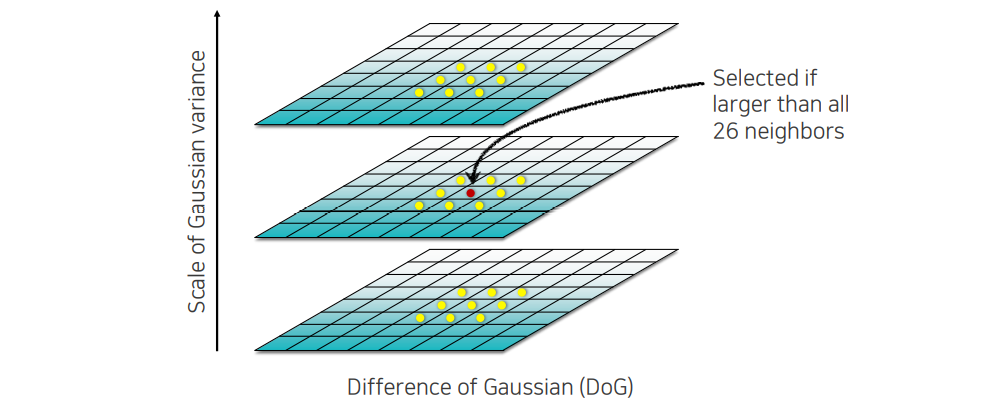 DoG를 이용해서 위와 같이 map을 만들면 주변과 차이가 나는 blob들을 잘 찾게 된다. 그래서 우리가 찾고자 하는 것은 영상이 blur한 영역 내에서 주변의 어떠한 값보다도 큰 값을 가지는 영역을 찾고싶은 것이고, 우리는 이를 extrema라고 한다. 이러한 extrema는 여러 곳에 존재할 것이고, 이를 통해서 중요한 key point가 어디있는지 찾을 수가 있다.
DoG를 이용해서 위와 같이 map을 만들면 주변과 차이가 나는 blob들을 잘 찾게 된다. 그래서 우리가 찾고자 하는 것은 영상이 blur한 영역 내에서 주변의 어떠한 값보다도 큰 값을 가지는 영역을 찾고싶은 것이고, 우리는 이를 extrema라고 한다. 이러한 extrema는 여러 곳에 존재할 것이고, 이를 통해서 중요한 key point가 어디있는지 찾을 수가 있다.
2.2. Keypoint localization
 이러한 선택을 할 때 정수값 단위로만 선택하는 것이 아니라 먼저 훑으면서 search를 하게 된다. 그 다음에 extrema point들을 정수 형태로 찾게 된다. 그러면 이 상태에서 다음 step으로 keypoint localization을 하게 된다. Localization은 정수 위치만 찾는 것이 아니라 소수 위치까지 더 정교하게 찾는 것을 말한다. 이를 위해서 유사하게 이전에는 Taylor approximation을 통해서 주변을 근사하여 극점을 찾았었다. 이번에는 2nd order Taylor series approximation을 통해서 위와 같이 quadratic form으로 주변을 modeling하게 해준다. 그리고 극점을 찾기 위해서 미분해서 0이 되는 지점을 찾아줘야 하고, 여기서 소수 형태를 가지는 extrema point를 얻을 수 있게 된다. 이렇게 얻은 point를 기반으로 주변과 비교해서 strong feature인지 다시 한번 중요한 부분을 filtering 해주는 과정을 수행해주게 된다.
이러한 선택을 할 때 정수값 단위로만 선택하는 것이 아니라 먼저 훑으면서 search를 하게 된다. 그 다음에 extrema point들을 정수 형태로 찾게 된다. 그러면 이 상태에서 다음 step으로 keypoint localization을 하게 된다. Localization은 정수 위치만 찾는 것이 아니라 소수 위치까지 더 정교하게 찾는 것을 말한다. 이를 위해서 유사하게 이전에는 Taylor approximation을 통해서 주변을 근사하여 극점을 찾았었다. 이번에는 2nd order Taylor series approximation을 통해서 위와 같이 quadratic form으로 주변을 modeling하게 해준다. 그리고 극점을 찾기 위해서 미분해서 0이 되는 지점을 찾아줘야 하고, 여기서 소수 형태를 가지는 extrema point를 얻을 수 있게 된다. 이렇게 얻은 point를 기반으로 주변과 비교해서 strong feature인지 다시 한번 중요한 부분을 filtering 해주는 과정을 수행해주게 된다.
2.3. Orientation assignment
 사이에서 key point를 찾아보았는데, 이번에는 orientation에 대해서 dominant한 방향성을 찾고자 한다. Dominant한 방향을 찾아서 기술해 놓고자 하는 것이다. 방향으로 미분해서 제곱해서 루트를 취해주면 이것이 크기가 될 것이고, 의 미분값을 의 미분값으로 나눠주고 arctan을 취해주면 얼마만큼의 비율로 변화했는지 를 구할 수가 있다. 이는 patch에서 하나의 pixel마다 orientation을 구하는 것이고, 이 중에서 가장 dominant한 방향을 찾는 것이다. 가장 dominant한 것은 histogram을 쌓았을 때 peak를 치는 방향을 선택하는 것이다.
사이에서 key point를 찾아보았는데, 이번에는 orientation에 대해서 dominant한 방향성을 찾고자 한다. Dominant한 방향을 찾아서 기술해 놓고자 하는 것이다. 방향으로 미분해서 제곱해서 루트를 취해주면 이것이 크기가 될 것이고, 의 미분값을 의 미분값으로 나눠주고 arctan을 취해주면 얼마만큼의 비율로 변화했는지 를 구할 수가 있다. 이는 patch에서 하나의 pixel마다 orientation을 구하는 것이고, 이 중에서 가장 dominant한 방향을 찾는 것이다. 가장 dominant한 것은 histogram을 쌓았을 때 peak를 치는 방향을 선택하는 것이다.
2.4. Keypoint descriptor
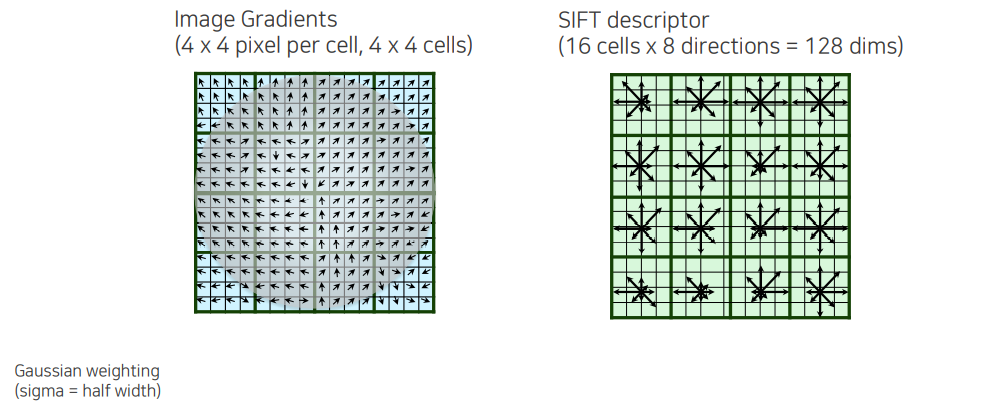 우리는 지금까지 에 해당하는 위치, 에 해당하는 크기, 그리고 에 해당하는 방향까지 찾은 것이다. 해당 위치에서 orientation까지 돌려 놓은 patch를 뜯어 와서 image gradient를 처음으로 구해주는 것이다. 여기서 gradient를 바로 활용하면 너무 민감하다는 문제가 존재한다. 그래서 deformation과 같은 것에 둔감하게 만들기 위해서 spatial cell을 나눠서 spatial histogram을 구성하게 된다. Histogram을 구성할 때 key point 위치 중심에서부터 멀어질수록 덜 중요하다는 Gaussian weighting을 통해서 해당 방향에 대한 gradient의 세기가 얼마인지를 discount 해주게 된다. 우리는 가운에 영역이 더 중요하다고 생각하고자 하는 것이다. 그리고 영역 내에서 Gaussian weight를 통해서 discount된 histogram을 soft하게 쌓아주게 된다. Weight를 통해서 magnitude만큼 더해서 개수로 histogram을 세는 것이 아니라 magnitude에 비례하도록 histogram을 쌓은 형태로 cell들을 만들게 된다. 이렇게 description 된 것을 우리는 SIFT descriptor라고 한다.
우리는 지금까지 에 해당하는 위치, 에 해당하는 크기, 그리고 에 해당하는 방향까지 찾은 것이다. 해당 위치에서 orientation까지 돌려 놓은 patch를 뜯어 와서 image gradient를 처음으로 구해주는 것이다. 여기서 gradient를 바로 활용하면 너무 민감하다는 문제가 존재한다. 그래서 deformation과 같은 것에 둔감하게 만들기 위해서 spatial cell을 나눠서 spatial histogram을 구성하게 된다. Histogram을 구성할 때 key point 위치 중심에서부터 멀어질수록 덜 중요하다는 Gaussian weighting을 통해서 해당 방향에 대한 gradient의 세기가 얼마인지를 discount 해주게 된다. 우리는 가운에 영역이 더 중요하다고 생각하고자 하는 것이다. 그리고 영역 내에서 Gaussian weight를 통해서 discount된 histogram을 soft하게 쌓아주게 된다. Weight를 통해서 magnitude만큼 더해서 개수로 histogram을 세는 것이 아니라 magnitude에 비례하도록 histogram을 쌓은 형태로 cell들을 만들게 된다. 이렇게 description 된 것을 우리는 SIFT descriptor라고 한다.
Other filter basis in histogram feature
SIFT 외에도 filter basis를 사용한 많은 histogram-based feature들이 존재한다.
1D Gabor filter
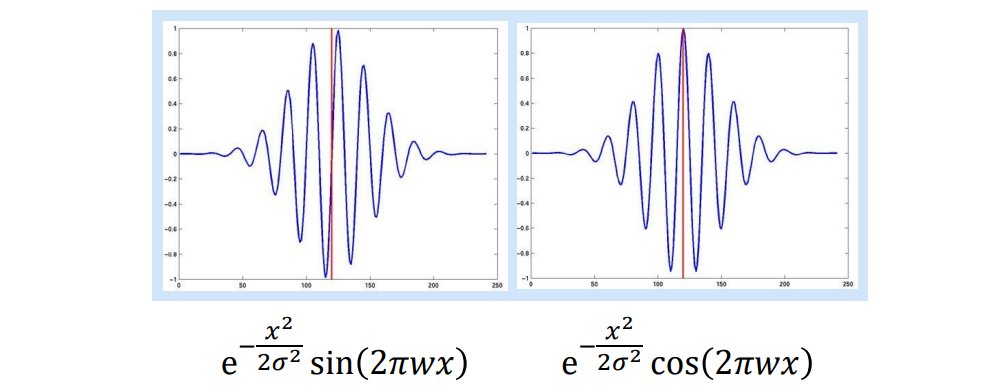 Gabor filter라고 해서 sin과 cos 형태의 filter를 이용해서 filter response를 기록하고, 이를 통해서 특정 영역을 description하게 된다.
Gabor filter라고 해서 sin과 cos 형태의 filter를 이용해서 filter response를 기록하고, 이를 통해서 특정 영역을 description하게 된다.
2D Gabor filter
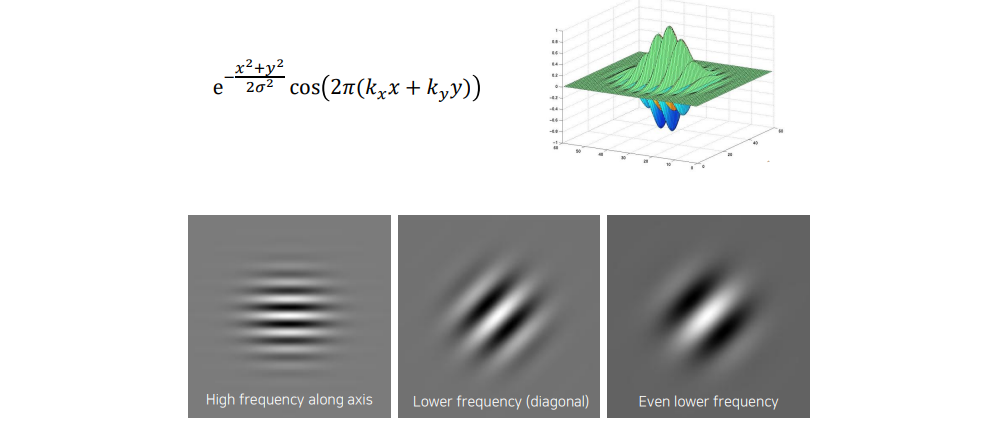 2차원에서는 위와 같이 옆으로 나와 있는 pattern 등을 찾는 detector로 볼 수도 있고, 사선으로 있는 무늬도 찾을 수 있는 detector로도 볼 수 있다. 이러한 filter들이 결국에는 convolution filter로서 사용이 되는데, convolution을 하면 결국 local 영역에 filter와 content 사이의 correlation을 구하게 되고, 여기서 correlation이 큰 값이 나오게 되면 해당 filter와 유사한 정보가 해당 영역에 존재한다는 사실을 알 수가 있다. 그래서 이러한 기술을 통해서 response가 크게 나오는 영역을 찾게되는 것이다. 우리는 서로 다른 resnponse들을 종합해서 image 내에 어떠한 정보들이 있는지 확인할 수가 있다.
2차원에서는 위와 같이 옆으로 나와 있는 pattern 등을 찾는 detector로 볼 수도 있고, 사선으로 있는 무늬도 찾을 수 있는 detector로도 볼 수 있다. 이러한 filter들이 결국에는 convolution filter로서 사용이 되는데, convolution을 하면 결국 local 영역에 filter와 content 사이의 correlation을 구하게 되고, 여기서 correlation이 큰 값이 나오게 되면 해당 filter와 유사한 정보가 해당 영역에 존재한다는 사실을 알 수가 있다. 그래서 이러한 기술을 통해서 response가 크게 나오는 영역을 찾게되는 것이다. 우리는 서로 다른 resnponse들을 종합해서 image 내에 어떠한 정보들이 있는지 확인할 수가 있다.
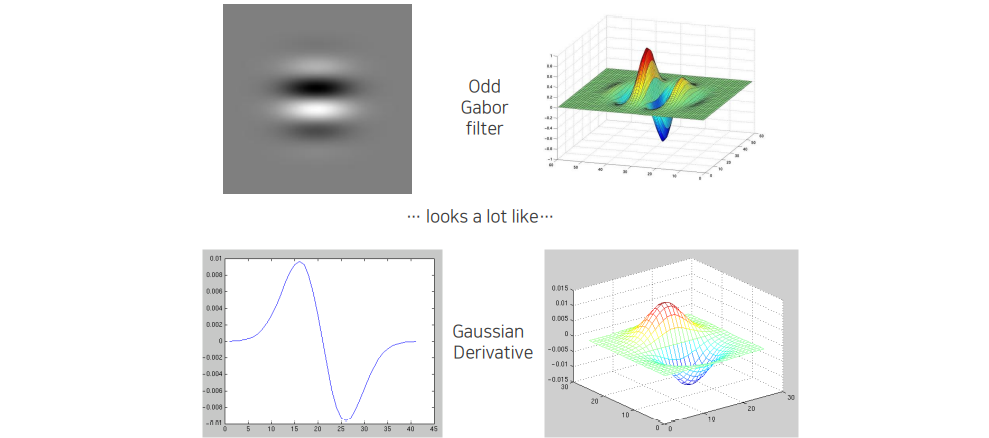 Odd Gabor filter는 중심점을 기준으로 좌우를 빼는 형태로 생겼다. 이는 Gaussian derivative와 비슷한 형태라서 미분을 한 뒤에 Gaussian filter를 취한 형태와 비슷하게 생기게 되었다. 그래서 edge 정보나 edge detection을 하는 것과 denoising이 이미 포함된 filter라고 판단할 수 있다.
Odd Gabor filter는 중심점을 기준으로 좌우를 빼는 형태로 생겼다. 이는 Gaussian derivative와 비슷한 형태라서 미분을 한 뒤에 Gaussian filter를 취한 형태와 비슷하게 생기게 되었다. 그래서 edge 정보나 edge detection을 하는 것과 denoising이 이미 포함된 filter라고 판단할 수 있다.
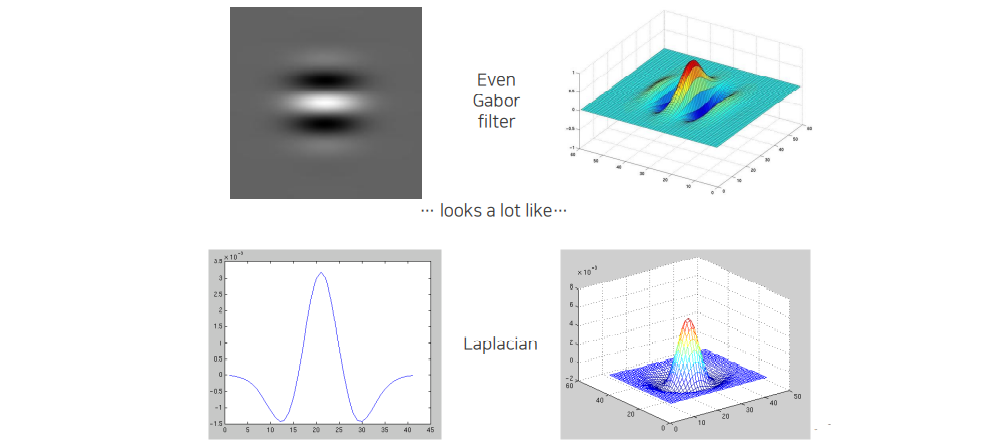 Even Gabor filter는 반대로 Laplacian filter와 형태가 비슷하다. 주변과 대비해서 dominant한 영역을 찾을 수가 있다.
Even Gabor filter는 반대로 Laplacian filter와 형태가 비슷하다. 주변과 대비해서 dominant한 영역을 찾을 수가 있다.
GIST
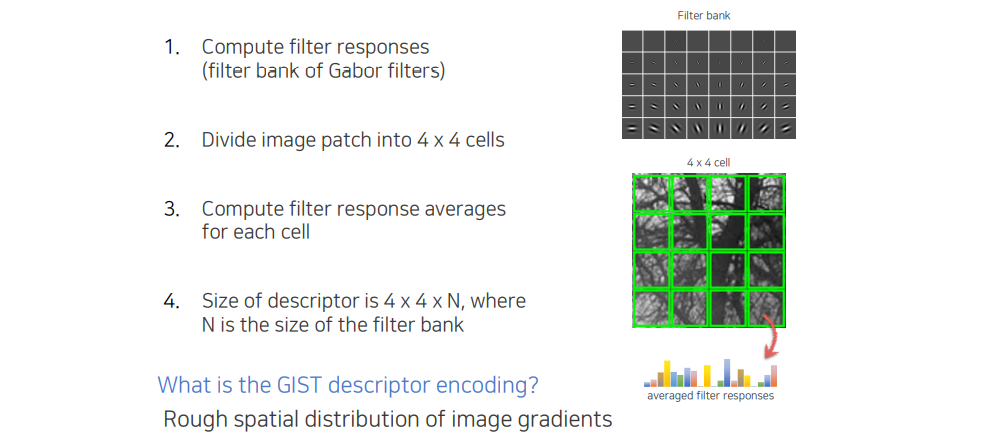 GIST는 Gabor filter를 활용해서 filter response를 종합하는 descriptor이다. 전체적인 구조는 SIFT와 매우 유사하다. 각 cell마다 response들을 histogram을 쌓아서 descriptor를 만들게 된다. 어떠한 방향에 특정 frequency에 들어있는 정보가 얼마나 잘 들어있는지를 포함하고 있다. 영상의 patch보다는 영상 전체의 texture 성분이 얼만큼 들어있는지 판단하기 좋다.
GIST는 Gabor filter를 활용해서 filter response를 종합하는 descriptor이다. 전체적인 구조는 SIFT와 매우 유사하다. 각 cell마다 response들을 histogram을 쌓아서 descriptor를 만들게 된다. 어떠한 방향에 특정 frequency에 들어있는 정보가 얼마나 잘 들어있는지를 포함하고 있다. 영상의 patch보다는 영상 전체의 texture 성분이 얼만큼 들어있는지 판단하기 좋다.
Textons
 이외에도 texture와 같은 정보들을 description할 수 있는 방법들로 Gabor filter와 같이 filter를 사용하는 것이 아니라 texton이라고 해서 특정 texture의 example을 filter 대신 사용해서 해당 texture를 기술하는 방법도 존재한다.
이외에도 texture와 같은 정보들을 description할 수 있는 방법들로 Gabor filter와 같이 filter를 사용하는 것이 아니라 texton이라고 해서 특정 texture의 example을 filter 대신 사용해서 해당 texture를 기술하는 방법도 존재한다.
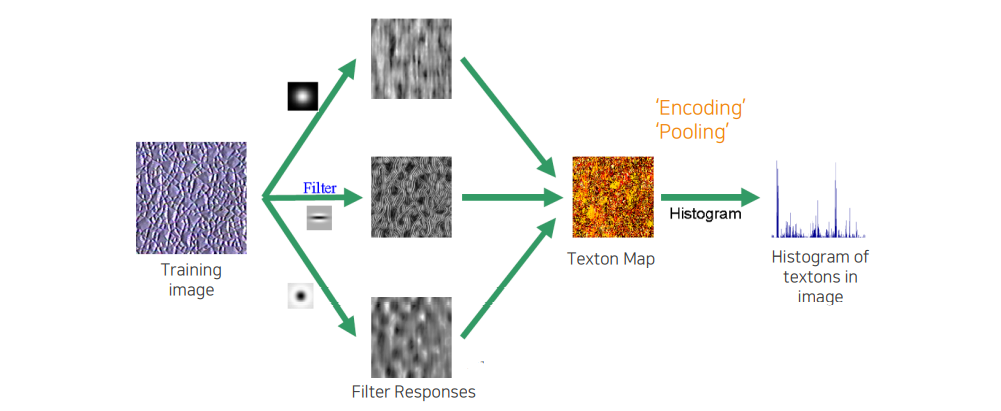 Filtering을 통해서 나온 response들을 잘 종합해서 texton map을 만들게 되고 histogram을 쌓아서 하나의 description vector로 표현하게 된다. 여기서 2D image 형태에서 1D vector 형태로 만드는 것을 우리는 pooling 혹은 encoding이라고 한다.
Filtering을 통해서 나온 response들을 잘 종합해서 texton map을 만들게 되고 histogram을 쌓아서 하나의 description vector로 표현하게 된다. 여기서 2D image 형태에서 1D vector 형태로 만드는 것을 우리는 pooling 혹은 encoding이라고 한다.
