[시각지능] 2D transformations

Image warping

2D transformation을 image domain에서 transformation 관계를 알아보기 위해서 warping에 대해서 먼저 알아야 한다. Image transformation에는 photometric transformation과 geometric transformatin이 존재한다. 여기서 geometric transformation을 warping이라고 하고, domain을 transformation하게 되어 좌표를 변경하게 된다.

Warping example

Key point detection을 통해서 서로 어디에 위치하는지 mapping할 수 있다. 이렇게 matching이 주어졌을 때, 두 image 사이의 관계를 modeling하고자 한다. 이러한 modeling을 통해서 object recognition, 3D reconstruction 등 다양한 application에 사용할 수 있게 된다. 우리는 이렇게 물리적인 관계를 어떻게 계산할 수 있을지 알아보고자 한다.
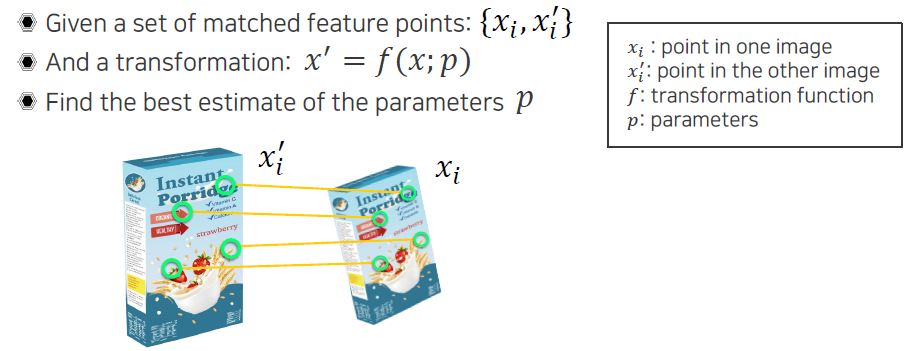이러한 geometric transformation을 얻어내는 방법으로 첫번째는 대응 관계에 해당하는 point의 좌표 set을 모아야 한다. 이러한 point는 key point detection을 통해서 찾으면 된다. 그리고 이렇게 찾은 key point 주변을 key point descriptor를 통해서 표현할 수 있다. 이러한 표현을 통해서 둘 사이의 patch가 얼마나 유사한지 유사도를 계산해서 구할 수 있었다. 유사도를 통해서 유사한 point들을 대응되는 set으로 하여 모은 뒤에는 둘 사이의 관계를 나타내는 $f$라는 function으로 modeling 해야 한다. 이때, $p$라는 unknown parameter로 관계성이 맺어지게 된다. 그러면 우리는 이러한 $p$를 찾아야 하는 것이다. 이를 위해서 $p$를 구성하는 function $f$가 어떻게 정의되는지 알아야 한다.

Panorama from image stitching

Panorama를 구할 때 여러가지 perspective를 보여주면 overlap 되는 부분을 matching 시켜 panorama를 만들게 된다. 이때 어떻게 붙여 넣는지 중요한 관계성을 알아야 한다. 그냥 겹치기만 하면 제대로 된 panorama를 만들 수 없다.
위와 같이 image들이 주어졌을 때 이미 image 사이의 matching 관계들을 알고 있다고 가정해보자. 그러면 이 image들을 translation을 통해서 stitching을 해보고자 한다. 왼쪽을 기준으로 맞는 iamge를 이동시켜 붙이기만 하면 중간에 부자연스러운 균열이 생기는 것을 확인할 수 있다. 우리는 이러한 균열을 seam이라고 한다. 오른쪽을 기준으로 하여도 마찬가지이다.
이를 해결하고자 한다면 이들 사이의 관계를 잘 modeling하는 geometric transformation을 사용해서 붙여나가야 한다. 우리는 이러한 2D geometric transformation을 통칭해서 image homography라고 부른다. Image homography transformation을 통해서 stitching을 하면 더 자연스러운 결과를 만들 수 있게 된다.

View warping

Image transformation을 사용해서 warping을 하면 더 많은 응용이 가능해진다. 위와 같이 복도 사진이 있을 때, 다양한 view로 볼 수 있도록 image를 펼칠 수가 있게 된다. Image를 보면 존재하는 검은 영역은 image를 warping하기 때문에 생기는 영역이다.

Virtual camera rotations

또 다른 응용 사례로는 마치 카메라가 돌아가지 않았는데 옆으로 돌아가서 보는 것처럼 합성된 rotation view를 만들 수가 있다.

Image rectification

그리고 건물을 아래서 촬영했을 때, 건물의 아랫 부분은 넓고 위쪽은 좁게 찍히게 될 것이다. 하지만 image를 warping시키게 되면 마치 image를 정면에서 본 것처럼 펼칠 수가 있다. 이러한 것을 image rectification이라고 하며, 이는 image를 정면에서 본 것처럼 펴주는 역할을 하게 된다. 그래서 image transformation 관계를 알게되면 다양하게 응용이 가능해지게 된다.

Street art

또한 예술적인 범위에서 많이 활용이 된다. 2D transformation 관계를 통해서 착시 현상 등을 만들 수 있다.

2D transformations

이 관계를 나타내는 2D transformation model을 어떻게 생겼는지 이제부터 알아보고자 한다. 2D transformation은 다음과 같이 구분할 수 있다.
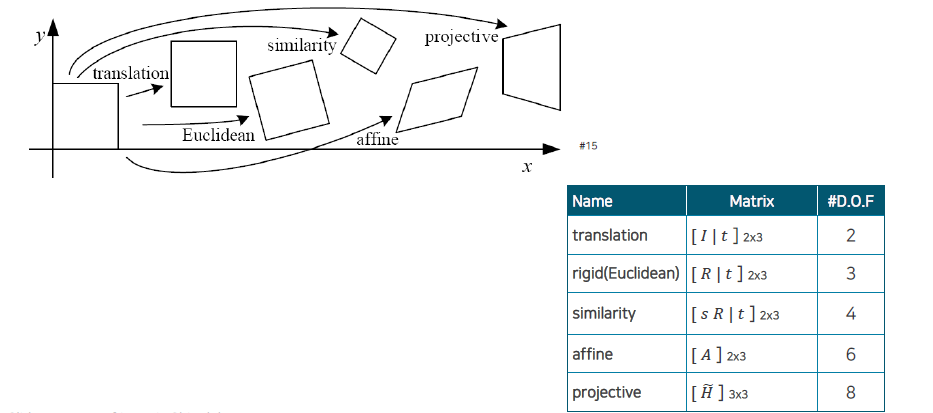Translation부터 projective로 한단계씩 갈 때마다 degree of freedom(DOF)라고 해서 우리가 조정할 수 있는 unknown parameter의 개수가 늘어나게 된다. DOF가 높아질수록 더 다양한 transformation을 표현할 수 있게 된다.
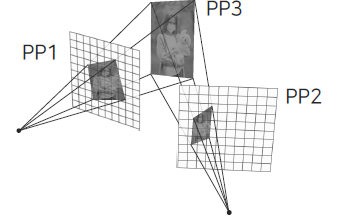이렇게 projective transformation까지가 2D transformation을 전부 포함하고 있는데, 이때 이 관계가 무엇을 나타내는지 알아보고자 한다. 위와 같이 PP3 위치에 사진이 하나 있다고 해보자. 그리고 서로 다른 카메라가 PP1과 PP2에서 PP3의 사진을 바라보고 있다고 해보자. 카메라의 중심으로부터 사진을 바라보았을 때 해당 위치에 따라 image plane에 사진이 다르게 맺히게 될 것이다. 이때, 실제 사진과 image plane에 놓이는 사진 사이의 관계는 projective transformation 관계일 것이다. 두 위치에 존재하는 image plane 위 사진과 실제 사진 사이의 관계가 각각 projective transformation 관계가 된다면, 두 image plane에 놓인 사진 사이의 관계 또한 projective transformation 관계가 될 것이다. 그래서 plane과 plane 사이의 관계는 2D transformation을 사용해서 나타낼 수 있게 되는 것이다. 우리는 이러한 projective transformation을 다른 말로 homography라고 한다.

우리가 다른 transformation을 이용해서 stitching을 해보면 이들이 어떻게 다른지 확인할 수 있다. Projective transformation의 경우 물체의 형태를 최대한 유지를 하면서 stitching을 할 수가 있는 DOF가 높은 transformation임을 확인할 수 있다.

위는 다양한 2D transformation을 보여주고 있는데, 여기서 cylindrical transformation만 제외하고 위에서 살펴보았던 2D transformation을 표현하는 방법으로 전부 표현이 가능하다.

2D planar transformation

지금부터는 2D transformation을 수식적으로 어떻게 표현할 수 있는지 알아보고자 한다. 위와 같이 정사각형이 2D 평면 위에 놓여있다고 해보자.

Scale

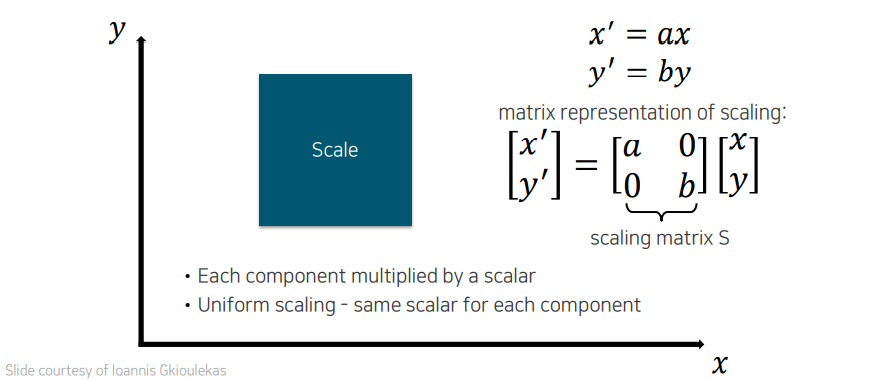가장 먼저 우리는 기존의 정사각형의 크기를 키우고자 한다. 크기를 키우는 것을 어떻게 구현할 수 있을까? 그냥 단순하게 uniform scale을 각 좌표에 곱해주면 된다. $a,b$가 같은 경우에는 aspect ratio가 유지된 상태로 크기가 커지게 될 것이지만, 다른 경우에는 한쪽으로 늘어진 형태로 크기가 달라지게 될 것이다. 이를 깔끔하게 $2\times2$ scaling matrix $S$로 표현할 수 있다.

Shear

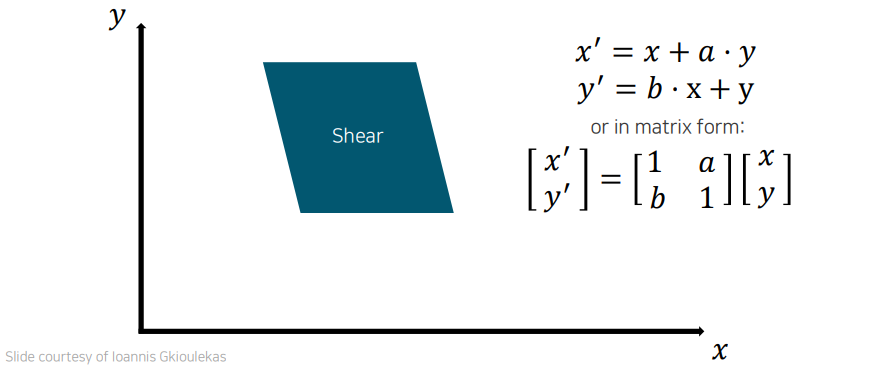이번에는 shear transformation에 대해서 알아보고자 한다. 이는 옆으로 비틀어버리는 것으로 원래의 scale은 변화시키지 않고 $x$와 $y$ 사이에 간섭을 주는 것이다.

Rotation

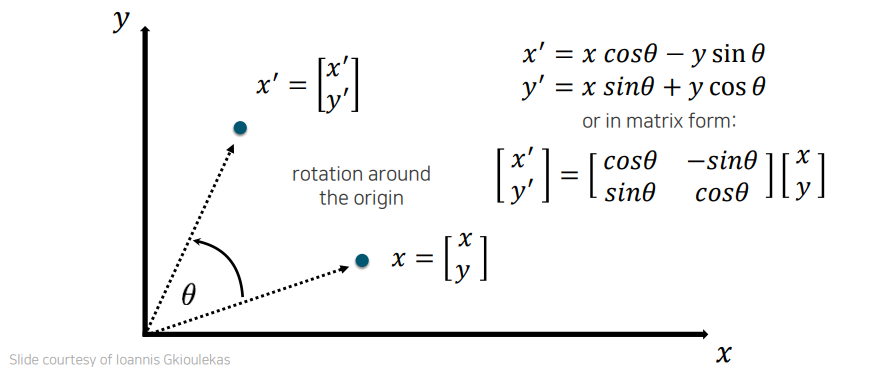Rotation은 $x$에서 $x'$으로 돌리는 수식을 위와 같이 $2\times2$ matrix $R$로 정의하면 된다.
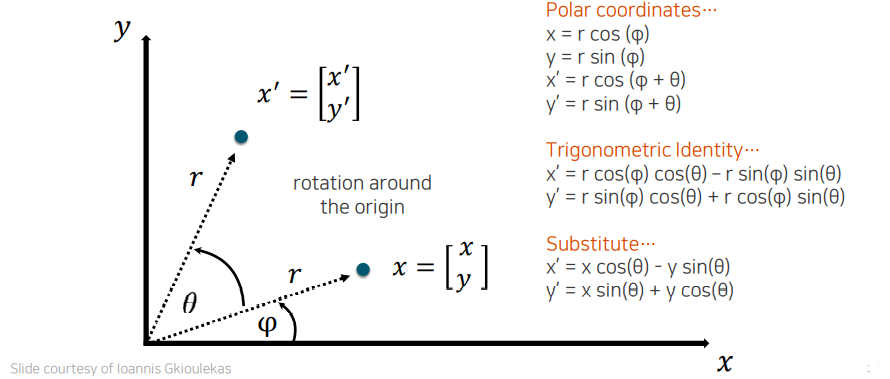이러한 관계식은 polar coordinate로부터 시작해 유도할 수 있다.

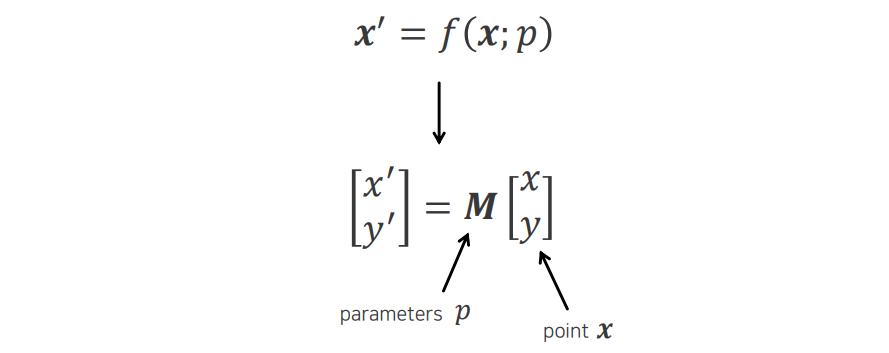지금까지 살펴보았을 때 두 좌표 사이의 function $f$는 간단한 $2\times2$ matrix $M$ 형태로 표현이 가능하다는 것을 알 수 있다. 여기서 unknown parameter $p$는 우리가 어떠한 transformation을 할 것인지에 따라 정의할 수 있다.

어떻게 $M$을 정의하는지에 따라 위와같이 다양한 관계를 표현할 수 있다.

2D translation

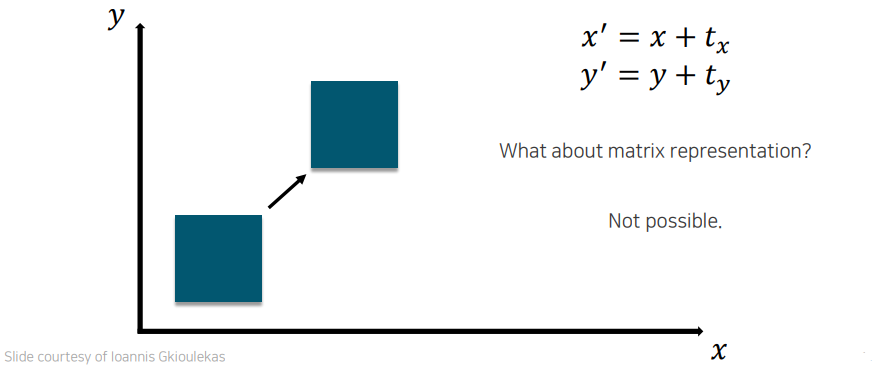이번에 살펴 볼 관계는 2D translation으로 지금까지 설명했던 여러 operation처럼 또 다른 중요한 개념이다. Translation은 위와 같이 각 좌표에 offset을 더해줌으로써 수식적으로 표현이 가능하다. 우리는 이전까지 두 좌표 사이에 $M$을 통해서 표현이 가능했었다. 하지만 translation은 이러한 $M$ 하나만으로 modeling이 되지 않는다. 다음에는 이러한 2D translation을 포함하는 전체적인 2D transformation을 어떻게 표현할 수 있는지 modeling 방법을 살펴볼 것이다.