Image downsampling
만약 상반신이 찍힌 사진을 우리가 화면을 통해서 본다고 했을 때, 사진이 너무 크면 상반신 전부를 한번에 보기 힘들 것이다. 이러한 경우에는 사진의 크기를 줄여서 화면에 담아야만 할 것이다.
Naive image subsampling
이렇게 영상을 줄여야하는 방법 중에서 naive한 방법 중 하나가 바로 row와 column을 한줄씩 날려버리는 것이다. 위와 같이 특정 row와 column을 날려가면서 절반씩 줄여나갈 수 있다. 하지만 이렇게 영상을 반으로 줄여나가다보면 기본적으로 발생하는 문제가 존재한다. 위에서 작은 영상을 보게 되면 그렇게 큰 문제는 없어보인다.
하지만 이를 다시 확대해서 보게 되면 문제가 생겼음을 확인할 수 있다. 크게 줄였다가 다시 확대시킨 영상의 경우에는 기존 원본보다 많은 정보의 손실이 발생했음을 알 수 있다. 자세히보면 pixel들이 뭉쳐 있는 느낌을 받을 수 있고 우리는 이를 pixlated 되었다고 이야기한다. 우리는 이렇게 영상을 줄여나가는 기법을 image subsampling이라고 하는데, 이러한 방법은 원래 영상의 정보를 많이 훼손시키게 된다.
Sampling
먼저 sampling에 대해서 이해해보려고 한다. 위와 같이 sin wave가 있을 때, 이를 영상의 한 축이라고 생각하고 이를 디지털화 시키려고 한다. 공간 축이라고 생각하고 일정 간격으로 그 값을 취득하려고 할 것이다.
그렇게 취득을 하면 위와 같이 data가 일정 간격으로 존재할 것이다. 위의 경우 상당히 많은 data를 얻었기 때문에 대충 그려봐도 sin wave와 유사할 것이다.
Undersampling
이번에는 우리가 sin wave를 undersampling하는 상황을 보고자 한다. 간격을 느슨하게 해서 data를 취득하게 되면 완전 다른 sin wave가 형성이 될 것이다. 이렇게 되면 기존의 정보를 잃게 될 것이다.
그래서 이렇게 적은 수의 sampling을 한 경우에는 낮은 주파수의 sin wave를 얻기에 원래 정보를 왜곡할 수가 있다. 그래서 원래 존재하는 signal과 우리가 취득한 signal을 모르고 있다고 하면 혼란을 일으킬 수 있다.
사실 data를 위와 같이 취득했을 때 반대로 높은 주파수가 될 수도 있는 것이다. 그래서 undersampling을 하게 되면 기존의 정보를 복원해내는 것이 상당히 애매하기 때문에 구분하기가 어려워진다. 그렇다면 만약 우리가 공교롭게도 undersampling으로 data를 취득한 경우에는 어떻게 해석을 해야하는 것일까?
Aliasing
원래 주파수가 있는데 낮은 주파수로 착각을 한다든지 해서 구분을 못하게 되면 discretization 과정에서 이를 aliasing effect라고 한다. 기존 적은 frequency와 원래 frequency에서 둘 사이의 구분성이 undersampling을 통해서 잃었을 때를 aliasing effect라고 하는 것이다.
이러한 aliasing 현상을 image에서 많이 얻을 수 있고, 이를 또한 moire effect라고도 한다. 굉장히 반복적인 패턴이 있을 때, 위와 같은 패턴은 실제로 존재하지 않는다. 촬영하는 카메라의 sensor 배치가 sampling rate하고 일치하게 되는데, sensor의 배치가 실제로 우리가 관찰하는 대상보다 덜 촘촘해서 undersampling이 되어 low frequency의 특성을 측정하는 것과 같아지는 효과가 생겨 우리가 쉽게 착각하게 되는 것이다. 그래서 이러한 패턴은 원래의 signal이 왜곡된 것으로 이해해야 한다. 지금까지 본 이러한 현상은 전부 공간 축에서 형성된 것이다.
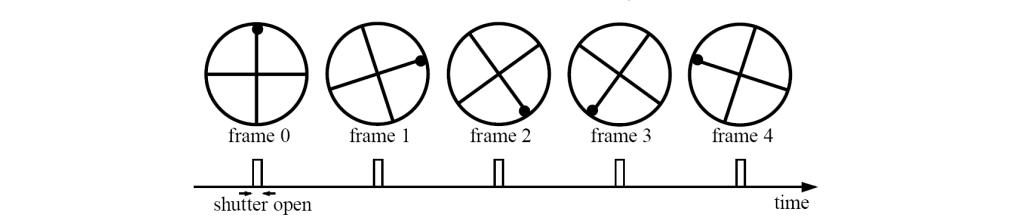공간 축에서 뿐만 아니라 시간 축에서도 aliasing이 발생할 수 있다. 이는 주로 video에서 많이 발생하게 된다. 항상 영상을 취득할 때 공간 축에 대한 aliasing과 시간 축에 대한 aliasing을 함께 고려해야 한다. 우리가 shutter 속도를 조절함으로써 1초에 30, 24 frame 등을 촬영하게 되는데, 이때 shutter를 열고 닫는 것을 일종의 sampling rate라고 볼 수 있다.
이와 다르게 너무 빠른 물체를 느리게 촬영하게 되면 또다시 aliasing이 발생하게 될 것이다. 대표적인 예시로 돌아가는 자동차 바퀴를 생각할 수 있다. 영상을 보면 바퀴가 돌아가고 있는데 너무 빠르다보면 우리가 생각하는 것과 반대로 돌아가는 것처럼 보이게 된다. 바로 이러한 것이 undersampling effect인 것이다.
Anti-aliasing
그렇다면 이러한 aliasing을 어떻게 해결할 수 있을까? 원래 signal로부터 undersampling한 결과를 다시 원래의 signal로 어떻게 복원시킬 수 있을까? 아무래도 undersampling 된 data만으로는 앞서 이야기했듯이 높은 frequency인지 낮은 frequency인지 구분하기가 어렵다. 이러한 이유로 사실 완벽하게 원래 signal을 복원하는 것은 다소 어렵다.
그래도 복원을 하고자 할 때 생각할 수 있는 첫번째 방법으로는 아예 undersampling을 방지하고자 signal을 oversampling 하는 것이다. 또 다른 방법은 signal 자체를 smoothing하는 것이다. 어차피 우리가 추정하지 못하는 high frequency component들은 전부 지워버리는 것이 두번째 방법이다. 그래서 aliasing을 발생시킬 수 있는 high frequency component들을 전부 없애서 undersampling 했을 때 관찰이 가능한 정보들만 남겨 놓는 것이다. 이랬을 때 당연히 정보는 일부 사라지지만, 잘못된 signal이 들어가서 헷갈리는 형태들을 미리 피할 수가 있을 것이다.
이렇게 두가지 방법을 알아보았는데 실제로는 우리가 카메라의 제약 등의 이유로 oversampling을 하지 못하는 경우도 존재할 것이다. 이러한 경우에 software적으로 접근해서 aliasing을 발생시킬 수 있는 부분들을 지우고 사용하자는 것이다. 그렇다면 어떻게하면 signal을 smoothing할 수 있을까? 이는 어떻게 하면 high frequency component들을 지울 수 있을지에 대한 고민으로 이어진다.
Better image downsampling
High frequency component들을 지우기 위해서 먼저 smoothing을 해주는 것이다. 그래서 image를 downsampling할 때 column하고 row를 한번씩 번갈아가면서 지우는 것이 아니라 그 전에 Gaussian filtering을 통해서 먼저 blur를 일으켜 high frequency component를 지우고 짝수 column과 row를 지워 홀수 column과 row만 남겨놓으면 된다.
이렇게 줄인 영상을 다시 키우게 되면 이전보다 형태가 더 잘잡힌 결과를 볼 수 있게 될 것이다. High frequency component들은 잃어버리게 되지만 우리가 중요했던 low frequency에 대한 component들을 유지해서 우리가 영상의 원본을 유추할 수 있는 단계까지 갈 수 있는 것이다.
확실히 기존의 Naive한 downsampling 결과와 비교해보면 더 나은 것을 확인할 수 있을 것이다.
Gaussian image pyramid
우리가 이러한 형태를 연속으로 적용해서 만들게 되면 이를 Guassian image pyramid라고 한다. 원본 image에서부터 점점 줄여가면서 Gaussian image pyramid를 미리 만들어 놓고 여러가지 해상도를 참조를 해서 사용할 수가 있다.
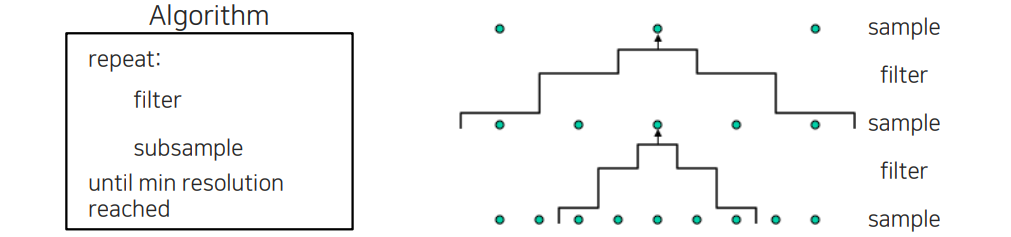Gaussian pyramid를 만드는 방법은 먼저 filtering을 해주고 subsampling을 해주는데, 이를 가장 작은 resolution이 될 때까지 반복하면 된다. 이러한 식으로 downsampling을 하게 되면 그 사이에 있는 영상들은 전부 복원이 되어 pyramid 형태를 보여주게 된다.
Gaussian pyramid가 어떠한 특성을 가지는지 알아보려고 한다. Gaussian pyramid는 디테일한 high frequency부터 low frequency까지 그 정보를 모두 보존할 수 있다. 그래서 높은 layer로 갈수록 smoothed out이 되어 더 blurry해지게 된다.
그렇다면 가장 높은 level의 image는 어떠한 정보를 가지게 될까? 이 image들은 uniform한 영역에 대한 정보들이 보존되어 있다. 위의 예시와 같이 원래 image에 존재하는 얼룩말 무늬들이 가장 높은 level로 가면 갈수록 더 보이지 않게 된다. 그래서 여기에는 low frequency component들만이 모여있게 되는 것이다.
그럼 이렇게 downsampling 된 image들을 이용해서 원래의 image를 복원시킬 수 있을까? 생각을 자세히 하게 되면 이는 실제로 불가능할 것이다. 더 높은 level로 올라갈수록 정보를 잃어버리게 된다. 이렇게 되면 정보의 손실이 있기 때문에 우리는 정보의 손실이 있는 상태에서 거슬러 올라가는 것은 아무래도 원래 signal을 완전히 복원하는 것은 불가능할 것이다.
Laplacian image pyramid
Guassian image pyramid를 통해서 완전히 복원이 불가능하다면 어떻게 할 수 있을까? 우리는 원래 image와 downsampling을 하기 위해서 blurring을 취한 image를 빼보면 residual을 얻게 될 것이다. 그래서 원본 iamge와 blurring한 image 사이에서 발생하는 오차를 얻고, 우리는 실제로 이러한 오차만큼 정보를 잃어버리게 될 것이다. 앞서 발생했던 문제를 다시 생각해보면 우리는 이렇게 잃어버리는 정보들을 이용하여 원래 image를 복원시킬 수 있을 것이다.
그래서 만들어진 개념이 바로 Laplacian image pyramid이다. Gaussian image pyrmaid를 사용하는 경우도 있지만, Laplacian image pyramid를 사용하는 경우도 굉장히 많이 존재한다. 각 level에서 residual 정보만 남겨놓으면 원래의 signal을 복원시킬 수가 있다. 위의 Laplacian image pyramid를 보면 가장 높은 level을 제외하고는 residual 정보를 가지고 있다. 가장 높은 level에서는 intensity 정보를 가지게 된다. 여기서 원래 image를 복원하고자 한다면 가장 높은 level의 image를 upsampling한 다음에 직전 level의 residual 정보를 더해서 해당 level의 결과를 복원하는 것이다. 이러한 식으로 계속해서 복원하다보면 원래 image를 복원할 수 있을 것이다.
우리는 Gaussian과 Laplacian filter에 대해서 이미 알고 있기에 위와 같이 생긴 것을 확인할 수가 있다. 사실 여기서 Laplacian filter를 직접 사용하는 것은 아니다. 대신 원래 image는 delta function을 사용해서 filtering 되었다고 볼 수 있고, 원래 image에서 Gaussain filtering을 했다고 보게 되면, 이 둘을 빼서 Laplacian function과 비슷한 filter response를 얻을 수가 있다. 그래서 이러한 filter를 원래 image에 적용한 것과 비슷한 response의 결과를 얻을 수가 있는 것이다. 위에서도 보면 Gaussian을 빼서 만들어지는 function하고 Laplacian 형태하고 비교를 해보니까 실제로 오차가 거의 없음을 확인할 수 있었다. 그래서 이를 어떻게 보면 Gaussain의 difference가 Laplacian을 approximation한다고 볼 수 있는 것이다.
Other types of pyramids
Gaussian pyramid와 Laplacian pyramid 외에도 다양한 종류의 pyramid들이 존재한다. Image sampling을 여러개 해놓고 복원한 다음에 application을 위해서 사용할 수가 있는데, 이때 사용하는 것 중에 steerable pyramid라는 것이 존재한다. Laplacian pyramid가 원래의 정보를 복원할 수 있는 만큼 다양한 frequency 정보들을 보관하고 있다고 볼 수 있는데, steerable pyramid같은 경우는 원본을 최대한 복원할 수 있도록 filtering을 하고 downsampling을 해서 저장을 하는 방식인데 중요한 차이로는 이를 방향에 따라서 한다는 것이다. 1D signal의 경우 frequency 정보만 있지만 image의 경우에는 방향성도 있어서 각 방향마다 frequency 정보들을 모아서 stterable pyramid를 만들어 정보를 표현하여 원본을 복원시킬 수 있다. Wavelet도 마찬가지로 image들을 high frequency 정보들과 low frequency 정보들로 나눠서 보관해서 사용할 수가 있다.
Image interpolation
Downsampling은 정보를 잃는 과정으로 요약할 수 있다. Image interpolation은 위와 같이 여러 방법들이 존재한다. 그래서 원래의 image가 작을 때 이웃한 pixel들을 여러번 복사해서 image를 만드는 nearest-neighbor interpolation이 있고, 어떤 2개의 sample의 사이값이 직선 위에 있다고 가정하고 사이 값을 sampling하는 bilinear interpolation, 직선이 아니라 곡선 위에서 sampling하는 bicubic interpolation 등이 존재하게 된다.
Image interpolation의 경우 geometric warping이라고 해서 영상을 왜곡시키게 되는 것이다. 영상을 왜곡시키는 transformation을 하게 되는데, 이때 color 값을 결정하는 것은 반대로 가서 확인했을 때 대부분 해당 위치에서 값들이 실수로 존재하게 되는데 주변 color와 거리 비율로 따져서 resampling 해주면 된다.
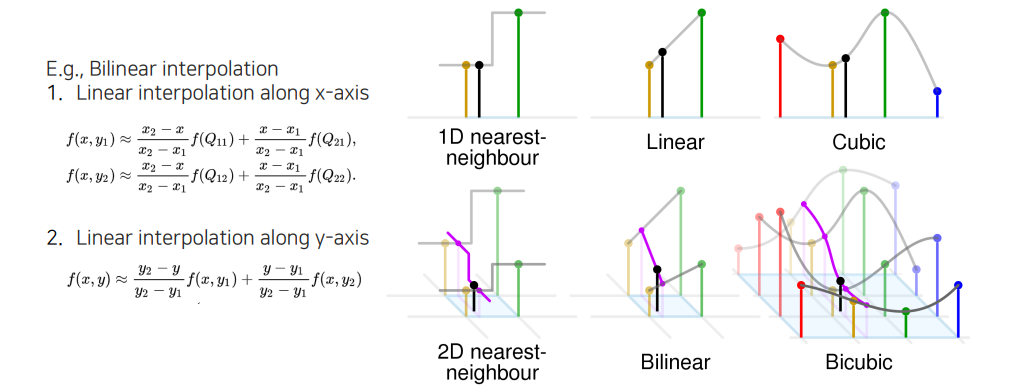다시 이를 자세히 식으로 보면 nearest neighbor의 경우 가장 근접한 값을 사용하는 것이고, linear이나 cubic은 직선과 곡선 등을 fitting해서 이 선들 위에서 color 값을 sampling해서 사용하면 된다.
이외에도 advanced interpolation 방법들이 다수 존재한다. Interpolation이라고 하는 것은 sampling 된 signal을 사이 값을 추정해서 다시 복원하는 것인데, 원본 signal을 다시 복원하는 것은 이미 정보를 잃었기 때문에 어렵다. 하지만 우리가 좋은 화질을 얻고자 한다면 이미 잃은 정보를 복원할 수 있어야 한다.
