Image processing basic
이번에는 image를 어떻게 processing하는지 알아보고자 한다. Image processing이라는 것은 image를 변환하는 것이다. 여기에는 크게 2가지 카테고리가 있다. 하나는 영상의 컨텐츠는 바뀌지 않고 안에 있는 값들이 바뀌면서 영상의 특징이 바뀌는 것이 있고, 다른 하나는 영상의 구조가 바뀌는 것이 있다. 우리는 전자를 image filtering 혹은 photometric transform이라고 하며, 후자를 image warping 혹은 geometric transform이라고 한다.
영상을 filtering할 때 이를 function 형태로 볼 수 있다. 를 pixel, 를 image를 grid level로 봐서 discrete한 function으로 생각할 수 있다. 이때, image filter로서 영상 자체에 적용이 되어 를 만들게 되는 것이다. 반면, Image warping에서는 가 안에 들어온 것을 확인할 수 있다. 가 들어왔을 때 가 참조하는 위치 자체를 먼저 바꿔준 것이다.
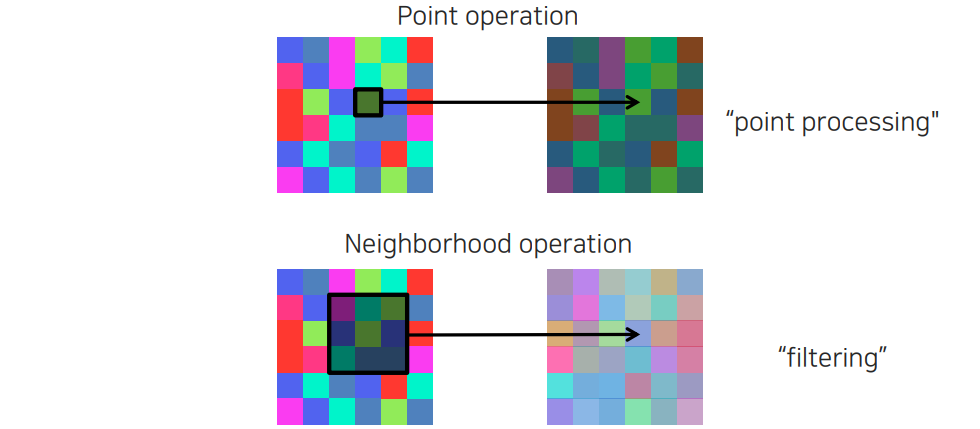앞서 image processing은 image filtering에 해당했다. 다시 image filtering은 2가지 종류로 나뉘게 되는데, 하나는 point operation이고 다른 하나는 neighborhood operation이다. Point-wise operation은 하나의 pixel 값 자체를 바꾸는 것이다. 이는 주변에 있는 값들하고 상관관계를 고려하지 않고 각 pixel마다 바꾸는 것이다. 반면, neighborhood operation은 주변 영역을 한번에 다보고 주변 정보를 참조해서 pixel 하나를 결정해주는 것이다. 우리는 이를 중점적으로 filtering이라고 부르지만 point operation을 하나의 부분 집합으로 생각할 수도 있다. 하지만 point operation은 point processing으로 부르고자 한다.
Point processing
먼저 point processing에 대해서 알아보고자 한다. Point processing에는 위와 같이 대표적으로 8가지 정도의 예시들이 존재한다. 일반적으로 사진을 찍는다고 했을 때 가장 많이 사용하는 point processing이라고 생각하면 된다. 밝기를 어둡게 만들 수도 있고 대조를 낮출 수도 있다. 부분적으로 밝기를 조절할 수도 있으며 전체적으로 조절할 수도 있다.
그렇다면 이를 어떻게 구현할까? 위와 같이 사칙 연산을 통해서 간단하게 구현할 수 있다. Image 가 8bit라고 하면 각 채널마다 256개의 값을 가지고 있을 것이다. 이 값들을 기반으로 사칙연산을 해주면 위와 같은 processing이 가능해지는 것이다. 특히 non-linear의 경우는 255로 나눠줌으로써 normalization을 해주고 여기서 제곱 등을 취해주면 linear한 mapping과는 대비해서 non-linear한 mapping이 형성되게 된다. 이를 통해서 밝은 부분을 더 밝게하는 것이 가능해지는 것이다.
Linear shift-invariant image filtering
이번에는 기본적인 image filtering 기법 중에서 영상이 살짝 움직여도 결과값이 비슷하게 나오는 shift-invarint image filtering에 대해서 알아보고자 한다. 흔하게 적용되는 image filtering이 바로 이 linear shift-invariant filtering일 것이다. 이 기법은 전체를 보고 linear combination을 고려해서 하나의 pixel을 고려하게 된다. 주변 pixel들을 고려해서 결합을 해줘야하는데, 여기서 결합해주는 가중치를 kernel이라고 부르게 된다. Filter의 kernel 자체를 어떻게 디자인하느냐에 따라 filter의 특징이 결정되게 된다. 그리고 같은 kernel을 사용했을 때, filter는 그 크기가 영상의 크기보다 작은 patch이고 이는 움직이면서 filtering을 수행할 것이다.
Shift-invariant라고 하는 것은 영상이 2개가 있다고 가정해볼 것이다. 정말 똑같은 사람이 위치만 달라져 있다고 생각할 것이다. 이를 가정했을 때, 해당 위치에서 똑같은 filter를 적용했을 때 그 값은 같아야 할 것이다. 물체가 이동했다고 하더라도 고유한 컨텐츠에 대한 filtering 결과값은 동일하다는 것이 shift-invariant 특성이다. 그렇다면 linear shift-invarinat filter는 어떻게 구현을 할까?
Convolution for 2D discrete signals
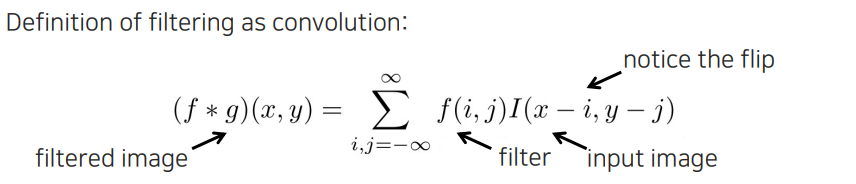Linear shift-invariant filter는 convolution operation으로 구현이 가능하다. Image processing이 어떻게보면 signal processing의 2D 버전이라고 볼 수 있다. 그래서 signal processing에서의 많은 것들을 적용시켜볼 수 있다. 위의 식에서 범위는 무한이지만 실제로는 filter의 크기를 특정하게 해서 사용하게 된다. 그리고 2D convolution 정의 자체에 flip이 들어가 있다. 실제로 에서 가 커지면 우측으로 가지면 image에서는 반전되어 반대로 가게 된다.
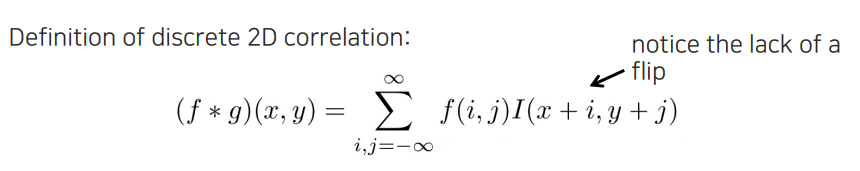Signal processing에서는 signal을 뒤집지 않고 2D correlation을 구할 수 있지만, image processing에서는 오른쪽으로 가면서 동일한 방향으로 filtering을 하게 된다. 그래서 만약 convolution과 correlation에서 동일한 를 사용하게 된다면 그 결과는 다르게 나올 것이다. 하지만 서로의 결과가 같고 image가 같다고 치면 서로의 filter는 뒤집힌 관계가 나올 것이다. 그래서 convolution을 구현하든 correlation을 구현하든 상관없이 image의 filter의 flip 관계만 고려해주면 크게 문제가 생기지 않는다. 특히 symmetric한 filter를 사용하면 큰 상관이 없을 것이다. Image processing에서는 심지어 symmetric하지 않은 경우에서는 flip을 고려해야 하지만, 나중에 deep neural network에서는 flip이 사실 중요하지 않게 된다. 그때는 가 각 목적에 맞게 학습이 될 것이기 때문이다. Deep learning에서는 를 구하는 것이 목적이기 때문에 상관이 없어지는 것이다. 하지만 image processing에서는 flip을 잘 고려해주는 것이 정말 중요할 것이다.
Gaussian filter
그렇다면 이러한 filter에는 어떠한 종류가 있을지 알아보고자 한다. 대표적인 filter 중 하나는 바로 Gaussian filter이다. Image processing에서는 손으로 직접 filter를 디자인해야 한다. Gaussian filter는 가운데 값이 크고 주변 값이 작은 형태로 만들어지게 된다. 중심의 pixel로부터 멀어질수록 weight값이 작아지게 된다. Gaussian filter는 특정 distance를 정해놓고 잘라서 사용하게 되기 때문에 filter의 크기가 크지않다. 2D Gaussian filter를 일반적으로 자르는 기준은 2에서 3 시그마로 정하게 된다.
우리가 Gaussian filter를 영상에 적용하게 되면 위와 같이 blurry한 결과를 얻을 수가 있다.
Guassian filter를 적용한 결과를 보면 blurry해졌지만 전체적인 디테일이 살아있는 것을 확인할 수 있다. Box filtering은 그저 평균을 내는 것이기 때문에 좀 더 직선의 구조가 더 강조되는 것을 확인할 수 있다. 이렇게 우리는 어떠한 filter를 사용하는지에 따라 다른 결과를 만들 수가 있는 것이다.
Other filters
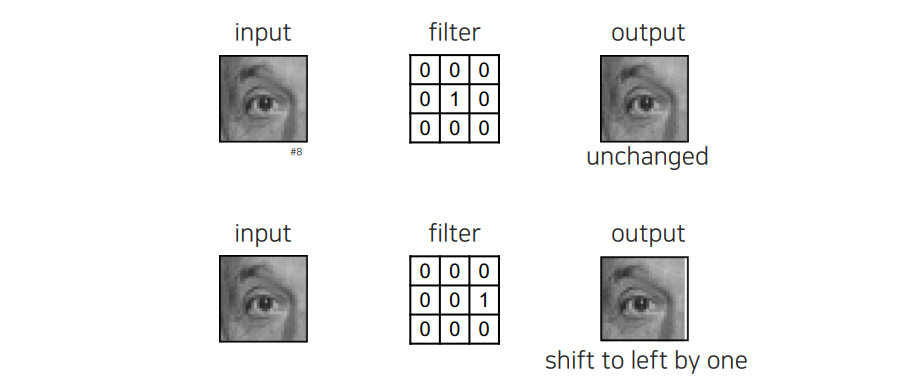이외에도 다양한 filter를 만들 수가 있다. 자기 자신을 만들어내는 filter를 구현할 수도 있고, 옆으로 한칸 이동시키는 filter도 구현할 수가 있다. Geometric transformation을 이야기 했을 때 좌표를 바꾼다고 했는데, 단순하게 이동시키는 operation의 경우에는 filtering으로도 구현할 수가 있다.
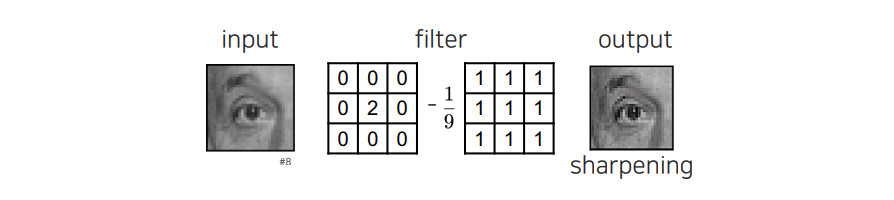또 다른 filter로는 box filter와 delta filter를 통해서 영상을 더 sharp하게 만들 수가 있다. 이러한 filter는 high-pass filter로서 역할을 하며, 원래 정보는 유지가 되고 high frequency 부분만 2배 강조가 될 것이다. 결국 이 filter의 원리는 intensity가 큰 부분에 대해서는 더 강조시키게 되는 것이다.
Sharpening 된 결과를 살펴보면 patch에서는 큰 차이를 느끼지 못했을 수 있지만, 전체적으로 영상에 적용된 결과를 보면 확실히 강조가 된 것을 확인할 수 있다. 명암이나 선명도가 높아져 화질이 좋아진 효과를 볼 수 있다.
Image gradients
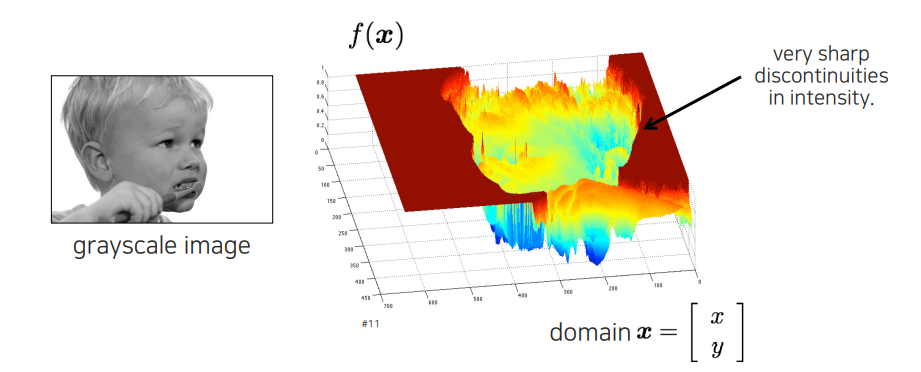Image gradient는 image의 edge 정보를 추출하는 것이다. Image에서 edge 정보는 굉장히 중요한 정보를 가지게 된다. 어떠한 image에서 object의 면에 대한 정보 보다는 shape에 대한 정보를 보고서 더 많은 정보를 얻을 수가 있다. 생각해보면 어떠한 물체가 있을 때, 색이 다른 컵이 있다고 할지라도 다 컵이기 때문에 이를 판다하기 위해서 shape을 보게 된다. 이러한 shape은 intensity의 변화가 큰 곳에서 쉽게 찾을 수가 있다. Edge 정보는 결국 shape을 판단하는데 중요한 정보가 되는 것이다.
Detecting edges
그렇다면 이러한 edge는 어떻게 찾는 것일까? 즉, function의 discontinuity를 어떻게하면 찾을 수가 있는 것일까? 이러한 function의 빠르게 바뀌는 부분은 일반적으로 미분을 활용하게 된다. 미분값이 크면 그 변화가 크다는 것이기 때문에 찾아낼 수가 있는 것이다. 이러한 미분을 discrete한 image에 적용하기 위해서는 discrete한 미분 식을 정의할 필요가 있다. 여기에는 미분 대신에 차분(finite difference)를 이용하면 된다.
Finite differences
차분은 미분을 정의하는데 있어 기본적인 limit 정의로부터 시작된다. 2개의 값을 비교하는데 그 간격만큼의 차이를 비교하게 되고, 여기서 limit를 이용하면 해당 function의 순간 기울기를 찾을 수가 있다. 하지만 discrete에서는 를 0으로 보내는 것이 의미가 없다. 그래서 central difference를 정의하게 된다. 중심의 0 값을 기준으로 둘 사이를 빼는 형태로 미분을 다시 정의하게 된다. 그 다음에 discrete signal 상태를 취급하기 위해서 의 간격을 2로 설정하게 된다. 그러면 그 결과 정수가 되기 때문에 pixel 좌표계에서 pixel 하나하나 간격으로 정의할 수 있게 된다.
우리는 이에 해당하는 convolution kernel도 정의할 수 있게 된다. -1, 0, 1인 kernel과 1, 0, -1인 kernel 중에서 어떠한 kernel이 맞을까? Image가 일반적으로 우측과 아래로 갈수록 값이 늘어나게 된다. 그래서 우리는 -1, 0, 1 kernel이 맞을 것이라고 생각할 수 있다. 하지만 여기서 빼놓은 부분이 있다. Convolution kernel에는 flip 개념이 있어 영상을 뒤집어야 하지만, 일반적으로는 영상은 그대로 두고 kernel을 반전시키게 된다. 그래서 우리는 convolution kernel을 사용하기 위해서는 1, 0, -1 kernel을 사용해야 하는 것이다. 1D derivative filter라고도 하며 이를 통해서 convolution을 할 수 있는 것이다.
Sobel filter
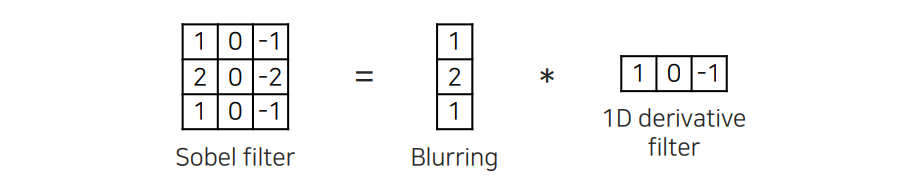앞서 1D derivative filter를 그냥 사용하는 것보다는 위와 같은 sobel filter와 같은 형태로 만들어서 사용하게 된다. Blurring을 하는 filter와의 convolution을 통해서 사용하게 되는데, blurring filter의 특징을 살펴보면 이는 Gaussian filter와 같은 역할을 하게 된다. 이는 실제로 low-pass filter를 이용해서 denoising을 통해서 noise를 제거하고 1D derivative filter를 취했다고 생각할 수 있다. 아무래도 1D derivative filter가 high-frequency component를 강조하기 때문에 noise가 증폭되는 효과를 방지해주기 위해서이다. 이러한 sobel filter가 자세히보면 방향성이 강조되어 있다. Sobel filter는 형태를 보면 아무래도 왼쪽과 오른쪽의 극명한 차이를 찾기 때문에 vertical edge들을 잘 찾을 수가 있게 된다.
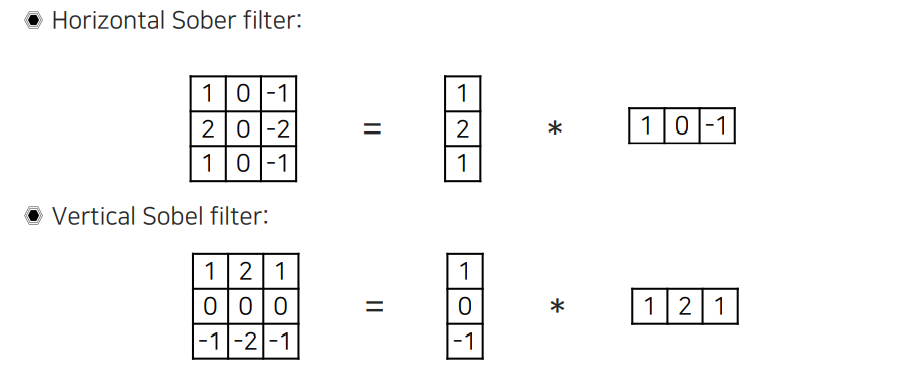그래서 filter의 형태에 따라 vertical line을 잘 찾게 되면 이를 horizontal sobel filter라고 하며, 반대로 horizontal line을 잘 찾게되면 이를 vertical sobel filter라고 하게 된다. 이를 만들어주기 위해서는 1D derivative filter의 순서를 바꿔주기만 하면 된다.
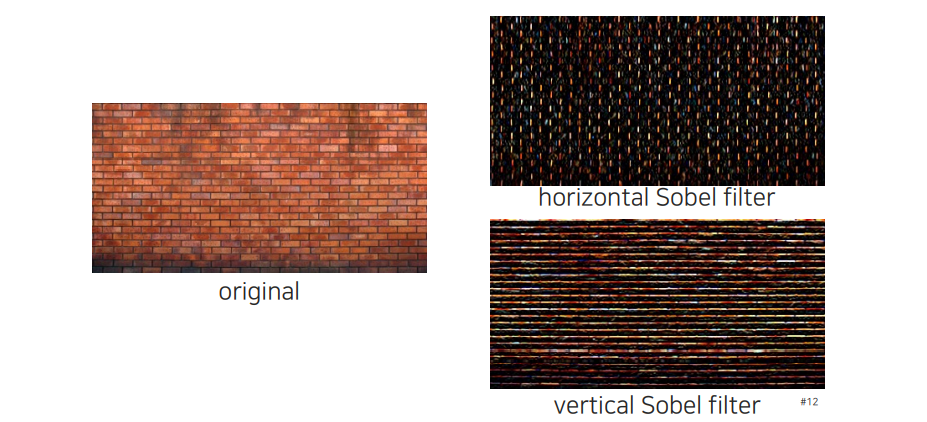어떠한 edge를 찾는지에 따라서 이름을 생각해보면 된다. Vertical line을 찾기 위해서는 horizontal sobel filter를 사용하면 된다. 반대로 horizontal line을 찾기 위해서는 vertical sobel filter를 사용하면 된다.
Computing image gradients
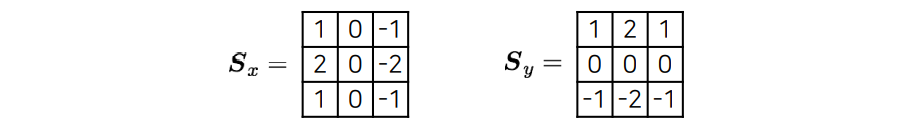지금까지 sobel filter를 어떻게 정의하는지 알아보았다. 축의 sobel filter와 축의 sobel filter를 위와 같이 정의해보았다. 우리는 이를 통해서 image의 gradient를 얻을 수가 있었다. 그러면 우리는 이제 이를 이용해서 convolution을 해야한다.
영상에다가 적용하게 되면 각각의 partial derivative를 얻을 수가 있다. 하지만 이는 정확하게 gradient를 의미하는 것이 아니다.
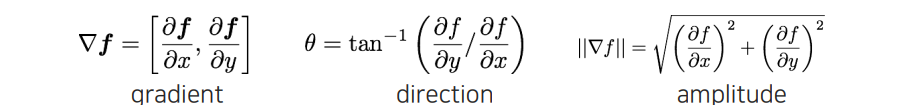Gradient는 이러한 partial derivative를 모두 모아야만 한다. 위와 같이 모아서 gradient를 정의하게 되면, 이로부터 amplitude를 구해서 방향과 상관없이 거기서 edge의 정도가 얼마나 큰지 energy를 측정할 수 있게 된다. 그리고 미분값의 비율에서 arctan을 통해서 방향을 구할 수도 있다.
Gradient의 amplitude를 계산하면 전반적인 모든 edge에 대해서 높은 영상을 만들 수가 있다.
How do you find the edge of this signal?
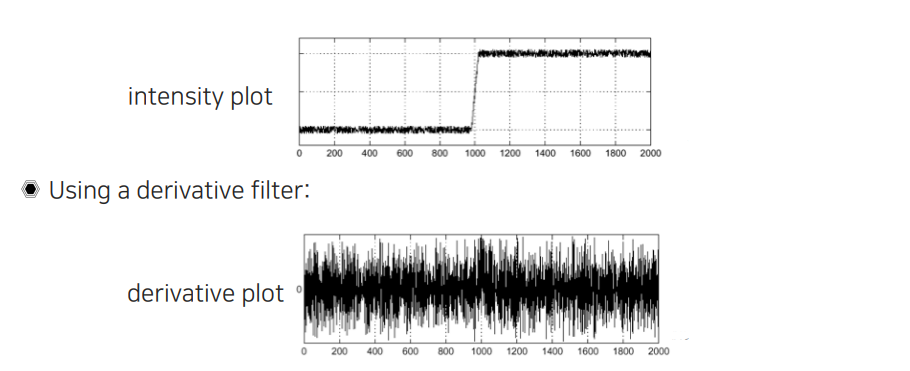이제 edge response를 구해서 edge 위에서는 높은 값을 띄우고, edge가 없는 영역에서는 거의 값이 존재하지 않는 것을 gradient amplitude를 통해서 확인할 수 있었다. 그렇다면 gradient amplitude를 구할 수 있었을 때, 해당 edge의 위치는 어떻게 찾을 수가 있을까? Image가 2D로 있을 때 가로로 그어서 intensity가 어떻게 변하는지 위와 같이 signal로 보고 있는 것이다. Derivative filter를 이용해서 convolution filtering을 취하면 위와 같이 noise가 많은 결과를 얻을 수가 있다. 그러면 이러한 noise로부터 edge를 어떻게 깨끗하게 찾을 것인지가 우리의 고민이다.
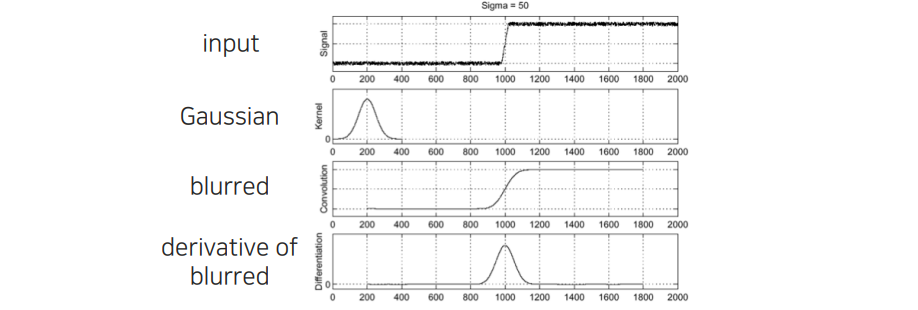Noise 성분은 일단 high frequency이다. Noise를 제거하고 싶으면 low pass filter를 취하면 된다. 대표적인 예시로 Gaussian filter를 이용해서 blur 시키면 noise가 사라지고 동시에 edge마저도 blur 처리가 될 것이다. 이렇게 blur 처리를 시키게 되면 noise 부분이 깔끔해진 것을 확인할 수 있다. Edge response 부분도 조금 blur가 되었지만, 여기다가 미분을 취하게 되면 noise가 있었던 부분은 filtering을 했기 때문에 밑으로 깔리게 되고, transition이 큰 부분만 edge point로 찾을 수 있게 된다.
Derivative of Gaussian (DoG) filter
그래서 우리는 이러한 2가지 operation을 따로따로 취하는 것이 아니라 한가지로 합쳐서 사용할 수가 있다. 이렇게 합친 filter를 derivative of Gaussian (DoG) filter라고 한다. 기존의 filtering을 생각해보면 영상에 filtering을 취하고 미분을 했다. 하지만 이는 모두 linear filter이고 우리는 이를 순차적으로 적용했던 것이다. Linear의 장점은 순서를 바꿔서 적용할 수 있다. 그래서 Gaussian filter를 미분해서 영상에다가 filtering을 단 한번으로 처리할 수 있게 된다. 그 형태는 다음과 같아지게 된다.
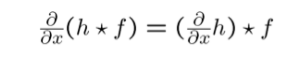이를 미리 계산해 놓으면 단 한번의 filtering만 하게 되고, 이는 다음과 같이 처리가 될 것이다.
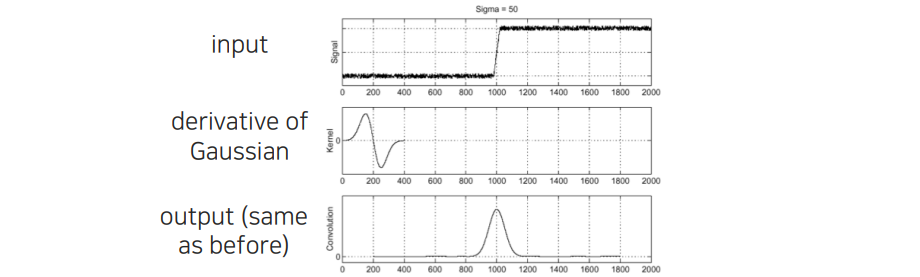그래서 edge point를 찾을 때 Gaussian filter처럼 denoising과 미분을 동시에 처리할 수 있게 되는 것이다. 이를 통해서 operation을 굉장히 아낄 수가 있게 되고, noise에 robust해지게 만들 수가 있다. 더불어 분석하는 면에서도 더욱 쉬워지게 된다.
Laplacian of Gaussian (LoG) filter
DoG filter 말고도 이와 비슷하게 Laplace filter도 존재한다. Laplace filter는 second-order filter로서 기존의 first-order finite difference가 아닌 second-order finite difference를 이용하여 적용시킬 수가 있다.
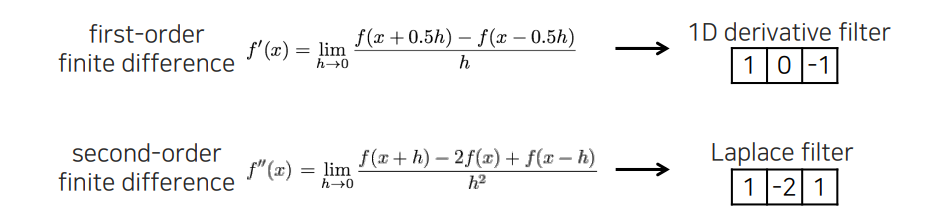Second-order는 다시 미분의 정의로부터 를 finite하게 정의하면서 만들면 된다. 각각의 coefficient가 1, -2, 1이기 때문에 이를 그대로 filter로 만들어서 사용할 수 있고, 이를 우리는 Laplace filter라고 하는 것이다.
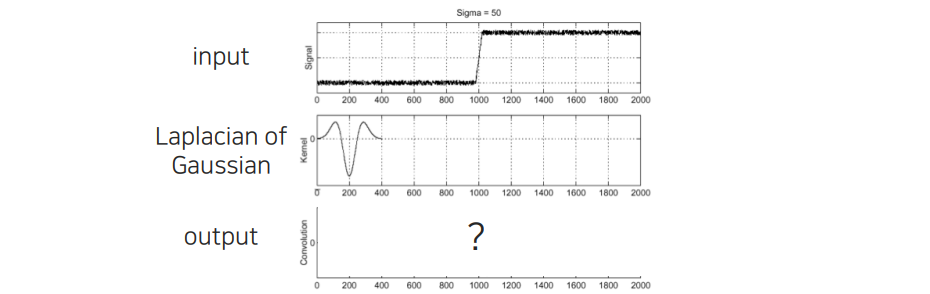우리는 Laplace filter를 이용해서 DoG filter처럼 Laplace filter와 Gaussian filter를 합쳐서 사용할 수 있다. 이를 Laplacian of Gaussian (Log) filter라고 부르며, 이 또한 2가지 operation을 한번에 사용할 수 있게 된다. 이전에 DoG filter에서는 maximum 값을 찾으면 그 지점이 edge가 되었다. 하지만 LoG filter에서는 zero crossing point를 찾아야 한다. 미분값이 양수에서 음수로 바뀌는 부분을 찾아야 하는 것이다.
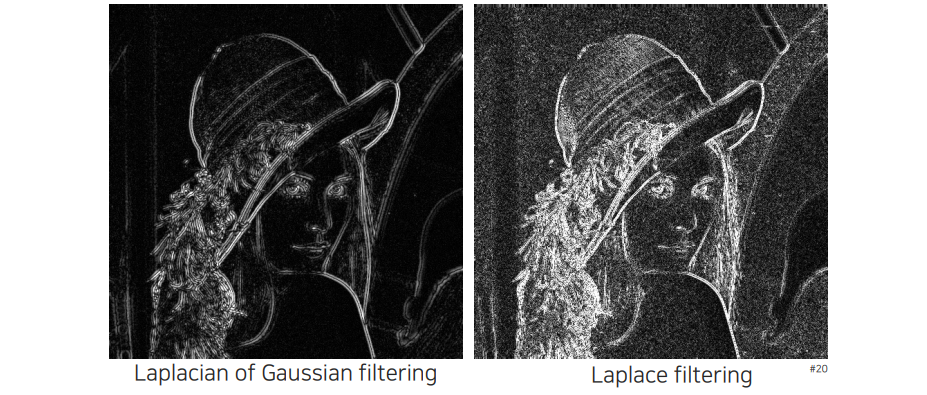그래서 LoG filter를 적용한 결과를 보면 Laplace filter에 비해서 noise가 굉장히 적은 것을 확인할 수 있다. 다만 edge가 근처에서 겹쳐 보이는 현상을 볼 수 있다. 아무래도 양수와 음수 모두 표현되기 때문이다.
DoG vs LoG
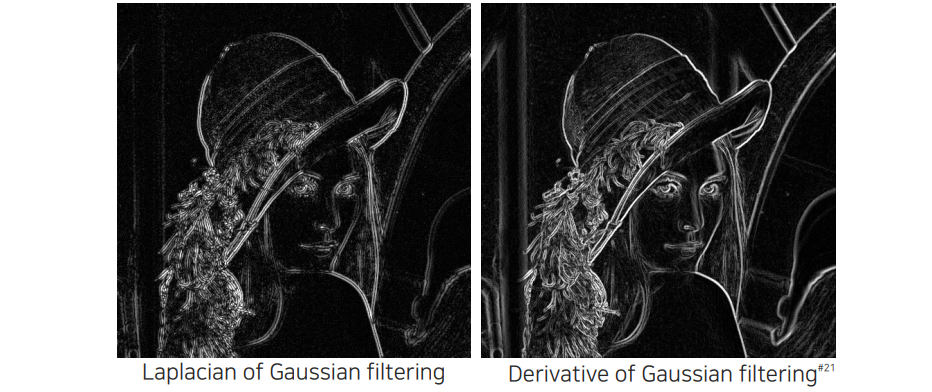LoG filter와 DoG filter의 결과를 비교해보면 둘다 깨끗하게 denoising 되는 것을 확인할 수 있다. Sobel filter하고는 다르게 좀 더 Gaussian filter를 이용한 blur와 derivative를 더 잘 이용한 결과가 된다.
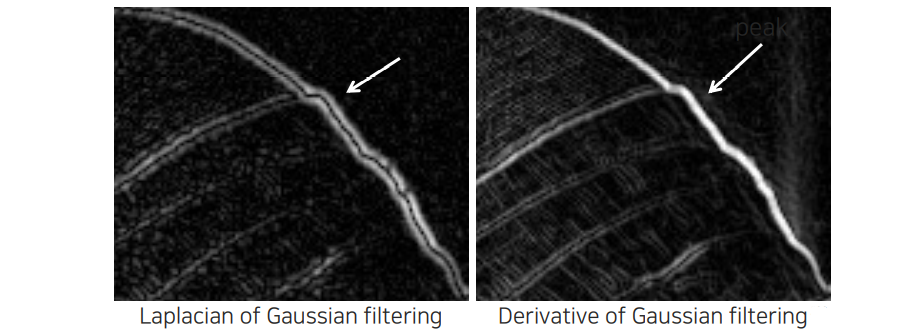Maximum point를 찾는 것보다 일반적으로 zero crossing point를 찾는 것이 소수 pixel 단위에서는 훨씬 정확한 결과를 만들게 된다. 하지만 zero crossing point를 찾는 것이 더 쉽다고 이야기하기는 어렵다.
2D Gaussian
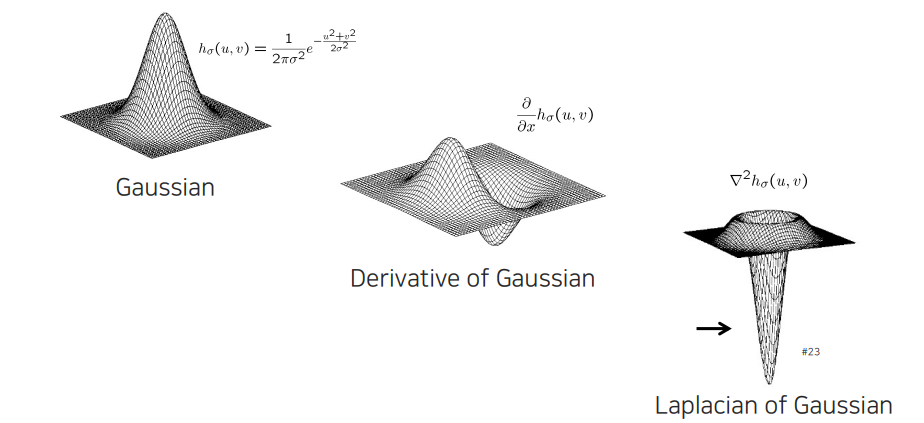2D Gaussian filter로부터 DoG와 LoG를 표현한 것이다. 아무래도 우리가 보는 영상은 2D이기 때문에 2차원의 공간에서 적용할 필요가 있다. DoG filter를 보면 축과 축으로 따로 정의해서 사용할 수 있다. LoG filter는 모든 방향에 대해서 적용되기 떄문에 방향성이 존재하지 않고, 가운데 부분과 주변 부분의 차이를 극명하게 찾는 것을 굉장히 잘한다.
