Big-O 표기법 사용 이유
수행 시간을 분석하는 것이 정말 중요함을 계속해서 강조하고 있다. 분석을 잘못하였을 경우 큰 오류가 생길 수 있지만, 반대로 너무 자세하게 분석을하는 것도 문제가 될 수 있다. 그래서 정확한 정보를 알려주는 분석을 위해서 적절하게 단순화하는 작업이 필요하다.
수행 시간을 컴퓨터 기본 연산들로 표현하는 것 자체가 이미 단순화한 것이다. 컴퓨터 구조에 맞게 사소한 것까지 고려하여 수행 시간을 분석하다 보면 너무 복잡해져 이 또한 사용하기에 용이하지 못하다. 그래서 보다 간단하면서 컴퓨터와 독립적인 알고리즘 성능 분석 방법을 찾게 되는 것이고, 이러한 것들을 고려하여 입력의 크기에 따른 컴퓨터 기본 연산의 개수를 세는 것으로 우리는 알고리즘의 수행 시간을 나타내게 된 것이다.
이러한 단순화 작업에서 우리는 또 단순화를 하고자 한다. 만약 입력의 크기가 n일 때, 알고리즘의 수행 시간이 이라고 한다면, 이걸 전부 사용하지 말고 최고차 항 외의 항(4n + 3)을 무시하고 더 나아가 최고차 항의 계수 또한 무시하고자 한다. 그렇게 남은 것이 이고 우리는 이라고 표기할 것이다.
시간복잡도 T(n)
우리는 앞으로 수행 시간을 찾을 때 T(n)을 구해볼 것이고, 이 T(n)은 n개의 입력이 있을 때, 알고리즘이 이 입력 n개에 대하여 연산을 수행하는 횟수를 나타낸다. 즉, 입력 크기에만 종속이 된다.
Big-O 표기법(Big-O notation)
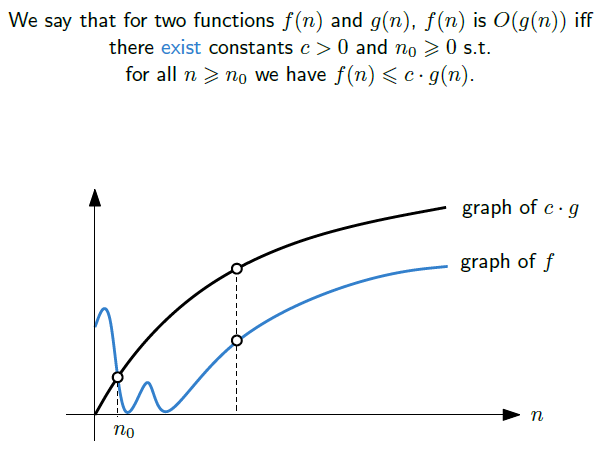
어떤 함수 f(n)의 Big-O 표기법이 O(g(n))이라고 하면, n의 값이 일정 수준을 넘어 충분히 큰 값이라고 한다면, 그 이상의 어떤 n을 대입하더라도 c * g(n) 보다 결과값이 작은 상수 c가 존재한다는 의미다.
Big-O 표기법은 보통 알고리즘에서 시간의 상한인 최악의 경우를 가정할 때 사용한다. 즉, 가장 오래 걸릴 경우의 시간 복잡도를 표기할 때 사용하게 되어 해당 알고리즘은 Big-O보다 더 오래 걸릴 수 없음을 알 수 있다.
Big-Ω 표기법(Ω-notation)
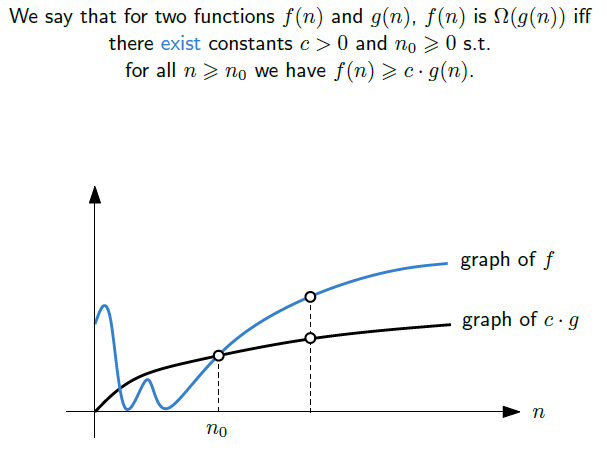
Big-Ω 표기법은 알고리즘에서 시간의 하한인 최선의 경우를 가정할 때 사용한다. 즉, 가장 빨리 걸릴 경우의 시간 복잡도를 표기할 때 사용하게 되어 해당 알고리즘은 Big-Ω 보다 더 빨리 걸릴 수 없음을 알 수 있다.
Big-Θ 표기법(Θ-notation)
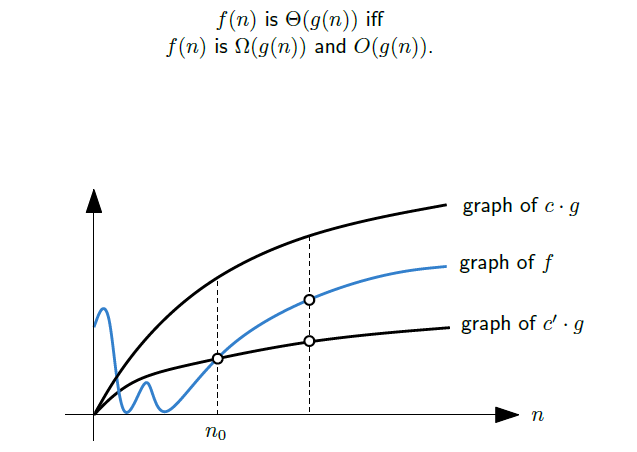
Big-Θ 표기법은 알고리즘에서 평균적인 경우를 가정할 때 사용한다. 즉, 딱 맞는 수행 시간의 시간 복잡도를 표기할 때 사용하며, 이는 Big-O와 Big-Ω를 하나로 합쳐 표현하게 된다.
현실에서는 항상 최악의 경우를 생각해야 하기 때문에 Big-O 표기법을 많이 사용한다. 반대로 최선의 경우는 생각보다 크게 사용되는 경우가 없을 것이다. 대부분의 알고리즘은 특정 데이터를 가지고 O(1)에 도달할 수 있게 할 수 있다.
성질과 규칙
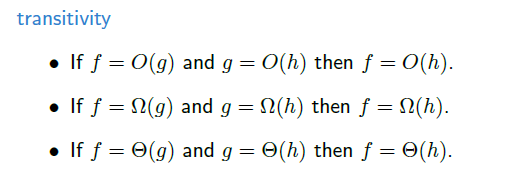
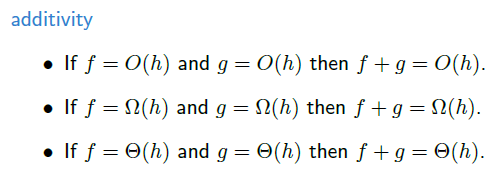
상수 곱셈은 무시할 수 있다. 즉, 계수가 몇이든 신경쓰지 않아도 된다.
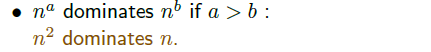n의 지수가 클수록, 큰 지수쪽이 더 빨리 증가한다. 이것은 일반적으로 생각하기 쉬운 부분이다.
임의의 지수 함수는 다항 함수보다 빨리 증가한다.
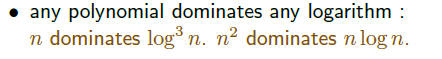임의의 다항 함수는 로그 함수보다 빨리 증가한다.
위의 성질과 규칙들을 보고 우리는 상수는 무조건 무시해야 한다고 생각해서는 안된다. 프로그래머들과 알고리즘 개발자들은 이 상수에 조차 초점이 맞춰져 있기에 소홀히 해서는 안되는 부분이지만, 우리가 공부하고 배우는 알고리즘 수준에서는 Big-O 표기법을 사용해서 간단히 생각하고자 할 것이다. 그렇지 않다면 알고리즘들을 이해하는데 있어 어려울 수 있다.
