Convex Hulls의 정의
Convex Hulls이란 무엇인가? 조금 어렵게 이야기 하면, 2차원의 유클리드 좌표에서 어떠한 점들의 집합이 만든 다각형이 다른 모든 점들을 포함하는 점들의 집합을 이야기 한다. 조금 쉽게 말함면 여러 개의 점이 주어졌을 때, 이 모든 점들을 포함하는 최소 크기의 볼록 다각형을 Convex Hulls이라 한다.
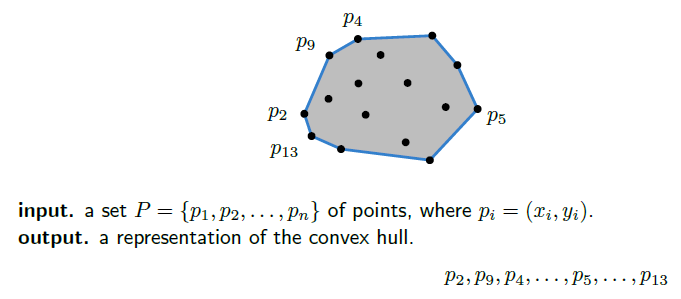
이 Convex Hulls의 input과 output을 다음과 같이 정의할 수 있다. Input은 어떤 x좌표와 y좌표가 하나의 점 p라고 했을 때 이 p들의 집합이다. Output은 이 점들의 집합 중 모든 점들을 포함하는 점들의 집합을 다음과 같이 표기할 수 있다.
Convex Hulls의 가정
이 Convex Hulls 문제를 풀기 위해서 우리는 P 집합의 점들은 일반적인 위치에 있다고 생각할 것이다. 즉, 어떠한 3개의 점도 공통된 한 라인을 만들지 않아야 한다.
그리고 3개의 점 p, q, r이 존재할 때, r이 p와 q가 이루는 직선의 왼쪽인지 오른쪽인지 어떻게 판단할 것인가? 바로 다음과 같이 기울기의 개념을 가져와 하나의 점이 다른 두 점이 이루는 직선의 어느 방향에 존재할지 판단할 것이다.
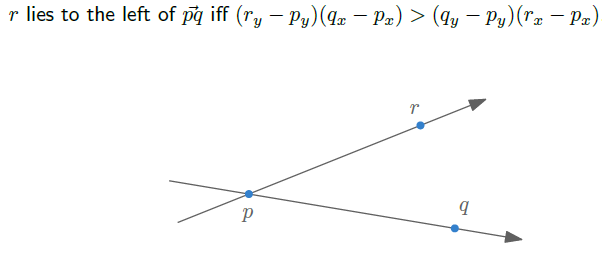
위 식을 조금 다르게 살펴보면, r과 p의 기울기가 q와 p의 기울기보다 큰 것을 알 수 있다. 만약 반대 상황이 된다면 r은 p와 q가 이루는 직선의 오른쪽에 있음을 알 수 있을 것이다.
Convex Hulls 알고리즘
이 Convex Hulls을 구하는 문제는 여러 알고리즘이 존재하지만, 우리는 Brute force 방법과 가장 유명한 Graham's scan을 통해서 알아보고자 한다.
1. Brute force
Brute force란 쉽게 말해서 가능한 경우를 모두 다 해보는 것을 말한다. 시계 방향으로 점들을 보게 된다면, 다른 점들이 모두 오른쪽에 있으면 된다. 그렇기에 점 p와 q를 순서대로 잡고, 다른 모든 점들이 이 p와 q가 만드는 직선의 오른쪽에 놓여있는지 확인하면 된다. 그리고 만약 오른쪽에 존재한다면, 이 p와 q를 선택하면 되는 것이다.
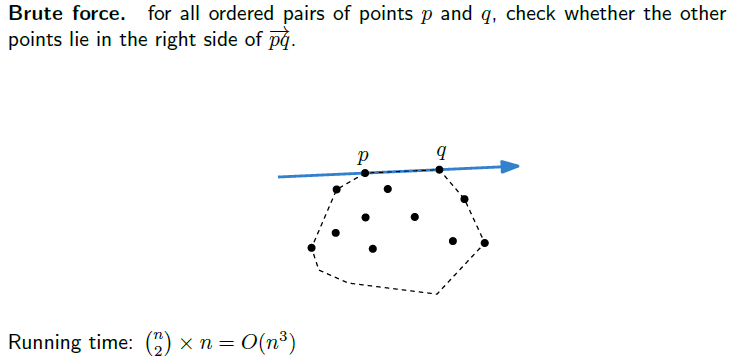
사실 이 경우 정확한 결과를 낼 수 있지만, 모든 경우를 생각해야 하기에 시간적인 효율이 굉장히 떨어진다. 그렇기에 Running Time이 n개의 점들 중 2개를 고르는 시간(nC2)과 뽑힌 2개의 점들을 가지고 나머지 점들을 확인하는 시간이 필요하기에 n3 시간이 필요하다. 이를 Big-O 표기법을 사용해서 O(n3)라고 하지만, 이는 뒤에서 설명할 예정이다.
2. Graham's scan
O(n3) 괜찮지 않겠냐고 생각할 수 있지만, 우리는 이보다 더 빠른 방법이 있다면 찾을 필요가 있다. 그렇게 나온 것이 Graham's scan 방법이다.
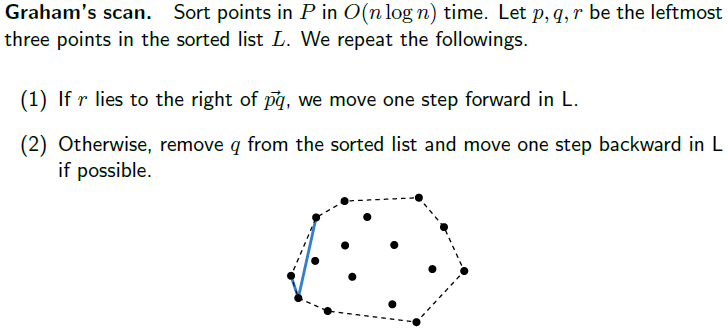
결론부터 말하자면 이 알고리즘은 선형 로그적 시간(nlog2n)내로 해결이 가능해 앞서 구한 방법보다 더 효율적으로 구할 수 있다.
Graham's scan의 방법을 살펴보면, 보통 x좌표를 기준으로 오름차순 정렬을 시키고 왼쪽부터 차례대로 p, q, r 3개의 점으로부터 다음 단계를 반복하면 된다.
(1) 만약 r이 p와 q가 이루는 직선의 오른쪽에 있다면(위에서 말한 방법 이용하여 판단), 다음 점들로 이동한다. 즉, 기존의 q가 p가 되고, r이 q가 되며, 다음 새로운 점이 r이 된다.
(2) 반대로 r이 왼쪽에 있다면, 가능하다면(이전 점이 존재한다면) q를 지우고 하나씩 이전 점들로 이동한다. 즉, 기존의 p가 q가 되고, r은 그대로 두며, 바로 직전의 점을 다시 p가 된다.
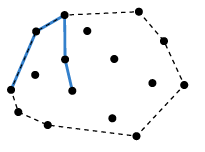
자세히 살펴 보면, 우리는 x축 기준, 왼쪽부터 p, q, r이라 할 것이다.
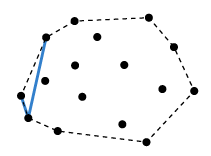
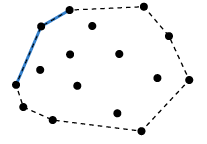
위 경우 r이 p와 q가 이루는 직선 기준 왼쪽에 있는데, 이전의 p가 없으므로 r이 q가 되고, 다음 점이 r이 된다.
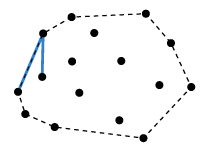
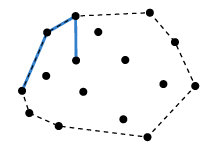
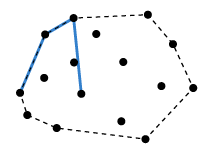
위 경우 r이 p와 q가 이루는 직선 오른쪽에 있으므로 (1)에 해당하여 기존의 q가 p가 되고, r이 q가 되며, 다음 점이 r이 된다. 그리고 기존의 p는 Convex Hulls에 포함시키면 된다.
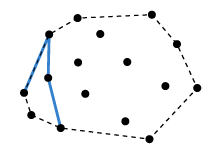
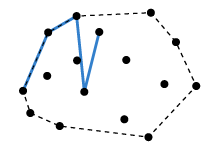
계속해보면, 위 경우 (2)에 해당하게 되고 이전 점을 p로 하고 기존의 p는 q가 되며, 기존의 q는 지워버리면 된다. 그러면 다음과 같이 기존 q자리의 점은 제외가 된다.
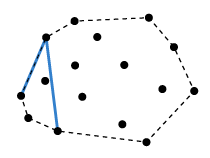
다시 위 경우에서 r이 오른쪽에 있어 (1)에 해당하므로 한개씩 앞으로 이동하면 된다.
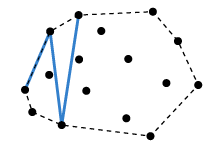
위의 경우는 (2)에 해당하므로 다음과 같이 된다.
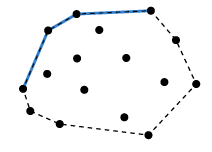
이렇게 계속 진행하다 보면 우리는 가장 외곽의 Convex Hulls 조합을 찾을 수 있게 될 것이다.
Graham's Scan 시간
(1)번을 수행하게 되면, 정렬된 리스트에서 점이 다음 점으로 총 n-2번 이동해가게 되기에 n의 시간만큼 필요하다.
(2)번을 수행하게 되면, 정렬된 리스트에서 점이 하나씩 총 n-h번 제거가 되기에 이 또한 n의 시간만큼 필요하다. (여기서 h는 Convex Hulls을 이루는 점들의 개수를 의미한다)
결과적으로 정렬(sorting) 과정에서 nlogn의 시간이 필요하고, Graham's scan 과정에서 n의 시간이 필요하기에 이 알고리즘의 최종 수행 시간은 O(nlogn)이라고 할 수 있다.
