최근접 점의 쌍 찾기(Find Closest Pair of Points)
우리는 n개의 점들이 평면에 주어졌을 때, 유클리드 거리(Euclidian distance)가 가장 적은 점의 쌍을 찾고 싶다. 어떻게 하면 될까?
1. Brute force - 총 n개의 점에서 나머지 n - 1개의 점들을 대상으로 하나씩 비교해가면 된다.
2. Divide and Conquer - 총 n개의 점들을 x축 기준으로 정렬하고, x의 중앙값인 점을 찾아 왼쪽과 오른쪽 점들로 문제를 나누어 최소 거리를 찾은 다음에 이를 바탕으로 중앙의 점을 포함하여 범위를 좁혀나가 최소 거리를 찾으면 된다.
x좌표를 기준으로 정렬이 되었고 x의 중앙값이 정해졌을 때, 우리는 리스트를 2개의 부분 리스트로 나누는 과정에서의 수행 시간은 O(1)이다.
그리고 y좌표를 기준으로 각각의 점들을 확인하면서, x좌표를 동시에 확인 했을 때, x가 x의 중앙값보다 작은지 큰지 판단하여 부분 리스트로 나누는 과정에서의 수행 시간은 O(n)이다.
그리고 우리는 δ를 좌측 그룹과 우측 그룹에서의 최소 거리로 정의하고, 이 거리를 이용해서 중앙값으로 부터 양쪽으로 δ만큼 거리 내에서의 최소값을 다시 확인할 것이다.
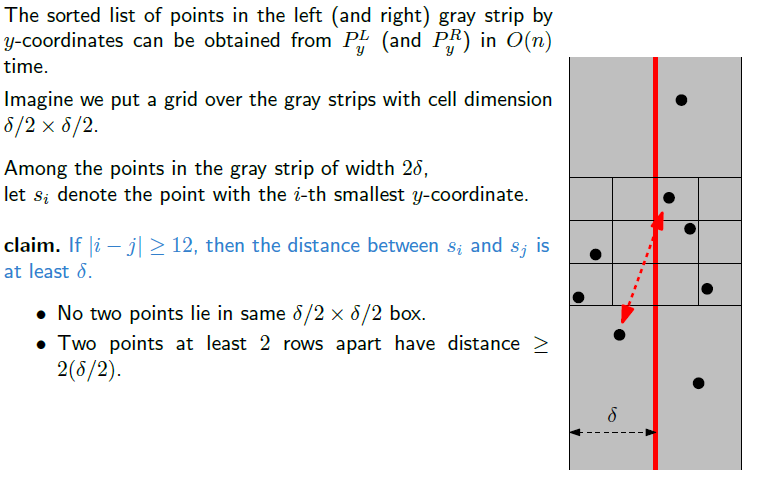중앙 부분만 따로 생각했을때 가로 길이는 2δ가 될 것이고, 이를 다시 반으로 나눈 상태에서 다시 반으로 나눠서 격자를 만들면 각 격자의 길이는 δ / 2가 된다. 그리고 이 격자 내에서 y좌표 값이 작은 순서대로 인덱스를 붙여나갈 것이다. 여기서 우리는 새로운 사실을 알 수 있다. 두 점의 인덱스 차가 12보다 크거나 같으면, 가령 첫번째 점과 13번째 점을 비교 대상으로 생각했다면, 이 점 사이의 거리는 적어도 δ가 된다는 것이다. 왜 그런 것일까? 만약 한 격자 내에 2개의 점이 들어가 있다면, 거리가 무조건 δ 보다 작으므로 이 두 점은 최근접 점의 쌍이 된다. 그리고 위의 그림처럼 3 * 4 격자 내에서 거리를 계산하면 되는데, 이 격자 밖은 거리가 δ보다 크기 때문에 11개의 격자에 대해서 계산을 하면 된다.
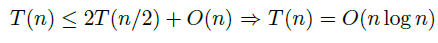n개의 점이 주어졌을 때, 2개의 부분 리스트로 나누고 크기도 반으로 줄여나가기에 Master theorem에 의해 a와 b는 2가 된다. 그리고 추가적인 연산으로 정렬된 리스트를 얻고 최대 n개의 점에 대해서 상수개의 점과 비교하기 때문에 d는 1이 된다. 여기서 y부분을 정렬하는데 있어 합병 정렬(Merge sort)와 동일하게 진행했을 때 수행 시간이 O(n)까지 좋아지는 것을 알 수 있었다. 따라서 최적의 수행 시간은 위와 같이 될 것이다.
