중앙값 찾기(Find Median)
숫자들의 중앙값(Median)은 리스트가 존재할 때 정중앙에 있는 값으로, 이 값을 기준으로 절반은 이 값보다 작고, 나머지 절반은 이 값보다 크다. 간단하게 예를 들어 리스트 [45, 1, 10, 30, 25]가 있을 때, 중앙값은 25가 된다. 왜냐하면 이 숫자들을 크기 순서대로 배치하게 되면 [1, 10, 25, 30, 45]가 되어 홀수개의 원소는 중앙값이 정확하게 가운데 숫자기 때문에 25가 된다. 만약에 이 리스트의 길이가 짝수일 경우, 무엇이 중앙값이 될지 2가지 선택이 있다. 어느 경우에든 둘 중에서 더 작은 것을 선택하면 된다.
중앙값을 찾는 목적은 하나의 전형적인 값으로 숫자들의 집합을 요약하려고 하는 것이다. 보통 리스트에서 어떠한 값을 찾을 때, 평균(Mean)이나 중앙값이 자주 사용이 된다. 중앙값은 평균에 비해 데이터에 더 전형적이다. 아무래도 항상 주어진 데이터에서 하나의 값을 뽑아낼 수 있기 때문이다.
n개의 데이터에서 중앙값을 계산하는 것은 쉽다. 하지만 쉬운만큼 수행 시간이 O(nlogn)으로 이상적이지는 못한다. 우리는 선형적인 시간을 선호하기에 이 수행 시간을 더 효율적으로 개선시킬 수 있으면 좋다.
우리는 앞으로 재귀적인 해를 찾을 때, 그 문제의 좀 더 일반적인 상황으로 문제를 해결할 것이다. 그래서 우리는 굳이 중앙값이 아니고, 어떠한 리스트에서 어떠한 값을 찾아내는 상황을 생각해볼 것이다.
선택(Selection)
선택(Selection)은 어떤 리스트 S와 정수 k가 주어졌을 때, S에서 k번째로 작은 원소를 찾아내는 과정이다.
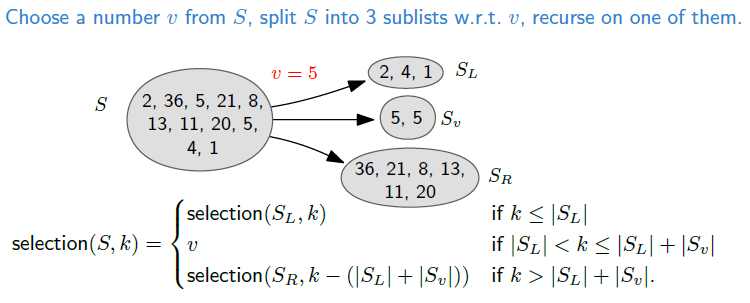여기서 우리는 어떤 숫자 v에 주목할 것이다.(v는 k를 찾기 위한 임의의 값) 리스트 S를 3개의 범주로 나누었을 때, v보다 작은 원소들, v와 같은 원소들(중복 포함), 그리고 v보다 큰 원소들로 나눌 수 있다. 예를 들어 위의 그림에서 v = 5라고 했을 때, [2, 4, 1] / [5, 5] / [36, 21, 8, 13, 11, 20]으로 나눌 수가 있다. 이렇게 나누었을 때, 탐색 단계에서 3개의 부분 리스트들 중 하나로 좁혀나갈 수 있다. 만일 S의 8번째로 가장 작은 원소를 찾아야 한다면, 첫번째 리스트와 두번째 리스트의 원소 개수의 합은 5이기 때문에 자동적으로 마지막 리스트의 3번째 값이 된다. 즉, selection(S, 8) = selection(SR, 3)이 되는 셈이다. 좀 더 일반적으로 부분 리스트의 크기에 따라 k를 검사함으로써, 이 리스트들 중 어느 것이 원하는 원소를 지니고 있는지를 빠르게 결정이 가능하다.
v는 어떻게 고르는가?
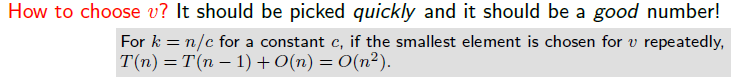우리는 v를 고를 때 빠르게 선택하고 이것이 원하는 k에 근접하면 정말 좋을 것이다. 가장 이상적인 경우는 v를 선택했을 때, SL과 SR의 크기가 S의 절반이면 될 것이다. 그러나 이것은 v가 궁극적인 목적으로 중앙값이여야 한다.
자연스럽게 알고리즘은 v를 어떻게 선택하느냐에 따라 수행 시간이 달라질 것이다. 만약 가장 좋지 않은 경우로 가장 앞의 원소와 가장 뒤의 원소가 v로 선택이 되어질 경우 기존의 알고리즘보다 수행 시간이 더 좋지 않아질 수 있다.
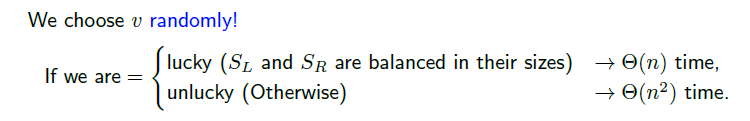그러면 우리는 어떻게 해야 하는가? v를 임의로 선택하면 된다. 이 무슨 말도 안되는 소리인가 생각하겠지만, 실제로 v를 가운데 어느 지점에서 선택하게 되었을 때, 좋지 않은 케이스가 나오는 경우는 꽤 드물어진다.
만약 100개의 원소 중 25번째 원소를 택한다고 했을 때, 부분 리스트 중 길이가 가장 길어봐야 원래 리스트의 3 / 4 크기이다.(우리는 25%와 75% 사이에 v가 놓이면 lucky case로 볼 것이다!) 임의로 선택이 된 v가 lucky case가 될 확률은 50%라는 것이 주어만 진다면, 우리는 수행 시간을 원하는대로 효율적으로 바꿀 수 있다.
예시를 하나 볼 것이다. "평균적으로 평평한 동전은 앞면이 보이려면 두 번은 던져져야 할 필요가 있다"를 증명할 것이다.
동전이 앞면이 보이기 전에 던져지는 기대 횟수(Expected number)를 E라고 하면, 분명히 최소한 한 번의 던져짐은 필요하고, 그것이 앞면이 나왔다면, 우리는 원하는 결과를 얻은 것이다. 만약 그것이 뒷면일 경우 다시 할 필요가 있다. 따라서 E = 1 + (1 / 2)E 이고, E는 2로 해결 된다. 그래서 우리는 평균적으로 2번의 분할하는 연산 후에 리스트는 길어봐야 원래 크기의 3 / 4 정도까지 줄어들 것이다. 위 수행 시간은 (3 / 4)n 크기의 리스트에 수행해야 하는 시간과 리스트를 (3 / 4)n 이하로 줄이기 위한 시간이 최종 수행 시간이 되는 것이고, 합의 성질을 이용해서 최종적으로 T(n) = O(n)이라는 결론을 내릴 수 있다.
