순환 관계(Recurrence Relations)
분할정복법 알고리즘은 보통 특정 패턴을 따르는데, 크기가 n인 문제가 있다고 했을 때 부분 문제들이 a개씩 분할이 되고, 각 문제들이 b의 크기로 나누어지며, 추가적으로 n의 d제곱만큼의 수행 시간이 요구되어지면, 이들의 수행 시간은 다음과 같은 수식으로 얻을 수가 있게 된다.
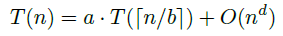그리고 이 수식은 Master theorem으로 해결할 수 있다.
Master theorem
Master theorem을 정의해보면, 재귀 관계식으로 표현한 알고리즘의 동작 시간을 점근적으로 계산하여 간단하게 계산하는 방법이다. a는 0보다 크고, b는 1보다 크며, d는 0 이상인 어떤 상수에 대해서 다음과 같이 계산할 수 있다.
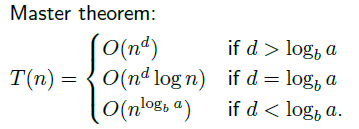이 하나의 정리가 얼마나 대단한지 앞으로 대부분의 분할정복법 문제를 풀다보면 느끼게 될 것이다.
Master theorem 증명
우리는 이 정리를 증명하기 위해서 n이 b의 거듭제곱이라고 가정하고 시작할 것이다. 이전의 곱셈도 2의 배수 크기를 2로 쪼개어 가다보니 이해가 쉽게 되었다.
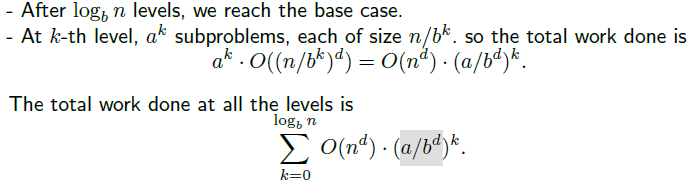부분 문제의 크기는 순환의 각 레벨로 b의 인수만큼 줄어들게 된다. 이렇게 logbn 레벨 후에는 base case에 도달하게 되고, 이것이 깊이가 되는 것이다. 그리고 앞서 a개의 branching factor로 부분 문제를 나누었기에 일반화 했을 때, k번째 레벨에서 수행된 수행 시간과 이를 처음부터 끝까지 순환했을 때의 수행 시간은 위와 같이 된다.
이제 a, b, d의 값에 따라 3가지 경우가 만들어질 수 있고, 이에 따른 수행 시간은 다음과 같이 정할 수 있다.
이렇게 해서 다음과 같이 Master thoerem이 일반화 될 수 있다.
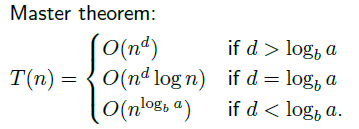
이진 탐색(Binary Search)
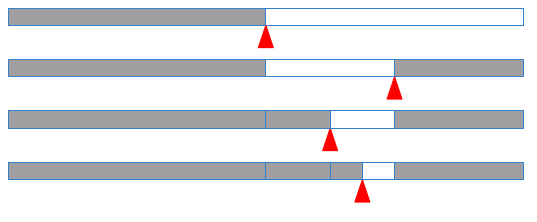이진 탐색(Binary Search)는 데이터가 정렬되어 있는 배열에서 특정한 값을 찾아내는 탐색 알고리즘 중 하나로, 배열 중간의 임의의 값을 선택하여 찾고자하는 값과 비교하게 된다. 이때, 값이 중간값보다 작으면 왼쪽, 크면 오른쪽으로 다시 탐색하면 된다.
정렬도니 순서로 z[0, 1, ... ,n - 1]와 같이 키(key)를 포함하는 큰 파일에서 특정 k를 찾기 위해서, 먼저 k를 z[n / 2]와 비교하고, 그 결과에 따라서 파일의 앞 부분(z[0, ... , n/2 - 1])을 순환시키거나 또는 뒷 부분(z[n/2, ... , n - 1]을 순환시킨다. 이 순환 과정은 1개의 부분 문제로 나누기에 a는 1이고, 이 문제는 크기가 절반이 되기에 b는 2이고, 이후에 추가 연산이 없기에 d는 0이 된다.
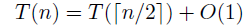이를 Master theorem에 대입해서 정리하면 수행 시간은 O(log n)이 되는 것을 알 수 있다.
