합병 정렬(Merge Sort)
숫자들의 리스트를 정렬하는 문제는 그 자신을 즉시 분할정복법(Divide and Conquer)에 따를 수 있다. 합병 정렬(Merge sort)은 '존 폰 노이만(John vodn Neumann)'이라는 사람이 제안한 방법으로, 하나의 리스트를 2개의 균등한 크기로 분할하고, 분할된 부분 리스트를 정렬한 다음 2개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다. 그래서 합병 정렬은 분할정복법으로 다음과 같은 단계를 가지고 있다.
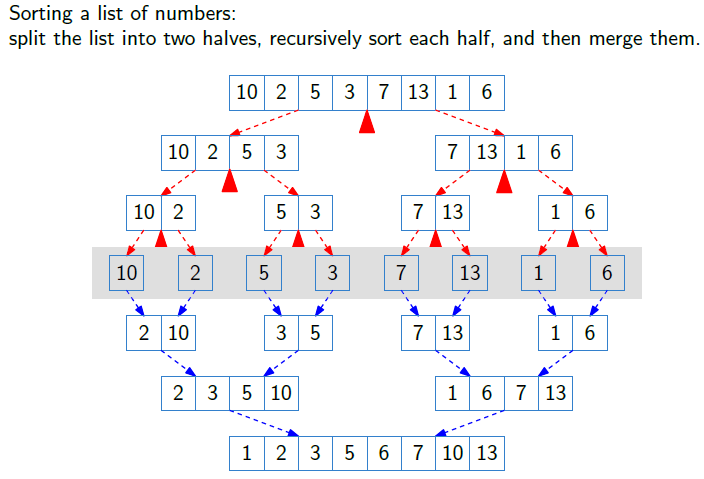
- 분할(Divide) : 입력 리스트를 같은 크기의 2개의 부분 리스트로 분할한다.
- 정복(Conquer) : 부분 리스트를 정렬하는데, 부분 리스트의 크기가 충분히 작지 않은 경우 다시 순환 호출을 통해서 다시 분할 정복법을 적용한다.
- 결합(Combine) : 정렬된 부분 리스트들을 하나의 배열로 다시 결합한다.
합병 정렬의 수행 시간은 우선 2개의 리스트로 분할하기 때문에 branching factor인 a는 2가 될 것이고, 분할된 리스트는 기존 리스트의 크기의 절반이 되므로 b는 2가 된다. 그리고 마지막 결합(combine) 단계에서 정렬된 2개의 리스트를 결합하기 단계는 선형 시간에 d는 1이 된다. 그래서 수행 시간을 Master theorem에 의하면 O(nlogn)이 된다.
합병 정렬의 하한 경계(Lower Bound of Merge Sort)
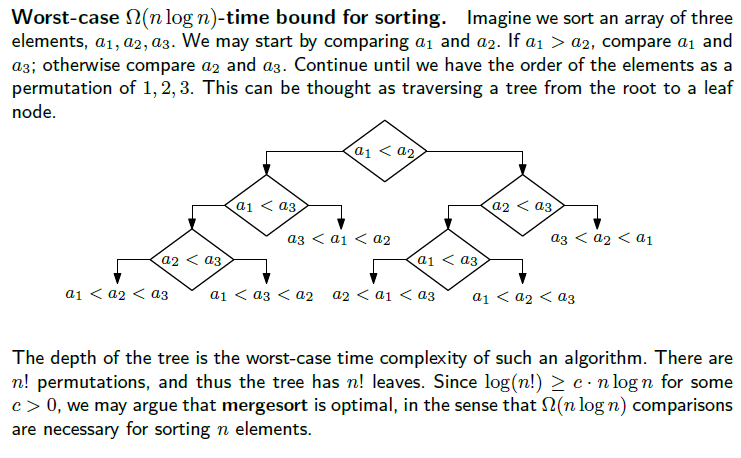정렬 알고리즘은 트리로서 설명이 가능한데, 위 트리에서는 원소가 3개일 때 배열을 정렬하는 경우를 모두 적은 것이다. 먼저 2개의 원소를 비교하고, 하나의 원소가 더 크면 이 원소를 나머지 원소와 비교하는데, 만약 그렇지 않다면 다른 원소를 나머지 원소와 비교한다. 이렇게 계속 비교해서 이 3가지의 원소를 크기 비교했을 때, 최종적으로 3!인 6가지 case가 나오게 된다.
트리의 깊이는 루트 노드(root node)부터 잎 노드(leaf node)까지의 가장 긴 경로로 이 경우에는 3일 것이다. 이는 정확히 알고리즘의 최악의 경우를 생각한 시간 복잡도이다. 즉, 최악의 경우 시간 복잡도는 트리의 깊이(depth)이다.
정렬 알고리즘을 트리로 나타내었을 때, 트리의 깊이는 최악의 경우가 되고, 해당 트리는 잎 노드를 n!개 가지게 된다. 그런데 이러한 트리의 잎 노드가 n!개를 가지려면 그 트리의 깊이는 log(n!)보다 더 작을 수 없게 된다. log(n!)를 수학적으로 증명하게 되면 다음 스털링(Stirling)의 공식을 통해서 Θ(nlogn)이 된다.
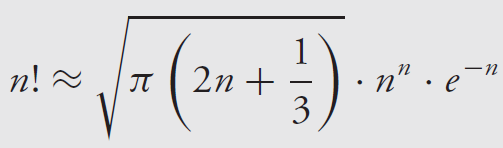따라서 어떠한 정렬 알고리즘이라도 트리의 높이가 Θ(nlogn)보다 낮을 수가 없게 된다. n개의 원소를 정렬하는 어떠한 트리도 최악의 경우에 Ω(nlogn)만큼 비교를 해야하고, 따라서 합병 정렬은 최적(optimal)이다.
