Dynamic programming에서 knapsack, 배낭 알고리즘은 대표적인 예시 중에 하나이다. 상황은 다음과 같다.
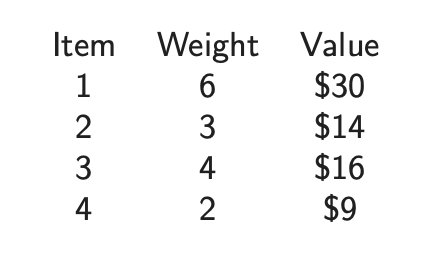우리는 가방을 하나 가지고 있다. 이 가방은 W = 10으로 모든 아이템의 무게가 10을 넘길 수 없다. 이러한 상황에서 최적의 조합을 어떻게 만들 수 있을까? 이때 최적의 조합이라는 것은 무게의 한도를 지키면서 값을 최대한 큰 것을 찾으면 된다. 이러한 문제를 knapsack 알고리즘이라 한다. 만약에 1번 아이템과 3번 아이템을 가져가게 되면 W = 10이기에 가능하며 이때 가격은 30 + 16 = 46이 된다. 다른 경우로 2, 3, 4번 아이템을 가져가게 되면 W = 9이기에 가능하며 이때의 가격은 14 + 16 + 9 = 39가 된다. 이렇게 가능한 경우들 중에서 최적의 조합을 찾아내야 한다.
간단한 예시로 아이템을 4개로 이야기했지만, 만약에 아이템의 각각이 개수가 무수히 많다고 가정하게 되면 어떻게 되겠는가? 이때는 가능한 경우가 굉장히 많아지고 쉽게 생각하기 어려울 것이다. 보통 이러한 문제는 greedy 알고리즘을 이용해서 풀면 효과적이긴하지만, 다음 code와 같이 dynamic programming으로도 풀 수가 있다.
이번에는 아이템 각각이 오로지 딱 한개씩만 존재한다면 어떻게 되겠는가? 이때도 dynamic programming 방법을 통해서 subproblem을 잘 구하면 된다.
이 경우에 대해서는 아이템을 가방에 챙길지 말지만 고민하면 된다. 만약 어떠한 아이템을 챙길 수 있다면 현재 무게가 그 아이템의 무게만큼 무거워지게 된다. 반대로 아이템을 가져가지 않을 수도 있는데, 이때는 현재 무게가 그대로 유지가 되면서 다음 아이템을 고려해야 한다. 결국, 아이템을 가져갈 경우와 가져가지 못할 경우 중에서 가장 큰 값이 우리가 원하는 답이 되는 것이다.
