이번에는 edit distance라고 해서 편집거리 알고리즘에 대해서 알아보려고 한다. 이는 두 문자열이 주어졌을 때, 두 문자열의 상호간의 유사도를 판단하는 알고리즘이다. 여기서 유사도를 판단한다는 것은 두 문자열이 같아지기 위해서 몇번의 추가(add), 편집(edit), 삭제(delete)가 이루어지는지 그 최소한의 횟수를 구하는 것이다. 다음의 예시를 통해서 두 문자열이 어느정도 유사한지 생각해볼까 한다.
위의 두 문자열 SNOWY와 SUNNY를 비교해보자. 그전에 먼저 용어 2개를 정의하고 갈 것이다. 먼저 cost라고 하는 것은 두 문자열을 비교할 때 동일한 위치에서 다른 문자열이 몇개가 존재하는지 개수를 나타낸 것이다. 가령 위에서 왼쪽과 같이 배열을 하게되면, S, N, Y는 동일한 위치에서 같은 문자를 나타내고 나머지 3개가 일치하지 않기 때문에 cost는 3이 된다. 오른쪽의 경우에는 N과 Y만 일치하고 나머지는 일치하지 않기 때문에 cost는 5가 될 것이다. 어떻게 배열하든지 상관없이 그 위치에 해당하는 문자가 같은지 다른지 개수만 따져주면 된다. 다음으로는 edit distance라는 것을 정의해보자. 두 문자열이 주어졌을 때, cost를 최소한으로 만드는 최적의 정렬이 존재하게 될텐데, 이때의 cost값을 말한다.
우리는 지금 dynamic programming 문제들을 접근하고 있다. Edit distance 역시 dynamic programming 방법으로 풀 수가 있다. 그렇다면 이 문제를 어떻게 sub problem으로 만들어서 효율적으로 풀 수 있을까?
먼저 두 문자열 x와 y를 정의해보자. x는 m개의 문자로 만들어진 문자열이고 y는 n개의 문자로 만들어진 문자열이라 하자. 그러면 이 문자열들의 sub problem으로 부분 문자열을 만들 것이다. x는 m개보다 적은 i개, y는 n개보다 적은 j개의 문자로 부분 문자열을 만들 것이다. 그리고 우리는 E(i,j)라고 해서 x 문자열의 시작 부분부터 i번째 부분까지, y 문자열의 시작 부분부터 j번째 부분까지 변환시키는 edit distance라고 정의할 것이다. 위의 예시에서 SNOWY와 SUNNY를 예시로 E(4,3)은 SNOW를 SUN으로 변환시키는데 필요한 edit distance이다. 그러면 E(5,5)는 SNOWY를 SUNNY로 변환시키는데 필요한 edit distance가 된다.
그리고 E(i,j)는 위의 점화식과 같이 3가지의 경우에 대해서 최소값으로 값이 기록이 될텐데, 점화식을 자세히보면 보통 저러한 형태는 테이블로 표현하면 더욱 쉽게 이해할 수 있다. 그래서 우리는 이에 대해서 테이블로 예시를 들어가면서 값을 기록해볼 것이다.
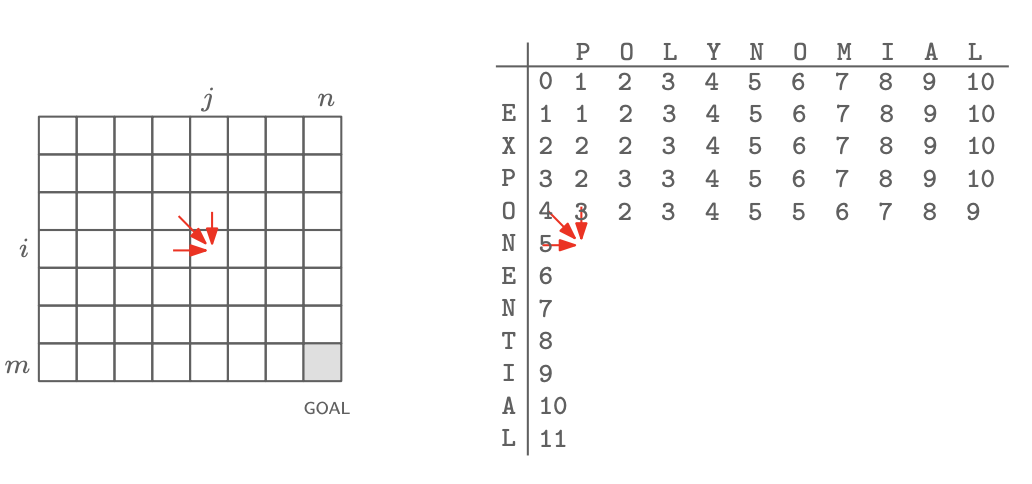테이블에서 0은 빈 공백을 나타내고, 테이블에 적을 수 있는 수는 3가지 경우가 나올 수 있다. 세번째 경우에서 diff(i,j)를 하게 되는데, 첫번째 문자열의 i번째 문자와 두번째 문자열의 j번째 문자가 같은 경우에는 0, 다른 경우에는 1이 된다. 그리고 이를 code로 표현하면 다음과 같다.
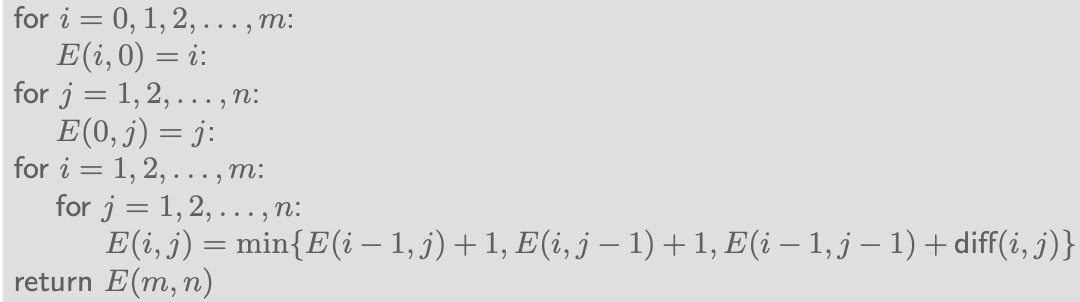이렇게 edit distance를 dynamic programming으로 구하게 되면 시간 복잡도는 O(mn)이 된다. 그냥 두 문자열의 길이를 곱한 수가 될텐데, 그 이유가 테이블이 m과 n을 곱한 크기로 만들게 되는데 값을 채워가서 우리가 원하는 최소값을 찾기만 하면 되기 때문에 이 과정은 O(1)이 된다. 그렇기 때문에 종합적으로 O(mn)이 되는 것이다.
