.png)
Dynamic Programming
Dynamic Programming(DP)는 일종의 점화식을 세울 수 있는 문제들을 풀 때 유용한 알고리즘이다. 우리가 풀고자 하는 문제를 하위 문제들로 나누어 작은 문제들을 푼 다음에 이를 이용하여 점점 상위 문제들을 풀어나가는 것이다. 점점 풀어나가면서 이전의 답이 이후의 문제의 힌트가 되어 직접적으로 도움이 되기에 굉장히 효율적이다.
Longest Increasing Subsequences(LIS)
Longest Increasing Subsequences(LIS) 문제는 원소가 n개인 배열에서 일부 원소들을 골라내어 만든 부분 수열 중에서 이전 원소보다 크다는 조건을 만족하고 그 길이가 최대인 부분 수열을 찾아야 한다. 그래서 input으로는 숫자들을, ouput으로는 이 숫자들을 중에서 가장 많이 증가하는 부분 수열이 된다. 그리고 이때 우리는 DP를 사용해서 문제를 간단하게 풀 것이다.
예시를 통해서 문제를 풀어보도록 하자. 적당히 {5, 2, 8, 6, 3, 6, 9, 7} 이라는 input이 있다. 그리고 이를 다음과 같이 일종의 그래프처럼 나타내고 싶다.
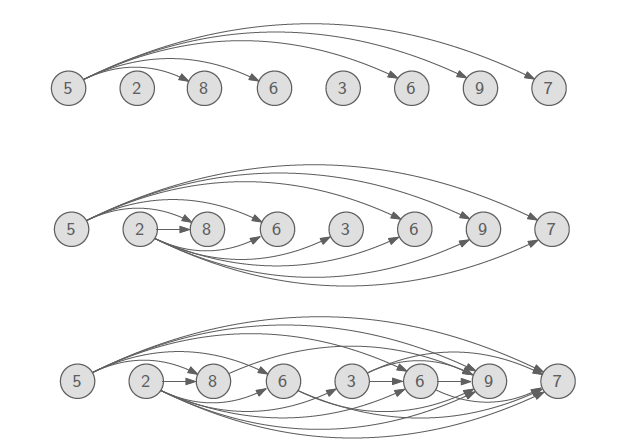그러면 이 왼쪽부터 현재 숫자보다 큰 숫자들을 전부 화살표로 이어준다. 이렇게 봤을 때, 이 문제가 왜 DP인지 궁금할 것이다. 각각의 숫자를 node라고 생각했을 때, 이 숫자보다 큰 숫자를 전부 연결하는 과정 속에서 총 8개의 원소를 확인해야 하기에 8번의 node를 확인해야 한다. 그러면 우리는 LIS를 찾기 위해서 8개의 하위 문제를 풀면서 이를 기반으로 진행하고 싶은 것이다. 어떻게 하고 싶은지 다음의 점화식을 한 번 보도록 하자.
답부터 이야기하면 이 수열의 LIS는 4일 것이다. 그리고 이는 {2, 3, 6, 9} 혹은 {2, 3, 6, 7}에 해당할 것이다. 우리가 원하는 것은 어떠한 숫자들의 구성이 아니라 오로지 길이이다. 그래서 첫번째 원소부터 마지막 원소까지 하나의 비교 대상으로 설정해놓고, 첫번째 원소부터 자기 자신까지 순회를 하면서 크기를 비교하여 DP라는 배열의 값의 증가 추세를 확인하는 것이다.
LIS Running time
n개의 원소가 주어진다면, LIS를 구하기 위해서 max 값을 업데이트 하는데 n의 제곱만큼 2중 반복문을 돌아야한다. 그래프의 관점으로는 n개의 node에 대해서 최대한으로 n의 제곱만큼의 edge를 확인해야하는 것인 셈이다. 하지만 이러한 시간 복잡도는 오랜 시간이 걸리게 된다. LIS를 구하는데 있어 binary search를 하게 되면 이러한 시간 복잡도를 O(nlogn)까지 줄일 수 있다. 사실 시간 복잡도가 더 좋은 쪽으로 하는 것이 효율적이겠지만, 여기서는 dynamic programming이 어떻게 적용되는지가 더 중요하다.
