무방향 그래프(Undirected Graph)
무방향 그래프(Undirected Graph)는 보통 G = (V, E)로 표현된다. 여기서 V는 정점(Node)을 이야기하고, E는 정점들을 연결하는 간선(EdgE)를 말한다. 무방향 그래프의 특징은 이 간선들이 방향이 없다는 것이다. 즉, 정점들 사이에 정해진 방향은 없는 셈이다.
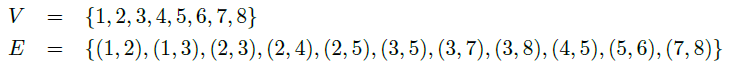예를 들어, 위와 같이 V와 E가 정의가 된다면, 그래프는 다음과 같이 그릴 수 있다.
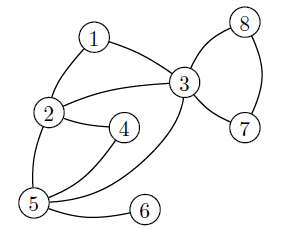혹은 반대로 그래프가 주어졌을 때, V와 E를 집합 형식으로 표현할 수 있다. 어느것이 맞다 틀리다가 아니라 그래프를 표현하는 방법은 위와 같이 존재할 수 있는 것이다.
인접 행렬(Adjacency Matrix)
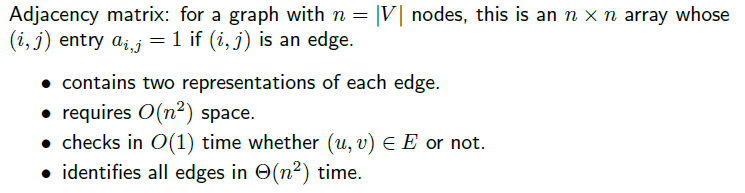
그래프를 표현하는 또 다른 방법으로 인접 행렬(Adjacency Matrix)가 있다. 인접 행렬은 n * n 행렬로, 각각은 i번째 행과 j번째 열이 0과 1로 나타냄으로써 그 의미가 그래프와 동일해질 수 있다. 만약 i번째 정점과 j번째 정점이 간선으로 연결되어 있다면, 해당하는 곳에는 1이 적히는 것이다. 반대로 간선이 존재하지 않는다면 0이 적힐 것이다. 무방향 그래프이기 때문에 인접 행렬은 대각선을 기준으로 대칭일 것이다. 예를 들어 다음의 왼쪽의 그래프를 통해서, 이 그래프를 행렬로 표현할 수 있다.
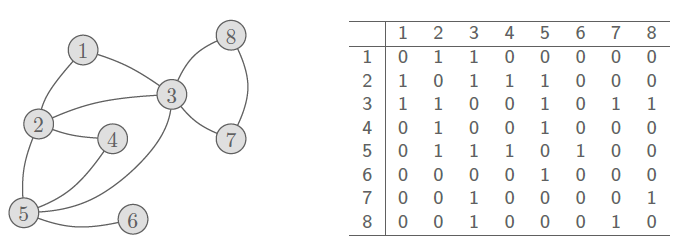인접 행렬은 정점 i와 j가 연결되어 있는지 확인하고 싶으면, 해당하는 칸의 값이 0인지 1인지만 확인하면 되기 때문에 O(1)의 시간 복잡도에 확인할 수 있다. 하지만, 특정 정점 i에 연결된 모든 정점들을 방문하고 싶을 때는 해당 i행의 모든 열을 확인해야 하기 때문에 O(n)의 시간 복잡도가 걸린다. 즉, 모든 정점을 확인하기 위해서는 n의 제곱만큼의 시간 복잡도가 필요한 것이다.
인접 리스트(Adjacency List)
그래프를 표현하는 또 다른 방법으로는 입접 리스트(Adjacency List)가 있다. 인접 행렬이 행렬로 그래프를 표현한 것이라면, 인접 리스트는 리스트로 그래프를 표현한 것이다. 그 중에서도 링크드 리스트(Linked List)로 표현이 되는데, 이 링크드 리스트는 무방향 그래프를 나타내야 하기 때문에 서로 반대 방향을 모두 연결시켜야 한다. 그래서 다음 그래프와 리스트를 살펴보면 1이 2와 연결되어 있는 것을 2에서 1로 연결되도록 중복해서 적은 것을 볼 수 있다.
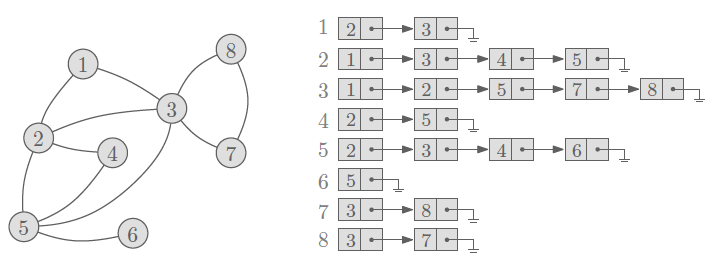인접 리스트는 인접 행렬과 달리, 실제로 연결된 정점들에 대한 정보만을 갖고 있기 때문에, 모든 방향선의 원소 개수의 합이 간선의 개수와 같다는 점이다. 예를 들어, 정점 2와 연결된 모든 정점을 방문하고 싶다면, 인접 행렬의 경우 총 7번을 확인해야 하지만, 인접 리스트의 경우 실제 연결된 정점만 확인하면 되기에 4번만 확인하면 된다.
모든 정점을 확인한다고 했을 때, 인접 리스트는 각 정점마다 연결된 정점만 확인하는 것이 가능하기에, 전체 간선의 개수와 정점만 확인하면 된다. 따라서 정점의 개수 + 간선의 개수만큼의 시간 복잡도만 필요한 것이다.
