경로(Path)
그래프에서 경로(Path)란 서로 연결되어 있는 간선 혹은 정점들을 순서대로 나열한 것을 말한다. 일반적으로 그래프의 경로는 단순(Simple) 경로를 말하는데, 여기서 단순하다는 것은 정점을 단 한번만 지나가는 경로를 말한다. 아래 그림에서 예를 들면, "1245"가 하나의 단순 경로가 될 수 있다. 일반적으로 알고리즘 문제를 해결하는 과정에서 문제 상황이 그래프로 판단이 된다면, 최적의 경로를 찾게되면 그 문제의 해답이 나올 것이다.
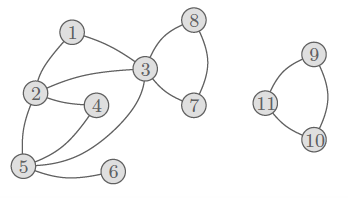
사이클(Cycle)
그래프에서 사이클(Cycle)이란 어떤 특정 정점에서 출발하여 간선과 정점들을 지나 다시 처음에 출발했던 특정 정점으로 되돌아오는 것을 말한다. 위의 그림을 예로 들면, 만약 3에서 출발하게 된다면 "3783"을 하나의 사이클로 판단할 수 있을 것이다.
연결성(Connectivity)
그래프에서 연결성(Connectivity)는 주어진 무방향 그래프에서 모든 정점들의 쌍에 대해서 어떻게든 경로가 존재함을 의미한다.
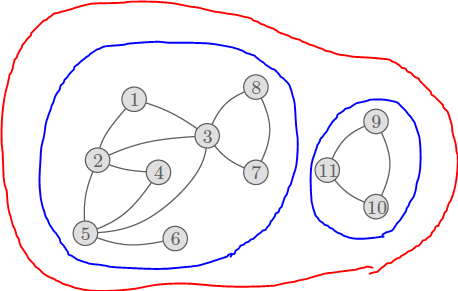위의 그림에서 파란색으로 이어진 그래프들은 연결되었다고 볼 수 있지만, 빨간색으로 이어진 그래프를 보면 중간에 이어진 간선이 없어 좌측 그래프에서 우측 그래프로 어떻게 해도 갈 수가 없기에, 이는 연결되지 않았다고 할 수 있다..
트리(Tree)
트리(Tree)는 정의대로 하면 연결되어 있고(Connected) 순환하지 않은(Acyclic) 무방향 그래프를 말한다. 순환하지 않다는 것은 사이클이 없다는 말과 의미가 같다. 즉, 트리는 연결되어 있지만, 사이클은 없는 그래프를 말한다.
여기 G라는 그래프가 있다고 하면, 위에서 2가지만 만족하면 나머지 하나는 자연스럽게 만족하게 된다. 예를 들어, (a)와 (b)가 만족해서 G가 연결되어 있지만, 사이클이 없다면 G는 자연스럽게 n - 1개의 간선을 가지게 되는 것이다. 다른 예로, (b)와 (c)를 만족해서 G가 사이클이 없고, n - 1개의 간선을 가지게 된다면 G는 자연스럽게 연결되어 있는 것이다.
그리고 트리의 성질 중에 만약 무방향 그래프가 트리라면 어떠한 정점들 쌍 사이의 단 하나의 경로가 존재한다가 성립한다. 이는 역도 성립하는데, 이를 증명하면 다음과 같다.
- 만약에 트리라면, 어떠한 두개의 정점들 사이에는 오직 하나의 경로가 존재할 것이다. 만약 간선이 더 많다면 이는 곧 사이클을 형성하게 될 것인데, 트리의 정의상 사이클은 존재하면 안된다. 그래서 인접한 정점과 정점 사이에는 단 하나의 간선만 존재할 수 있고, 거리가 먼 정점 사이에는 하나의 경로만 존재하게 되는 것이다.
- 반대 경우는 정점들 사이에 하나의 경로가 존재한다는 것은 이 그래프가 자연스럽게 연결되어 있다는 것이다. 경로가 존재한다는 것은 그 정점으로 갈 수 있다는 것을 의미하고, 이는 연결되어 있음이 보장되어 있다. 그래서 정점들 사이의 경로는 하나로 정해지면서 사이클은 형성될 수 없기 때문에, 정의상 이 그래프는 트리가 되는 것이다.
