Disjoint Set
Disjoint Set이란 서로 중복되지 않는 부분들로 나눠진 원소들에 대한 정보를 저장하고 사용할 수 있는 자료 구조이다. 즉, 두 집합이 서로 서로소인 셈이다. 이러한 자료 구조는 집합의 일종이기 때문에 array나 linked list와 같은 자료 구조를 사용할 수도 있는데, 가장 효율적인 tree를 사용할 것이다. 그리고 이러한 disjoint set을 유지하고 표현하기 위해서는 일종의 알고리즘이 필요한데, 이러한 알고리즘을 Union and Find라고 한다.
Union and Find Function
Union and Find를 정의하기 위해서는 다음의 3가지 연산을 정의해야 한다. 하나씩 살펴보면 다음고 같다.
1. makeset(x): 이 단계는 초기화 하는 단계로, x를 포함하는 새로운 집합을 만든다.
2. find(x): 이 단계는 찾는 단계로, x가 포함이 된 집합에서의 root node를 반환한다. 그 이유는 x가 어떤 집합에 속해 있는지 판단하고 싶은데, 이때 그 집합을 대표할 수 있는 것이 root node이기 때문이다.
3. union(x, y): 이 단계를 합치는 단계로, x와 y가 포함이 된 각각의 집합을 합쳐서 새로운 집합을 만든다.
그리고 node x에 대해서 다음의 함수도 약속해둔 뒤 알고리즘이 어떻게 동작하는지 살펴보도록 할 것이다.
1. π(x): 이 함수는 x의 parent node를 가리키는 pointer이다.
2. rank(x): 이 함수는 x가 가지고 있는 subtree의 hieght를 가리킨다.
Union and Find Algorithm
위에서 설명한 makeset, find, union을 code로 나타낸 것이다. 여기서의 핵심은 rank 값의 비교를 통해서 두 집합을 union하는 것이다. 크게 어렵지 않으니 천천히 읽어보면 될 것이다.
Union and Find Example
실제로 어떻게 돌아가는지 간단한 예시를 통해서 살펴보려고 한다.
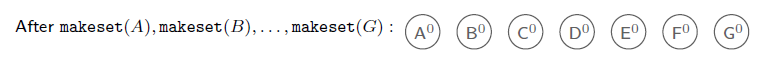첫번째로는 A부터 G까지의 node를 이용해서 서로 독립적인 set을 만드는 것이다. 이때 각 set의 rank값은 전부 0이 될 것이다.
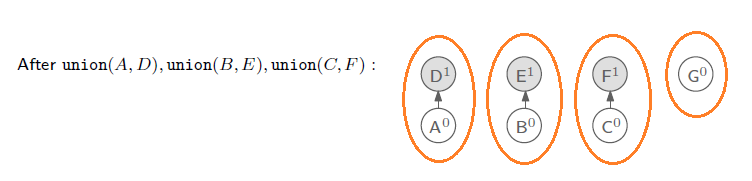다음으로는 union 함수를 이용해서 A와 D, B와 E, C와 F를 하나의 set으로 합쳐보았다. 함수대로 y가 x의 rank값이 같다면 y가 x의 parent node가 되어야 하기 때문에 D, E, F를 각각 A, B, C의 parent node로 연결해준 다음에 rank 값을 업데이트 시켜주면 된다.
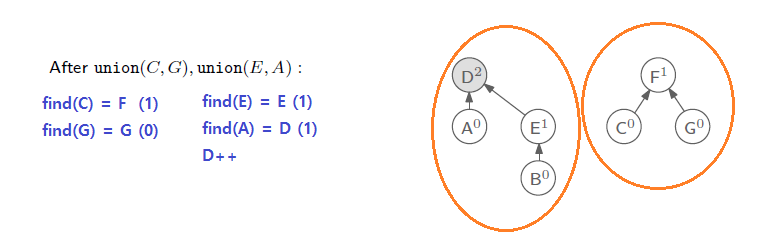다음으로는 C와 G, E와 A를 합칠 것이다. 여기서 find(C)는 F로 rank 값이 1이 되며, find(G)는 G 자신으로 rank 값이 0이 되어 rank 값이 큰 C가 G의 parent node가 되어야 한다. 이렇게 새로운 set을 만들고 다음 union에서 find(E)는 E 자신으로 rank 값이 1이며, find(A)는 A의 root node인 D가 되어 rank 값이 이 또한 1이 된다. 그래서 rank 값이 같기 때문에 D가 E의 parent가 되어야 한다. 그 뒤에는 D의 rank 값을 업데이트 해주면 된다.
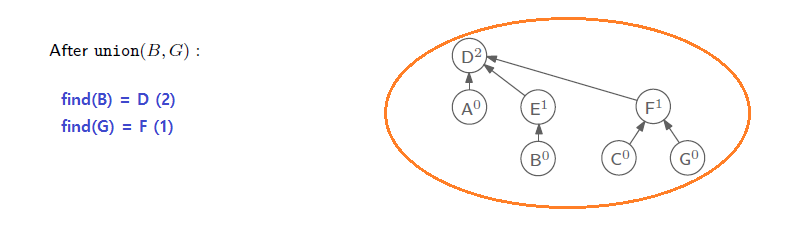마지막으로는 B와 G를 합칠 것이다. B의 root node는 D이고, G의 root node는 F이다. 그래서 rank 값이 2와 1이 되기 때문에 D가 F의 parent node가 되면 된다. 그래서 최종적으로는 union and find 알고리즘을 통해서 하나의 set을 만든 것을 볼 수 있다.
Union and Find Properties
Union and Find 알고리즘의 몇가지 성질을 간단하게만 알아보고 넘어가도록 할 것이다.
- 어떤 node x에 대해서 rank 값은 자신의 subtree의 height 값이기 때문에 x 자신의 rank값은 x의 root node의 rank 값보다 작거나 같아야 한다. 같은 경우는 아무래도 자기 자신이 root인 경우일 것이다.
- 만약 node x에 대해서 root가 아닌 경우에는 rank 값이 바뀌지 않는다. 알고리즘을 보면 알겠지만, 처음에 root node를 찾은 후에 root node의 rank 값만 업데이트하기 때문에 non-root node의 rank 값은 바뀔 수가 없다.
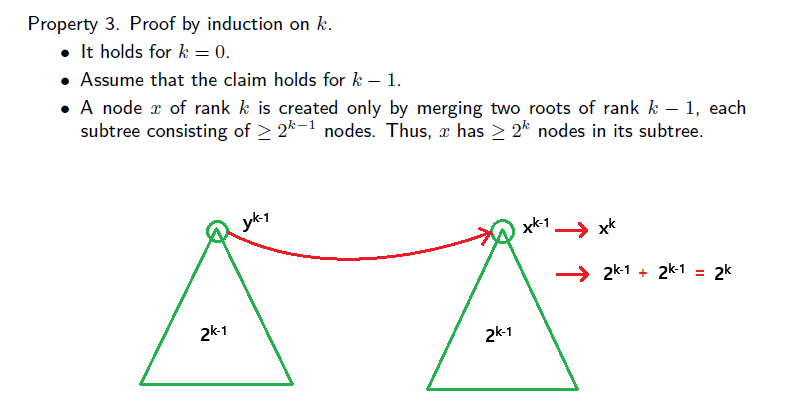
- k값을 rank로 가지는 root node는 적어도 2의 k제곱만큼의 node를 자신의 tree에 존재할 것이다. 이는 간단한 증명을 통해서 확인해 볼 것이다.
- 전체가 n개의 node가 존재할 때, rank k의 값은 n을 2의 k제곱을 나눈 값을 넘어갈 수 없다. Tree에 대해서 잘 알고 있다면, rank의 최대값은 log n이 될 것이다. 따라서 모든 tree의 height는 log n을 넘어갈 수 없고, 이는 union and find의 running time의 upper bound이다.
