Directed Acyclic Graph
Directed acyclic graph(DAG)는 이름에서부터 우선 방향성이 있어야하며, acyclic 해야한다. 여기서 cyclic이라는 것은 그래프 상에 cycle이 존재하지 않는다는 이야기이다. 즉, 어느 한 지점에서 출발하였을 경우에 다시 그 지점으로 돌아올 수 없다.
Topological Ordering
Topological ordering은 위상 정렬이라해서 방향성이 있는 그래프에서 node들이 방향을 거스르지 않게 정렬하는 것을 말한다. 이 그래프 상에서 edge를 e = (u, v)라고 할 때, u에서 출발하여 v로 도착하는 edge들에 대해서 u는 반드시 v보다 먼저 등장해야 하는 것이다.
모든 DAG는 적어도 incoming edge가 없는 node가 존재한다. Topological ordering은 outgoing edge들과 함께 해당 incoming edge가 없는 node를 되풀이하면서 제거를 하게 된다. 이러한 과정 속에서 DAG가 topological ordering을 진행하게 되는데, 결국 정리해서 이야기하면 directed 그래프가 DAG가 되기 위해서는 이 그래프가 topological ordering을 가져야하며, 반대로 topological ordering을 가지는 그래프는 DAG가 된다. 그러면 다음의 예시를 통해서 이 그래프가 topological ordering을 가지는지 알고리즘을 통해서 확인해보겠다.
Topological Ordering Example
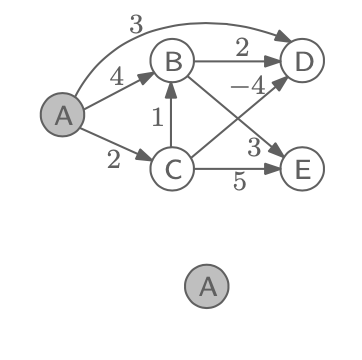먼저 방향이 존재하는 그래프에서 incoming edge가 없는 A node를 먼저 가장 왼쪽에 둘 것이다.
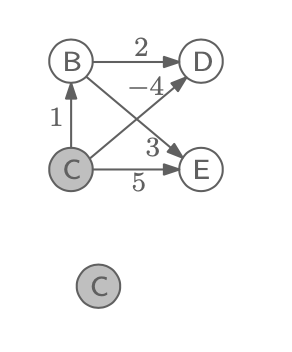그 후 A를 임의로 지운 후에 다시 incoming edge가 없는 C를 두번째로 둘 것이다.
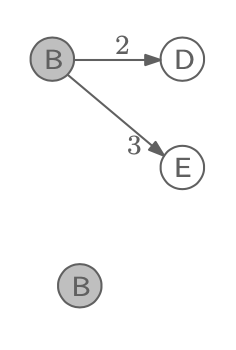같은 방식으로 C를 지우고 B를 세번째로 둘 것이다.
남은 D와 E 중에서는 아무거나 네번째, 다섯번째로 두어 다음과 같이 순서대로 정렬한다.
이렇게 정렬을 하게 되면 왼쪽에서부터 오른쪽으로 방향성이 일관되게 정렬이 되며, 이 그래프는 따라서 DAG를 만족하게 된다.
DAG Shortest Path
위에서 그래프가 DAG를 만족하려면 topological ordering을 가져야만 한다고 이야기 했다. 우리는 지금부터는 DAG로 부터 만들어진 topological ordering을 통해서 shortest path를 찾을 것이다. 우선 이를 행하기 위해서 다음과 같은 code를 통해서 알고리즘이 어떻게 진행되는지 확인해보자.
알고리즘의 초반부는 다익스트라 알고리즘과 마찬가지로 모든 node에 dist 값을 무한대로 설정해주고 시작지점의 node는 dist를 0으로부터 진행한다. 중간에 Linearize라는 함수 속에 또다른 함수가 존재하는데, 이 함수는 그냥 topological ordering이라고 생각하면 된다. 우리는 그래서 topological ordering을 만들어놓고 shortest path를 찾을 것이다.
먼저 모든 edge에 대해서 dist 값을 초기화 해준다. 시작지점은 당연히 왼쪽부터이며, dist값을 비교해가면서 더 작은 값으로 업데이트하는 것이 이제부터 할 작업이다.
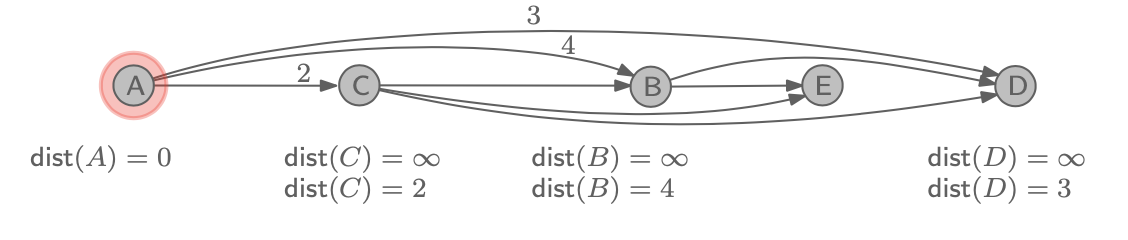A는 B, C, D로 outgoing edge를 가지고 있기 때문에, 먼저 B, C, D의 dist 값을 업데이트 해준다. 당연히 처음 단계이기 때문에 무한대보다는 작은 값을 가지고 있어 바로 업데이트가 가능하다.
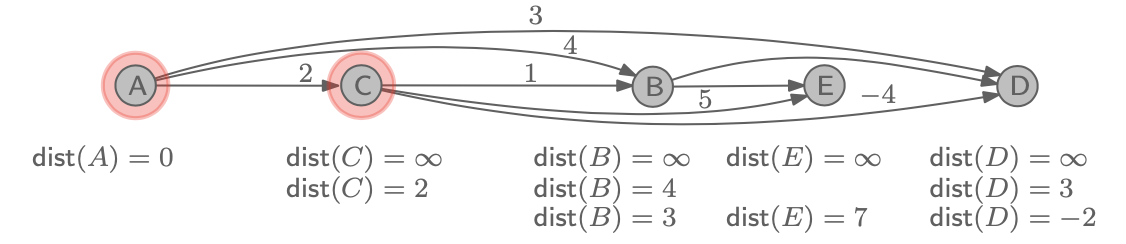A가 끝났으면, 바로 오른쪽의 C로 향해서 진행하는데, C는 B, D, E로 향하는 edge를 가지고 있다. 그래서 dist(C)와 이 edge들의 정수 값을 합쳤을 때, 이 값이 기존의 dist보다 작으면 업데이트하고 아니면 그냥 냅두면 된다.
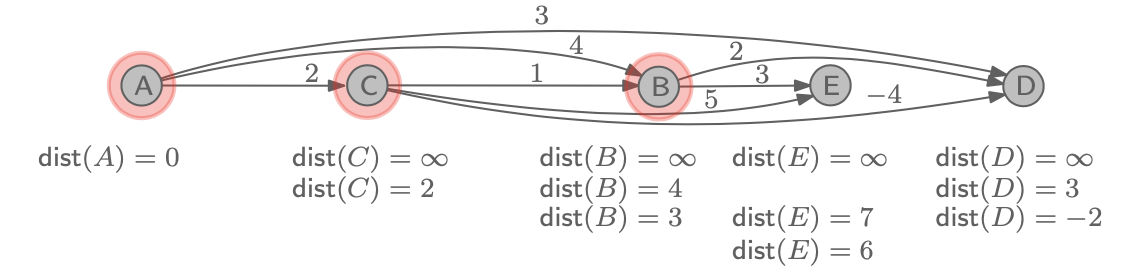마찬가지로 똑같이 진행해주면 된다.
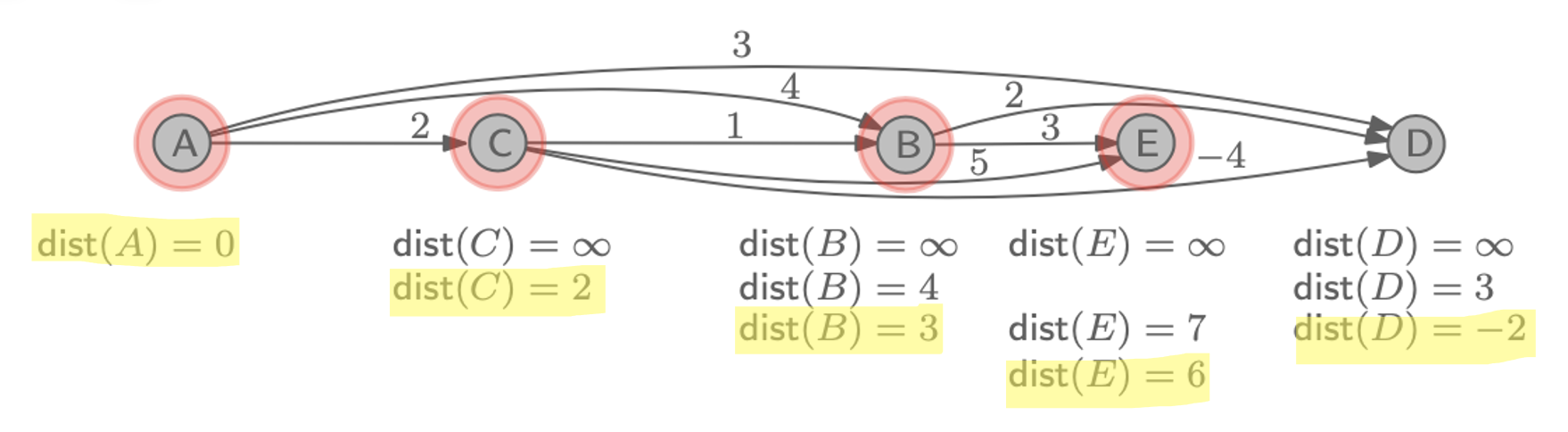더이상 진행이 안되었을 때, 마지막으로 남아있는 dist 값들이 A로 부터의 shortest path가 되는 것이다.
