[Transformer]#1 Attention

Attention class

init method

class SelfAttention(nn.Module):
  def __init__(self, input_size, hidden_size, num_head, mask_value=0):
    super().__init__()
    self.input_size = input_size
    self.hidden_size = hidden_size
    self.qkv = nn.Linear(self.input_size, self.hidden_size * 3)
    self.out_proj = nn.Linear(self.hidden_size, self.input_size)
    self.mask_value = mask_value
    self.num_head = num_head
    assert self.hidden_size % self.num_head == 0
    self.dim_per_head = self.hidden_size // self.num_head

forward method

this method can be divided into two parts
1st : getting QKV vectors from a given input vectors
2nd : calculating attention values from QKV

forward method of self_attention

  def forward(self, x, mask=None):
    if mask is None:
      mask = torch.ones([x.shape[0], x.shape[1], x.shape[1]])

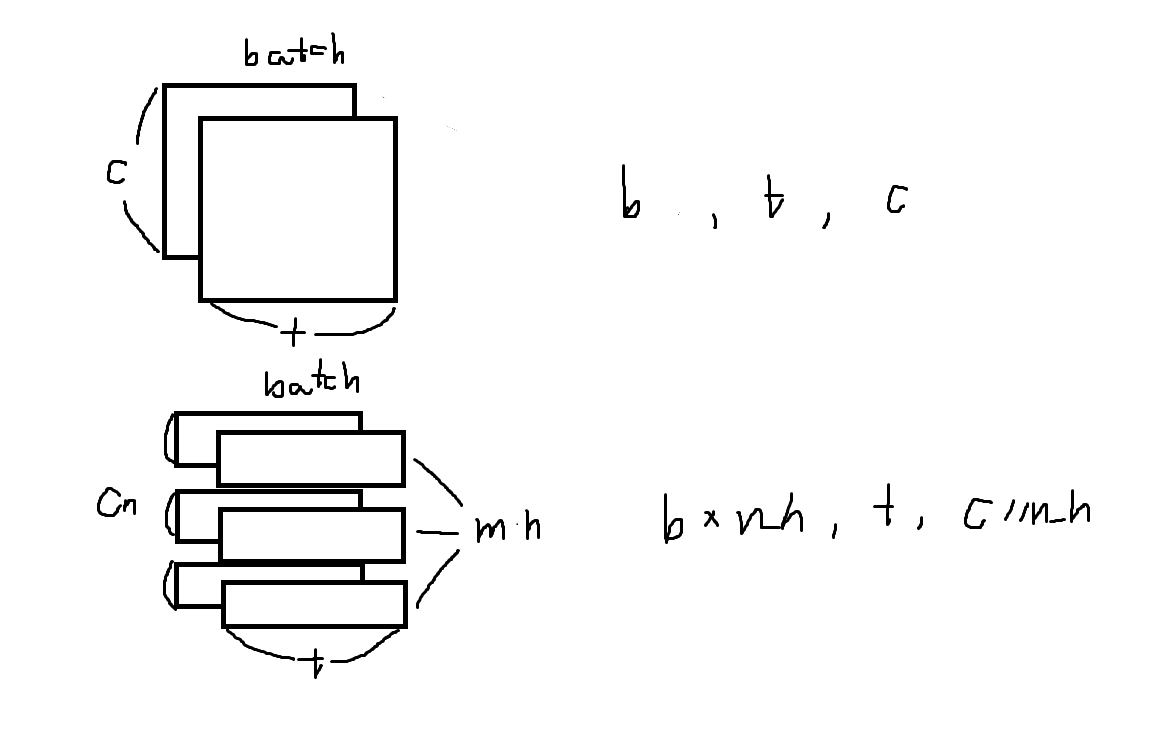
    head_repeated_mask = mask.unsqueeze(1).repeat(1, self.num_head, 1, 1).reshape(-1, mask.shape[1], mask.shape[2]) # [N * num_head, T, T]
    queries, keys, values = self._get_qkv(x) # [N, T, Cn]
    queries = self._get_multihead_split(queries) # [N * num_head, T, Cn // num_head]
    keys = self._get_multihead_split(keys)
    values = self._get_multihead_split(values)

    att_score = self._get_multiheaded_att_score(keys, queries)
    att_score /= keys.shape[-1] ** 0.5
    att_weight = self._get_masked_softmax(att_score, head_repeated_mask) # [N * num_head, T, T]
    value_with_att = self._get_weighted_sum(values, att_weight) # [N * num_head, T, Cn // num_head]
    value_with_att = self._get_multihead_concat(value_with_att) # [N, T, Cn]
    output = self.out_proj(value_with_att) # [N, T, C]

    return output

forward method of cross_attention

  def forward(self, q_seq, kv_seq, mask=None):
    '''
    Arguments:
      q_seq (torch.Tensor): Sequence to be used for query
      kv_seq (torch.Tensor): Sequence to be used for key and value
      mask (torch.Tensor): Masking tensor. If the mask value is 0, the attention weight has to be zero. Shape: [N, Ty, Tx]

    Outs:
      output (torch.Tensor): Output of cross attention. Shape: [N, Tx, C]
    '''
    if mask is None:
      mask = torch.ones([q_seq.shape[0], kv_seq.shape[1], q_seq.shape[1]])

    # get cross attention score
    head_repeated_mask = mask.unsqueeze(1).repeat(1, self.num_head, 1, 1).reshape(-1, mask.shape[1], mask.shape[2]) # [N * num_head, T, T]
    queries, _, _ = self._get_qkv(q_seq) # [N, T, Cn]
    queries = self._get_multihead_split(queries) # [N * num_head, T, Cn // num_head]
    _, keys, values = self._get_qkv(kv_seq) # [N, T, Cn]
    keys = self._get_multihead_split(keys) # [N * num_head, T, Cn // num_head]
    values = self._get_multihead_split(values) # [N * num_head, T, Cn // num_head]

    att_score = self._get_multiheaded_att_score(keys, queries)
    att_score /= keys.shape[-1] ** 0.5
    att_weight = self._get_masked_softmax(att_score, head_repeated_mask) # [N * num_head, T, T]
    value_with_att = self._get_weighted_sum(values, att_weight) # [N * num_head, T, Cn // num_head]
    value_with_att = self._get_multihead_concat(value_with_att) # [N, T, Cn]
    output = self.out_proj(value_with_att) # [N, T, C]

    return output

1st step : getting QKV vectors from a given input vectors

example of total splitting made for self-attention

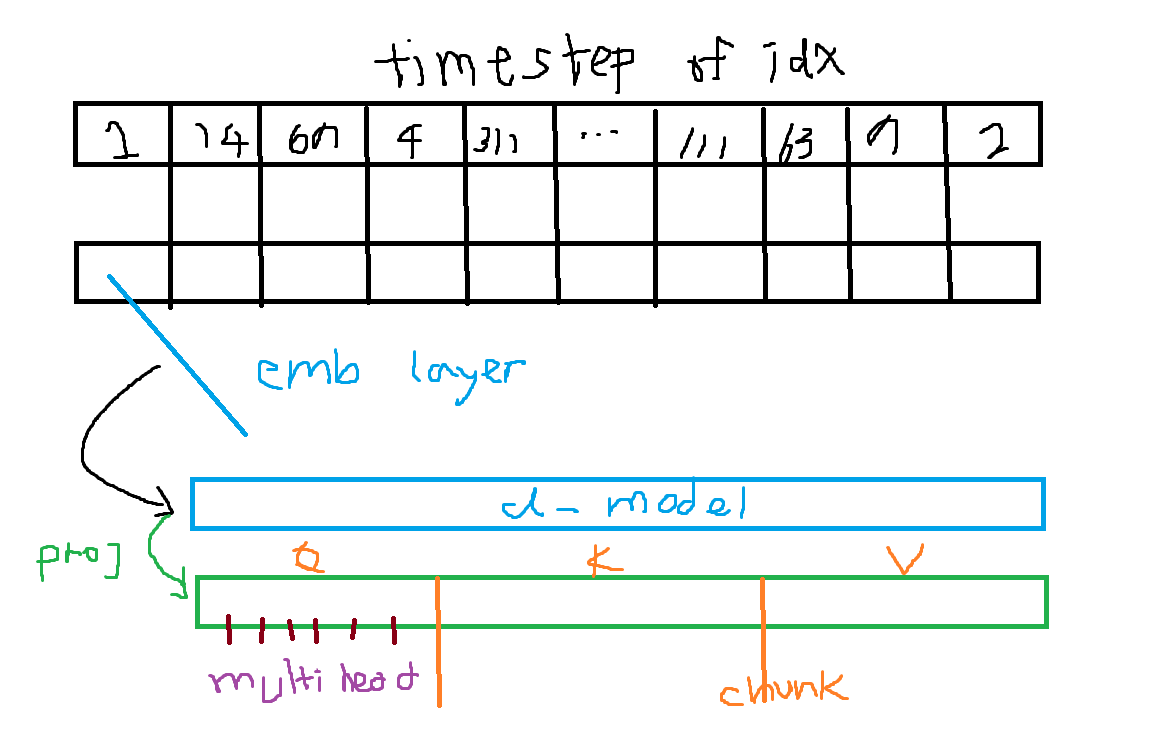
how multi-head splitting works

remember! batch-wise + token-wise multiplication is proceeded so there are 1 on 1 matches between each queries and keys.
Indeed, when you split the input embeddings into multiple heads, each head will have a lower-dimensional representation (for example, 32 divided by 8 would result in 4 dimensions for each head). The key point here is that this lower-dimensional representation allows each head to focus on different aspects or perspectives of the input.

normalization

In high dimensional spaces, the dot product can have large or small values depending on the dimensionality. To mitigate the issue of extremely large or small values, we divide the dot product by the square root of the key dimension (the size of the key vector). This normalization step ensures that the attention scores remain stable and avoid overpowering other parts of the model, such as the softmax operation.

see the following cases

query : [1, 2, 3, 4, 5, 6]
key : [1, 2, 3, 4, 5, 6]

query_mh2 : [1, 2, 3], [4, 5, 6]
query_mh3 : [1, 2], [3, 4], [5, 6]

key_mh2 : [1, 2, 3], [4, 5, 6]
key_mh3 : [1, 2], [3, 4], [5, 6]

# normalized attention values
attention_mh2 : (1 + 4 + 9) / square_root(3)
attention_mh3 : (1 + 4) / square_root(2)

why normalization with square_root? not norm

1. Simplicity: Dividing by the square root of d_k is computationally simpler than computing the norm and normalizing with it.
2. Consistency: Normalizing with the square root of d_k provides a more consistent scaling effect. When using the norm, the scaling could change drastically depending on the specific values in the vector, while using the square root of d_k ensures a consistent scaling factor.
3. Improved Gradient Flow: Using the square root of d_k for normalization helps stabilize gradients by preventing overly large and small values in the dot products during training.

2nd step : calculating attention values from QKV

Query : [batch, timestep_q(tq), hidden_dimension(c)]
Key : [batch, timestep_k(tk), hidden_dimension(c)]
Value : [batch, timestep_k(tk), hidden_dimension(c)]
outputs : [batch, timestep_q(tq), hidden_dimension(c)]

So the outputs are tensors with weighted sum of key tensors with a certain question(word) from each timestep from query

1st getting attention score

Query x Key : torch.einsum('btqc, btkc -> btktq', Query, Key)

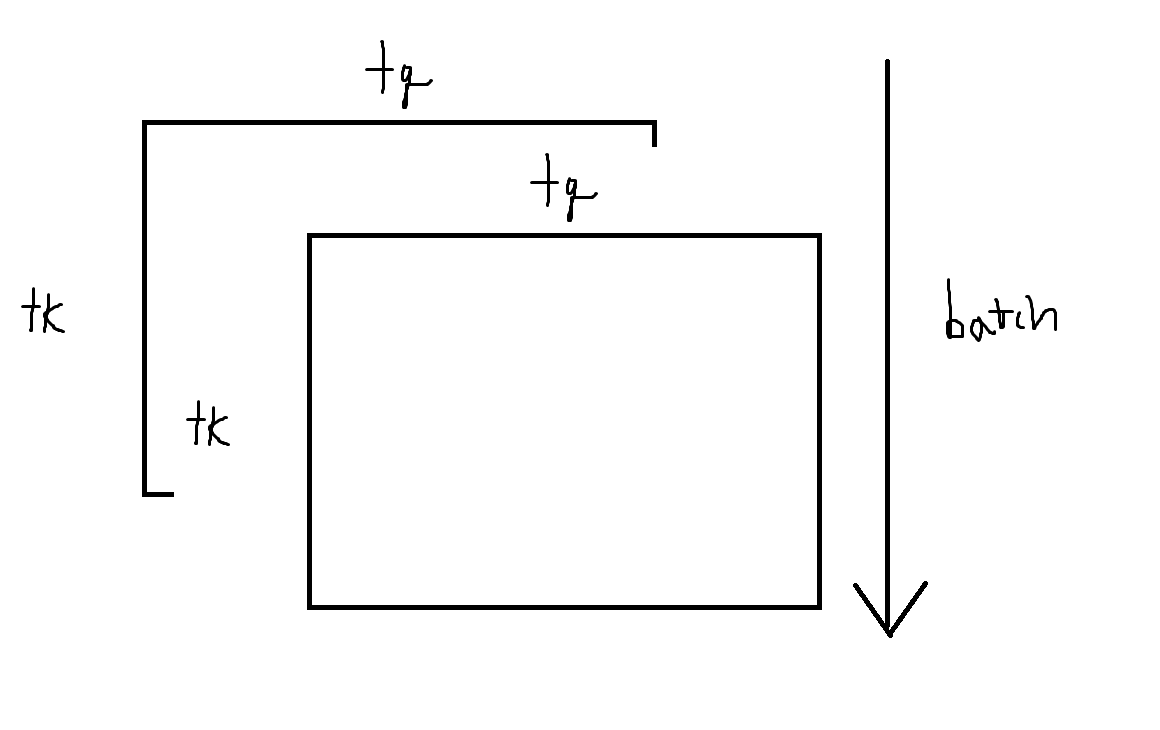
2nd getting attention weight

still "btktq" but applied with softmax in dimension 0(column)

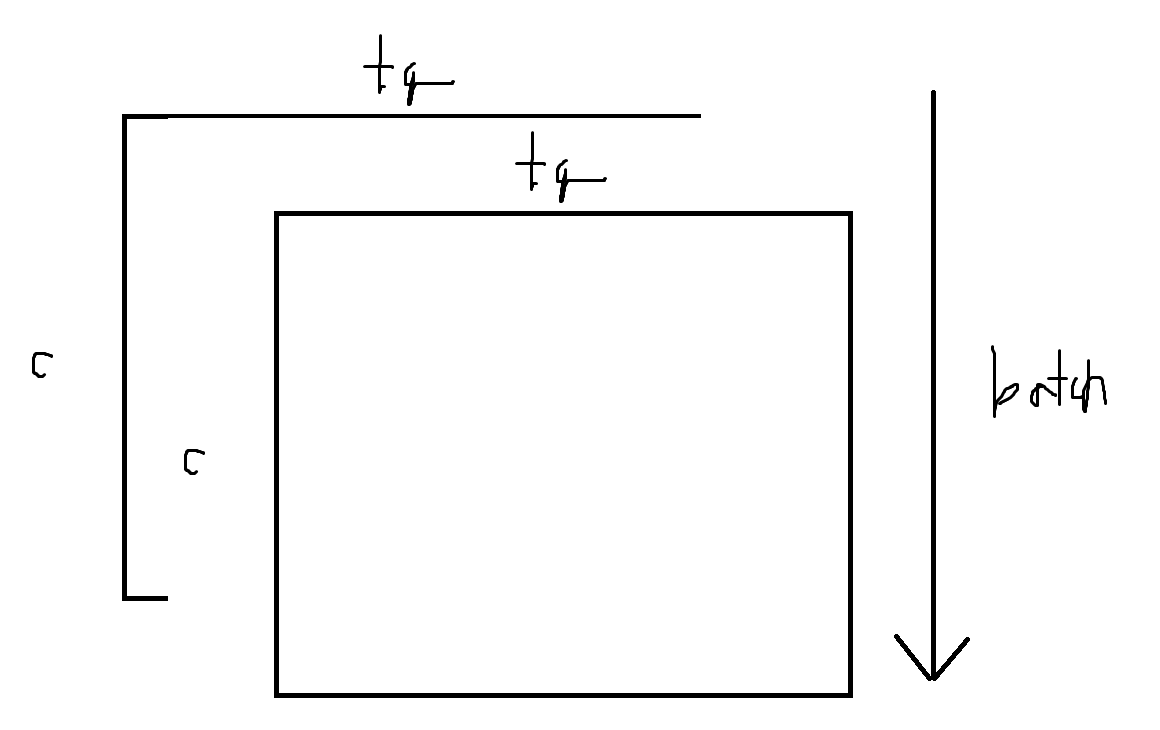
3rd weighted sum(summarization)

attention_score x Value : torch.einsum('btktq, btkc -> btqc', attention_score, Value)