[Sampling Method]#1 Eta-sampling feat.(Nucleus, Typical sampling)

All sampling codes expect the logits with shape of [batch x sequence_len x vocab_size] each batch and sequence_len is set to 1 in out case.

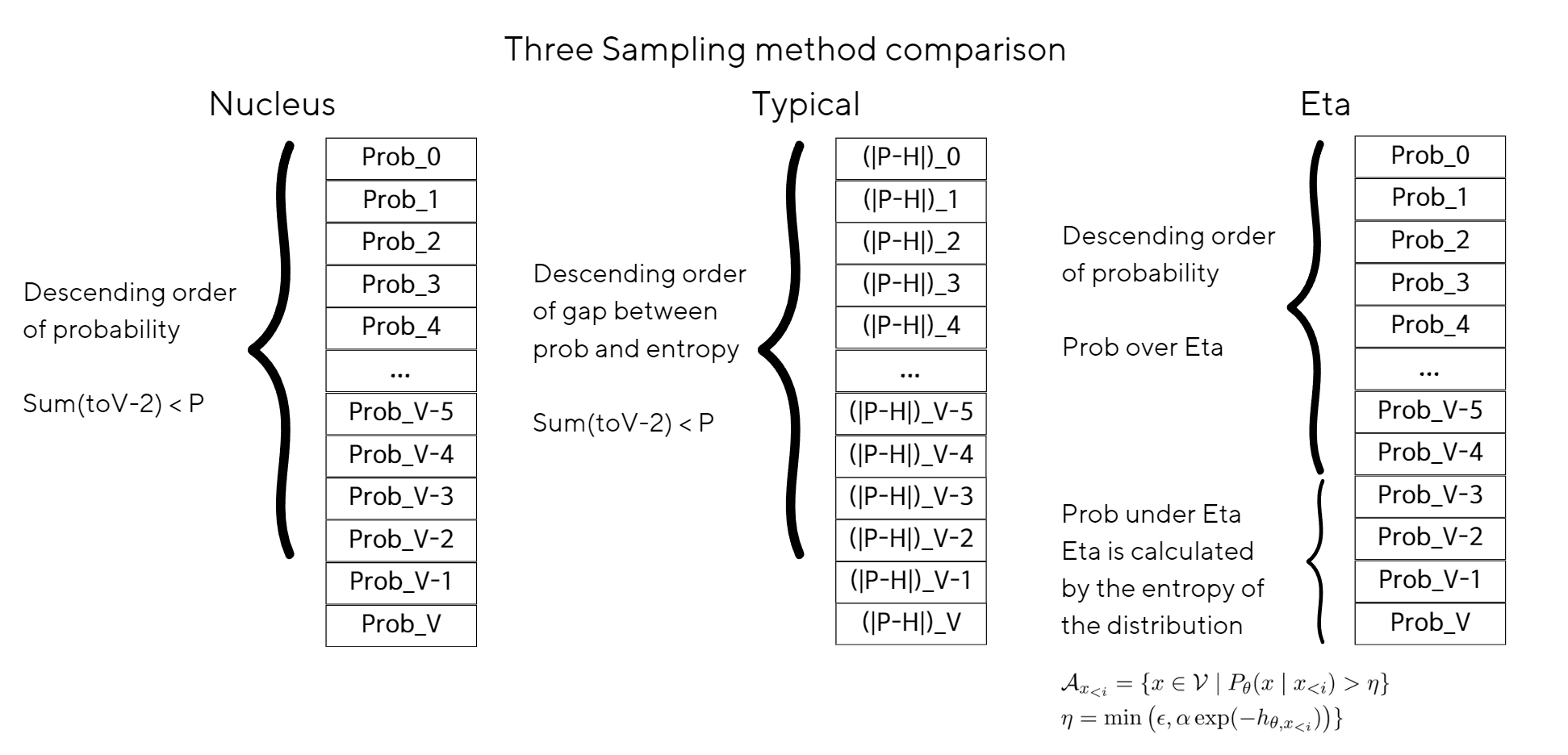
Eta-sampling

paper: https://arxiv.org/abs/2210.15191

The explanation provided describes an algorithm called η-sampling, which is designed to make decisions on which words to consider during the process of generating text, based on both the absolute and relative probability principles. To understand this, let's break down the key components and ideas:

Absolute Probability Principle:

This principle is about considering the actual probability values. For instance, an epsilon rule based on absolute probability might exclude words whose probabilities fall below a certain threshold (epsilon), irrespective of the distribution's characteristics.

Relative Probability Principle:

This principle considers the probability of words relative to the distribution's characteristics, such as its entropy. Entropy measures the uncertainty or disorder within a distribution; a higher entropy means more unpredictability.

code

# refered: https://github.com/john-hewitt/truncation-sampling
def eta_sampling(logits, epsilon) -> torch.FloatTensor:
  probabilities = logits.softmax(dim=-1)
  entropy = torch.distributions.Categorical(probs=probabilities).entropy()
  new_epsilon = min(epsilon, torch.sqrt(torch.tensor(epsilon))*torch.exp(-entropy))
  indices_to_remove = probabilities < new_epsilon
  max_word = torch.argmax(logits, dim=-1)
  indices_to_remove[..., max_word.squeeze()] = 0
  new_scores = logits.masked_fill(indices_to_remove, float("-inf"))
  return new_scores

Paper "EXPLORING SAMPLING TECHNIQUES FOR GENERATING MELODIES WITH A TRANSFORMER LANGUAGE MODEL" by Mathias et al. explains like follows about three sampling methods, top K, nucleus(top P), typical sampling:

The most obvious method is ancestral sampling, where one token at a time is sampled based on the predicted distribution, conditioned on the previously generated tokens. However, it has been shown that truncating the conditional distribution (by setting the probability of specific tokens to zero, followed by renormalising), can lead to better sample quality than the non-truncated variant. An example of distribution truncation is top-k sampling, where all but the k most probable tokens are zeroed. In [12], the authors showed that top-k sampling generates more coherent samples than the nontruncated variant. In [6], it is explained that the quality improvement of top-k sampling is caused by removing unreliably estimated low-probability tokens, and it is found that top-k sampling mitigates the problem. However, it is also shown that top-k sampling is sensitive to the distribution’s entropy (see Section 3.3), making it hard to select a value of k that fits both high and low certainty conditions. As a solution, they propose nucleus sampling that assigns zero probability to the largest set of least probable tokens that together have a probability below a given threshold. The authors find that the samples produced using the technique are preferred by humans over other sampling techniques. Nucleus sampling has been used in music generation in [13–15], but its effects are difficult to quantify without comparisons to the non-truncated case. Although nucleus sampling mitigates the problem of poorly estimated low-probability tokens, it does not prevent generating degenerated repetitive sequences caused by low entropy distributions (see Section 3). As a solution, in [7], the authors propose typical sampling and show that this technique prevents degenerated sample generation.

Nucleus sampling

Paper: https://arxiv.org/abs/1904.09751

Code

def top_p_sampling(logits, thres=0.9):
  sorted_logits, sorted_indices = torch.sort(logits, descending=True)
  cum_probs = torch.cumsum(F.softmax(sorted_logits, dim=-1), dim=-1)

  sorted_indices_to_remove = cum_probs > thres
  sorted_indices_to_remove[..., 1:] = sorted_indices_to_remove[..., :-1].clone()
  sorted_indices_to_remove[..., 0] = 0

  # Create an empty tensor to hold the new logits
  new_logits = logits.clone()

  # Use the sorted indices to place the '-inf' in the original places
  indices_to_remove = sorted_indices[sorted_indices_to_remove]
  new_logits[..., indices_to_remove] = float('-inf')
  return new_logits

Typical sampling

paper: https://arxiv.org/abs/2202.00666

Code

# refered: https://github.com/cimeister/typical-sampling
def typical_sampling(logits, thres=0.99):
  # calculate entropy
  normalized = torch.nn.functional.log_softmax(logits, dim=-1)
  p = torch.exp(normalized)
  ent = -(normalized * p).nansum(-1, keepdim=True)

  # shift and sort
  shifted_scores = torch.abs((-normalized) - ent)
  sorted_scores, sorted_indices = torch.sort(shifted_scores, descending=False)
  sorted_logits = logits.gather(-1, sorted_indices)
  cumulative_probs = sorted_logits.softmax(dim=-1).cumsum(dim=-1)

  # Remove tokens with cumulative mass above the threshold
  last_ind = (cumulative_probs < thres).sum(dim=-1)
  last_ind[last_ind < 0] = 0
  sorted_indices_to_remove = sorted_scores > sorted_scores.gather(-1, last_ind.view(-1, 1, 1))
  # if self.min_tokens_to_keep > 1:
  #     # Keep at least min_tokens_to_keep (set to min_tokens_to_keep-1 because we add the first one below)
  #     sorted_indices_to_remove[..., : self.min_tokens_to_keep] = 0
  indices_to_remove = sorted_indices_to_remove.scatter(2, sorted_indices, sorted_indices_to_remove)

  scores = logits.masked_fill(indices_to_remove, float("-inf"))
  return scores