[Symbolic-Music-Encoding]#6.0 Evaluation Algorithms

In this post, I will discuss the evaluation algorithms that enable us to compare REMI and NB encoding in the same manner. We suggest two distinct methods for this implementation:

• The method of guided conditional probability in NB;note-based
• The method of redistributing probability in REMI

Guided conditional probability

about NB encoding

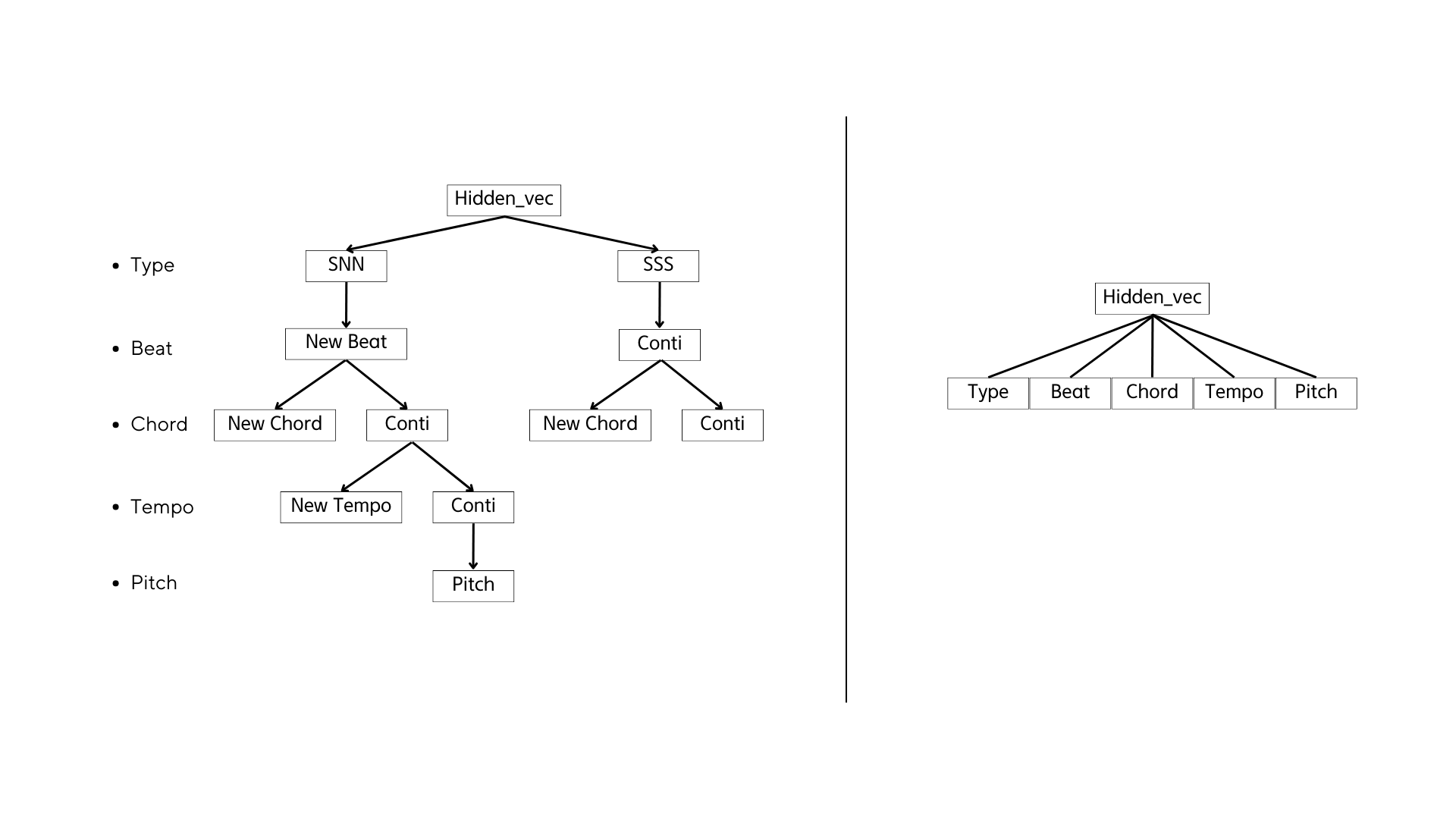
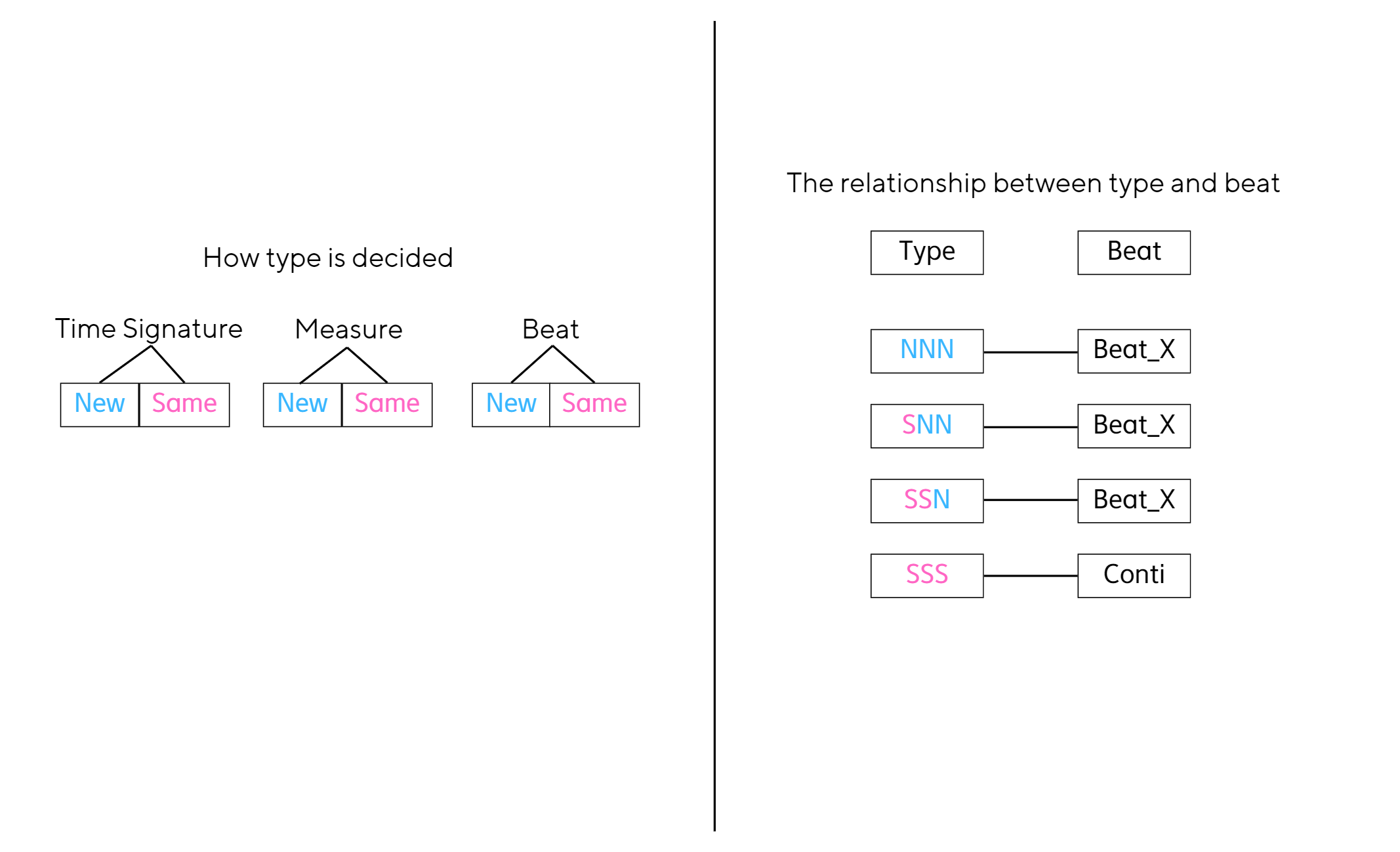
type features

In contrast to other encodings, the type features in our NB have multiple functions. They are:

• Signaling the start and end of a sequence (SOS/EOS)
• Predicting time signatures
• Anticipating changes in measures

vocab of type feature in SOD datasets

relationship between type and beat

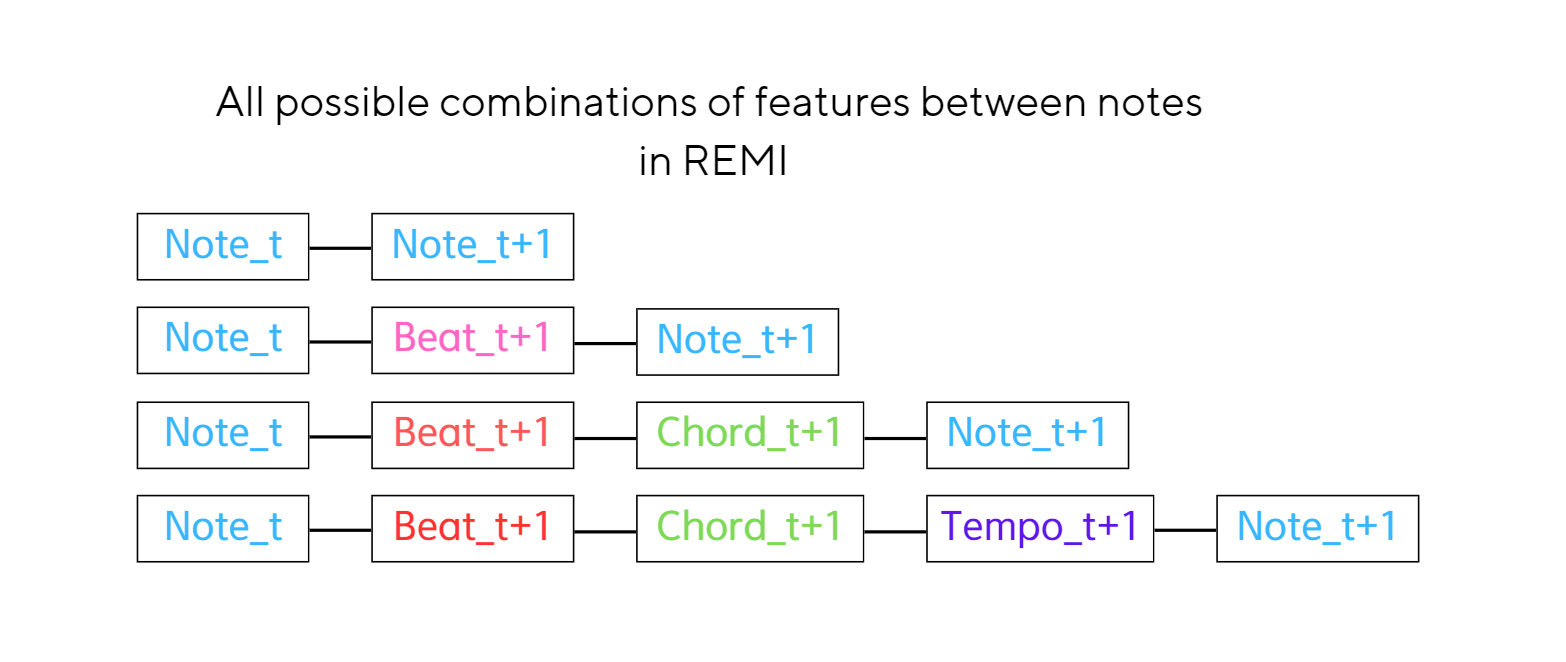
about REMI encoding

no Conti

In REMI, there are no Conti(continuous) tokens. As per the algorithm, if there's no change in a note's metrical information (beat, chord, tempo), the code simply omits adding that information.

Neglect kewords

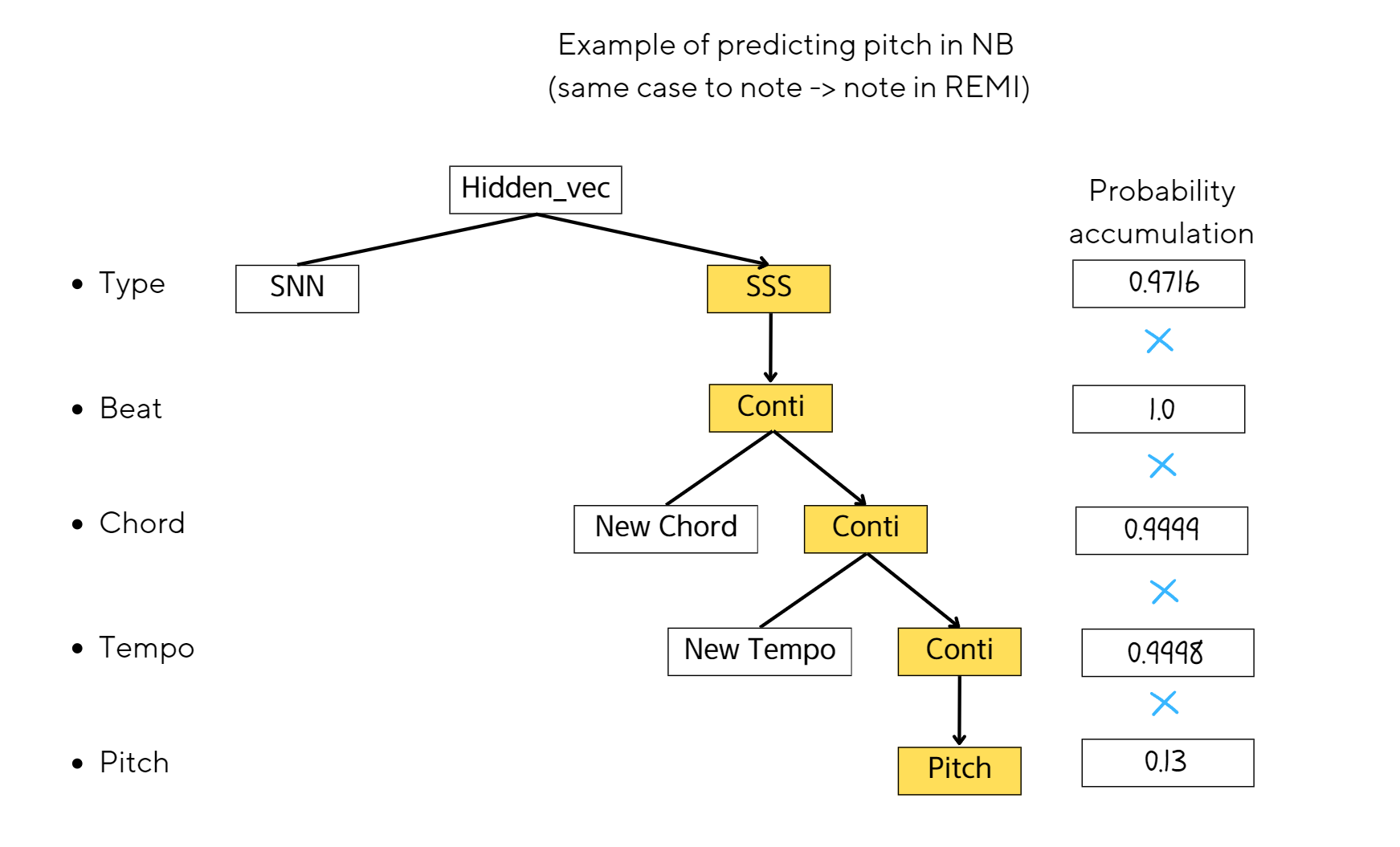
By deeming three keywords, "SSS", "SSN", and "Conti", as negligible (the probability of each kewords are neglected, but the probabilities are accumulated for the next features), we can compute the guided conditional probability in NB for an equitable comparison with REMI. Two scenarios require consideration:

• New beats
• New notes

New beats

When new beats are projected in NB from a given type, it's reasonable to presume that "SSN" has already anticipated the possibilities of new beats, thereby eliminating the probabilities of a continuous beat. Therefore, we can equate new "beat" in REMI to "P(beat_x | SSN)" in NB.

New notes

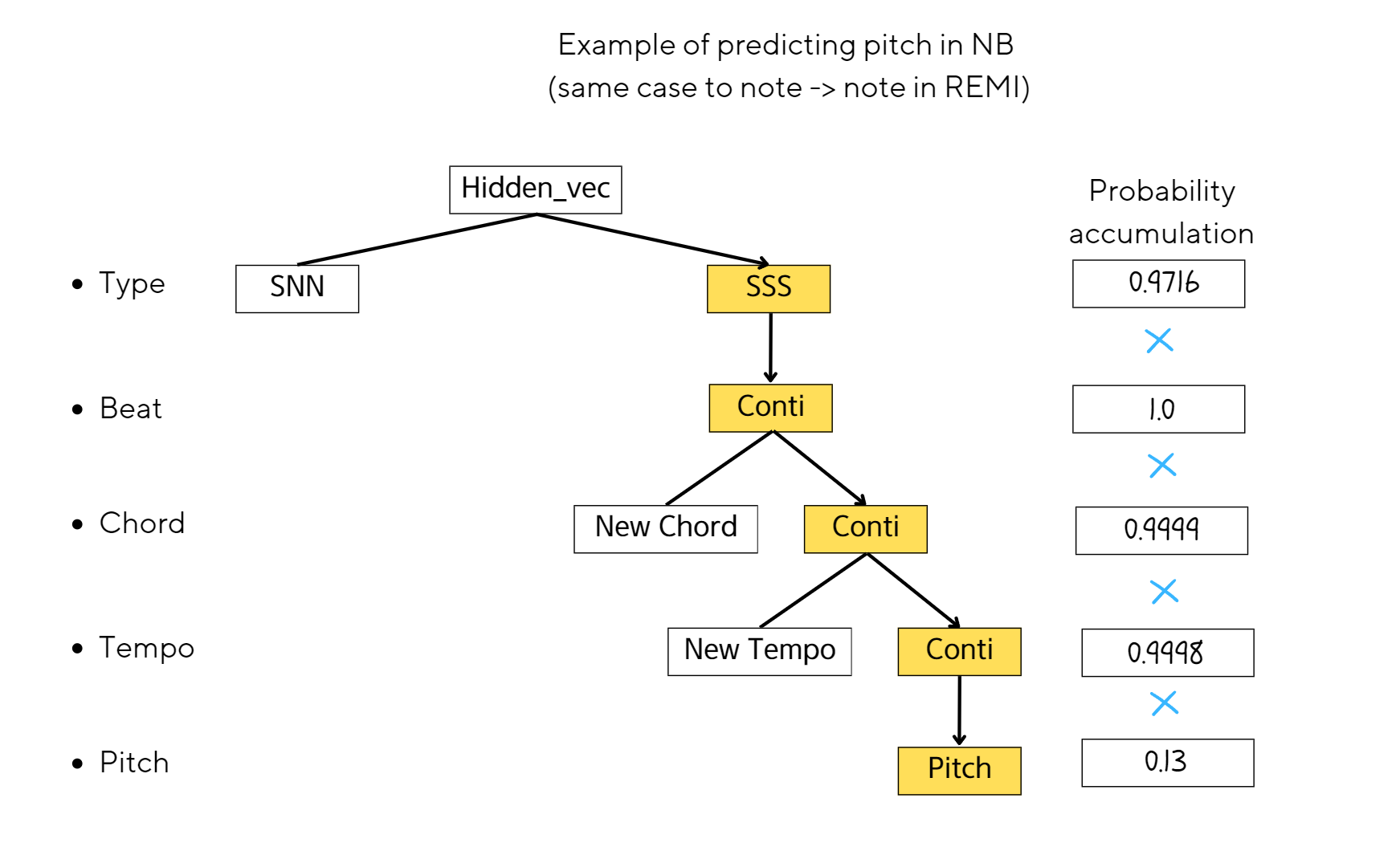
When new notes are projected in NB from a given beat, then we can equate new "note" in REMI to "P(pitch | SSS, Conti)" in case no chord and tempo features are considered.

mathematical expressions of probability of pitch

$p(x_{(t, pitch)}=y|x_1,\dots,x_{t-1}) = p(x_{(t, beat)}=y_{beat}|x_1,\dots,x_{t-1}) \times p(x_{(t, pitch)}=y_{pitch}|x_1,\dots,x_{t-1},x_{(t, beat)})$

Example of predicting pitch in NB

Shortcomings

Nonetheless, I'm not sure whether REMI truly predicts new pitch following the fixed sequence as NB. Despite the order of features in the sequence always being the same in REMI, it remains uncertain whether these order-bound multiplications are also valid in REMI.

Redistributing probability