Setup
Google Colaboratory를 활용해서 set up 절차를 간소화하여 실습을 진행해볼 수 있었다.
https://cs231n.github.io/assignments2020/assignment1/
링크에 assignment 1의 파일을 다운로드하고 동영상 튜토리얼을 따라가면 된다.(구글 계정과 연동에서 권한을 모두 부여해야 정상적으로 mount가 된다.)
과제는 knn.ipynb와 k_nearest_neighbor.py를 수정하는 방식으로 이루어진다.
문제해결
과제는 knn.ipynb와 k_nearest_neighbor.py를 수정하는 방식으로 이루어진다.
two loop distance
첫번째 문제는 distances를 two loop를 사용해서 구하는 코드를 만드는 것이다.
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0] # 500
num_train = self.X_train.shape[0] # 5000
dists = np.zeros((num_test, num_train))
for i in range(num_test):
for j in range(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension, nor use np.linalg.norm(). #
#####################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# 500 * 3072와 5000 * 3072의 행렬을 연산해야 한다.
# loop에서 i, j 각각의 행들을 뽑아 낼수 있기 때문에 그대로 계산을 해주면 된다.
# 각 행들의 요소들은 각자 빼지고, 제곱이 된 다음 행들의 모든 요소들은 더해진뒤에
# 제곱근으로 하나의 값이 된다.
# 이 모든 값들은 500, 5000의 dists 행렬에 저장이 된다.
dists[i][j] = np.sqrt(np.sum(np.square(X[i]-self.X_train[j])))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distsInline Question 1
# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
plt.imshow(dists, interpolation='none')
plt.show()
Notice the structured patterns in the distance matrix,
where some rows or columns are visible brighter.
(Note that with the default color scheme black indicates
low distances while white indicates high distances.)What in the data is the cause behind the distinctly bright rows?
What causes the columns?
YourAnswer: a test image matches to none of the train image makes the bright row,
the opposite way makes the bright columnInline Question 2
YourAnswer: 1, 3
YourExplanation:
1.about specific image, μ can be considered as a constant number.
its substraction can't affect the higher or lower value of L1 distance
2.mean(i,j) differs on every pixels. thus its substraction affects
3.σ as a number of specific image, it doesn't change relative distance L1
4.same as 2, mean(i,j) already affects the consquences
5.only L2 distance isn't affectedone loop distance
이번에는 one loop를 이용해서 거리의 차를 구한다.
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0] # 500
num_train = self.X_train.shape[0] # 5000
dists = np.zeros((num_test, num_train))
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
# Do not use np.linalg.norm(). #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# X_train은 5000 * 3072의 행렬이다. broadcasting을 이용하면
# 각각의 행에 연산을 쉽게 적용할 수 있다.
dists[i] = np.sqrt(np.sum(np.square(self.X_train-X[i]),axis=1))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distsno loop distance
루프를 사용하지 않고 거리의 차를 구한다.
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy, #
# nor use np.linalg.norm(). #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# l2 distance는 두 행렬의 행의 각 요소들의 차를 제곱 후 더해서 제곱근으로 만들 수도 있지만
# 행을 통한 요소들의 계산을 행렬의 차원에서 계산을 해볼 수 있다.
# 즉, 각 요소들의 거리의 차는 행렬의 연산으로도 구할 수가 있다는 것이다.
# X_train의 연산 결과는 1 * 5000
# X의 연산 결과는 500 * 1이 된다.
# 다만 결과값이 500 * 5000의 행렬이 되야하므로 이 결과값에 맞추어 행렬의 식을 짰다는 것
# 이상으로 이해가 되지는 않는다.
# 왜냐하면 각 요소들의 연산이 (a-b)^2이 되는 것은 알겠는데
# 이게 행렬이 -2AB + A^2 + B^2이 되는 것과 무슨 관련이 있단 말일까?
# (추가) 다시 생각해보니 -2AB와 -2BA의 차이는 500 * 5000과 5000 * 500의
# 행렬 생김새의 차이를 만들 뿐이었다. 연산된 요소들은 대칭의 형태로 같다는 것을 확인했다.
dists = np.sqrt(-2*np.dot(X, self.X_train.T) + np.sum(np.square(self.X_train), axis=1) + np.transpose([np.sum(np.square(X), axis=1)]))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distscross-validation
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for k in k_choices:
k_to_accuracies[k] = []
for i in range(num_folds):
X_train_fold = np.concatenate([x for num, x in enumerate(X_train_folds) if num!=i])
y_train_fold = np.concatenate([y for num, y in enumerate(y_train_folds) if num!=i])
classifier.train(X_train_fold, y_train_fold)
y_fold_pred = classifier.predict(X_train_folds[i], k=k, num_loops=0)
num_correct = np.sum(y_fold_pred == y_train_folds[i])
accuracy = float(num_correct) / X_train_folds[i].shape[0]
k_to_accuracies[k].append(accuracy)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))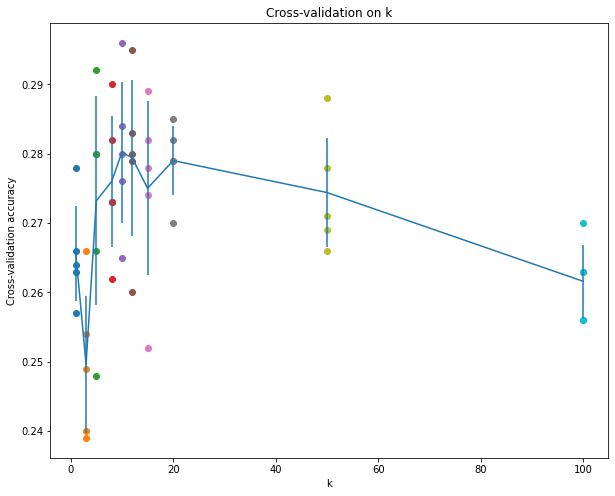
Inline Question3
Which of the following statements about k -Nearest Neighbor ( k -NN) are true in a classification setting, and for all k ? Select all that apply.
1.The decision boundary of the k-NN classifier is linear.
2.The training error of a 1-NN will always be lower than or equal to that of 5-NN.
3.The test error of a 1-NN will always be lower than that of a 5-NN.
4.The time needed to classify a test example with the k-NN classifier grows with the size of the training set.
5.None of the above.YourAnswer: 2, 4
YourExplanation:
1.Decision boundary is calcuated by the distance
2.because it usually overfit to wrong class
3.wrong, see the procedure
4.sure, it campares every traing set to a test imagereference
https://yun905.tistory.com/2
https://rchoi-19-4-2.tistory.com/129
