https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95%EB%8C%80%EC%88%98%ED%95%99
에서 내용을 정리함
선형대수학이란?
선형대수학은 선형 함수(or 사상, 연산, 변환)에 대한 대수학으로서 벡터 공간, 벡터, 선형 변환, 행렬, 연립 선형 방정식 등을 연구하는 대수학의 한 분야이다. 현대 선형대수학은 그중에서도 벡터 공간이 주 연구 대상이다
선형성
"선형"이라는 성질은 행렬과 동전의 양면과 같은 관계를 가지고 있다. 어떤 연산이 선형이라면 그것은 행렬로 표현이 가능하며, 어떤 행렬은 반대로 어떤 선형연산으로 해석될 수 있다. 선형과 대립되는 개념으로 비선형이 있는데, x^n, sinx, cosx 등 일차함수와 같은 형태의 성질을 만족시키지 않는 함수들을 가리킨다.
(정의) 정의역 X에서 임의의 원소 u,v를 치역 Y에 대응시키는 연산 T는 다음과 같은 성질을 만족시킬 때 "선형"이라고 한다. 여기서 c는 임의의 상수이다.
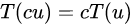
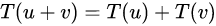
선형대수학의 기초
http://blog.daum.net/eigenvalue/10856412 이 사이트에서 pdf를 공부하면 도움이 된다.
선형대수학의 주요 내용들
-
벡터와 행렬
-
가우스-요르단 소거법 : 가우스-요르단 소거법은 행렬의 행 간의 연산이다. 이 연산은 행렬로 구성된 방정식의 해를 구하는 방법을 제시한다. 또한 이 계산과정을 뒷받침하는 이론에 대해서도 공부하며, 소거법의 결과로 구해진 해를 해석하는 방법도 공부한다. 가우스-요르단 소거법은 방정식의 해를 보존할 수 있는 연산들로 이루어져 있으며, 세 가지가 존재한다.
- 행렬의 행을 그 행의 상수배만큼으로 대체하여도 그 행렬 방정식의 해는 보존된다.
- 행렬의 한 행의 상수배를 다른 행에 더하더라도 그 행렬 방정식의 해는 보존된다.
- 행렬의 한 행과 다른 행을 교환하더라도 그 행렬 방정식의 해는 보존된다.
-
행렬 연산자와 특정 형태의 행렬 : 행렬에 관계된 연산자들과 특정한 형태의 행렬에 대해 배운다. 전치, 트레이스, 역행렬등이 중요한 행렬연산자이다. 특정한 형태의 행렬로는 단위행렬, 상부삼각행렬, 하부삼각행렬, 대칭행렬 등에 대해 배운다. 상부삼각행렬과 하부삼각행렬을 이용해 행렬을 표현하는 LU분해법도 배운다.
-
선형독립 : 벡터들의 일차독립
-
행렬식(판별식) : 행렬식의 정의와 행렬식을 구하는 방법을 공부한다. 또한 대수적으로 행렬식을 표현하고 행렬식에 관계된 정리들을 배운다.
-
고윳값과 고유벡터: 행렬의 고윳값과 고유벡터에 대해 공부한다. 행렬식을 통해 고윳값을 찾고, 고윳값과 가우스 소거법을 통해 고유벡터를 찾는 과정을 익힌다. 그 외에도 고윳값과 고유벡터에 관계된 정리들에 대해 공부한다.
-
선형연산자: 이 부분에서는 선형연산과 행렬 간의 상호성에 대해 주의 깊게 다룬다.
-
벡터 공간: 벡터 공간을 행렬을 통해 해석하는 방법을 익힌다. 선형연산과 행렬 간의 상호성과 마찬가지로 벡터 공간과 행렬 사이에는 깊은 상호성이 있다. 중요한 개념들로는 다음과 같은 것들이 있다.
-
기저, 차원: 기저란, 어떤 벡터 공간을 이루는 벡터들을 말한다. 이 벡터들은 일차독립이여야 하며, 이 벡터들의 선형조합으로 그 벡터 공간의 모든 벡터를 표현할 수 있어야 한다. 직관적인 예를 들면 x축, y축, z축은 3차원공간의 기저이다. 차원이란 기저를 구성하는 벡터들의 숫자를 말한다.
-
기본공간, 차원 정리, 계수정리, 피봇정리: 기본공간은 행렬과 벡터 공간 사이의 다리와 같은 역할을 한다. 기본공간에는 영공간, 행공간, 열공간 등이 있다. 차원정리, 계수정리, 피봇정리는 이 기본공간들의 차원과 기저에 대해 유용한 알고리즘을 제공한다.
-
벡터의 직교화: 직교화된 벡터들에 대해 공부한다. 직교화된 벡터들이란 다른 벡터와의 내적값이 0인 벡터들을 의미한다.
-
그람-슈미트 직교정규화: 그람-슈미트 직교정규화를 통해 주어진 벡터의 집합을 직교화된 벡터의 집합으로 변환하는 법을 다룬다. 벡터의 직교화에서 배운 개념을 바탕으로 전개해 나간다.
-
상사성과 대각화: 상사성이란 두 행렬이 동일한 연산을 의미한다는 뜻이다. 즉, 두 행렬이 서로 다른 두 벡터 공간에서 동일한 연산을 처리하고 있다는 의미이다. 그러므로 상사성을 가진 두 행렬은 적당한 기저를 선택해서 서로를 표현할 수 있다. 대각화란 이 상사성을 계산 측면에서 응용한 것으로 특정 행렬을 대각행렬로 표현하는 과정이다.
선형성(Linearity) 정의 및 1차연립방정식의 의미
https://techblog-history-younghunjo1.tistory.com/65 참고
row form 형태의 행렬과 벡터의 형태로 1차 연립방정식을 해결하는 것의 차이를 인지하자.
