[파이토치로 배우는 자연어 처리] #2 신경망의 기본 구성 요소

Clay Ryu's sound lab·2022년 3월 23일

Note for 2022

목록 보기

23/47

2-1.퍼셉트론 : 가장 간단한 신경망

import torch
import torch.nn as nn

class Perceptron(nn.Module):
  def __init__(self, input_dim):
    super(Perceptron, self).__init__()
    self.fc1 = nn.Linear(input_dim, 1)

  def forward(self, x_in):
  	# squeeze함수는 차원이 1인 차원을 제거해준다.
    return torch.sigmoid(self.fc1(x_in)).squeeze()

2-2.활성화 함수

시그모이드

1 / 1 + e^-x
시그모이드 함수는 입력 범위 대부분에서 매우 빠르게 포화된다.(극단적인 출력을 만든다.) 이로 인해 gradient가 0이 되거나 발산해서 부동소수 오버플로가 되는 문제가 발생한다. 이 때문에 시그모이드 함수는 binary classification에서 출력층에만 사용이 된다.

import matplotlib.pyplot as plt

x = torch.range(-5., 5., 0.1)
y = torch.sigmoid(x)
plt.plot(x.numpy(), y.numpy())
plt.show()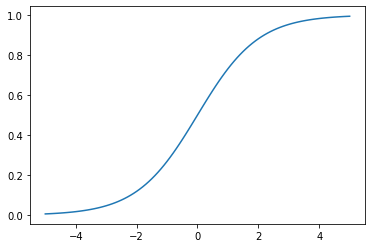

하이퍼볼릭 탄젠트

x = torch.range(-5., 5., 0.1)
y = torch.tanh(x)
plt.plot(x.numpy(), y.numpy())
plt.show()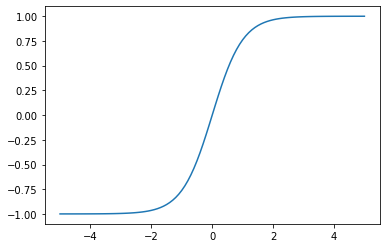

ReLU rectified linear unit

f(x) = max(0, x)

relu = torch.nn.ReLU()
x = torch.range(-5., 5., 0.1)
y = relu(x)

plt.plot(x.numpy(), y.numpy())
plt.show()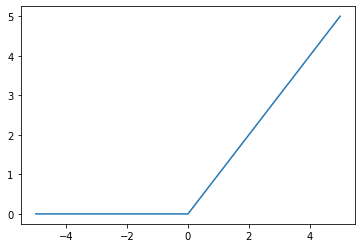

PReLU parametric ReLU

f(x) = max(x, ax)

Softmax

softmax = torch.nn.Softmax(dim=1)
x_input = torch.randn(1,3)
y_output = softmax(x_input)
print(x_input)
print(y_output)
print(torch.sum(y_output, dim=1))

2-3.손실함수

MSE mean squared error

mse_loss = torch.nn.MSELoss()
# requires_grad = Ture 로 설정하면 이제 이 텐서에 대한 기울기를 저장하게 된다.
outputs = torch.randn(3,5, requires_grad=True)
targets = torch.randn(3,5)
loss = mse_loss(outputs, targets)
print(loss)

Categorical Cross-entropy

target이 one-hot encoding이 된 라벨이든 sparse한 라벨이든 상관없이 loss값이 정상 출력이 된다.

ce_loss = torch.nn.CrossEntropyLoss()
outputs = torch.randn(3,5, requires_grad=True)
targets = torch.randn(3,5)
# targets = torch.tensor([1, 0, 4], dtype=torch.int64)
loss = ce_loss(outputs, targets)
print(loss)

Binary Cross-entropy

bce_loss = torch.nn.BCELoss()
sigmoid = nn.Sigmoid()
probabilities = sigmoid(torch.randn(4,1, requires_grad=True))
# view와 reshape의 차이는 정리해둠
targets = torch.tensor([1,0,1,0], dtype=torch.float32).view(4,1)
loss = bce_loss(probabilities, targets)
print(probabilities)
print(loss)

2-4.지도 학습 훈련

모델을 선택하고 손실함수를 선택하고, 옵티마이저를 선택하고, 미니배치를 통해서 학습을 한다. 이번 내용은 그간 밑바닥 딥러닝에서 공부한 내용들이므로 간단히 훑어보고 넘어간다.

2-5.부가적인 훈련 개념

평가지표evaluation metric
데이터의 분할, k fold cross validation
조기종료early stopping
하이퍼 파라미터 : 손실 함수, 옵티마이저, 학습률, 층의 크기, 에포크의 수
규제 : 수치 최적화 이론에서 유래, 파이토치에서는 옵티마이저의 weight_decay값으로 조절, L2 Regularization의 lambda값