선형대수의 필요
Deep learning을 이해하기 위해서 반드시 선형대수 + 행렬미분 + 확률의 탄탄한 기초가 필요하다.
핵심 아이디어가 행렬에 관한 식으로 표현되는 경우가 많다.
기본 표기법
벡터 x는 기본적으로 열벡터로 생각한다.
행벡터를 표기하기 위해서는 x^T로 적어준다.
import numpy as np
x = np.array([10.5, 5.2, 3.25])
#행벡터로 보이지만 shape을 보면 열벡터이다.
x.shape -> (3,)
A = np.array([
[10,20,30],
[40,50,60]
])
A ->
array([[10, 20, 30],
[40, 50, 60]])
A.shape -> (2, 3)
j = 1
A[:, j] -> array([20, 50])행렬의 곱셈Matrix Multiplication
벡터 X 벡터 Vector-Vector Products
내적inner product, dot product
import numpy as np
x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
x.dot(y) -> 32
y.dot(x) -> 32외적outer product
x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
x = np.expand_dims(x, axis=1)
y = np.expand_dims(y, axis=0)
x.shape, y.shape -> ((3, 1), (1, 3))
np.matmul(x,y) ->
array([[ 4, 5, 6],
[ 8, 10, 12],
[12, 15, 18]])외적으로 표현하기
행렬 X 벡터 Matrix-Vector Products
행의 행렬과 열벡터의 곱
열의 행렬과 열벡터의 곱
행벡터와 열의 행렬의 곱
행벡터와 행의 행렬의 곱
#2x3 matrix
A = np.array([
[1,2,3],
[4,5,6]
])
#3x1 vector
ones = np.ones([3,1])
np.matmul(A, ones) ->
#2x1 vector
array([[ 6.],
[15.]])행렬 X 행렬 Matrix-Matrix Products
하나의 행렬을 열로 표현 했을 때의 곱
하나의 행렬을 행으로 표현 했을 때의 곱
중요 연산과 성질들 Operations and Properties
정방행렬(square matrix): 행과 열의 개수가 동일
상삼각행렬(upper triangular matrix): 정방행렬이며 주대각선 아래 원소들이 모두 0
하삼각행렬(lower triangular matrix): 정방행렬이며 주대각선 위 원소들이 모두 0
대각행렬(diagonal matrix): 정방행렬이며 주대각선 제외 모든 원소가 0
np.diag([4, 5, 6])단위행렬(identity matrix): 대각행렬이며 주대각선 원소들이 모두 1. 𝐼 로 표시한다.
np.eye(3)전치 Transpose
행렬을 전치하는 것은 그 행렬을 뒤집는 것으로 생각할 수 있다. 행렬 𝐴∈ℝ𝑚×𝑛 이 주어졌을 때 그것의 전치행렬은 𝐴^𝑇∈ℝ𝑛×𝑚 으로 표시하고 각 원소는 다음과 같이 주어진다.
성질은 다음과 같다.
역전치 : (𝐴𝑇)^𝑇=𝐴
곱분배 : (𝐴𝐵)^𝑇=𝐵𝑇𝐴𝑇
합분배 : (𝐴+𝐵)^𝑇=𝐴𝑇+𝐵𝑇
A = np.array([
[1,2,3],
[4,5,6]
])
A.T ->
array([[1, 4],
[2, 5],
[3, 6]])대칭행렬 Symmetic Matrices
정방행렬 𝐴 가 𝐴𝑇 와 동일할 때 대칭행렬이라고 부른다. 𝐴=−𝐴𝑇 일 때는 반대칭(anti-symmetric)행렬이라고 부른다.
𝐴𝐴^𝑇 는 항상 대칭행렬이다.
𝐴+𝐴^𝑇 는 대칭, 𝐴−𝐴^𝑇 는 반대칭이다.
대각합 Trace
정방행렬 𝐴∈ℝ𝑛×𝑛 의 대각합은 tr(𝐴)로 표시하고 그 값은 ∑𝐴𝑖𝑖 이다.
대각합은 다음과 같은 성질을 가진다.
전치: For 𝐴∈ℝ𝑛×𝑛 , tr𝐴=tr𝐴^𝑇
합분배 : For 𝐴,𝐵∈ℝ𝑛×𝑛 , tr(𝐴+𝐵)=tr𝐴+tr𝐵
상수곱대각합 : For 𝐴∈ℝ𝑛×𝑛,𝑡∈ℝ , tr(𝑡𝐴)=𝑡tr𝐴
정방행렬대각합 : For 𝐴,𝐵 such that 𝐴𝐵 is square, tr𝐴𝐵=tr𝐵𝐴
For 𝐴,𝐵,𝐶 such that 𝐴𝐵𝐶 is square, tr𝐴𝐵𝐶=tr𝐵𝐶𝐴=tr𝐶𝐴𝐵 , and so on for the product of more matrices
A = np.array([
[100, 200, 300],
[ 10, 20, 30],
[ 1, 2, 3],
])
np.trace(A) -> 123Norms
L2 norm은 유클리드 거리이다.
import numpy.linalg as LA
LA.norm(np.array([3, 4])) -> 5.0Frobenius norm(행렬에 대해서)
L2 norm의 square 값은 단순하게 그 벡터를 전치한 벡터와 내적하면 된다. 이를 행렬에 적용한다면 행렬 곱의 trace 값을 쓰면 된다.
A = np.array([
[100, 200, 300],
[ 10, 20, 30],
[ 1, 2, 3],
])
LA.norm(A) -> 376.0505285197722
np.trace(A.T.dot(A))**0.5 -> 376.0505285197722선형독립Linear Independence과 Rank
벡터들의 집합 {𝑥1,𝑥2,…,𝑥𝑛}⊂ℝ𝑚 에 속해 있는 어떤 벡터도 나머지 벡터들의 선형조합으로 나타낼 수 없을 때 이 집합을 선형독립(linear independent)이라고 부른다. 역으로 어떠한 벡터가 나머지 벡터들의 선형조합으로 나타내질 수 있을 때 이 집합을 (선형)종속(dependent)이라고 부른다.
Rank
Column rank: 행렬 𝐴∈ℝ𝑚×𝑛 의 열들의 부분집합 중에서 가장 큰 선형독립인 집합의 크기
Row rank: 행렬 𝐴∈ℝ𝑚×𝑛 의 행들의 부분집합 중에서 가장 큰 선형독립인 집합의 크기
모든 행렬의 column rank와 row rank는 동일하다. 따라서 단순히 rank(𝐴) 로 표시한다.
다음의 성질들이 성립한다.
랭크의 크기 : For 𝐴∈ℝ𝑚×𝑛, rank(𝐴)≤min(𝑚,𝑛)
풀랭크 : If rank(𝐴)=min(𝑚,𝑛), then 𝐴 is said to be full rank
전치랭크 : For 𝐴∈ℝ𝑚×𝑛, rank(𝐴)=rank(𝐴^𝑇)
합랭크 : For 𝐴∈ℝ𝑚×𝑛, 𝐵∈ℝ𝑛×𝑝, rank(𝐴+𝐵)≤min(rank(𝐴),rank(𝐵))
합랭크 : For 𝐴,𝐵∈ℝ𝑚×𝑛, rank(𝐴+𝐵)≤rank(𝐴)+rank(𝐵)
A = np.array([
[1, 4, 2],
[2, 1, -3],
[3, 5, -1],
])
# 3번째 벡터가 종속적이다.
LA.matrix_rank(A) -> 2역행렬 The Inverse
정방행렬 𝐴∈ℝ𝑛×𝑛 의 역행렬 𝐴−1 은 다음을 만족하는 정방행렬( ∈ℝ𝑛×𝑛 )이다.
𝐴^−1𝐴 = 𝐼 = 𝐴𝐴^−1
𝐴의 역행렬이 존재할 때, 𝐴를 invertible 또는 non-singular하다고 말한다.
𝐴 의 역행렬이 존재하기 위해선 𝐴는 full rank여야 한다.
역역행렬 : (𝐴−1)^−1 = 𝐴
분배 : (𝐴𝐵)^−1 = 𝐵−1𝐴−1
전치와역행렬 : (𝐴^−1)𝑇=(𝐴^𝑇)−1
A = np.array([
[1, 2],
[3, 4],
])
LA.inv(A) ->
array([[-2. , 1. ],
[ 1.5, -0.5]])직교 행렬 Orthogonal Matrices
𝑥^𝑇𝑦=0가 성립하는 두 벡터 𝑥,𝑦∈ℝ𝑛를 직교orthogonal라고 부른다. ‖𝑥‖ = 1인 벡터 𝑥∈ℝ𝑛를 정규화normalized된 벡터라고 부른다.
모든 열들이 서로 직교이고 정규화된 정방행렬 𝑈∈ℝ𝑛×𝑛를 직교행렬이라고 부른다.
따라서 다음이 성립한다.
행렬의 직교 : 𝑈^𝑇𝑈=𝐼
행렬의 직교 : 𝑈𝑈𝑇=𝐼 이건 밑에서 증명
역행렬과 전치행렬 : 𝑈^−1=𝑈^𝑇
L2norm : ‖𝑈𝑥‖2=‖𝑥‖2 for any 𝑥∈ℝ𝑛
치역Range, 영공간Nullspace
벡터의 집합( {𝑥1,𝑥2,…,𝑥𝑛} )에 대한 생성(span)
x벡터들의 선형조합
행렬의 치역range
행렬 𝐴∈ℝ𝑚×𝑛의 치역 R(A)는 A의 모든 열들에 대한 생성(span)이다.(열공간이라는 뜻인데 왜 C가 아니고 R로 표시하는지는 모르겠다.)
영공간nullspace
행렬 𝐴∈ℝ𝑚×𝑛의 영공간(nullspace) N(A)는 𝐴와 곱해졌을 때 0이 되는 모든 벡터들의 집합이다.
중요한 성질
이부분이 쉽게 이해가 안간다면 영공간은 행공간의 직교 여공간이라는 것만을 알아두어도 좋을듯 하다. Row(A)⊥= Nul(A)
https://soohee410.github.io/orthogonality 참고
투영projection
행렬식Determinant
A = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 0]
])
LA.det(A) -> 27.0행렬식의 기하학적 해석
행 벡터들의 선형조합(단 조합에 쓰이는 계수들은 0에서 1사이)이 나타내는 ℝ𝑛 공간 상의 모든 점들의 집합 𝑆 를 생각해보자. 중요한 사실은 행렬식의 절대값이 이 𝑆 의 부피(volume)과 일치한다는 것이다!
행렬식의 중요한 성질들
I의 행렬식 : |𝐼|=1
상수곱의 행렬식 : 𝐴 의 하나의 행에 𝑡∈ℝ 를 곱하면 행렬식은 𝑡|𝐴|
1행과2행을 교환한 행렬식 : 𝐴 의 두 행들을 교환하면 행렬식은 −|𝐴|
전치행렬의 행렬식 : For 𝐴∈ℝ𝑛×𝑛, |𝐴|=|𝐴^𝑇|
곱분해 행렬식 : For 𝐴,𝐵∈ℝ𝑛×𝑛, |𝐴𝐵|=|𝐴||𝐵|
행렬식이 0이면 : For 𝐴∈ℝ𝑛×𝑛, |𝐴|=0, if and only if A is singular(non-invertible). 𝐴가 singular이면 행들이 linearly dependent할 것인데, 이 경우 𝑆의 형태는 부피가 0인 납작한 판의 형태가 될 것이다.
역행렬의 행렬식 : For 𝐴∈ℝ𝑛×𝑛 and 𝐴 non-singular, |𝐴^−1|=1/|𝐴|
이차형식 Quadratic Forms
정방행렬 𝐴∈ℝ𝑛×𝑛 와 벡터 𝑥∈ℝ𝑛 가 주어졌을 때, scalar값 𝑥^𝑇𝐴𝑥 를 이차형식(quadratic form)이라고 부른다. 다음과 같이 표현할 수 있다.
scalar의 transpose는 같으므로 다음이 성립한다.
따라서 이차형식에 나타나는 행렬을 대칭행렬로 가정하는 경우가 많다.
Positive definite 그리고 negative definite 행렬은 full rank이며 따라서 invertible이다.
Gram matrix
임의의 행렬 𝐴∈ℝ𝑚×𝑛이 주어졌을 때 행렬 𝐺=𝐴^𝑇𝐴를 Gram matrix라고 부르고 항상 positive semi-definite이다. 만약 𝑚≥𝑛이고 𝐴가 full rank이면, 𝐺는 positive definite이다.
고유값Eigenvalues, 고유벡터Eigenvectors
A =
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 0]])
eigenvalues, eigenvectors = LA.eig(A)
eigenvalues, eigenvectors ->
(array([12.12289378, -0.38838384, -5.73450994]),
array([[-0.29982463, -0.74706733, -0.27625411],
[-0.70747178, 0.65820192, -0.38842554],
[-0.63999131, -0.09306254, 0.87909571]]))
#고유벡터는 열로 나온다.
eigenvectors[:, 0] ->
array([-0.29982463, -0.70747178, -0.63999131])
np.matmul(A, eigenvectors[:, 0]) ->
eigenvalues[0] * eigenvectors[:, 0] ->
array([-3.63474211, -8.57660525, -7.75854663])고유값, 고유벡터의 성질들
A의 trace는 고유값의 합과동일
A의 determinant는 고유값의 곱과동일
rank(𝐴) 는 0이 아닌 𝐴의 고유값의 개수와 같다.
𝐴 가 non-singular(역행렬이 존재)일 때, 1/𝜆𝑖 는 𝐴−1 의 고유값이다(고유벡터 𝑥𝑖 와 연관된). 즉, 𝐴−1𝑥𝑖=(1/𝜆𝑖)𝑥𝑖 이다.
대각행렬 𝐷=diag(𝑑1,…,𝑑𝑛) 의 고유값들은 𝑑1,…,𝑑𝑛 이다.
모든 고유값과 고유벡터들을 다음과 같이 하나의 식으로 나타낼 수 있다.
고유값, 고유벡터와 대칭행렬
대칭행렬 𝐴∈𝕊𝑛 가 가지는 놀라운 성질들
𝐴의 모든 고유값들은 실수값(real)이다.
𝐴의 고유벡터들은 orthonomal(orthogonal, normalized)이다.
따라서 임의의 대칭행렬 𝐴를 𝐴=𝑈Λ𝑈^𝑇 (𝑈는 위의 𝑋처럼 𝐴의 고유벡터들로 이뤄진 행렬)로 나타낼 수 있다.
𝐴∈𝕊𝑛=𝑈Λ𝑈^𝑇 라고 하자. 그러면
𝑦i^2가 양수이므로 위 식의 부호는 𝜆𝑖 값들에 의해서 결정된다. 만약 모든 𝜆𝑖>0 이면, 𝐴는 positive definite이고 모든 𝜆𝑖≥0 이면, 𝐴는 positive seimi-definite이다.
행렬미분 Matrix Calculus
The Gradient
행렬 𝐴∈ℝ𝑚×𝑛를 입력으로 받아서 실수값을 돌려주는 함수 𝑓:ℝ𝑚×𝑛→ℝ이 있다고 하자. 𝑓의 gradient는 다음과 같이 정의된다. gradient는 행렬이되고 그 원소는 편미분한 값이 된다.
특별히 𝐴가 벡터 𝑥∈ℝ𝑛 인 경우는,
The Hessian
2번 미분한다.
중요한 공식들
𝑥,𝑏∈ℝ𝑛 , 𝐴∈𝕊𝑛 일 때 다음이 성립한다.
최소제곱법Least Squares에 적용
행렬 𝐴∈ℝ𝑚×𝑛 (𝐴는 full rank로 가정)와 벡터 𝑏∈ℝ𝑛 가 주어졌고 𝑏가 행렬 A의 공간에 있지 않은 경우, 𝐴𝑥=𝑏를 만족하는 벡터 𝑥∈ℝ𝑛을 찾을 수 없다. 대신 𝐴𝑥가 𝑏와 최대한 가까워지는 𝑥, 즉 ‖𝐴𝑥−𝑏‖2의 제곱을 최소화시키는 𝑥를 찾는 문제를 고려할 수 있다. ‖𝑥‖2의 제곱은 𝑥^𝑇𝑥 이므로
마지막 식을 0으로 놓고 x의 근사값을 구하면
𝑥햇 = (𝐴^𝑇𝐴)^−1𝐴^𝑇𝑏가 된다.
미분을 사용하지 않은 증명은 아래 참조
https://soohee410.github.io/least_squares_sol
고유값과 최적화문제Eigenvalues as Optimization에 적용
다음 형태의 최적화문제를 행렬미분을 사용해 풀면 고유값이 최적해가 되는 것을 보일 수 있다. x의 l2 norm이 1일때 이차형식을 최대화하는 x를 구하기
제약조건이 있는 최소화문제는 Lagrangian을 사용해서 해결
다음을 만족해야 함
따라서 최적해 𝑥는 𝐴𝑥=𝜆𝑥를 만족해야 하므로 𝐴의 고유벡터만이 최적해가 될 수 있다. 고유벡터 𝑢𝑖는
을 만족하므로( 𝑦=𝑈^𝑇𝑢𝑖 ), 최적해는 가장 큰 고유값에 해당하는 고유벡터이다. U는 고유벡터 ui의 집합인 행렬
(아 포기마렵다...)
Autoencoder와 Principal Components Analysis (PCA)
아주 고차원의 데이터를 가지고 있을때 그것의 저장공간이 부족할때 가능하면, 주어진 정보를 많이 잃지 않으려면 이런 작업을 하게 된다.
Autoencoder의 응용예제
Dimensionality Reduction
Image Compression
Image Denoising
Feature Extraction : 데이터 전처리 단계에서 압축된 걸 사용하는게 도움이 될때가 있음
Image generation
Sequence to sequence prediction
Recommendation system
PCA
PCA를 가장 간단한 형태의 autoencoder로 생각할 수 있다. 이 관점으로 PCA를 유도할텐데, 이제까지 우리가 배운 것만으로 가능하다!
𝑚개의 점들 {𝑥1,…,𝑥𝑚}, 𝑥𝑖∈ℝ𝑛 이 주어졌다고 하자. 각각의 점들을 𝑙 차원의 공간으로 투영시키는 함수 𝑓(𝑥) = 𝑐∈ℝ𝑙 와 이것을 다시 𝑛 차원의 공간으로 회복하는 함수 𝑔(𝑐) 를 생각해보자. 𝑓를 인코딩 함수, 𝑔를 디코딩 함수라고 부르며 x 가 g(f(x))와 최대한 유사하기를 원한다.
디코딩 함수
함수 𝑔 는 간단한 선형함수로 정의하기로 한다.
𝑔(𝑐)=𝐷𝑐, 𝐷∈ℝ𝑛×𝑙
여기서 𝐷 는 열들이 정규화되어 있고 서로 직교하는 경우로 한정한다.
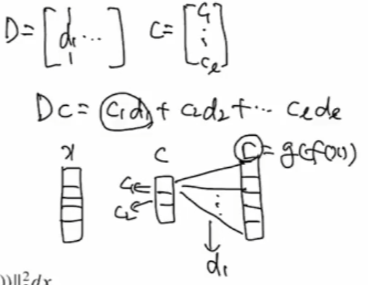
D를 열벡터행렬, 벡터 c를 c1부터 cl까지 요소를 가지는 벡터로 보면
Dc = c1d1 + c2d2 + ... + cldl이 된다. 이것을 시각적으로 표현해본다면
x를 입력값으로 encoding 벡터를 c, 출력 결과값을 r로 나타낸다. c의 벡터들이 D값에 곱해져서 더해지면 결과값 벡터가 나온다.
인코딩 함수
디코딩 함수가 위와 같이 주어졌을 때, 어떤 함수가 최적의 인코딩 함수일까? 모든 x에 대해서 x와의 차이가 최소화 되는 f(x)를 구하고자 한다.
범함수를 f(x)에 관해서 최소로 만드는 것을 변분법이라고 한다.
변분법(calculus of variations)의 방법(Euler-Lagrange 방정식)으로 풀 수 있다. 방정식
을 f에 관해 풀면 된다.
간략화를 위해서 𝑓(𝑥)=𝑐 로 두고 두면
따라서 최적의 인코더 함수는 f(x) = D^Tx
결국 인코더 함수는 디코더 함수로부터 찾아가야 한다(?)
최적의 𝐷 찾기
입력값 𝑥와 출력값 𝑔(𝑓(𝑥)) 사이의 거리가 최소화되는 𝐷를 찾는다.
에러행렬 𝐸를 다음과 정의할 수 있다.
E = X - R
우리가 찾는 최적의 𝐷는 다음과 같다. 즉 E라는 행렬의 frobenius norm을 최저값으로 만드는 D이다. 그리고 우리는 처음에 D를 정의할때 D를 직교행렬로 정의했다.
𝑅 을 다시 정리해보자
앞에서 우리는 행렬 A의 frobenius norm의 square는 A^TA의 trace의 값과 같다고 배웠다.
항을 전개하면서 XTX의 trace는 D와 상관이 없기 때문에 빼버린다. 다음으로 우리는 tr(ABC)는 그 안의 항들의 위치가 순서에 따라 바뀔 수 있다는 것을 배웠다. 그리고 정의에서 DTD가 I이므로 최종항까지 도달할 수 있게 된다!
또한 마지막 항의 주대각값의 합은 다음과 같다.
결론
