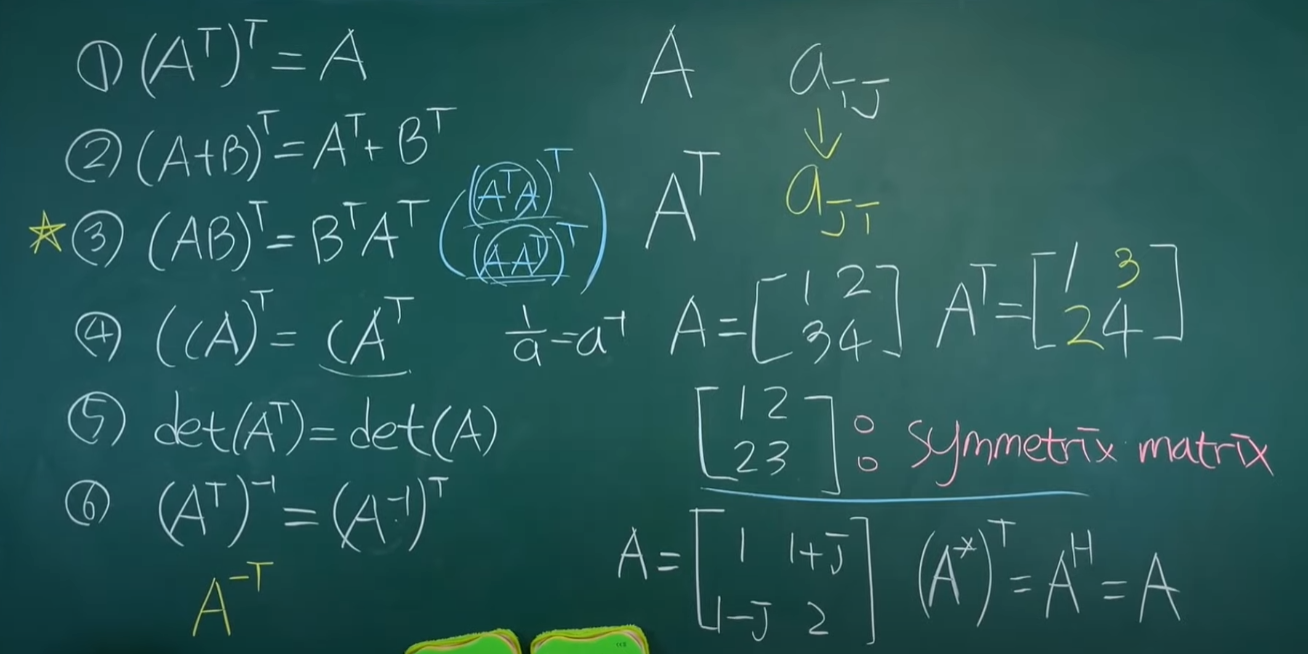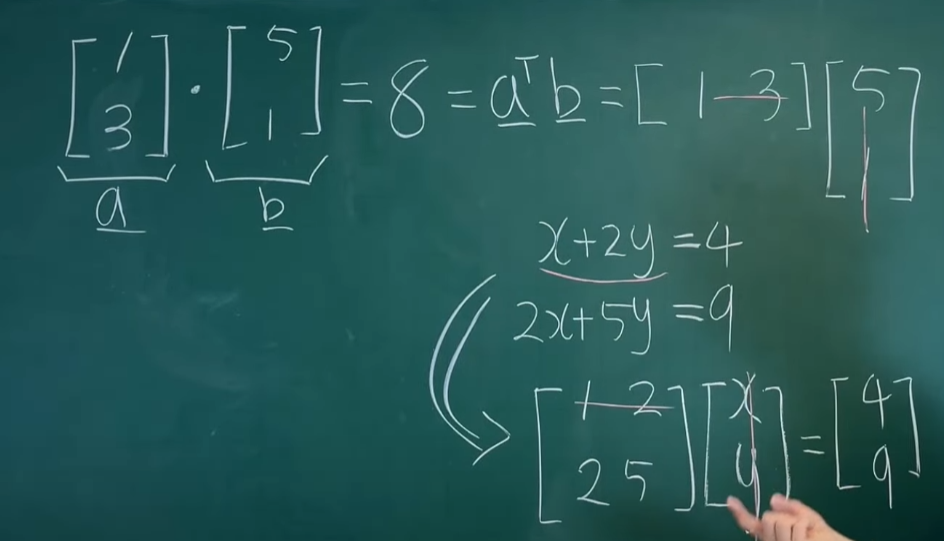[혁펜하임 선형대수학] 1강

이 내용은 혁펜하임님의 선형대수학을 공부하기 위해서 정리한 내용이며 제 정리보다는 강의가 훨씬 더 좋으므로 링크를 참고하시길 바랍니다.
https://youtu.be/7vV2SF8DyQE

선형대수학

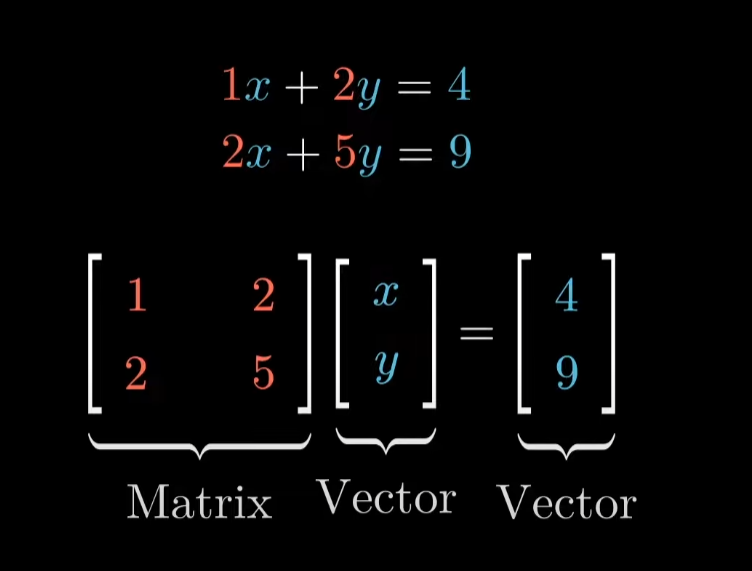
선형방정식을 다루는 수학, 행렬과 벡터에 대해서 다룬다.
결론적으로는 연립 일차방정식을 푸는 것을 목표로 한다.

행렬과 벡터

행렬과 벡터가 연립일차 방정식에서 시작했다는 것은 매우 흥미롭다.

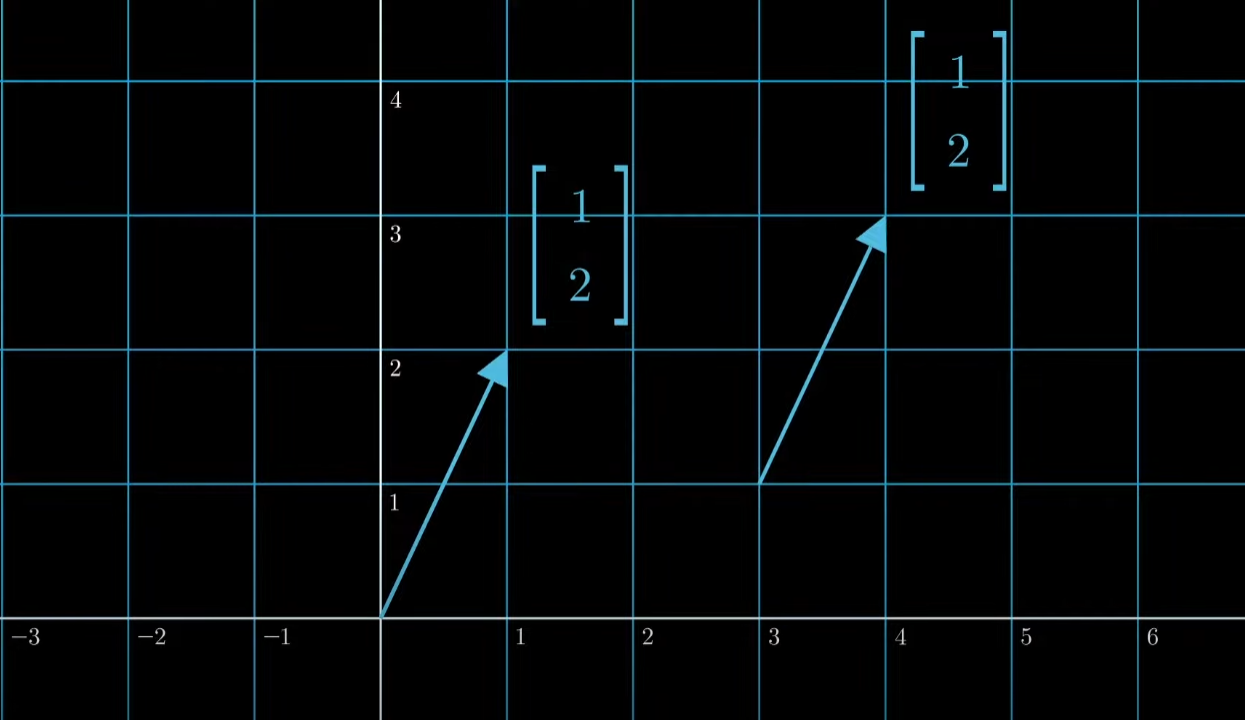
벡터

벡터는 크기와 방향이다. 따라서 크기와 방향만 유지하다면 시작하는 지점과는 무관하게 동일한 벡터이다.

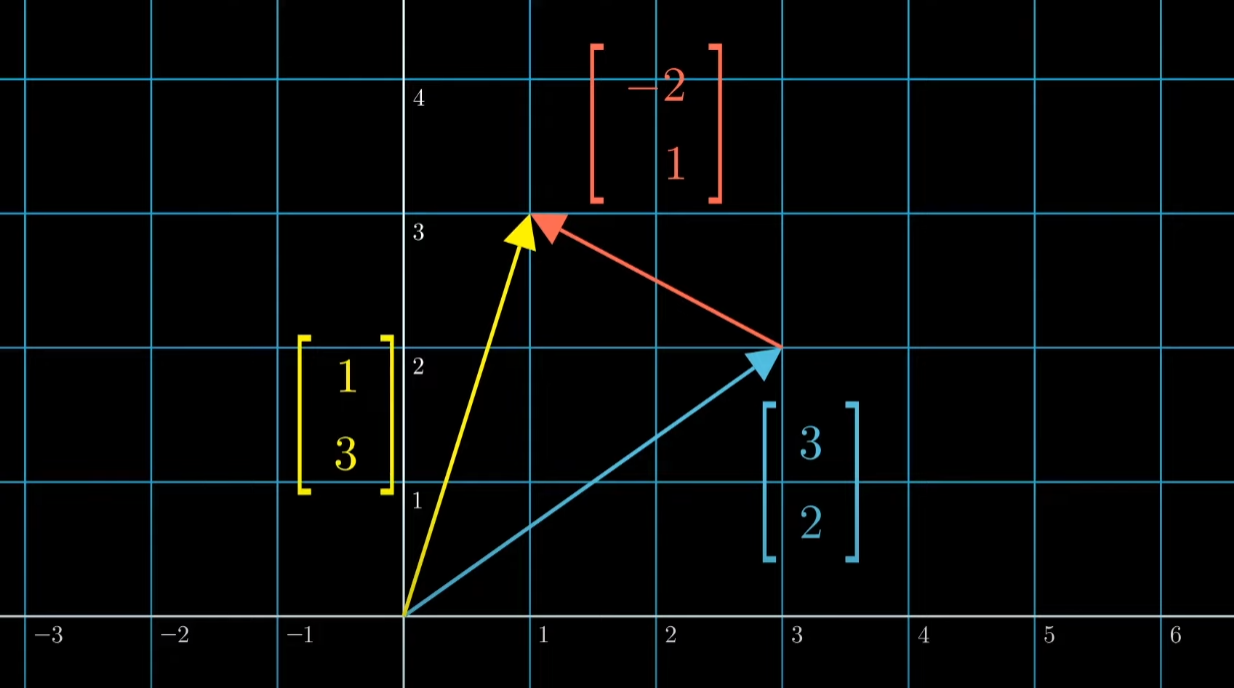
덧셈과 곱셈

벡터는 공간을 표현하는데에 사용되어질 수 있다.

전치transpose

diagonal을 유지하고 나머지들을 바꿔준다.
transpose를 했을때 자기자신이 나오는 것을 symmetric matrix라고 부른다.
3번에서 전치의 성질을 사용하면 ATA는 symmetric matrix가 되는 것을 알 수 있다.

벡터의 내적과 정사영

내적은 두 벡터 사이의 닮음의 정도를 구하는데 사용될 수 있다.

dot product는 두 벡터의 곱으로 aTb로 표현하거나 bTa로 표현할 수 있다고 한다. 이건 몰랐다.