문제
소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본이 들어있는 한 개의 파일을 만든다. 이 과정에서 두 개의 파일을 합쳐서 하나의 임시파일을 만들고, 이 임시파일이나 원래의 파일을 계속 두 개씩 합쳐서 소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고, 최종적으로는 하나의 파일로 합친다. 두 개의 파일을 합칠 때 필요한 비용(시간 등)이 두 파일 크기의 합이라고 가정할 때, 최종적인 한 개의 파일을 완성하는데 필요한 비용의 총 합을 계산하시오.예를 들어, C1, C2, C3, C4가 연속적인 네 개의 장을 수록하고 있는 파일이고, 파일 크기가 각각 40, 30, 30, 50 이라고 하자. 이 파일들을 합치는 과정에서, 먼저 C2와 C3를 합쳐서 임시파일 X1을 만든다. 이때 비용 60이 필요하다. 그 다음으로 C1과 X1을 합쳐 임시파일 X2를 만들면 비용 100이 필요하다. 최종적으로 X2와 C4를 합쳐 최종파일을 만들면 비용 150이 필요하다. 따라서, 최종의 한 파일을 만드는데 필요한 비용의 합은 60+100+150=310 이다. 다른 방법으로 파일을 합치면 비용을 줄일 수 있다. 먼저 C1과 C2를 합쳐 임시파일 Y1을 만들고, C3와 C4를 합쳐 임시파일 Y2를 만들고, 최종적으로 Y1과 Y2를 합쳐 최종파일을 만들 수 있다. 이때 필요한 총 비용은 70+80+150=300 이다.
소설의 각 장들이 수록되어 있는 파일의 크기가 주어졌을 때, 이 파일들을 하나의 파일로 합칠 때 필요한 최소비용을 계산하는 프로그램을 작성하시오.
입력
프로그램은 표준 입력에서 입력 데이터를 받는다. 프로그램의 입력은 T개의 테스트 데이터로 이루어져 있는데, T는 입력의 맨 첫 줄에 주어진다.각 테스트 데이터는 두 개의 행으로 주어지는데, 첫 행에는 소설을 구성하는 장의 수를 나타내는 양의 정수 K (3 ≤ K ≤ 500)가 주어진다. 두 번째 행에는 1장부터 K장까지 수록한 파일의 크기를 나타내는 양의 정수 K개가 주어진다. 파일의 크기는 10,000을 초과하지 않는다.출력
프로그램은 표준 출력에 출력한다. 각 테스트 데이터마다 정확히 한 행에 출력하는데, 모든 장을 합치는데 필요한 최소비용을 출력한다.https://www.acmicpc.net/problem/11066
아래 풀이과정은
https://guy-who-writes-sourcecode.tistory.com/43 를 참고하였습니다.
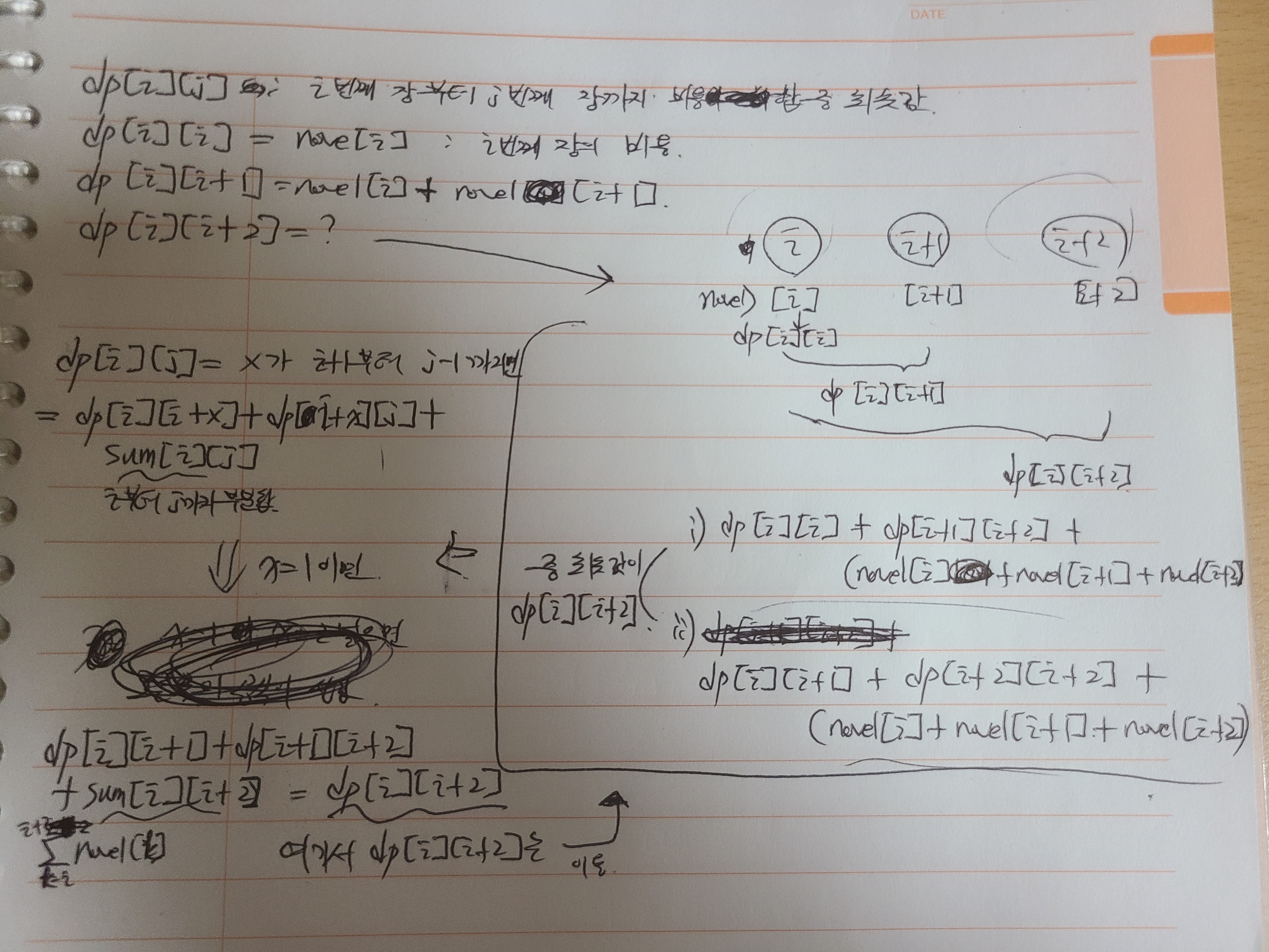
전체적인 개념은 이렇다. dp[i][j] 의 개념을 세우고, 이를 얻기위해
좀더 분할을해서 dp[i][x] + dp[x+1][j] = dp[i][j] (x+i <= x <= j-1)로 점화식을 세우고, ------------ (1)
점화식내부 의성질인 dp[i][i] 와 dp[i][i+1] , dp[i][i+2]까지의 계산이 어떻게되는지 세웠다.
(dp[i][i+3]부터는 (1) 에의해서 dp[i][i+1] + dp[i+2][i+3] 로 변환되므로, 계산필요X)
dp[i][i], dp[i][i+1] 은 간단하나 dp[i][i+2]는 두가지 계산중 하나이며, 여기서 공통점으로 i 에서 i+2 까지의 부분합이 더해진다는것이다.
따라서 sum[i]를 정의하여, sum[i+2] - sum[i-1] 을 부분합으로 계산한다.
최종적인 점화식은 dp[i][j] = ( dp[i][j] 또는, dp[i][x]+dp[x+1][j]+sum[j]-sum[i-1] 중에 최솟값) 이 된다.
이 부분에 대한 설명은 아래 사진에서

import java.util.Scanner;
public class Main {
static int dp[][];
static int novel[];
static int sum[];
static int k;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int t = scanner.nextInt();
while (t > 0) { //모든 입력을 받는다.
k = scanner.nextInt();
//테스트 마다 초기화 진행
dp = new int[k + 1][k + 1];
novel = new int[k + 1];
sum = new int[k + 1];
for (int i = 1; i <= k; i++) {
novel[i] = scanner.nextInt();
sum[i] = sum[i - 1] + novel[i]; //i번째까지의 모든 비용의 합
//부분합으로 사용할것임
}
algorithm1();
t--;
}
}
public static void algorithm1() {
//sum에 저장된수로인해 dp가완성됨
for (int n = 1; n <= k; n++) {
for (int i = 1; i + n <= k; i++) {
int j = i + n;
dp[i][j] = 214748364;
for (int x = i; x < j; x++) {
//1회째는 dp초깃값인 int최대정수와 점화식을비교, 무조건 점화식의 값이 dp[i][j]
//n회쨰는 dp[i][j] 기존값과 범위가달라진 점화식중 비교하여 최솟값이 dp[i][j]
//모든 범위를 반복시 결국 가장최솟값이 dp[i][j]
dp[i][j] = Math.min(dp[i][j],
dp[i][x] + dp[x + 1][j] + sum[j] - sum[i - 1]);
}
}
}
System.out.println(dp[1][k]);
}
}
