문제
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.
정사각형은 서로 겹치면 안 된다.
도형은 모두 연결되어 있어야 한다.
정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.
정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.
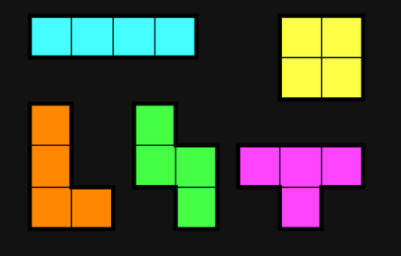
아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.
테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.
테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.
입력
첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)
둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.
출력
첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.
https://www.acmicpc.net/problem/14500
풀이
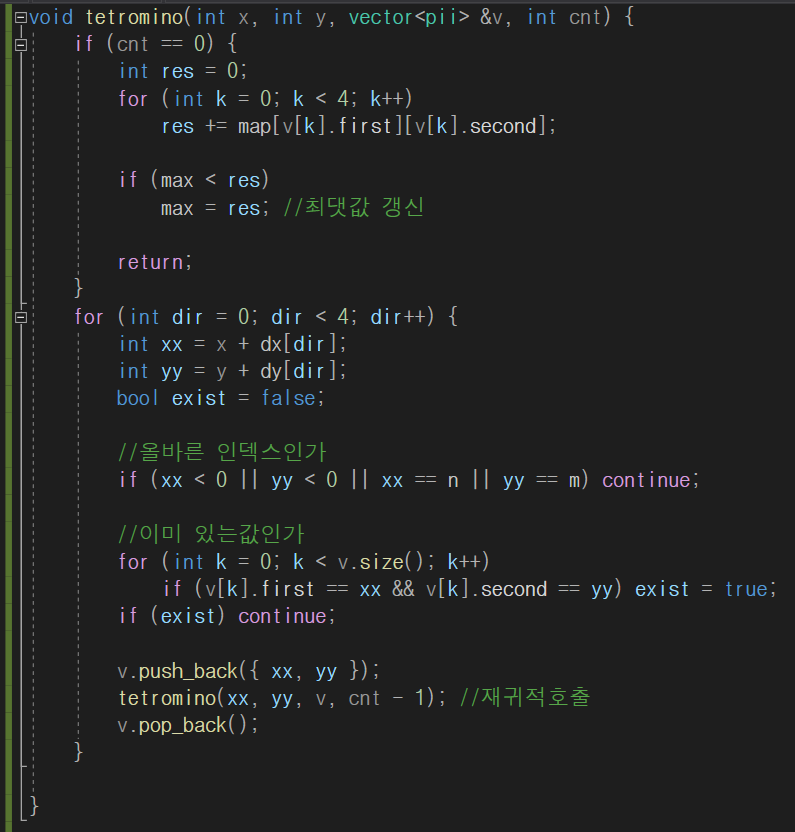
테트로미노를 대칭, 회전해도되므로, 잘생각해보면
서로 이어지는 4칸이 모두 테트로미노 인것이다. 따라서 재귀구조로
한좌표 x,y 에서 이어지는 4칸을 선택하여 그칸의 숫자합을 보면 되는 문제이다.
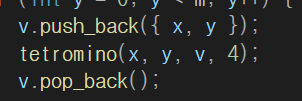
중요한점은 push_back 과 pop_back 사이에 재귀호출하는 자기함수를 끼워넣으면,
4개까지 선택하고, 다시 벡터를 비우고 다음 4개를 선택하는 구조를 만들 수 있는것.
다만, 이때 그림의 핑크색 테트로미노의 경우는 위 방법으로는 만들수가 없다. 왜냐면 위 코드는 왓던 정사각형을 다시 방문하지않으므로,
핑크색 테트로미노의경우는 왓던 정사각형을 방문하거나 아예 다른 코드를 추가해야한다.
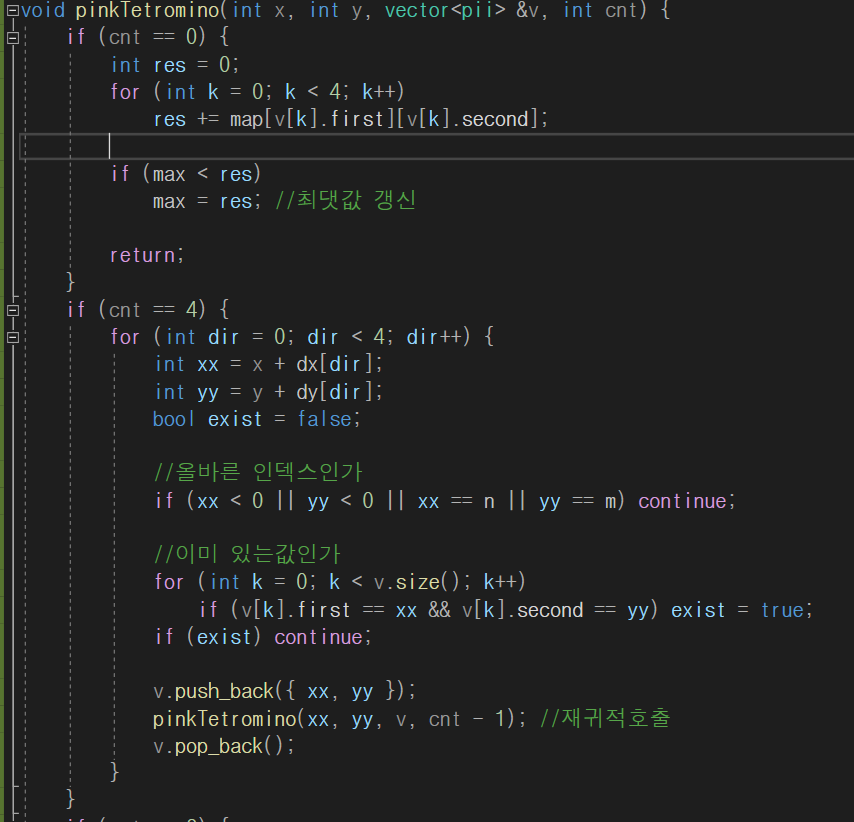
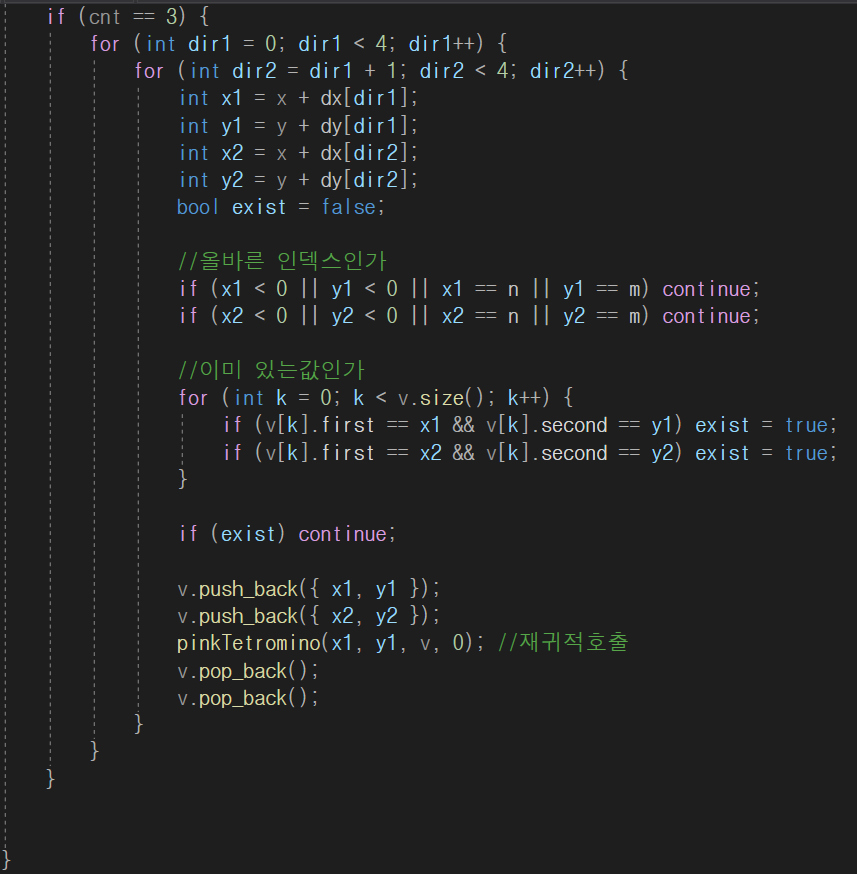
이 코드는 2개까지는 이어지게 선택하고,
그다음에 동시에 2개를 선택하여 ' ㅗ ' 모양의 테트로미노를 만들어낸다.

#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using std::vector; using std::pair;
typedef pair<int, int> pii;
int n, m, **map, max=0;
int dx[] = { 0, 1, 0, -1 };
int dy[] = { 1, 0, -1, 0 };
void init();
void func();
void pinkTetromino(int x, int y, vector<pii>& v, int cnt);
void tetromino(int X, int Y, vector<pii>& v, int cnt);
void init() {
scanf("%d%d", &n, &m);
map = new int* [n];
for (int i = 0; i < n; i++) {
map[i] = new int[m];
for (int j = 0; j < m; j++)
scanf("%d", &map[i][j]);
}
}
void func() {
vector<pii> v;
for (int x = 0; x < n; x++) {
for (int y = 0; y < m; y++) {
v.push_back({ x, y });
tetromino(x, y, v, 4);
v.pop_back();
v.push_back({ x, y });
pinkTetromino(x, y, v, 4);
v.pop_back();
}
}
printf("%d", max);
}
void pinkTetromino(int x, int y, vector<pii> &v, int cnt) {
if (cnt == 0) {
int res = 0;
for (int k = 0; k < 4; k++)
res += map[v[k].first][v[k].second];
if (max < res)
max = res; //최댓값 갱신
return;
}
if (cnt == 4) {
for (int dir = 0; dir < 4; dir++) {
int xx = x + dx[dir];
int yy = y + dy[dir];
bool exist = false;
//올바른 인덱스인가
if (xx < 0 || yy < 0 || xx == n || yy == m) continue;
//이미 있는값인가
for (int k = 0; k < v.size(); k++)
if (v[k].first == xx && v[k].second == yy) exist = true;
if (exist) continue;
v.push_back({ xx, yy });
pinkTetromino(xx, yy, v, cnt - 1); //재귀적호출
v.pop_back();
}
}
if (cnt == 3) {
for (int dir1 = 0; dir1 < 4; dir1++) {
for (int dir2 = dir1 + 1; dir2 < 4; dir2++) {
int x1 = x + dx[dir1];
int y1 = y + dy[dir1];
int x2 = x + dx[dir2];
int y2 = y + dy[dir2];
bool exist = false;
//올바른 인덱스인가
if (x1 < 0 || y1 < 0 || x1 == n || y1 == m) continue;
if (x2 < 0 || y2 < 0 || x2 == n || y2 == m) continue;
//이미 있는값인가
for (int k = 0; k < v.size(); k++) {
if (v[k].first == x1 && v[k].second == y1) exist = true;
if (v[k].first == x2 && v[k].second == y2) exist = true;
}
if (exist) continue;
v.push_back({ x1, y1 });
v.push_back({ x2, y2 });
pinkTetromino(x1, y1, v, 0); //재귀적호출
v.pop_back();
v.pop_back();
}
}
}
}
void tetromino(int x, int y, vector<pii> &v, int cnt) {
if (cnt == 0) {
int res = 0;
for (int k = 0; k < 4; k++)
res += map[v[k].first][v[k].second];
if (max < res)
max = res; //최댓값 갱신
return;
}
for (int dir = 0; dir < 4; dir++) {
int xx = x + dx[dir];
int yy = y + dy[dir];
bool exist = false;
//올바른 인덱스인가
if (xx < 0 || yy < 0 || xx == n || yy == m) continue;
//이미 있는값인가
for (int k = 0; k < v.size(); k++)
if (v[k].first == xx && v[k].second == yy) exist = true;
if (exist) continue;
v.push_back({ xx, yy });
tetromino(xx, yy, v, cnt - 1); //재귀적호출
v.pop_back();
}
}
int main(void) {
init();
func();
return 0;
}