문제
어떤 N개의 수가 주어져 있다. 그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려 한다. 만약에 1,2,3,4,5 라는 수가 있고, 3번째 수를 6으로 바꾸고 2번째부터 5번째까지 합을 구하라고 한다면 17을 출력하면 되는 것이다. 그리고 그 상태에서 다섯 번째 수를 2로 바꾸고 3번째부터 5번째까지 합을 구하라고 한다면 12가 될 것이다.
입력
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄까지 N개의 수가 주어진다. 그리고 N+2번째 줄부터 N+M+K+1번째 줄까지 세 개의 정수 a, b, c가 주어지는데, a가 1인 경우 b(1 ≤ b ≤ N)번째 수를 c로 바꾸고 a가 2인 경우에는 b(1 ≤ b ≤ N)번째 수부터 c(b ≤ c ≤ N)번째 수까지의 합을 구하여 출력하면 된다.
입력으로 주어지는 모든 수는 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.
출력
첫째 줄부터 K줄에 걸쳐 구한 구간의 합을 출력한다. 단, 정답은 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.
https://www.acmicpc.net/problem/2042
풀이
구간합을 구하는데, 변경이 빈번히 일어나는경우 세그먼트트리를 이용하면 O(logNlogM)으로 효율적으로 해결가능하다.
세그먼트트리 참고 : https://velog.io/@cldhfleks2/%EC%84%B8%EA%B7%B8%EB%A8%BC%ED%8A%B8%ED%8A%B8%EB%A6%AC
먼저, N M K받고,
세그먼트트리를 이용할것이므로 배열과 트리를 vector로 선언하고(이때, 최댓값을 고려하여 long long타입으로)크기는 N으로 초기화한다.(초기화를 안하고 사용해도 자동으로 크기를 늘려주긴한다.)트리의경우 리프노드에 배열의 원소가 들어가므로, 트리구조의 높이를 이용하여 전체 노드의 수를 구해낸다.
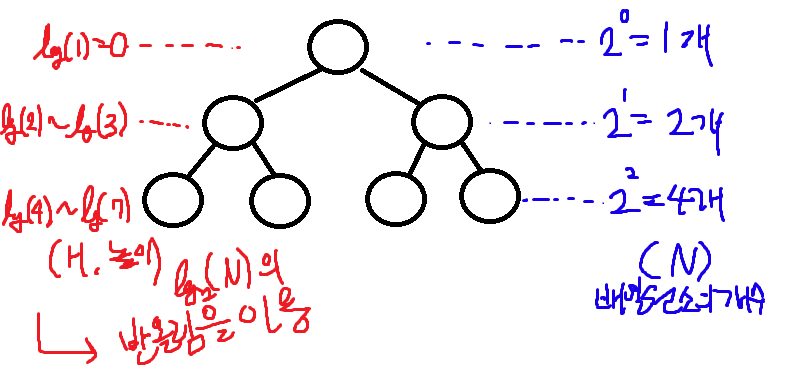
예로들면 리프노드가 3개일때 트리의 높이는 3이되어 7의 크기를 가지는데, 이는 해당높이일때 최대의 크기이므로 몇개 남지만 코드진행에는 문제가없다.(가장 마지막 리프노드하나는 아무것도 안들어간다는 뜻임)
이렇게 배열과 트리를 구현한뒤, 세그먼트트리를 만드는 함수 (makeTree)를 호출, 그다음줄부터는 a, b, c 세개정수를 받아서 a에 따른 코드를 작성해주면된다.
여기서 a==1일때 배열의원소를 변경할때 diff변수로 차이를 구하여 update함수에 넘기고,
실제 배열인 arr의원소 또한 업데이트 해주어야한다!!!!
전체코드
#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;
long long makeTree(vector<long long>& a,
vector<long long>& tree, int node, int start, int end) {
if (start == end) {
return tree[node] = a[start];
}
else {
return tree[node] =
makeTree(a, tree, node * 2, start, (start + end) / 2) +
makeTree(a, tree, node * 2 + 1, (start + end) / 2 + 1, end);
}
}
long long sum(vector<long long>& tree, int node,
int start, int end, int left, int right) {
if (left > end || right < start) {
return 0;
}
else if (left <= start && end <= right) {
return tree[node];
}
else {
return
sum(tree, node * 2, start, (start + end) / 2, left, right) +
sum(tree, node * 2 + 1, (start + end) / 2 + 1, end, left, right);
}
}
void update(vector<long long>& tree, int node,
int start, int end, int index, long long diff) {
if (index < start || index > end) return; //포함X 종료
tree[node] += diff;
//리프노드가 아닐때만 아래의 과정으로
// 모든 자식의 구간합을 변경
if (start != end) {
update(tree, node * 2, start, (start + end) / 2, index, diff);
update(tree, node * 2 + 1, (start + end) / 2 + 1, end, index, diff);
}
}
int main(void) {
//N : 개수 M : 업데이트횟수 K : 구간합횟수
int N, M, K;
scanf("%d %d %d", &N, &M, &K);
vector<long long> arr(N);
int tree_height = (int)ceil(log2(N)) + 1;
vector<long long> tree(pow(2, tree_height));
for (int i = 0; i < N; i++) {
scanf("%lld", &arr[i]);
}
makeTree(arr, tree, 1, 0, N - 1);
//N+2 줄부터
//앞숫자가 1이면 b번원소를 c로
//앞숫자가 2면 b 부터 c까지 구간합을 출력
int cnt = M + K;
while (cnt--) {
int a, b;
scanf("%d %d", &a, &b);
if (a == 1) {
long long c;
scanf("%lld", &c);
long long diff = c - arr[b-1]; //b번째
arr[b - 1] = c; // 중요
update(tree, 1, 0, N - 1, b-1, diff);
}
else if (a == 2) {
int c;
scanf("%d", &c);
//n번째이니 인덱스는 -1씩
printf("%lld\n", sum(tree, 1, 0, N - 1, b-1, c-1));
}
}
return 0;
}골드1문제지만 세그먼트트리를 구현할 줄 안다면 쉽게 풀 수 있을것이다.
