문제

마법사 상어는 그동안 배운 마법을 이용해 어항을 정리하려고 한다. 어항은 정육면체 모양이고, 한 변의 길이는 모두 1이다. 상어가 가지고 있는 어항은 N개이고, 가장 처음에 어항은 일렬로 바닥 위에 놓여져 있다. 어항에는 물고기가 한 마리 이상 들어있다. <그림 1>은 어항 8개가 바닥 위에 놓여있는 상태이며, 칸에 적힌 값은 그 어항에 들어있는 물고기의 수이다. 편의상 어항은 정사각형으로 표현했다.

어항을 한 번 정리하는 과정은 다음과 같이 이루어져 있다.

먼저, 물고기의 수가 가장 적은 어항에 물고기를 한 마리 넣는다. 만약, 그러한 어항이 여러개라면 물고기의 수가 최소인 어항 모두에 한 마리씩 넣는다. 위의 예시의 경우 물고기의 수가 가장 적은 어항에는 물고기가 2마리 있고, 그러한 어항은 2개가 있다. 따라서, 2개의 어항에 물고기를 한 마리씩 넣어 <그림 2>와 같아진다.

이제 어항을 쌓는다. 먼저, 가장 왼쪽에 있는 어항을 그 어항의 오른쪽에 있는 어항의 위에 올려 놓아 <그림 3>이 된다.

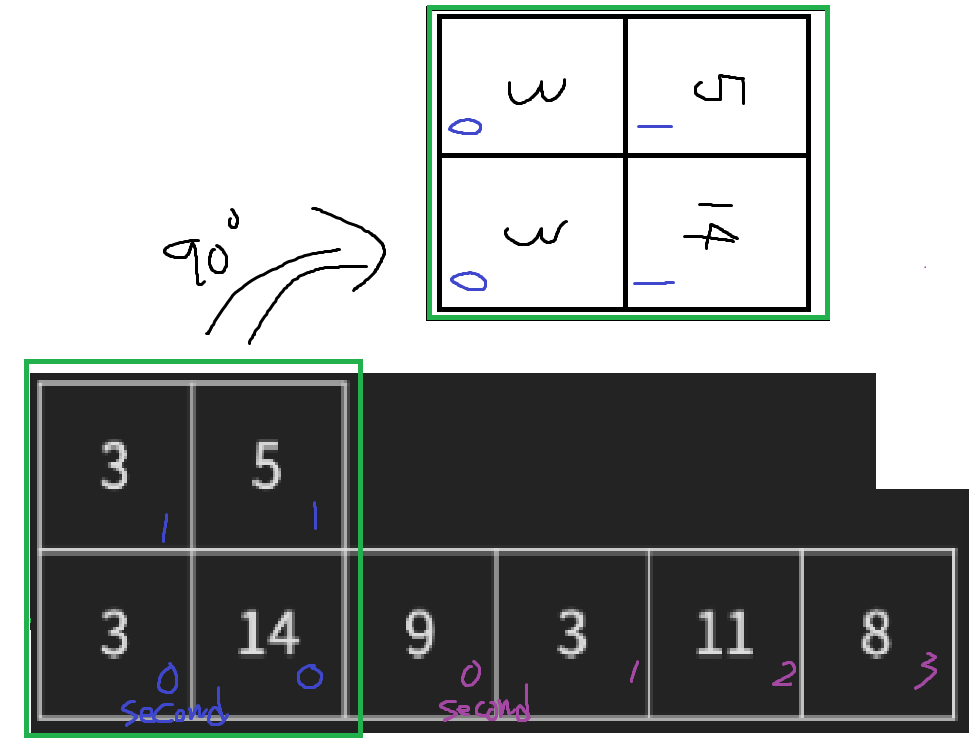
이제, 2개 이상 쌓여있는 어항을 모두 공중 부양시킨 다음, 전체를 시계방향으로 90도 회전시킨다. 이후 공중 부양시킨 어항을 바닥에 있는 어항의 위에 올려놓는다. 바닥의 가장 왼쪽에 있는 어항 위에 공중 부양시킨 어항 중 가장 왼쪽에 있는 어항이 있어야 한다. 이 작업은 공중 부양시킨 어항 중 가장 오른쪽에 있는 어항의 아래에 바닥에 있는 어항이 있을때까지 반복한다.

먼저, <그림 4>와 같이 어항이 놓인 상태가 변하고, 한 번 더 변해서 <그림 5>가 된다.

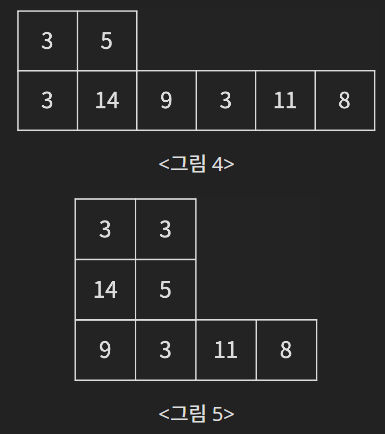
<그림 5>에서 한 번 더 어항을 공중 부양시키는 것은 불가능하다. 그 이유는 <그림 6>과 같이 공중 부양시킨 어항 중 가장 오른쪽에 있는 어항의 아래에 바닥에 있는 어항이 없기 때문이다.

공중 부양 작업이 모두 끝나면, 어항에 있는 물고기의 수를 조절한다.

모든 인접한 두 어항에 대해서, 물고기 수의 차이를 구한다. 이 차이를 5로 나눈 몫을 d라고 하자. d가 0보다 크면, 두 어항 중 물고기의 수가 많은 곳에 있는 물고기 d 마리를 적은 곳에 있는 곳으로 보낸다. 이 과정은 모든 인접한 칸에 대해서 동시에 발생한다. 이 과정이 완료되면 <그림 7>이 된다.

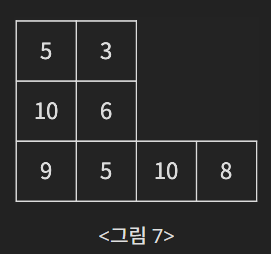
이제 다시 어항을 바닥에 일렬로 놓아야 한다. 가장 왼쪽에 있는 어항부터, 그리고 아래에 있는 어항부터 가장 위에 있는 어항까지 순서대로 바닥에 놓아야 한다. <그림 8>이 바닥에 다시 일렬로 놓은 상태이다.

다시 공중 부양 작업을 해야 한다. 이번에는 가운데를 중심으로 왼쪽 N/2개를 공중 부양시켜 전체를 시계 방향으로 180도 회전 시킨 다음, 오른쪽 N/2개의 위에 놓아야 한다. 이 작업은 두 번 반복해야한다. 두 번 반복하면 바닥에 있는 어항의 수는 N/4개가 된다. <그림 9>는 이 작업을 1번 했을 때, <그림 10>은 다시 한 번 더 했을 때이다.

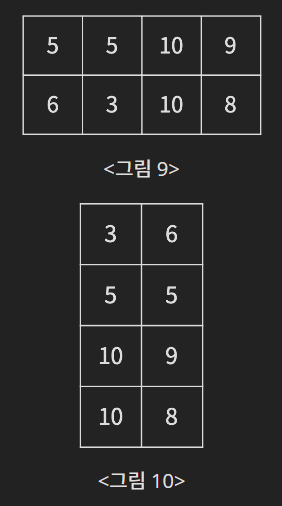
여기서 다시 위에서 한 물고기 조절 작업을 수행하고, 바닥에 일렬로 놓는 작업을 수행한다. <그림 10>에서 조절 작업을 마친 결과는 <그림 11>이 되고, 여기서 다시 바닥에 일렬로 놓는 작업을 수행하면 <그림 12>가 된다.

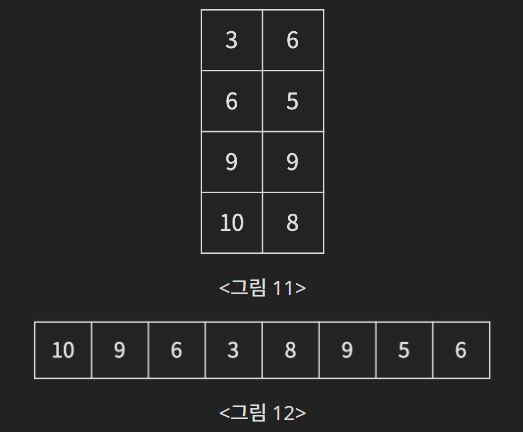
어항의 수 N, 각 어항에 들어있는 물고기의 수가 주어진다. 물고기가 가장 많이 들어있는 어항과 가장 적게 들어있는 어항의 물고기 수 차이가 K 이하가 되려면 어항을 몇 번 정리해야하는지 구해보자.

입력

첫째 줄에 N, K가 주어진다. 둘째에는 어항에 들어있는 물고기의 수가 가장 왼쪽에 있는 어항부터 순서대로 주어진다.

출력

물고기가 가장 많이 들어있는 어항과 가장 적게 들어있는 어항의 물고기 수 차이가 K 이하가 되려면 어항을 몇 번 정리해야하는지 출력한다.

제한

4 ≤ N ≤ 100
N은 4의 배수
0 ≤ K ≤ 10
1 ≤ 각 어항에 들어있는 물고기의 수 ≤ 10,000

https://www.acmicpc.net/problem/23291

풀이

문제에서 어항을 다루는 규칙이 많아서 구현할 요소가 많다.
크게 7과정으로 나눠보았다.

1. 전체 어항중 가장적은 어항에 물고기수 + 1
2. 좌측에서 2개이상쌓인 어항더미를 공중부양시켜 90도회전한뒤 우측어항더미에 쌓는다.
3. 전체어항에서 인접한 두 어항 사이에 물고기를 분배
4. 전체어항을 바닥에 일자로 펼침
5. 두번에걸쳐 좌측에서 절반씩 어항을 우측에 쌓음
6. 전체어항에서 인접한 두 어항 사이에 물고기를 분배
7. 전체어항을 바닥에 일자로 펼침

다음으로 기본 입력을 받는부분과 저장하는 컨테이너를 살펴보자.
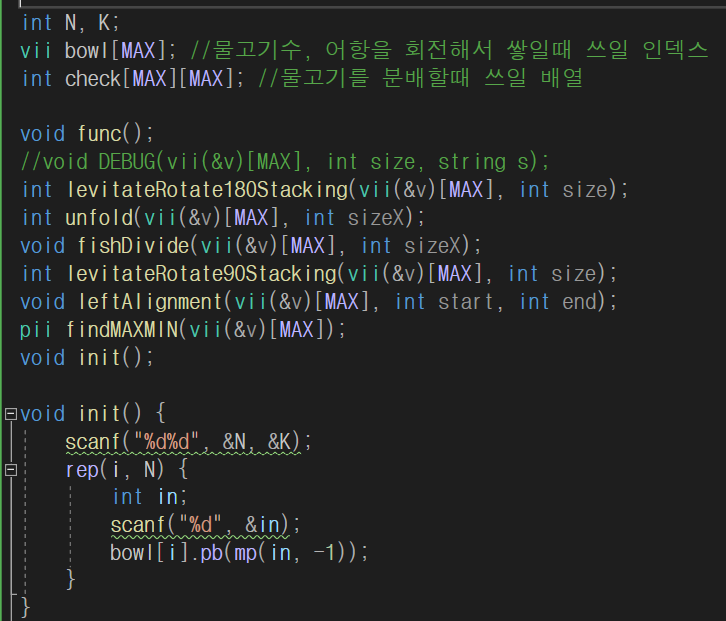bowl2배열의 first값은 물고기수 second값은 이후 쓰일 인덱스를 지정하기위한 정수값을 가진다.
처음에는 second를 사용하지않으므로 -1로 초기화시켰다.

이제 위의 1~7 과정을 자세히 살펴보자.

1. 전체 어항중 가장적은 어항에 물고기수 + 1

: 전체어항을 탐색, 최솟값에 first++;

2. 좌측에서 2개이상쌓인 어항더미를 공중부양시켜 90도회전한뒤 우측어항더미에 쌓는다.

• 좌측부터 탐색해서 2개이상 쌓인 어항 더미를 찾고, 해당 더미의 크기를 기록
• 그림처럼 파란색숫자처럼 v[i][j].second를 인덱스로 생각하여 숫자를 0부터 순차적 부여한다.
  마찬가지로 보라색숫자로 남은 어항에 second를 순차적으로 0부터 부여한다.
• 90도 회전하여 쌓는다는것은 코드로 나타내면
  방금 위에서 부여한 second값이 일치하는 v[i]에다가
  이 그림처럼 가장 우측이었던 열을 second가 같은 위치(파란색숫자 와 보라색 숫자가 같은 곳)에 push_back 한다.
  가장 우측부터 넣어야 90도 회전후 쌓은 결과가 나온다.
• 마지막으로 필자의 코드는 아래에 첨부할것인데, 필자는 옮기고나면 항상 전체어항을 왼쪽으로 정렬시키고 전체어항의 가로길이를 구했다.

3. 전체어항에서 인접한 두 어항 사이에 물고기를 분배

• 전체 어항과 같은 크기를 가지는 check배열을 만들어서 0으로 초기화 시켜둔다.
• 현재 위치가 v[i][j]일때 상하좌우로
  outOfIndex이거나 인접한 어항이 없으면 아래 과정을 진행하지 않는다.
• (인접한 어항이 있는지 확인할때는 상/하의경우 같은 v[i]간에서 간단히 구할수있으나 좌/우 의 경우 현재 j값과 양옆의 v[i-1].size()-1과 v[i+1].size()-1 를 비교하여 계산한다. 당연히 j보다 작으면 진행하지 않겠지.)
• check배열에 현재위치의 물고기가 더많을때 인접한 어항간의 물고기수 차이를 5로나는 몫을 저장해둔다 (다음위치에 +d 한만큼 현재위치에 -d 한다.)
• 마지막으로 check의 값을 v 에 모두 더한다

4. 전체어항을 바닥에 일자로 펼침

• N개의 공간을 만든뒤 idx=0 으로 둔뒤
  v[i].size()만큼 idx에 하나씩 옮기며 idx++하면 된다.

5. 두번에걸쳐 좌측에서 절반씩 어항을 우측에 쌓음

이 그림을 보며 설명하겠다. (v[i][j])

• 앞의 절반을 탐색하며 인덱스가 i일때
  v[전체길이 - i - 1]에 v[i][0]을 추가한다.
  (초록글씨, i는 오른쪽부터 왼쪽으로 추가)
• 다시 전체길이의 절반을 탐색, 인덱스가 i이면 v[전체길이 - i - 1]에 v[i][1] 먼저 추가하고 그 다음에 v[i][0]을 추가한다.
  (초록글씨, j는 뒤집에서 추가)

6. 전체어항에서 인접한 두 어항 사이에 물고기를 분배

• 3번과정과 같음

7. 전체어항을 바닥에 일자로 펼침

• 4번과정과 같음

문제에서 주어지는 입력이 그자체가 출력조건을 만족한다면 0을 출력해야하니
구하고자하는 정리횟수 res = 0으로 선언해두고,
1~7번과정을 거치기 직전에 출력조건을 만족하는지 확인하는코드를 써서 res를 출력하도록한다.
이후 1~7번을 완료하면 res++ 하도록 코드를 짜면 된다.

#define _CRT_SECURE_NO_WARNINGS 
#include <bits/stdc++.h>
#define mp std::make_pair 
#define mt std::make_tuple
#define sw std::swap;
#define ts(x) std::to_string(x)
#define tc(x) x.c_str()
#define pq std::priority_queue
#define dq std::deque
#define pb(x) push_back(x)
#define pf(x) push_front(x)
#define ppb(x) pop_back(x)
#define ppf(x) pop_front(x)
#define b(x) back(x)
#define f(x) front(x)
#define sz(x) ((int)x.size())
#define ms(a) memset((a), 0, sizeof(a)) //0으로 초기화
#define rep(i, n) for(int i = 0; i < n ; i++)
#define rrep(i, r, n) for(int i = r; i < n ; i++)
#define _rrep(i, r, n) for(int i = r; i >= n; i--)
#define each(x, a) for (auto& x: a)
#define all(x) (x).begin(),(x).end() //sort등에서 컨테이너 전체를 처리해야할때 사용
#define ct continue
#define br break
#define rt return
#define MAX 101

const int IMAX = INT32_MAX; const int IMIN = INT32_MIN;
const long long LMAX = LLONG_MAX; const long long LMIN = LLONG_MIN;
const long double PI = 3.141592653589793238462643383279502884197;
using std::vector; using std::stack; using std::queue; using std::tuple; using std::set; using std::bitset; using std::string; using std::pair; using std::greater;
using std::tie; using std::sort; using std::max_element; using std::min_element; using std::fill; using std::reverse;
//using std::max; //using std::min; //using std::map;
typedef long long ll; typedef unsigned long long ull;
typedef pair<int, int> pii; typedef pair<double, int> pdi; typedef pair<int, double> pid; typedef pair<double, double> pdd; typedef pair<int, ll> pil;
typedef pair<ll, int> pli; typedef pair<ll, ll> pll; typedef pair<ull, ull> pullull; typedef pair<int, char> pic; typedef pair<char, int> pci;
typedef pair<char, char> pcc; typedef pair<long, char> plc; typedef pair<char, long> pcl; typedef pair<ll, char> pllc; typedef pair<char, ll> pcll;
typedef pair<ull, char> pullc; typedef pair<char, ull> pcull; typedef pair<int, string> pis; typedef pair<string, int> psi; typedef pair<long, string> pls;
typedef pair<string, long> psl; typedef pair<ll, string> plls; typedef pair<string, ll> psll; typedef pair<ull, string> pulls;
typedef pair<string, ull> psull; typedef pair<string, string> pss;
typedef tuple<int, int, int> tiii; typedef tuple<int, int, int, int> tiiii;
typedef tuple<ll, ll, ll> tlll; typedef tuple<ll, ll, ll, ll> tllll;
typedef vector<int> vi; typedef queue<int> qi;
typedef vector<pii> vii; typedef queue<pii> qii;
typedef vector<pll> vll; typedef queue<pll> qll;
typedef vector<tiii> vtiii; typedef queue<tiii> qtiii;
typedef vector<tiiii> vtiiii; typedef queue<tiiii> qtiiii;
typedef vector<tlll> vtlll; typedef queue<tlll> qtlll;
typedef vector<tllll> vtllll; typedef queue<tllll> qtllll;
template <class T> inline T sq(T num) { rt num * num; }//제곱함수
template <class T> inline T GCD(T num1, T num2) { if (num2 == 0) rt num1; rt GCD(num2, num1 % num2); }
template <class T> inline T LCM(T num1, T num2) { if (num1 == 0 || num2 == 0) rt num1 + num2; rt num1 * (num2 / GCD(num1, num2)); }
//pii operator - (pii a, pii b) { return pii(a.first - b.first, a.second - b.second); }

int N, K;
vii bowl[MAX]; //물고기수, 어항을 회전해서 쌓일때 쓰일 인덱스
int check[MAX][MAX]; //물고기를 분배할때 쓰일 배열

void func();
//void DEBUG(vii(&v)[MAX], int size, string s);
int levitateRotate180Stacking(vii(&v)[MAX], int size);
int unfold(vii(&v)[MAX], int sizeX);
void fishDivide(vii(&v)[MAX], int sizeX);
int levitateRotate90Stacking(vii(&v)[MAX], int size);
void leftAlignment(vii(&v)[MAX], int start, int end);
pii findMAXMIN(vii(&v)[MAX]);
void init();

void init() {
    scanf("%d%d", &N, &K);
    rep(i, N) {
        int in;
        scanf("%d", &in);
        bowl[i].pb(mp(in, -1));
    }
}

//v의 최댓값 최솟값을 리턴
pii findMAXMIN(vii (&v)[MAX]) {
    int max = IMIN;
    int min = IMAX;
    rep(i, N) {
        int element = v[i][0].first;
        if (max < element) max = element;
        if (min > element) min = element;
    }

    rt mp(max, min);
}

//어항을 왼쪽정렬한다.
//start ~ end-1 인덱스까지의 모든 어항을 전부 좌측으로 옮김
//실제크기는 end - start
//옮긴후 0 ~ (end-start)-1 인덱스로 정렬될것
void leftAlignment(vii(&v)[MAX], int start, int end) {
    //1. 좌측으로 옮김
    int left = 0;
    rrep(i, start, end) { //start인덱스부터 left에 쌓음
        v[left] = v[i]; //복사
        left++;
    }

    //2. 우측에 남은것을 지움
    rrep(i, left, end)  //우측에 기존에있던 어항을 지움
        v[i].clear();
}

//좌측 쌓여진 어항을 공중부양시킨뒤 회전후 우측어항위에 쌓는 함수
//size : 전체 어항의 가로 길이
//완성뒤 전체 어항의 가로 길이를 리턴
int levitateRotate90Stacking(vii (&v)[MAX], int size) {
    int widthSize = size; //전체 어항들의 가로 길이

    while (1) {
        //1. 공중부양 시킬 좌측 어항더미(최소2개이상 쌓인 어항들)를 선택
        int right = -1; //공중부양시킬 열인덱스중 가장 오른쪽것
        int chooseSize;
        rep(i, N) 
            if (v[i].size() >= 2)
                right = i;
            else
                br; //좌측 어항더미는 연속되있으므로.. 쌓여지지않은 어항을 만나면 종료
        chooseSize = right + 1;

        //2. 선택한 어항더미에 인덱스(second값)를 부여함
        //어항더미들의 쌓여진 최대높이를 구해놔야함(4번에서 쓰임)
        int chooseHeightSize = -1; //90도 돌렸을때 어항더미들의 가로 최대 길이.
        rep(i, chooseSize) {
            if (chooseHeightSize < sz(v[i])) chooseHeightSize = sz(v[i]);
            rep(j, sz(v[i]))
                v[i][j].second = j; //해당열의 쌓아진순서대로 0, 1, 2, 3..
        }

        //3. 나머지 어항들의 길이계산
        int remainingSize = widthSize - chooseSize;

        //4. 어항더미를 위에 쌓을 수 없다면 중단
        if (chooseHeightSize > remainingSize) {
            //모든 어항의 second값을 -1로 초기화후 중단
            rep(i, remainingSize) 
                rep(j, sz(v[i]))
                v[i][j].second = -1;
            br; 
        }

        //5. 나머지 어항들(열)에 인덱스를 부여함
        int maxIndex = -1;
        int idx = 0; //왼쪽부터 0, 1, 2, 3..
        rrep(i, right + 1, widthSize) {
            rep(j, sz(v[i])) {
                v[i][j].second = idx; 
            }
            idx++;
        }
        idx = 0;

        //6. 공중부양시키고 90도 회전한 어항을 나머지 어항위에 쌓기
        //공중부양시킨 더미 i
        //v[i][j].second를 idx로, 
        //v[i][j].second이 같은곳에 쌓음 된다.
        //right -> 0 역순으로 쌓아야함. 
        _rrep(i, right, 0) {
            rep(j, sz(v[i])) {
                int value = v[i][j].first; //물고기수
                idx = v[i][j].second; //인덱스
                v[chooseSize + idx].pb(mp(value, -1)); //second는 이제 초기화할 값임
            }
        }

        //7. 이동시킨후 기존에있던 자리의 어항더미들을 삭제
        //0 ~ right까지 어항을 전부 삭제
        rep(i, right + 1) v[i].clear();

        //8. 전체 어항을 좌측정렬
        //right + 1 ~ bottomSize - 1까지
        leftAlignment(v, right + 1, widthSize);

        //9. 모든어항의 second값을 -1로 초기화
        rep(i, remainingSize)
            rep(j, sz(v[i])) 
                v[i][j].second = -1;

        //10. 전체어항의 가로길이를 다시 구함
        widthSize = remainingSize;
    }

    rt widthSize;
}

//모든인접한 어항간의 물고기 분배
int dxy[][2] = { {0, 1}, {0, -1}, {-1, 0}, {1, 0} };
void fishDivide(vii (&v)[MAX], int size) {
    int sizeX = size;
    rep(i, MAX)
        ms(check[i]); //전체 초기화

    //1.두 인접어항의 분배해야할 물고기수를 check에 저장
    rep(i, sizeX) {
        int sizeY = sz(v[i]);
        rep(j, sizeY) {
            rep(dir, 4) {
                int x = i + dxy[dir][0]; //인접한 어항의 좌표
                int y = j + dxy[dir][1];
                int d; //두 어항의 물고기수 차이를 5로나눈 몫 
                int gap; //인접한어항과의 물고기수 차이 v[현재] - v[인접]이 양수여야함

                //1-1. x,y위치가 잘못된 인덱스거나 어항이 존재하지않으면 제외
                //위쪽 : 현재 어항이 가장 상단에 있으면 인접한 어항이 없음
                //아래쪽 : 현재 어항이 가장 하단이면 인접한 어항이 없음
                //왼쪽 : 현재 어항이 가장 좌측에 있으면 인접한 어항이 없음, 바로 왼쪽에 어항이 쌓인높이가 j이상 되어야 물고기 분배가능
                //오른쪽 : 위와 동일(방향만 오른쪽)
                if (x == -1 || y == -1 || x == sizeX || y == sizeY) ct;
                if ( (dir == 2 || dir == 3) && (j > sz(v[x]) - 1) ) ct; //옆의 어항의 높이가 현재 어항의 높이보다 낮으면 없는것

                gap = v[i][j].first - v[x][y].first; 
                d = gap / 5;
                if (gap > 0) { //물고기수가 더많은데서 더적은데로만 옮긴다.
                    check[i][j] -= d; //현재위치에서 물고기를빼서
                    check[x][y] += d; //인접한 어항에 분배
                }
            }
        }
    }

    //2. 계산한 분배수를 실제 어항에 적용
    rep(i, sizeX) {
        int sizeY = sz(v[i]);
        rep(j, sizeY) {
            v[i][j].first += check[i][j]; //위에서 계산한 물고기 분배갯수를 실제로 적용
        }
    }
}

//어항을 모두 평평하게 펼친다.
//완성후 어항의 가로길이 리턴
int unfold(vii (&v)[MAX], int sizeX) {
    vii res[MAX];
    int idx = 0; //바닥에 놓여질 위치 인덱스

    //1. res에 어항을 펼친다.
    rep(i, sizeX) {
        int sizeY = sz(v[i]);
        rep(j, sizeY) {
            res[idx].pb(v[i][j]); //idx위치로 옮김
            idx++;
        }
    }

    //2. 원래 있던 모든 어항을 없앰
    rep(i, sizeX)
        v[i].clear();

    //3. 펼쳐진 어항들을 res에서 v로 옮김
    rep(i, idx)
        v[i].pb(res[i][0]);

    rt idx;
}

//절반을 떼서 180도 회전후 쌓고 다시 절반을떼서 180회전후 다시 쌓음
//완성뒤 전체 어항의 가로길이 리턴
int levitateRotate180Stacking(vii (&v)[MAX], int size) {
    int widthSize = size;

    //1. 절반을 선택해서 나머지 절반위에 180도 회전후 쌓음
    int halfSize = widthSize / 2;
    rep(i, halfSize) {
        //i -> (widthSize-i-1)열에 추가
        v[widthSize - i - 1].pb(v[i][0]);
    }

    //2. 좌로 정렬
    leftAlignment(v, halfSize, widthSize);
    widthSize = halfSize; //전체크기 다시 계산

    //3. 다시 절반을 선택해서 나머지 절반위에 180도 회전후 쌓음
    halfSize = widthSize / 2;
    rep(i, halfSize) {
        //좌측 절반 어항더미중
        //맨위 어항한줄을 옮기고 그다음 바닥 어항한줄을 옮김
        //i -> (widthSize-i-1)열에 추가
        v[widthSize - i - 1].pb(v[i][1]); //맨위 어항
        v[widthSize - i - 1].pb(v[i][0]); //바닥 어항
    }

    //4. 좌로 정렬
    leftAlignment(v, halfSize, widthSize);
    widthSize = halfSize;

    rt widthSize;
}

//void DEBUG(vii (&v)[MAX], int size, string s) {
//    printf("%s\n", tc(s));
//    int maxY = 0;
//    rep(i, size)
//        if (maxY < sz(v[i])) maxY = sz(v[i]);
//
//    _rrep(j, maxY-1, 0) {
//        rep(i, size) {
//            int sizeY = sz(v[i]);
//            if(j > sizeY - 1)
//                printf("     ");
//            else
//                printf("%3d  ", v[i][j].first);
//        }
//        printf("\n\n");
//    }
//}

void func() {
    int res = 0; //어항정리 횟수
    while (1) { //어항정리하자
        int widthSize = N;
        int max, min;
        tie(max, min) = findMAXMIN(bowl);
        if (max - min <= K) br;

        //1. 최솟값인 어항에 물고기 + 1
        rep(i, N)
            if (min == bowl[i][0].first)
                bowl[i][0].first++;

        //2. 어항을 쌓아올림
        //2-1. 가장좌측 어항 하나를 그 오른쪽 어항위에 쌓음
        int value = bowl[0][0].first; //어항의 물고기수
        bowl[1].pb(mp(value, -1)); //그 오른쪽 어항위에 쌓음
        bowl[0].clear(); //옮겼으니 기존위치의 어항을 비움

        //2-2. 쌓고난뒤 어항을 좌로정렬
        //총 N-1개의 어항을 0번인덱스부터 시작하도록 옮길것
        leftAlignment(bowl, 1, widthSize);
        widthSize -= 1;

        //2-3. 어항을 좌측부터 최소2개이상 쌓아진 더미를 회전시켜서 쌓아올림
        //N-1개의 어항..(가로길이)
        widthSize = levitateRotate90Stacking(bowl, widthSize);

        //3. 물고기수 조절
        fishDivide(bowl, widthSize);

        //4. 쌓여있는 어항들을 바닥에 일자로 펼친다.
        widthSize = unfold(bowl, widthSize) ;

        //5. 두번에걸쳐 절반씩 좌측에 우측에 쌓음
        widthSize = levitateRotate180Stacking(bowl, widthSize);

        //6. 다시 물고기수 조절
        fishDivide(bowl, widthSize);
  
        //7. 다시 쌓여있는 어항들을 바닥에 일자로 펼친다.
        widthSize = unfold(bowl, widthSize);

        res++; //찾고자하는 어항 정리 횟수
    }

    printf("%d", res);
}

int main(void) {
    init();
    func();

    rt 0;
}