import java.util.Scanner;
public class Main {
//dp는 코어정사각형으로 만들어질수있는 정사각형의갯수를 저장. (이정사각형은 마름모이거나 아니거나 두가지를 의미.)
//dp[i][j] i 는 ixj 크기의 격자안에서 가질수있는 모든 크기의 코어 정사각형으로 만들어지는 정사각형 갯수를 저장.
//코어정사각형의 크기는 0x0 , 1x1 , 3x3 , 5x5 , '' 이다.
//예로들어 dp[5][5] 는 (5x5인 코어정사각형이 만드는 정사각형갯수) + (3x3 '') + (1x1 '') + (0x0 '')이다.
//직사각형일 경우도 있다. square 메소드에서 알아서 처리함~!
//코어정사각형의 한변의 길이를 A, 이보다 +2인 해당코어정사각형으로 만들어지는 홀수정사각형의 크기를 B라고하면
//코어정사각형으로 만들어지는 정사각형들의갯수는 (A/2 + 1)*2 개
//즉 ((B-2)/2 + 1)*2 개 이다.
private static long dp[];
private static long box[];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
dp = new long[100001];
box = new long[100001];
//코어가 0이면 1x1 크기의 마름모x인정사각형만나옴. 이 정사각형의 총갯수는 m x n 갯수랑 같겠지.
dp[0] = 1;
dp[1] = 1;
dp[2] = 1;
dp[3] = 2;
dp[4] = 2;
box[0] = 1;
box[1] = 1;
box[2] = 4;
while(true) {
int m = scanner.nextInt();
int n = scanner.nextInt();
if(m == 0 && n == 0)
break;
System.out.println(square(m, n));
scanner.nextLine();
}
scanner.close();
}
private static long square(int m, int n) {
if(m == 1 && n == 1)
return dp[1];
//가장쉬운경우의수 1
if(m == 1 || n == 1)
return m*n;
//가장쉬운경우의수 2
if(m == 2 || n == 2)
return m*n;
//m x n 격자에 포함되는 가장작은 정사각형의 한변의길이.
int min_square = Math.min(m , n);
int max_square = Math.max(m , n);
//마름모정사각형은 코어 정사각형(1x1 , 3x3 , 5x5 , ''')으로 만든다.
//코어정사각형으로 나오는 마름모정사각형 갯수에 곱해질 값.
int square_bowl = (m-1)*(n-1);
//마름모x정사각형을 위한 격자 전체 사이즈 이또한 곱해질 값.
int size = m*n;
//밑에 for문돌아가면서 i값에따른 코어정사각형한개가 만드는 정사각형갯수
//즉 ((B-2)/2 + 1)*2 개 이다.
int square_all = 0;
//격자를 정사각형으로 만 생각해서 먼저만들자.
//코어정사각형의 한변의 길이를 A, 이보다 +2인 해당코어정사각형으로 만들어지는 홀수정사각형의 크기를 B라고하면
//코어정사각형 하나로 만들어지는 정사각형들의갯수는 (A/2 + 1)*2 개
//즉 ((B-2)/2 + 1)*2 개 이다.
//여기서 B는 (0x0) , (1x1) , (3x3) , (5x5) , '' 이다.
int sub = 0;
long temp1 = 0;
long temp2 = 0;
long temp3 = 0;
if (m != n) {
sub = Math.subtractExact(max_square, min_square);
temp1 = (1 + sub);
temp2 = (4 + 2*sub);
temp3 = 0;
}
//결과출력용.
long result = 0;
//격자내에 가장큰 정사각형의 dp값이 구해진경우.
boolean[] check = new boolean[min_square + 2];
for (int i = 3; i <= min_square; i++) {
//b는 현재 i가 홀수면 b = i
//i 가 짝수면 b = i-1
int b = 0;
// i가 짝수면
if (i % 2 == 0) {
// ex) i=4 => b=3
b = i / 2 + 1;
} else {
// i가 홀수면
// ex) i=3 => b=3
b = i;
}
//마름모제외한 일반 정사각형갯수를 셈. (격자가 정사각형일때. 격자가 직사각형이면 여기갯수에 추가로 곱하면됨)
if (box[i] == 0) {
// 마름모아닌 정사각형갯수
box[i] = i * i + box[i - 2];
}
if (m != n) {
temp3 = i * (i + sub) + temp1;
temp1 = temp2;
temp2 = temp3;
}
// 또한 i가 홀수일때만. dp는 홀수만담음.
if (dp[i] == 0 && i%2 != 0) {
// 코어정사각형의 한변의 길이
int a = b - 2;
// 이전의 코어정사각형( 현재 코어정사각형보다 한변길이가 2 작은것 )로 만들어진 갯수 + 현재 코어정사각형이 만드는갯수)
dp[i] = ((b-2) / 2 + 1) * 2;
//i+1번째, 짝수번째가 존재하면 추가.
if(i+1 <= min_square)
dp[i+1] = dp[i];
}
System.out.println("dp[" + i + "]:" + dp[i]);
//i가 홀수일때만 result 에 더함.
if (check[i] == false)
result += ((m - b + 1) * (n - b + 1)) * dp[i];
if (i % 2 != 0) { //홀수일때 check을 할거임.
check[i] = true; //현재 i
check[i + 1] = true; // ex) i=3 이면 i=4 일때 이미 i=3에서 계산했으니 계산방지를위해
// i + 1 인 i =4 일때도 check.
}
}
if (m == n) {
System.out.println("result : " + result + " , box : " + box[m] + " , dp : " + dp[m]);
return result + box[m];
} else {
System.out.println("result : " + result + " , box(temp) : " + temp3 + " , dp : " + dp[m]);
return result + temp3;
}
}
}현재 백준사이트에서는 틀리다고나오지만 아무리 계산해봐도 답이나온다.
1 x 1 일때 1개..부터 m x n 이 정사각형일때, 직사각형일때 나누어 계산했다.
분명 안나누고 하나로 통합하는 공식이있을건데 일단..
사용된요소들 :
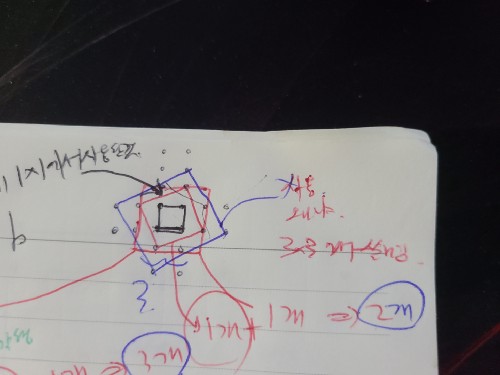
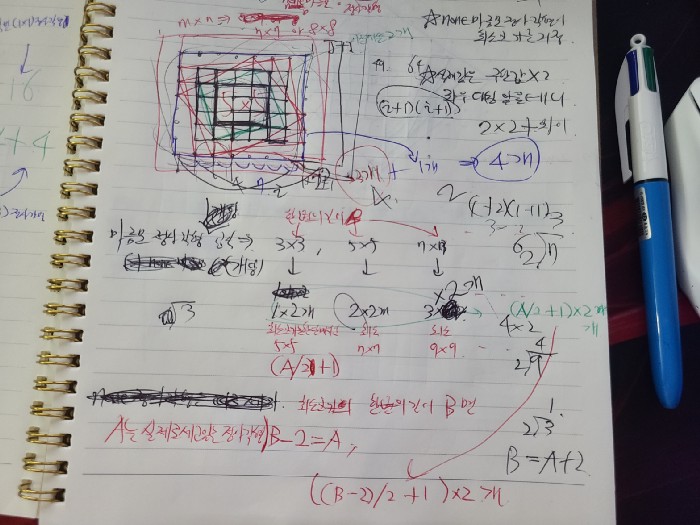
dp[i] : i과같거나 하나작은 홀수가 있을때, i x i 칸안에 들어가는 마름모(격자에 수직,수평한 올바른 정사각형을 제외한것)의 갯수이다.
ex)d[3] = 3x3격자안에 생길수있는 마름모로는 2개가있다.(위 사진 에서 빨간색이 i의 변의 크기, b라고 칭하며 검은색선의 변의크기를 a라고 칭하겠다.)
즉 3x3 크기를 넘지않는 마름모갯수이다.
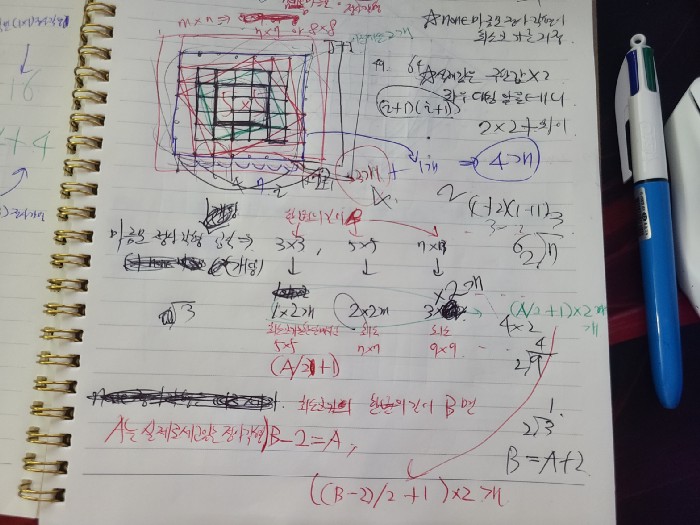
따라서 수식은 dp[i] = ((i-2)/2 + 1)*2;
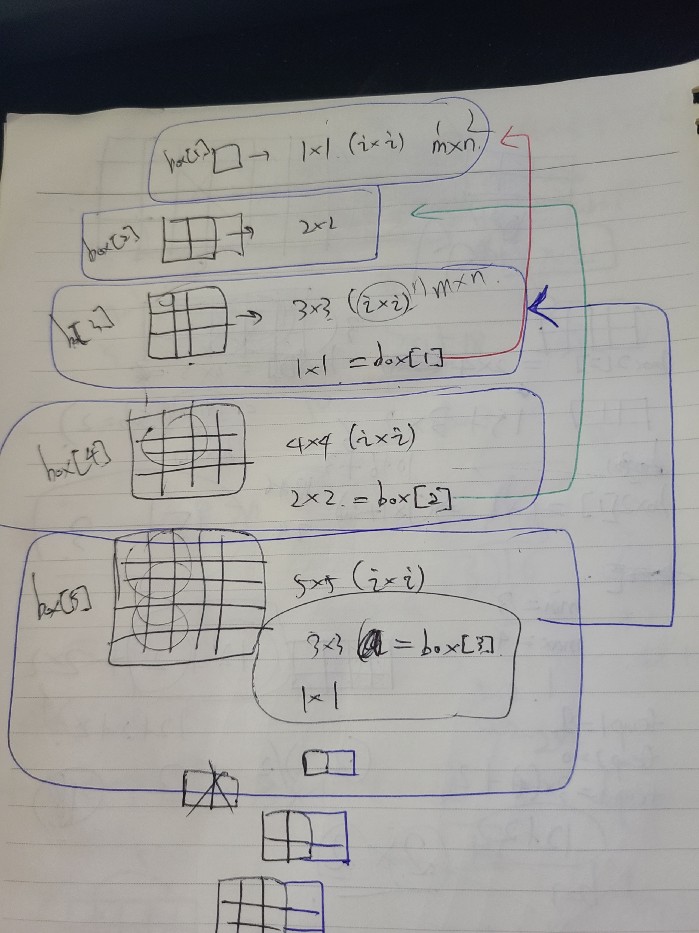
box[i] :i x i칸에서, 위의 dp[i]를 제외한 격자에 수직수평한 홀수인 정사각형들의 갯수이다.
ex) box[1] = 1 , box[3] = 10 이다.
정사각형에서는 box[i]=ii + box[i-2];
일반 직사각형에서는 temp3(i) , temp2(i-1), temp1(i-2) 의개념으로 temp3 = i(i + sub) + temp1 이다.(여기서 sub 는 m과n의 차이값) 왜 이렇게 구분하냐면 box를 이차원배열로 생성하자니 메모리가 부족하고 1차원으로 는 설명이안되기때문에 차라리 시간자원을 쓰기로했다.
직사각형일경우는 따라서 격자가 정사각형이면 동적프로그래밍, 직사각형이면 순차적인 프로그래밍이된다.
check[i] : boolean 값을 가진배열로, 위에서 사용한 i 가 홀수일때만작동함을 인지시키기위해 사용한다. 즉 짝수일때는 동적프로그래밍으로 dp를 사용하여 결과값(여기서는 result)을 늘리지않는다.
재귀 함수꼴은아니고 메모리생성수순을 메모이제이션을활용한 동적프로그래밍만 사용했다. 자세한 설명은 코드에 주석으로 표기하였다.
문제는 이게 답은나오는데왜 백준사이트에서는 답으로 표기안되는지..