활용 목적

어떠한 입력 시퀀스가 있다고 하자. 입력 시퀀스는 시계열 데이터 혹은 특정 차원으로 uniform sampling된 신호이다. 만약, non-uniform sampling을 사용한다면 적절한 위치에 0을 삽입하면 된다. 여기서 우리는 편의상 입력 시퀀스를 시계열 데이터라고 하자.

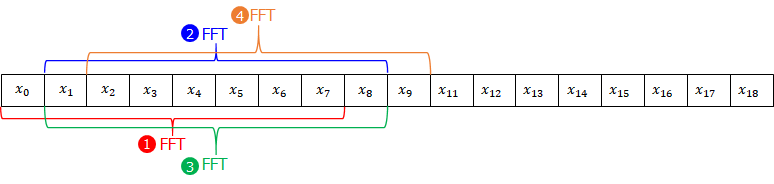
우리의 목적은 아래 그림과 같이 주어진 입력 시퀀스의 주파수 성분의 변화를 매 샘플링 시간 간격으로 관찰하는 것이다. 즉, short-time Fourier transform (STFT)을 통해 주파수 변화를 관찰하고자 하는 것이다. 이 경우 FFT window를 shift하면서 FFT 알고리즘을 적용하는 것이 단연 연산 복잡도면에서 효율적이라고 할 수 있다. 그러나 특정 주파수 영역만 관심 대상일 경우, FFT를 통해 전체 스펙트럼을 관찰하는 대신 일부 스펙트럼 영역만 낮은 연산량으로 관찰할 수 있으며, 이를 sliding DFT라 부른다.

Sliding DFT

다음과 같이 $n$번째 샘플링 시간에 $N$개의 샘플이 주어졌다고 하자.

DFT의 정의에 의해 $\mathbf{x}(n)$의 $k$번째 bin의 DFT 출력 값은 다음과 같다. ($단, m\leftarrow n-N+1$)

이때, 다음 샘플링 시간에 $x(n+1)$이 새로이 입력되었다고 해보자. 그러면 FFT의 윈도우 길이는 $N$이므로 $x(n)$의 첫 번재 샘플링 $x(n-N+1)$을 버리고 다음과 같이 FFT 입력 신호가 변하게 된다.

식 (3)과 식 (1)을 비교해보면 FFT 입력관점에서 오래된 샘플 하나를 버리고 새로운 샘플 하나를 추가하였다. 즉, FFT 입력단에서 모든 정보가 새로이 대체된 것이 아니다. 따라서 새로 추가된 정보를 이용하여 이전 계산 결과를 보정함으로써 식 (3)에 대한 FFT를 수행하는 대신 우리가 관심있는 특정 주파수 인덱스 $k$에 대한 주파수 응답 $X(k)$를 구할 수 있다. 이를 위해 다음과 같이 두 가지 단계를 거친다.

1. oldest sample을 new sample로 대체

$x(n+1)$이 새롭게 주어졌을 때, 식 (1)의 $x(n-N+1)$을 $x(n+1)$로 대체한다.

DFT 연산 시 가장 오래된 샘플 $x(n-N+1)$은 식 (2)에서 $m=0$이므로 항상 1과 곱해진다. 따라서 식 (4)에 FFT를 적용하여 $X_{n+1}(k)$를 구한 결과는 다음 수식과 완전히 등가이다.

2. Circular shift property 적용

우리는 식 (4)가 아니라 식 (3)의 FFT 응답을 얻고자 한다. 식 (3)과 식 (4)를 비교해보면 식 (4)를 좌측으로 한 샘플 circular shift한 것과 같다. DFT의 circular shift property에 의해 FFT 입력 샘플을 좌측으로 한 번 시프트하는 것은 주파수 영역에서 각 샘플에 $\exp(j2 \pi k/N)$만큼 위상 회전을 적용하는 것과 같다. 따라서 최종적으로 다음과 같은 결론을 도출할 수 있다.

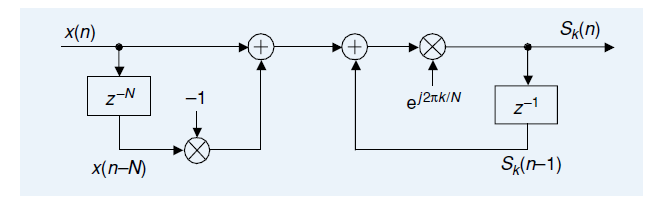
IIR Filter 형태로 구현

식 (6)의 구현은 다음과 같이 간단한 IIR 필터 형태로 구현할 수 있다. 아래 그림은 인터넷에 떠보는 강의노트에서 가져온 것이다. 출처를 명시하려고 하였는데 URL을 다시 찾을 수 없어 생략한다. 참고로 동일한 그림을 다음 논문에서도 확인할 수 있다.

E. Jacobsen and R. Lyons, "The Sliding DFT," IEEE Sig. Pro. Mag, vol. 20, no. 2, pp. 74-80, Mar. 2003.