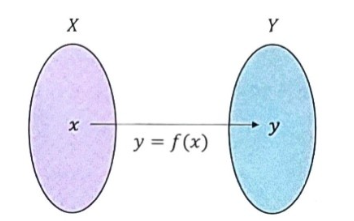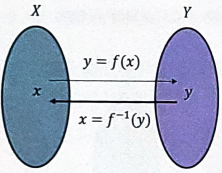초록색과 같은 색상의 Keyword 는 한번 쯤 읽어볼만한 소재입니다.노란색과 같은 색상의 Keyword 는 꼭 알아두어야 할 소재입니다.파란색과 같은 색상의 Keyword 는 부가설명입니다.마지막으로 Game Math 글의 모든 Image 출저는 '이득우의 게임 수학' 임을 밝힙니다.
° Function
두 Set 에서 첫 번째 Set 의 모든 Element 가 빠짐없이
두 번째 Set 의 어떤 Elemenet 에 대응하는 관계를 의미한다.
Function
두 Set 을 X , Y 라는 기호로 지정하고 각각의 Set X ,Y 의 Element 를 x , y 라 할 때 X 에서 Y 로 대응되는 Function 을 y = f(x) 로 나타낸다.
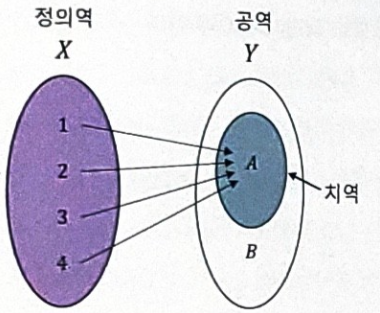
Domain , Codomain , Range
- Domain : Function 에서 왼쪽에서 위치한 첫 번째 Set
- Codomain : Function 에서 오른쪽에서 위치한 두 번째 Set
- Range : Domain 에 대응되는 Codomain 의 Element 만을 따로 모은 Subset
Function | 함수
Domain | 정의역
Codomain | 공역
Range | 치역
Subset | 부분집합
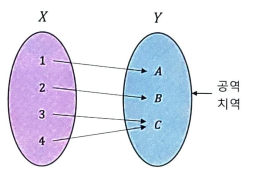
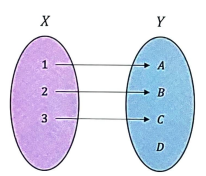
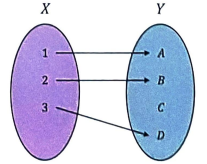
° Surjection
Codomain 의 모든 Element 가 Domain 에 대응되는 Function
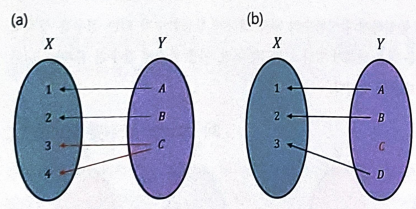
Surjection 의 예시
Surjection 가 아닌 예시
Surjection | 전사함수
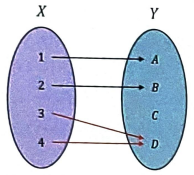
° Injection
Domain 과 Codomain 의 Element 가 1 : 1 로 대응되는 Function
Injection 의 예시
Injection 이 아닌 예시
Injection | 단사함수
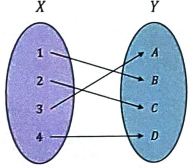
° Bijection
Domain 과 Codomain 의 모든 Element 가 빠짐없이 1:1 로 대응되는 Function
Bijection 의 예시
Bijection | 전단사함수
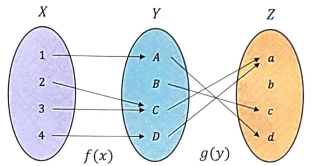
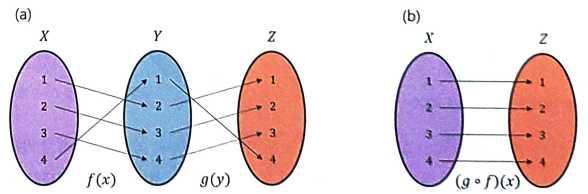
° Function Composition
2 개의 Function 을 연쇄적으로 이어 하나의 Function 으로 만드는 Operation
composite function 의 예시
두 함수 f(x) 와 g(y) 를 연쇄적으로 이어 마든 Composite function
위와 같은 Composite function 은 g(f(x)) 혹은 g ∘ f 로 표시한다.
Function Composition | 함수의 합성
Composite function | 합성 함수
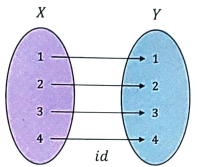
° Identity Function
Domain 과 Codomain 이 동일한 값으로 대응되는 Function
Identity function 의 예시
Identity 는 그림과 같이 어느 위치에 있든 Function Composition 의 결과가
동일한 대응 관계를 나타낸다.
Identity function | 항등 함수
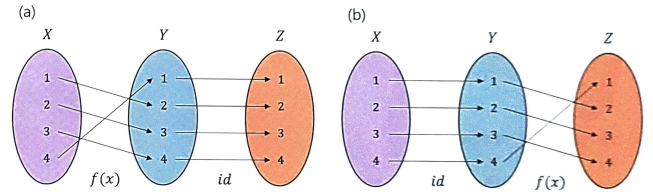
° Inverse Function
composite function 의 결과가 Identity function 이 되는 경우
Composition 의 결과가 Identity function 을 만들어내는 Function 을
Inverse Function 이라한다.
Inverse Function 의 도식화
Surjection 과 Injection 의 Inverse Function
모든 Function 이 Inverse Function 을 가지지는 못하며
특정 Function 이 Inverse Function 을 가지려면 반드시
Bijection 의 형태를 가져야 한다.
Cartesian Product
두 Set 의 Element 를 순서쌍으로 묶은 Element 의 Set 을 의미한다.