2025.4.18 알고리즘 코드카타

알고리즘 코드카타 - 124. 미로 탈출

문제 링크

문제 설명

1 x 1 크기의 칸들로 이루어진 직사각형 격자 형태의 미로에서 탈출하려고 합니다. 각 칸은 통로 또는 벽으로 구성되어 있으며, 벽으로 된 칸은 지나갈 수 없고 통로로 된 칸으로만 이동할 수 있습니다. 통로들 중 한 칸에는 미로를 빠져나가는 문이 있는데, 이 문은 레버를 당겨서만 열 수 있습니다. 레버 또한 통로들 중 한 칸에 있습니다. 따라서, 출발 지점에서 먼저 레버가 있는 칸으로 이동하여 레버를 당긴 후 미로를 빠져나가는 문이 있는 칸으로 이동하면 됩니다. 이때 아직 레버를 당기지 않았더라도 출구가 있는 칸을 지나갈 수 있습니다. 미로에서 한 칸을 이동하는데 1초가 걸린다고 할 때, 최대한 빠르게 미로를 빠져나가는데 걸리는 시간을 구하려 합니다.

미로를 나타낸 문자열 배열 maps가 매개변수로 주어질 때, 미로를 탈출하는데 필요한 최소 시간을 return 하는 solution 함수를 완성해주세요. 만약, 탈출할 수 없다면 -1을 return 해주세요.

---

제한 사항

• 5 ≤ maps의 길이 ≤ 100

• 5 ≤ maps[i]의 길이 ≤ 100

• maps[i]는 다음 5개의 문자들로만 이루어져 있습니다.

  S : 시작 지점
  E : 출구
  L : 레버
  O : 통로
  X : 벽

• 시작 지점과 출구, 레버는 항상 다른 곳에 존재하며 한 개씩만 존재합니다.

• 출구는 레버가 당겨지지 않아도 지나갈 수 있으며, 모든 통로, 출구, 레버, 시작점은 여러 번 지나갈 수 있습니다.

---

입출력 예

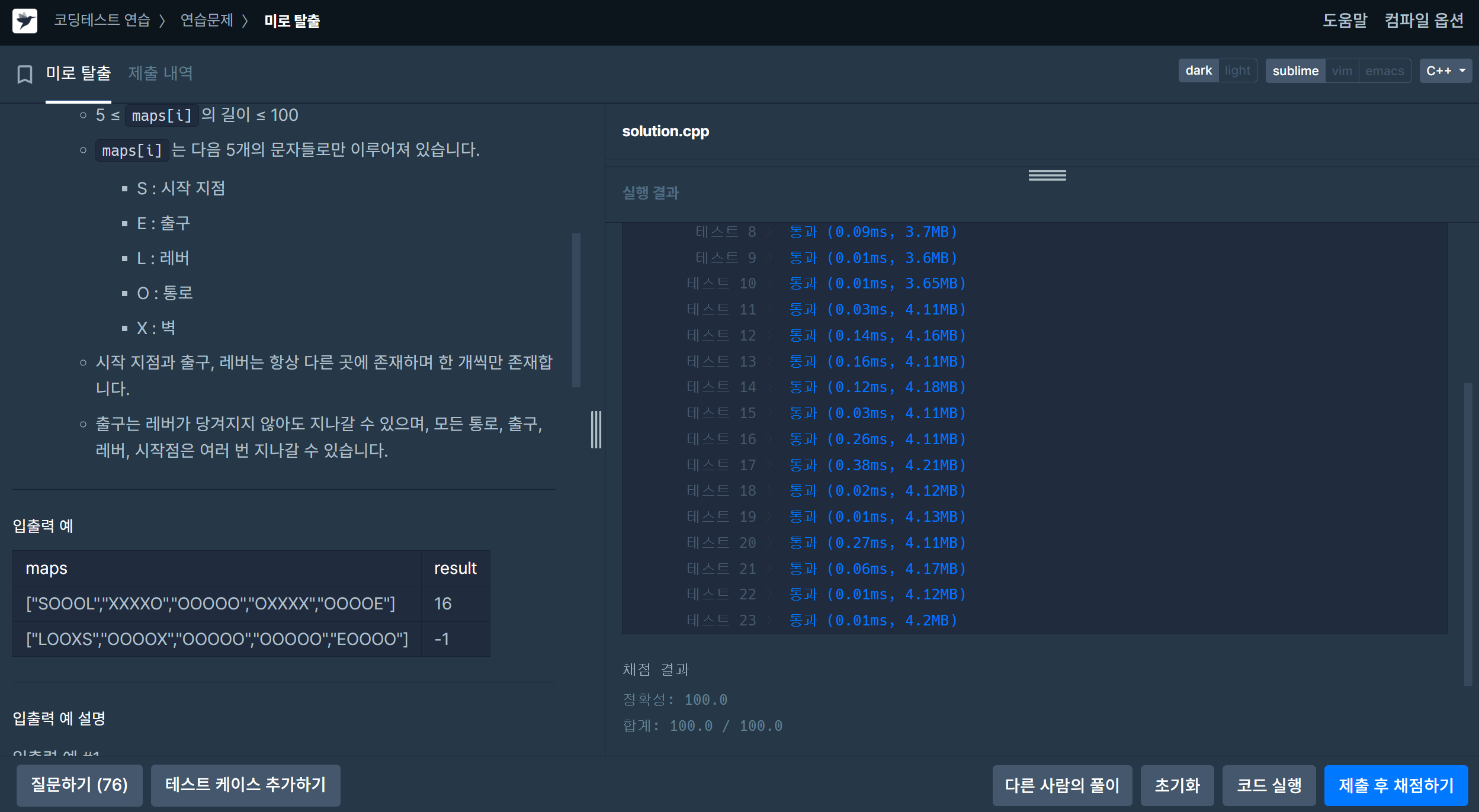
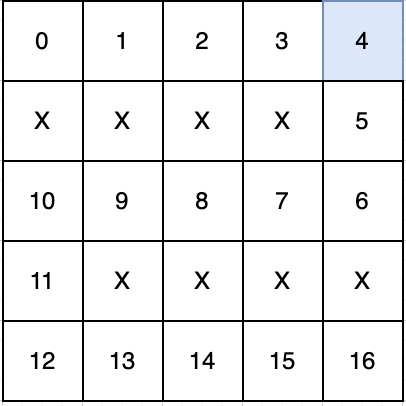
maps	result
["SOOOL","XXXXO","OOOOO","OXXXX","OOOOE"]	16
["LOOXS","OOOOX","OOOOO","OOOOO","EOOOO"]	-1

입출력 예 설명

입출력 예 #1

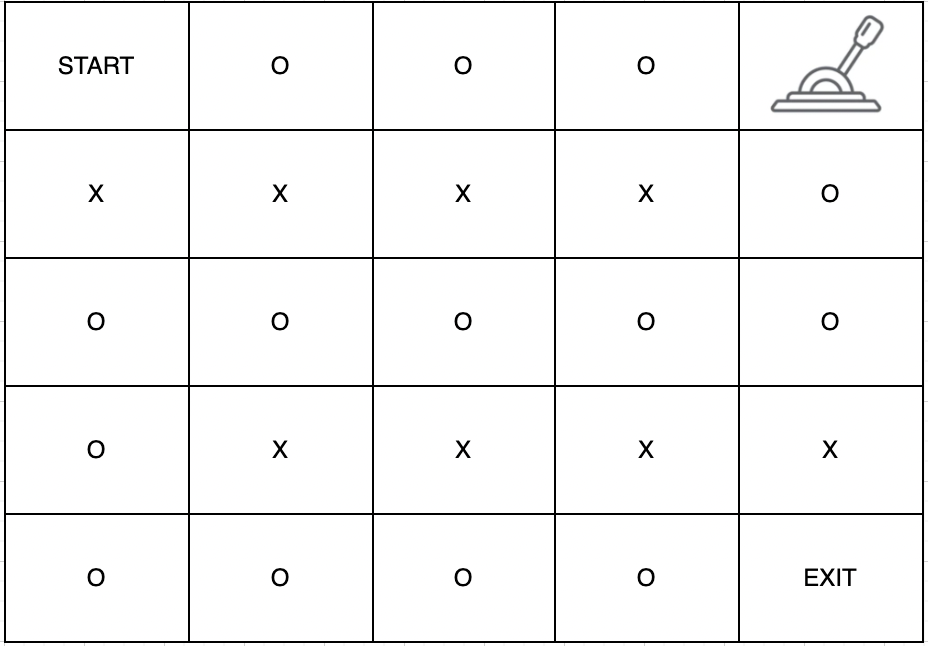
• 주어진 문자열은 다음과 같은 미로이며
  
  다음과 같이 이동하면 가장 빠른 시간에 탈출할 수 있습니다.
  
  4번 이동하여 레버를 당기고 출구까지 이동하면 총 16초의 시간이 걸립니다. 따라서 16을 반환합니다.

입출력 예 #2

• 주어진 문자열은 다음과 같은 미로입니다.
  
  시작 지점에서 이동할 수 있는 공간이 없어서 탈출할 수 없습니다. 따라서 -1을 반환합니다.

풀이 코드

#include <string>
#include <vector>
#include <queue>

using namespace std;

int pathfind(vector<string>& maps, char start, char goal)
{
    // 맵의 크기
    int rows = maps.size(), cols = maps[0].size();
    // start - goal 거리 저장할 벡터이면서 동시에 방문배열
    vector<vector<int>> dist(rows, vector<int>(cols, 0));
    
    // 4방향 이동
    int drow[] = {1, -1, 0, 0};
    int dcol[] = {0, 0, 1, -1};
    
    // 시작, 목표 좌표 {row, col}
    pair<int, int> posS = {0, 0}, posG = {0, 0};
    for(int i = 0; i < rows; i++)
    {
        for(int j = 0; j < cols; j++)
        {
            if(maps[i][j] == start) posS = {i, j};
            if(maps[i][j] == goal) posG = {i, j};
        }
    }
    
    queue<pair<int, int>> bfsq;
    bfsq.push(posS);
    dist[posS.first][posS.second] = 1;
    
    // 시작 - 레버 거리 구하기
    while(!bfsq.empty())
    {
        pair<int, int> current = bfsq.front();
        bfsq.pop();
        
        // 4방향 순회
        int row = current.first, col = current.second;
        for(int k = 0; k < 4; k++)
        {
            int newrow = row + drow[k];
            int newcol = col + dcol[k];
            
            if(newrow >= rows || newrow < 0 || newcol >= cols || newcol < 0) continue;
            if(maps[newrow][newcol] == 'X') continue;
            if(dist[newrow][newcol] != 0) continue;
            
            dist[newrow][newcol] = dist[row][col] + 1;
            if(maps[newrow][newcol] == goal) return dist[newrow][newcol] -1; 
            bfsq.push({newrow, newcol});
            
        }
    }
    return -1;
}

int solution(vector<string> maps) {
    int answer = 0;
    int SL = pathfind(maps, 'S', 'L');
    int LE = pathfind(maps, 'L', 'E');
    if(SL == -1 || LE == -1) return -1;
    return SL + LE;
}

• 최단 거리, 격자 를 보고 떠올라야 하는 것은? BFS

• 118. 거리두기 확인하기, 111. 무인도 여행과 비슷한 BFS 유형의 문제.

• 차이점이라면 무인도 여행에서는 BFS로 방문하는 모든 칸의 수 확인이었고, 거리두기 확인하기에서는 BFS로 시작지점 2레벨 이하 확인이었다는 것.

• 이 문제는 시작지점에서의 최단거리를 구하는 문제이다. 시작-레버 최단거리, 레버-출구 최단거리를 구해 더하는 문제.

• 최단거리 문제에서 격자형 그래프를 그리는 경우 방문 배열+거리(레벨) 기록 역할을 하는 배열이 있으면 편한가?

이전에 풀었던 문제를 참고해서 푸니 생각보다 스무스하게 풀려서 기분이 좋다. 점차 숙달되는 느낌이 드는데 다른 유형도 풀어볼 수 있으면 좋겠다.