2025.4.2 알고리즘 코드카타

알고리즘 코드카타 - 109. 연속된 부분 수열의 합

문제 링크
풀이 참고 - 투 포인터 알고리즘 : https://youtu.be/iSjvuixMPmQ?si=pw5PJzmdKqc6Kvzo

문제 설명

비내림차순으로 정렬된 수열이 주어질 때, 다음 조건을 만족하는 부분 수열을 찾으려고 합니다.

• 기존 수열에서 임의의 두 인덱스의 원소와 그 사이의 원소를 모두 포함하는 부분 수열이어야 합니다.
• 부분 수열의 합은 k입니다.
• 합이 k인 부분 수열이 여러 개인 경우 길이가 짧은 수열을 찾습니다.
• 길이가 짧은 수열이 여러 개인 경우 앞쪽(시작 인덱스가 작은)에 나오는 수열을 찾습니다.

수열을 나타내는 정수 배열 sequence와 부분 수열의 합을 나타내는 정수 k가 매개변수로 주어질 때, 위 조건을 만족하는 부분 수열의 시작 인덱스와 마지막 인덱스를 배열에 담아 return 하는 solution 함수를 완성해주세요. 이때 수열의 인덱스는 0부터 시작합니다.

---

제한사항

• 5 ≤ sequence의 길이 ≤ 1,000,000
• 1 ≤ sequence의 원소 ≤ 1,000
• sequence는 비내림차순으로 정렬되어 있습니다.
• 5 ≤ k ≤ 1,000,000,000
• k는 항상 sequence의 부분 수열로 만들 수 있는 값입니다.

입출력 예

sequence	k	result
[1, 2, 3, 4, 5]	7	[2, 3]
[1, 1, 1, 2, 3, 4, 5]	5	[6, 6]
[2, 2, 2, 2, 2]	6	[0, 2]

입출력 예 설명
입출력 예 #1
[1, 2, 3, 4, 5]에서 합이 7인 연속된 부분 수열은 [3, 4]뿐이므로 해당 수열의 시작 인덱스인 2와 마지막 인덱스 3을 배열에 담아 [2, 3]을 반환합니다.

입출력 예 #2
[1, 1, 1, 2, 3, 4, 5]에서 합이 5인 연속된 부분 수열은 [1, 1, 1, 2], [2, 3], [5]가 있습니다. 이 중 [5]의 길이가 제일 짧으므로 해당 수열의 시작 인덱스와 마지막 인덱스를 담은 [6, 6]을 반환합니다.

입출력 예 #3
[2, 2, 2, 2, 2]에서 합이 6인 연속된 부분 수열은 [2, 2, 2]로 3가지 경우가 있는데, 길이가 짧은 수열이 여러 개인 경우 앞쪽에 나온 수열을 찾으므로 [0, 2]를 반환합니다.

---

풀이 코드

#include <string>
#include <vector>
#include <algorithm>
using namespace std;

// 정답 후보 비교 함수
// 시작점 끝점의 거리 비교 -> 거리가 같으면 시작점 비교
bool compare(pair<int, vector<int>>& a, pair<int, vector<int>>& b)
{
    if(a.first == b.first)
    {
        return a.second[0] < b.second[0]; 
    }
    return a.first < b.first;
}

vector<int> solution(vector<int> sequence, int k) {
    vector<int> answer;
    int L = 0, R = 0;	// 두 개의 포인터 선언
    int sum = 0;		// 두 포인터 사이(부분 수열)의 합
    
    // 조건이 맞을 때 <두 포인터 거리, {시작점, 끝점}> 저장
    pair<int, vector<int>> dist;
    // 정답 후보들을 저장할 배열
    vector<pair<int, vector<int>>> startend;
    
    // 두 번째 포인터가 마지막 인덱스가 될 때까지 진행
    while(R < sequence.size())
    {
        // 합에 끝점의 값 더하기
        sum += sequence[R];
        
        // 부분 수열의 합이 k보다 작고 시작점이 끝점보다 앞일 때
        while(sum > k && L <= R)
        {
            // 부분 수열의 합에서 시작점 제외
            // 시작점 증가
            sum -= sequence[L];
            L++;
        }
        // 조건이 맞으면 정답 후보에 추가
        if(sum == k)
        {
            startend.push_back(make_pair(R-L + 1, vector<int>{L,R}));
        }
        
        // 조건에 안맞으면 끝점 증가
        R++;
    }
    // 정답 후보 정렬후 첫 번째 정답 후보를 answer에 추가
    sort(startend.begin(), startend.end(), compare);
    answer.push_back(startend[0].second[0]);
    answer.push_back(startend[0].second[1]);
    return answer;
}

---

풀이 과정

• 투 포인터 알고리즘 를 이용해서 풀 수 있는 문제

• 두 개의 포인터를 만들어서 주어진 배열 sequence를 순회한다. 이 때 어떤 조건일 때 시작 포인터와 끝 포인터를 증가시키는가를 설정하는 것이 풀이의 핵심

  포인터의 진행 예시

  1. 두 포인터가 같은 방향으로 진행하는 것
  2. 양 끝에서 시작해 서로 가까워지는 것
  3. 하나는 한 쪽 방향으로만 진행하고, 상황에 따라 다른 하나는 양쪽으로 이동하는 것

• 문제에서 먼저 요구하는 것은 `sequence의 부분 수열의 합이 k가 되는 것`이다.

• 또한 부분수열의 크기가 가장 작은 것을 정답으로 요구하고 있기 때문에, 1. 두 포인터가 같은 방향으로 진행하는 것을 선택하여 한 칸씩 늘려가며 조건을 비교한다.

---

위 사항에 유의하며 문제를 풀어보면 흐름은 아래와 같다.
sequence = {1, 2, 3, 4, 5} , k = 7 일 때

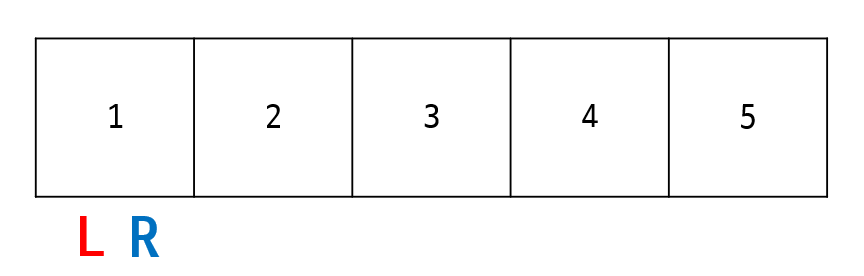
1. 초기화 단계 직후 포인터 L,R의 위치, 루프에 막 진입한 상태

while(R < sequence.size())
{
    sum += sequence[R];
        
    /*while(sum > k && L <= R)
    {
        sum -= sequence[L];
        L++;
    }
    if(sum == k)
    {
        startend.push_back(make_pair(R-L + 1, vector<int>{L,R}));
    }
    */
    R++;
}

2. sum > k와 sum == k 를 만족하지 않으므로 주석처리 되지 않은 부분만 실행, sum = 1, R = 1이 된다. 그리고 while문 재진입.

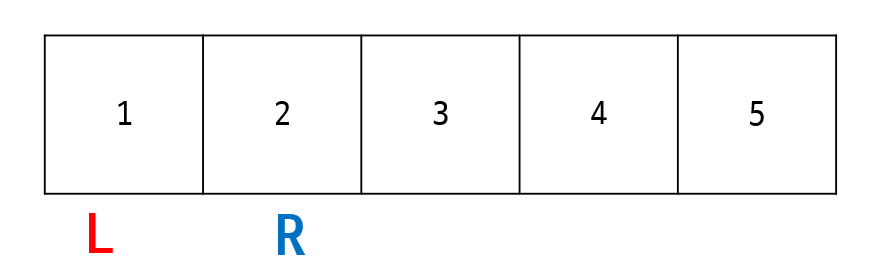
3.↑2번째 루프에 진입한 상태.
여전히 조건을 만족하지 않으므로 2번과 동일한 프로세스 실행.
sum = 3, R = 2가 된다.

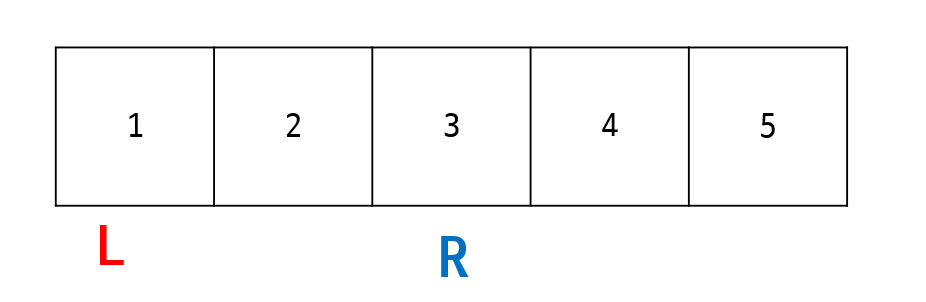
↑ 2번째 루프 종료 전

while(R < sequence.size())
{
    sum += sequence[R];
        
    /*while(sum > k && L <= R)
    {
        sum -= sequence[L];
        L++;
    }
    if(sum == k)
    {
        startend.push_back(make_pair(R-L + 1, vector<int>{L,R}));
    }
    */
    R++;
}

4. 3번째 루프 진입. sum = 6, R = 3. 다음 단계에서 sum > k를 만족할 것 같다.

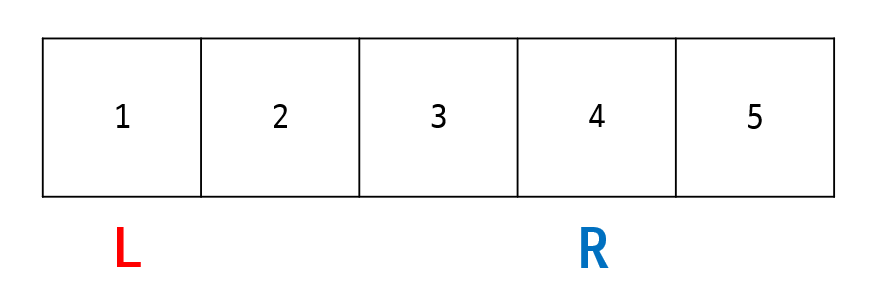
↑ 3번째 루프 종료 전

5. 4번째 루프 시작.

while(R < sequence.size())
{
    sum += sequence[R];
        
    while(sum > k && L <= R)
    {
        sum -= sequence[L];
        L++;
    }
    /*if(sum == k)
    {
        startend.push_back(make_pair(R-L + 1, vector<int>{L,R}));
    }
    */
    R++;
}

5. sum = 10이 되고, 내부 while문 진입 조건을 만족하여
   L = 1, sum = 9 된다.
   
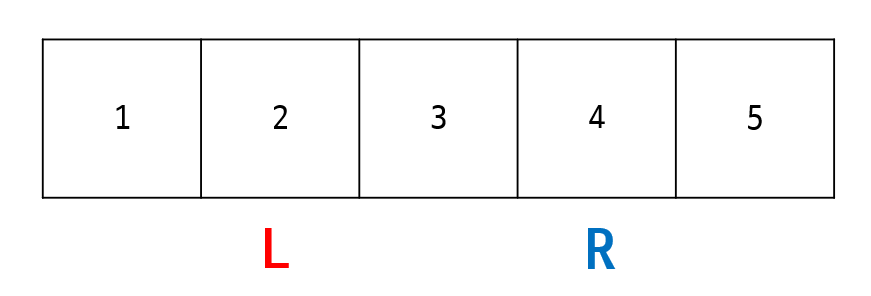
6. 그러나 여전히 sum > k && L <= R 를 만족하므로 내부 while문 재진입.
   L=2, sum = 7이 된다.
   
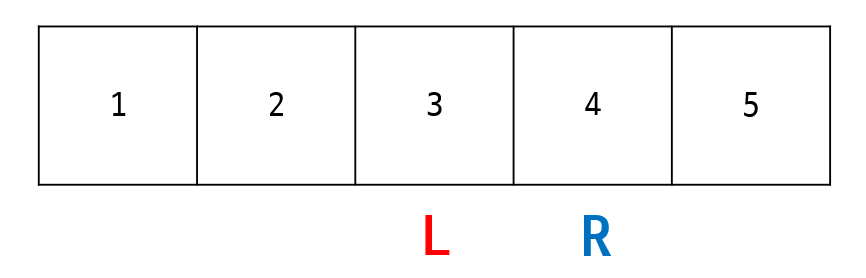
   그리고 sum > k 를 만족하지 못하므로 while문에서 빠져나와
   if(sum == k)에 진입.
   정답후보 배열에 R - L + 1 = 2 {L, R} = {2, 3} 을 추가.
   그리고 다시 R++; 후 while문 종료.
   이 시점에서 문제가 원하는 정답은 구해졌으므로 이후의 계산 과정은 생략하겠음.