벌써 코테 스터디를 시작한고 4주가 지났습니다.
비록 많이 풀지도 않고, 매번 정답을 맞는건 아니지만 꾸준히 하다보니공부가 되는거 같긴해요.
코테 공부를 하면서 항상 느끼는건 어떤 문제를 봤을때, 어떤 자료구조가 적합할지, 어떤 알고리즘을 선택해야 할 지 생각하는 좋은 습관이 생긴거 같아요. 물론 아직 알고리즘은 항상 틀리고,,,, 아직 잘 모르지만 한 단계씩 상승하는 느낌을 받습니다.
그렇다면 이번주엔 어떤걸 공부했는지 보러 가시죠!
힙(Heap)
- 힙은 완전 이진트리(Complete Binary Tree) 구조를 가진 자료구조 입니다.
- 각 노드의 값이 특정한 순서를 따르는 특성을 가집니다.
- 그렇기 때문에 힙은 주로 우선순위 큐(Priority Queue)를 구현하는 데 사용됩니다.
- 힙은 두 가지 유형으로 나뉩니다.
최소 힙 (Min-Heap)
- 모든 부모 노드의 값이 자식 노드의 값보다 작거나 같은 구조입니다.
- 루트 노드(root)는 힙에서 가장 작은 값을 가집니다.
- 최소 힙에서는 가장 작은 값을 빠르게 찾을 수 있으며, 이것이 우선순위 큐에서 최소값을 우선적으로 처리하는 데 유용합니다.
최대 힙 (Max-Heap)
- 모든 부모 노드의 값이 자식 노드의 값보다 크거나 같은 구조입니다.
- 루트 노드(root)는 힙에서 가장 큰 값을 가집니다.
- 최대 힙에서는 가장 큰 값을 빠르게 찾을 수 있습니다.
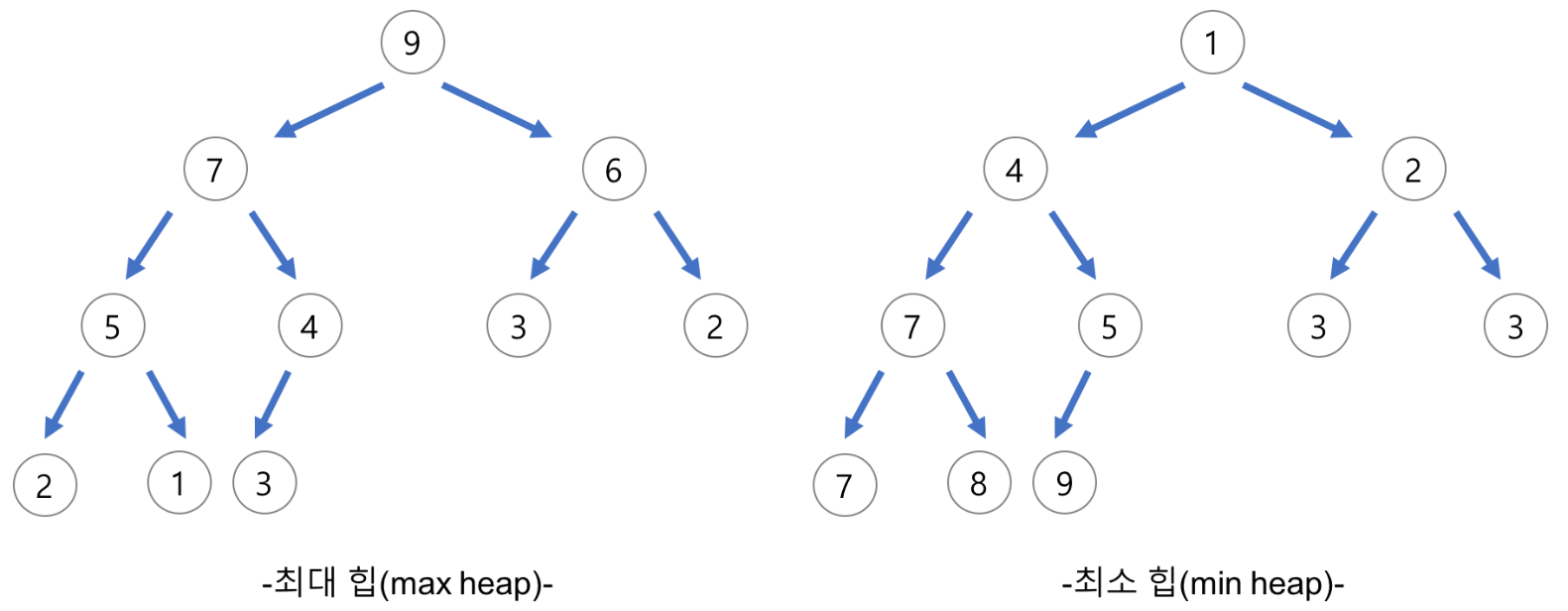
- 파이썬의 heapq 모듈은 기본적으로 최소 힙(Min-Heap)을 제공합니다.
level1. 명예의 전당
import heapq
def solution(k, score):
ranking = []
result = []
for i in score:
# 명예의 전당의 크기 조건
if len(ranking) < k:
# 힙푸쉬를 이용하여 heap에 score 담기
heapq.heappush(ranking, i)
else:
# 힙푸쉬팝을 이용하여 랭킹의 점수를 추가하며, 최하점은 pop!
if i > ranking[0]:
heapq.heappushpop(ranking, i)
# 매일 ranking 최하위 점수를 result에 추가
result.append(ranking[0])
return result-
이 코드의 포인트는 매일 상위 k명의 점수를 추적하여, k명 중 가장 낮은 점수를 기록하는 것입니다.
-
문제를 보고 heap 자료구조를 사용한 이유는 2가지가 있습니다.
최소 힙을 이용: 이 문제에서는 상위 k명 중 가장 낮은 점수를 지속적으로 기록해야 하므로 루트에 가장 작은 값을 유지시키는 최소 힙의 기능이 필요했습니다.
heapq.heappushpop()이용: 새로운 점수를 추가하고, 기존의 최솟값을 한 번의 연산으로 대체할 수 있어 시간 복잡도가O(logk)로 유지됩니다.
정렬(sort)
- 정렬은 데이터 구조(리스트, 튜플, 문자열 등)를 특정 기준에 따라 순서대로 배열하는 과정을 의미합니다.
- 정렬은 주로 오름차순(작은 값부터 큰 값)이나 내림차순(큰 값부터 작은 값)으로 이루어집니다.
- 랭킹을 구해야 하거나, 최솟값/최댓값/중간값 등을 구할때 유용하게 쓰이는 함수죠.
level0. 진료 순서 정하기
def solution(emergency):
answer = []
sort_numbers = sorted(emergency, reverse=True)
for i in emergency:
answer.append(sort_numbers.index(i)+1)
return answer- 이 문제의 포인트는 리스트 emergency의 요소들이 각자 몇 번째로 큰 숫자인지 순위를 매겨 새로운 리스트 answer에 그 순위를 저장하는 것입니다.
아래는 이 문제의 풀이 단계입니다.
- 리스트 복사 및 내림차순 정렬
sort_numbers = sorted(emergency, reverse=True) - 순위 계산
for i in emergency: answer.append(sort_numbers.index(i) + 1)
아주 간단하죠?
물론 레벨0의 문제이기 때문이지만, 정렬과 인덱스를 잘 이해하는 것이 다른 문제들에서도 중요할 것으로 보여집니다.
마무리
앞으로는 알고리즘과 같은 조금 더 복잡한 형식의 문제를 보여드릴텐데 글의 길이를 감안하여 따로 지식 공유 글을 작성할 수도 있을거 같습니다.
긴 글 읽어주셔서 감사합니다.

