선형회귀(linear regression)

1.선형회귀분석(linear regression)이란?

• 과거 부터 지금까지 널리 사용이 되어지고 있으며, 독립변수(x)와 종속변수(y)의 관계를 선의 형태로 모델링하여 다른 입력값을 넣었을 때 발생할 출력값을 예측하는 머신러닝 방법이다.
  
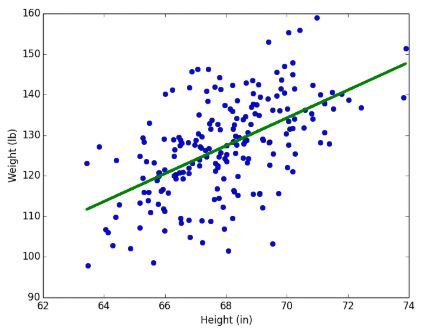
  위의 그래프를 보면 키와 몸무게에 대한 데이터를 펼쳐놓은 걸 볼 수 있는데, 저 데이터들 위에 그려진 저 선으로 우리는 예측을 할 수 있게 되는 것이다.
  이 그래프에서는 키가 바로 독립변수(x)이고 몸무게가 종속변수(y)에 해당하게 된다. 비록 이 그래프에서는 정확하게 데이터가 선위에 딱 맞아 떨어지지는 않지만, 저 선은 일차방정식 y = wx + b로 나타 낼 수가 있다. 선의 모양은 w와 b에 의해 달라지므로 우리가 이 선형회귀분석을 하는 목적은 우리의 데이터가 가장 잘 들어 맞을 수 있는 w,b값을 찾는 과정이라고 보면된다.

• 선형회귀분석에는 단순 선형 회귀 분석과 다중 선형 회귀 분석이 있다.
  1. 단순 선형 회귀 분석(Simple Linear Regression Analysis)
  
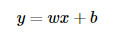
  위의 그래프 에서 보았던거 처럼 단순히 종속변수 1개, 독립변수 1개로 이루어진 형태이다. 여기서 w는 가중치(weight)이라고 하고 별도로 더해지는 값인 b를 편향치(bias)라고 한다.

  2. 다중 선형 회귀 분석(Multiple Linear Regression Analysis)
     
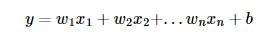
     위 그래프처럼 단순히 키와, 몸무게 만이 아닌 예를들면 집값을 예로들수가 있다. 집의 크기에 뿐만이 아니라, 역세권이냐, 학교가 근처에 있냐, 방의 갯수 등 다양한 요소가 집의 가격에 영향을 줄 수 있기 때문이다. 종속변수의 값은 1개이지만 독립변수의 수가 여러개를 가진 형태를 가진다.

2. 가설(Hypothesis) 세우기

머신러닝에서는 x와 y의 관계를 유추하기 위해서 수학적으로 식을 세우게 되는데 이를 가설(Hypothesis)라고 한다.

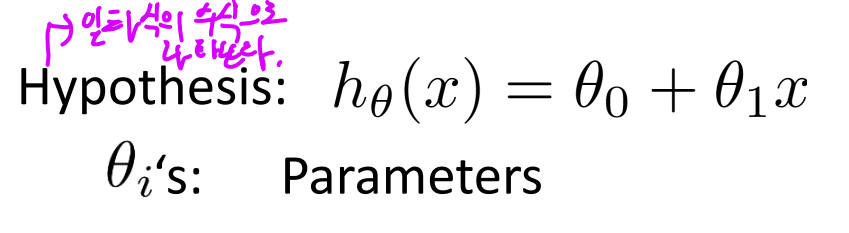
3. 비용 함수(Cost function)

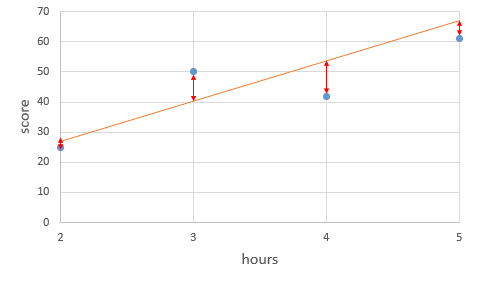
가설을 세운 후에 그 식을 바탕으로 임의의 직선을 그어보면 우리의 데이터와는 어느정도의 차이를 보이는 것을 볼 수가 있다. 그 차이를 오차라고 하며, 이때 실제값과 예측값에 대한 오차에 대한 식을 비용 함수(Cost Function) 이라고 한다.

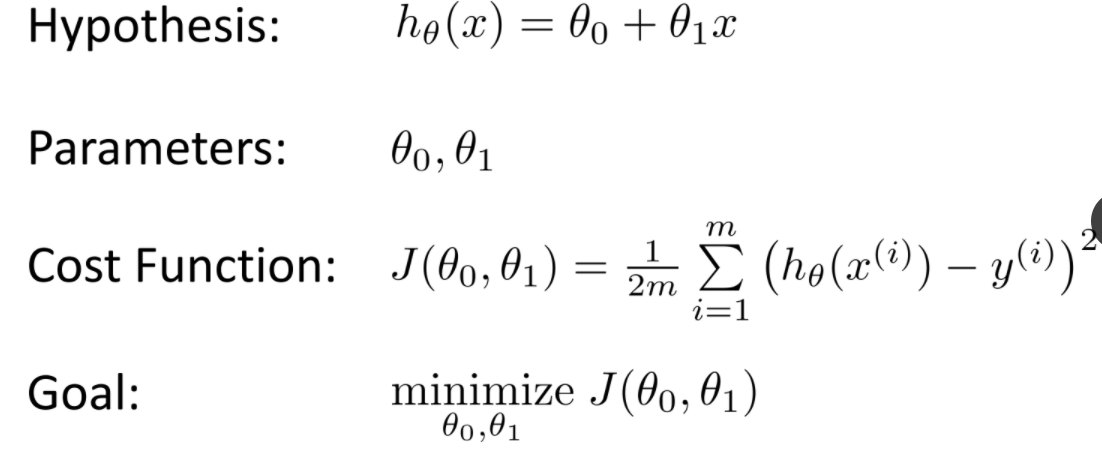
오차의 크기를 측정하기 위한 가장 기본적인 방법으로는 각 오차를 모두 더하는 방법이 있는데, 이 오차는 음수, 양수 모두 존재 할 수가 있기 때문에 오차크기의 절대적 크기를 구하기 위해서 제곱을 하여 더해준다. 그러고 데이터의 개수로 나누어 주게 되면, 평균 제곱 오차(Mean squered Error, MSE)를 구할 수가 있다. 오차가 작아질수록 MSE는 작아 지므로 Cost function을 최소가 되게 하는 parameters를 구하면 예측값의 정확도가 올라가게 된다.

4. 경사하강법(Gradient Descent)

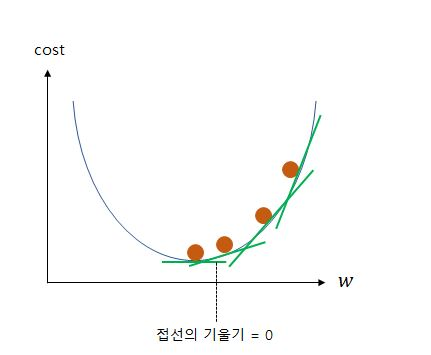
적절한 w와 b를 찾아내는 과정을 머신러닝에서는 학습(training)이라고 하는데, 선형회귀분석에서는 Gradient Descent 알고리즘을 이용하여 최적의 값을 구한다.

cost가 최소화가 되는 점은 접선의 기울기가 0이 되는 지점으로 cost function의 미분값이 0이 되는걸 의미한다. 그래서 w의 값을 계속 0과 가까워지게 업데이트를 하는 과정을 반복하게 된다.

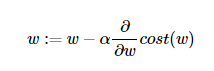
이를 식으로 나타내면 위와 같은 식으로 나타낼 수 있는데, 현재 w에서의 접선의 기울기와 α의 곱한 값을 현재 w에서 빼서 새로운 의 값으로 한다는 것을 의미한다.

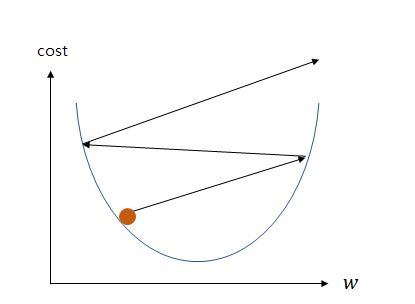
α는 학습률(learning rate)를 말하며 w의 값을 변경할 때, 얼마나 크게 변경할지를 결정하며 0과 1사이의 값을 가지도록 설정해준다. α값을 너무 크게 설정하면 위 그래프 처럼 w의 값이 발산하는 상황을 보여주며 α값을 너무 작게 설정해버리면 최적의 값으로 수렴할 때 까지의 시간이 오래걸리게 된다.

참고자료

1.<딥 러닝을 이용한 자연어 처리 입문> https://wikidocs.net/21670
2.https://hleecaster.com/ml-linear-regression-concept/