정렬
데이터를 특정한 기준에 따라서 순서대로 나열하는 것
버블정렬
서로 인접한 두 원소의 크기를 비교한 후, 정렬한다.
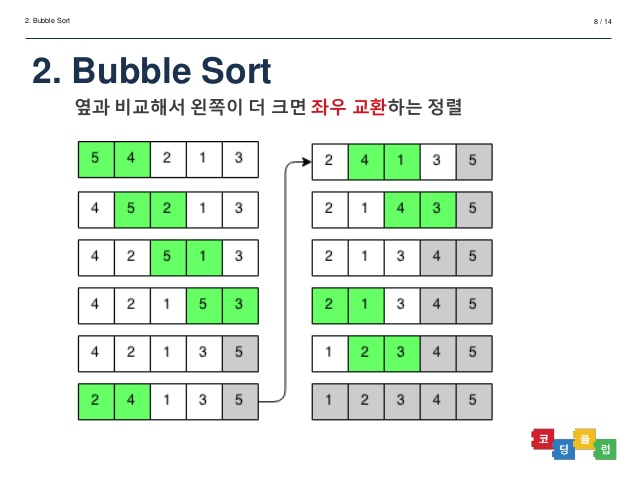
어쨌든 제일 큰 놈은 뒤로 보내버림
선택정렬
데이터가 무작위로 여러 개 있을 때, 이 중에서 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸고, 그 다음 작은 데이터를 선택해 앞에서 두번째 데이터와 바꾸는 과정을 반복하는 것
=>가장 작은 것을 선택한다
시간 복잡도
N+(N-1)+(N-2)+....1 = (N^2+N)/2
따라서 O(N^2)
=> 이미 정렬이 되어있더라도 순환하며 가장 작은 것을 찾아내야하기 때문에, 어떤 상황에서라도 n^2의 시간복잡도를 가진다.
선택 정렬이 버블정렬 보다는 빠름
선택정렬 -> 반복 마다 최소값을 찾는 과정에서 비교 회수가 점차 줄어든다.
삽입정렬
그 앞까지의 데이터는 이미 정렬되어있다고 가정, 다음에 오는 원소와 앞까지의 데이터의 대소를 비교함으로써 특정원소의 좌,우에 삽입
array = [7,6,5,9,0,3,1,4,8]
for i in range(1,len(array)):
for j in range(i,0,-1):
if array[j]<array[j-1]:
array[j],array[j-1] = array[j-1],array[j]
else:
break
print(array)삽입 정렬의 시간복잡도
이중 반복문을 쓰기 때문에 O(N^2)이나, 최선의 경우(리스트가 정렬된 상태) O(N)의 시간복잡도를 가진다.
퀵 정렬
기준 데이터(피벗)를 설정하고, 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾼다.
array=[5,7,8,0,3,1,6,2,4,8]
def quick_sort(array, start, end) :
if start >= end: #원소가 1개인 경우 종료
return
pivot = start
left = start + 1
right = end
while left <= right:
#피벗보다 큰 데이터를 찾을 때까지 반복
while left <= end and array[left] <= array[pivot]:
left += 1
#피벗보다 작은 데이터를 찾을 때까지 반복
while right > start and array[right] >= array[pivot]:
right -= 1
if left > right: #엇갈렸다면 작은 데이터와 피벗을 교체
array[right], array[pivot] = array[pivot], array[right]
else: # 엇갈리지 않았다면 작은 데이터와 피벗을 교체
array[left], array[right] = array[right], array[left]
#분할 이후 왼쪽과 오른쪽 부분에서 각각 정렬 수행
quick_sort(array, start, right - 1)
quick_sort(array, right +1, end)
quick_sort(array, 0, len(array)-1)
print(array)아래는 파이썬의 장점을 살린 코드이나, 동작이 조금 더 느리다.
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array):
# 리스트가 하나 이하의 원소만을 담고 있다면 종료
if len(array) <= 1:
return array
pivot = array[0] #피벗은 첫 번째 원소
tail = array[1:] # 피벗을 제외한 리스트
left_side = [x for x in tail if x <= pivot] #분할된 왼쪽 부분
right_side = [x for x in tail if x >= pivot] #분할된 오른쪽 부분
#분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체 리스트를 반환
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
print(quick_sort(array))퀵 정렬의 시간복잡도
O(NlogN)
벗값의 위치가 변경되어 분할이 일어날 때마다 정확히 왼쪽 리스트와 오른쪽 리스트를 절반씩 분할한다면 데이터의 개수가 n개라면 높이는 logN이 된다.
계수 정렬
특정한 조건이 부합할 때만 사용할 수 있지만 배우 빠른 정렬 알고리즘
데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때에만 사용할 수 있다.
(주어진 배열과 같은 크기의 배열을 하나 더 만들기 때문에 공간 복잡도가 증가함)
array = [7,5,9,0,3,1,6,2,9,1,4,8,0,5,2]
#모든 범위를 포함하는 리스트 선언(모든 값은 0으로 초기화)
print(max(array))
count = [0] * (max(array) + 1)
for i in range(len(array)) :
count[array[i]] += 1 # 각 데이터에 해당하는 인덱스의 값 증가
for i in range(len(count)): # 리스트에 기록된 정렬 정보 확인
for j in range(count[i]):
print(i, end =' ') # 띄어쓰기를 구분으로 등장한 횟수만큼 인덱스 출력계수 정렬의 시간 복잡도
데이터의 개수가 N, 데이터 중 최대값의 크기를 K라고 할 때, O(N+K)
