B tree

개념과 특징

B tree는 DB인덱스와 관련있는 자료구조이다.
B tree는 BST(이진 탐색 트리)를 일반화한 구조이다.
B tree의 부모 노드는 자녀 노드를 두 개 이상 가질 수 있다.
B tree의 노드가 자녀 x개를 가졌다면 key의 개수는 x-1개이다.
B tree 노드 내 key들은 오름차순으로 저장된다.
B tree 모든 leaf 노드들은 같은 레벨에 있다.

이진 탐색 트리

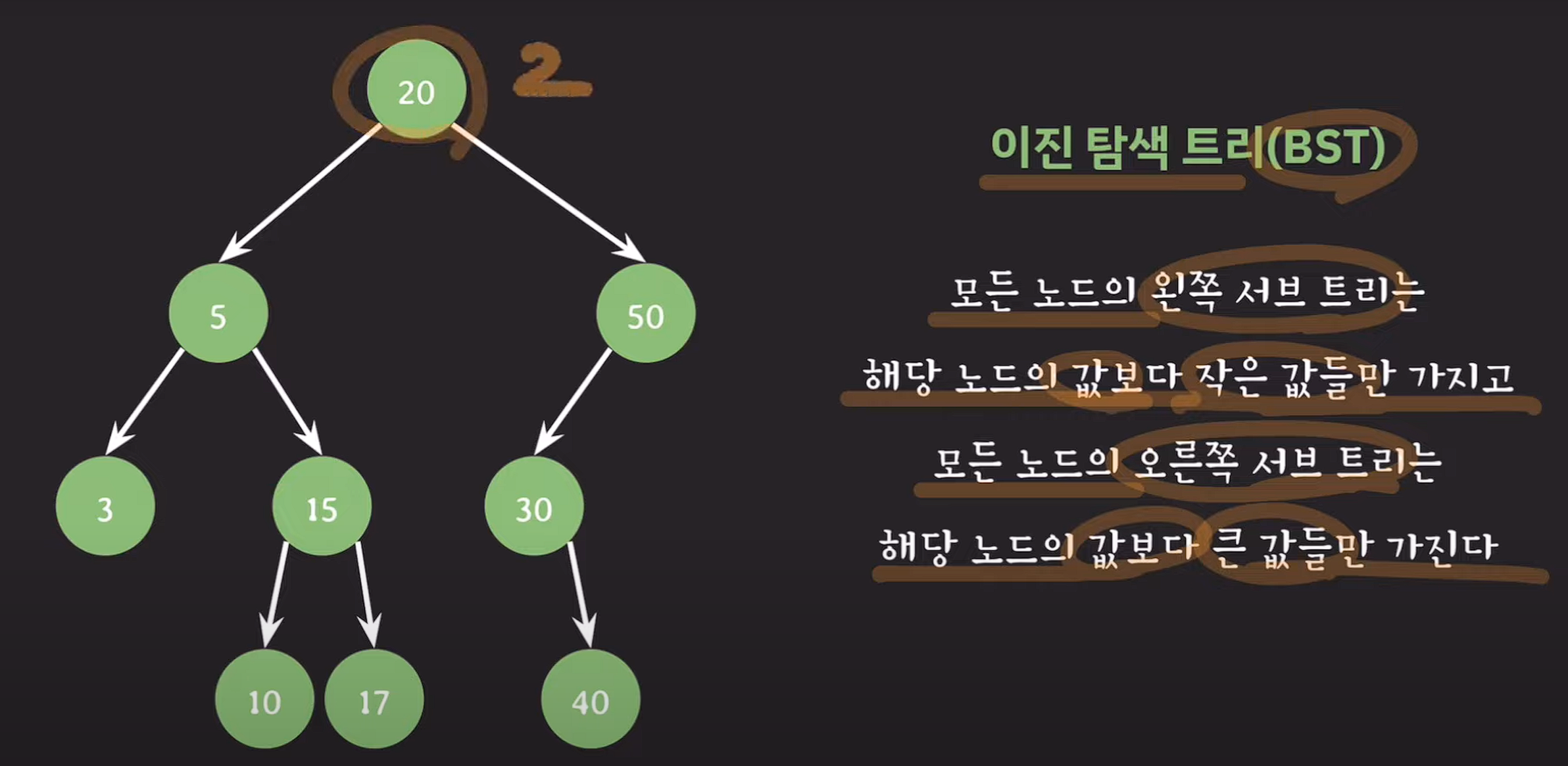
자녀 노드는 최대 두 개 까지 가질 수 있다.

만약 자녀 노드를 3개 가지고 싶다면 어떻게 할까?

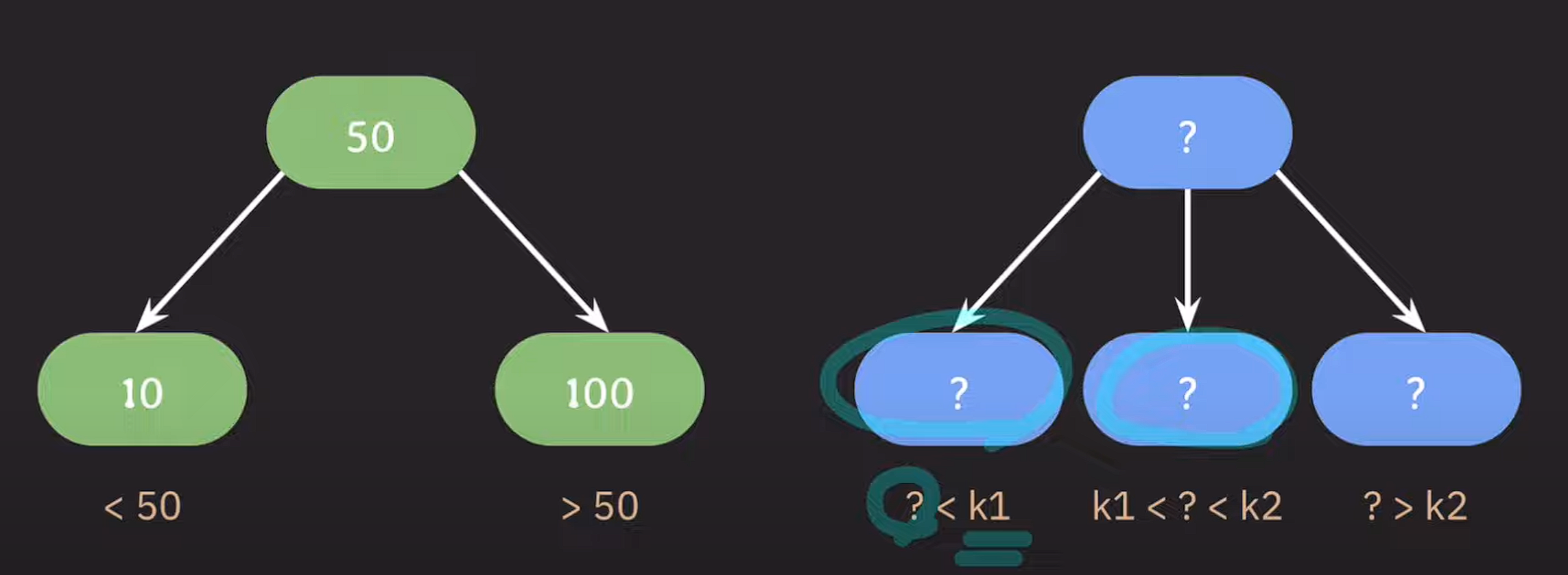
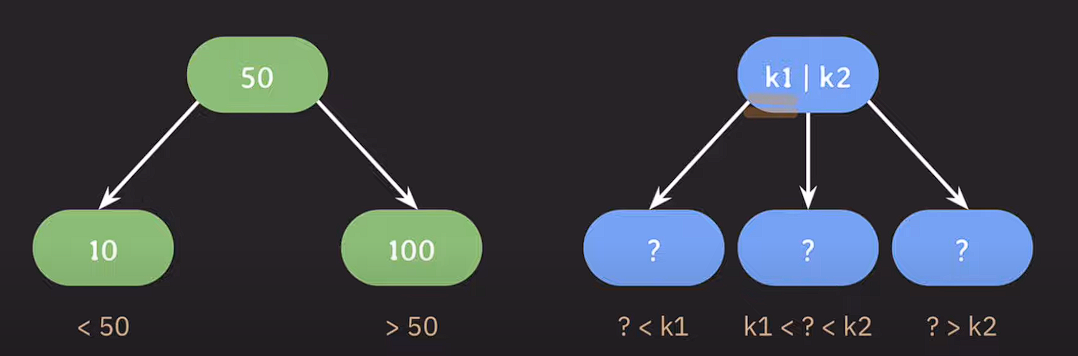
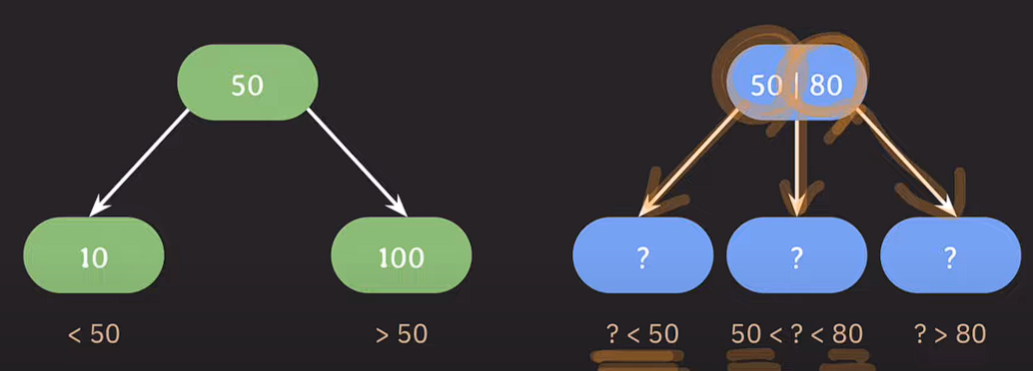
부모노드의 왼쪽 서브트리는 부모의 값보다 작고, 오른쪽 서브트리는 부모의 값보다 크다. 자녀노드를 3개가지고 싶은 경우 값1개로 범위를 지정할 수 없기 때문에, 부모노드에 값을 2개 저장한다.

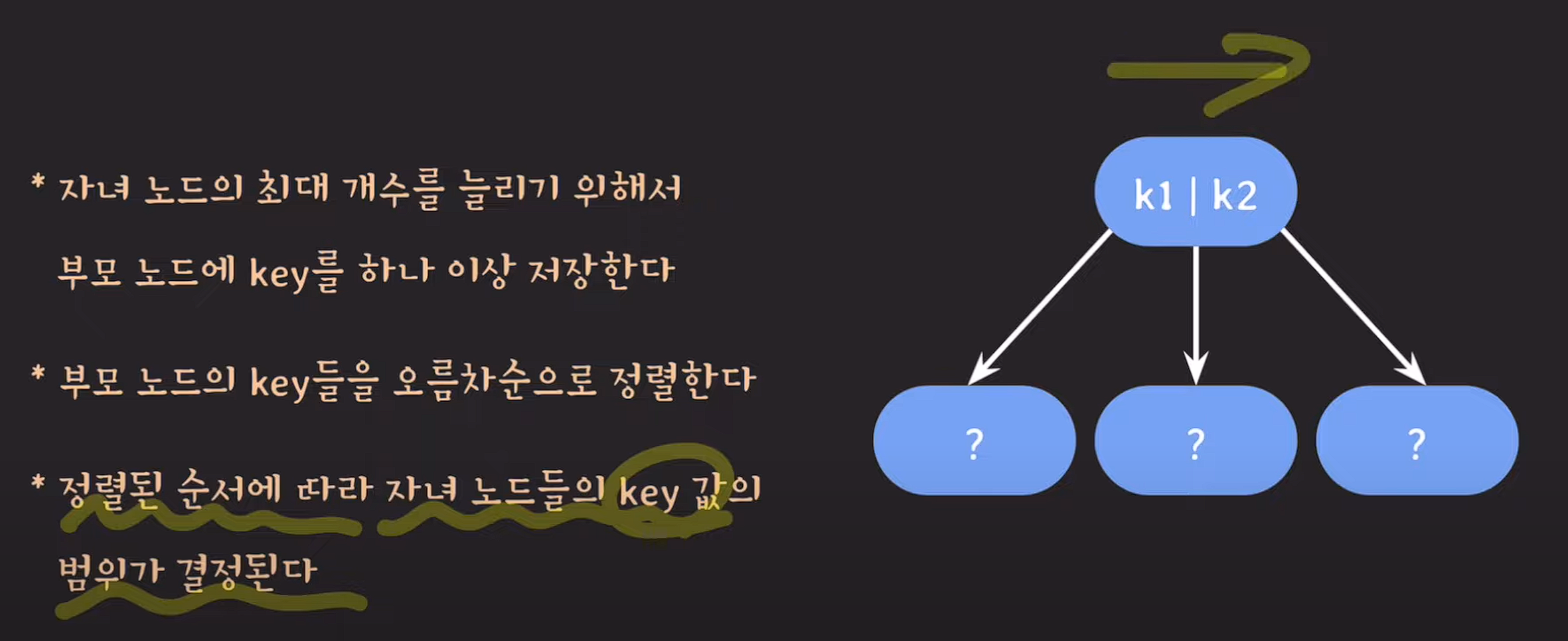
B tree 개념

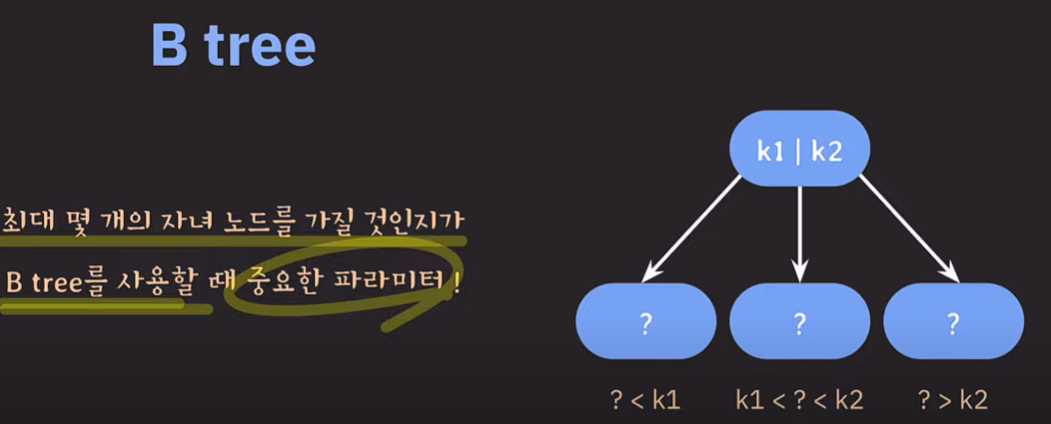
이진 탐색 트리와 비슷하지만, 자녀 노드의 최대 개수를 입맛에 맞게 결정해서 쓸 수 있다. 자녀 노드가 더 필요한 경우 부모 노드의 데이터 갯수를 추가하여 오름차순 정렬 후 범위에 맞게 자녀 노드들을 구성할 수 있다.

M

각 노드의 최대 자녀 노드 수

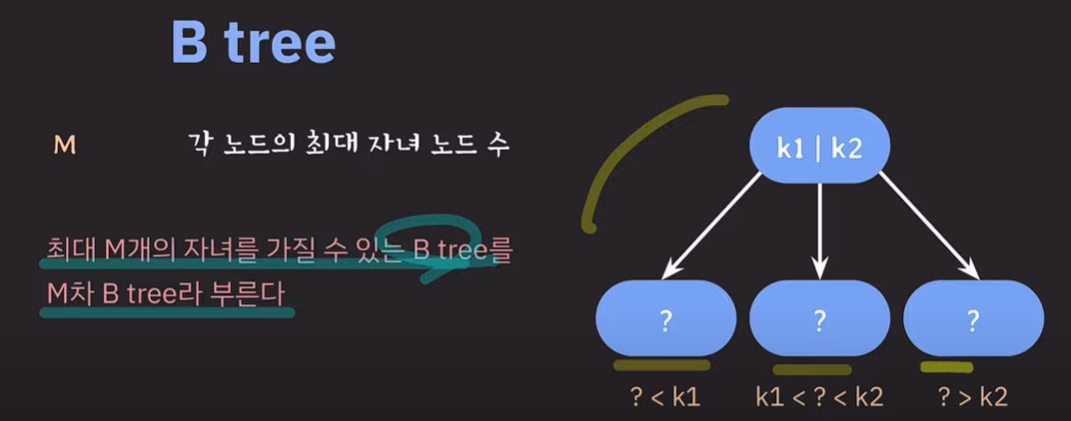
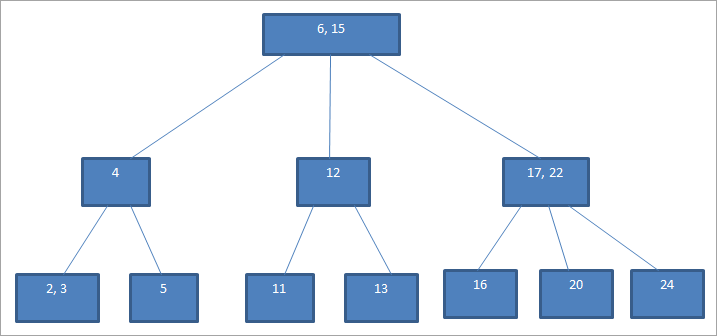
자녀노드가 최대 3개인 경우 3차 B tree

M-1

각 노드의 최대 key 수

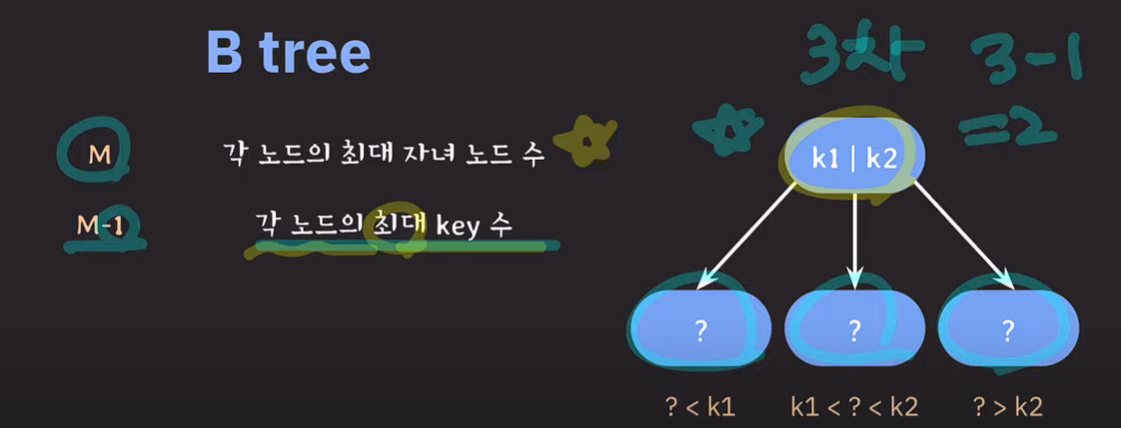
3차 B tree의 경우 최대 자녀 노드의 수가 3이고, 노드의 key의 갯수는 3-1 = 2이다.

M/2

각 노드의 최소 자녀 노드 수

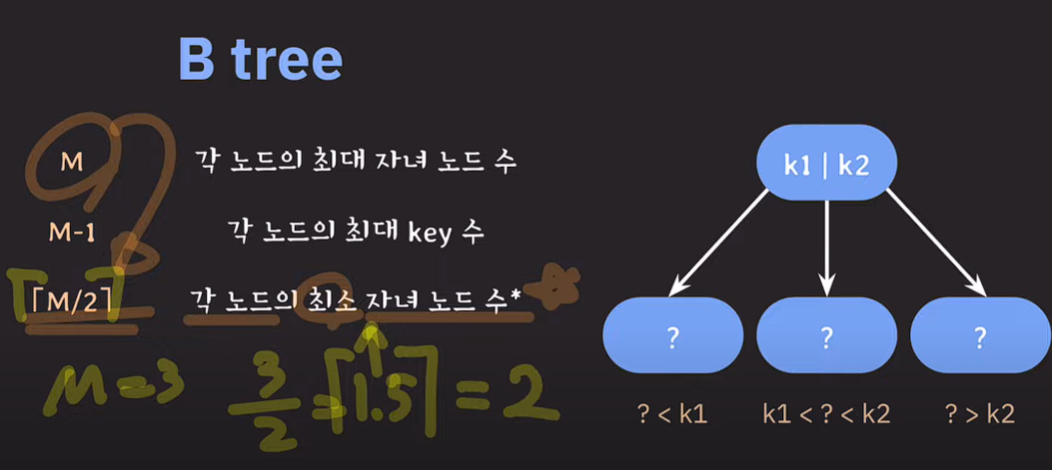
3차 B tree 3/2 = 1.5 올림 ==> 3차 B tree의 경우 자녀 최소 노드의 갯수는 2이다. 단, root node와 leaf node의 경우는 제외한다.
leat node는 자녀가 없는 노드를 뜻하고, root node는 이 규칙의 예외이다.

[M/2]-1

각 노드의 최소 key 수

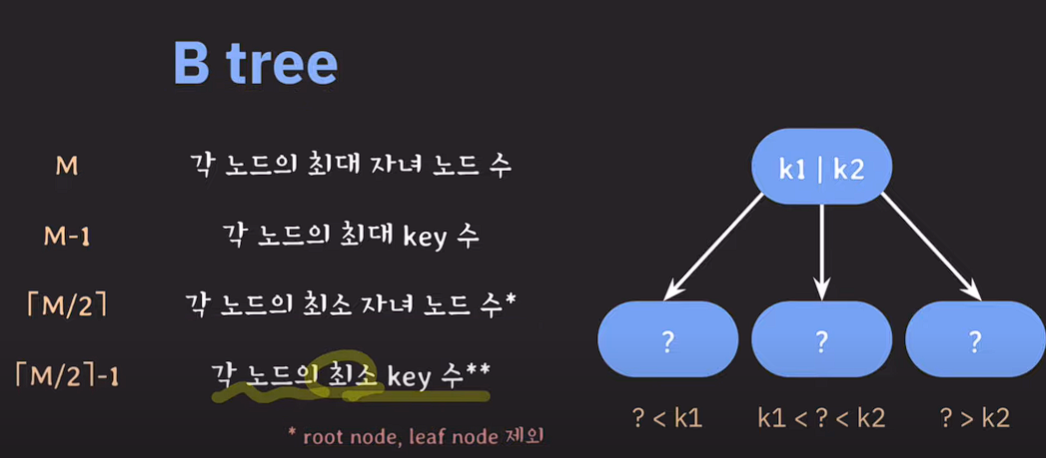
단, root node는 제외한다.

규칙

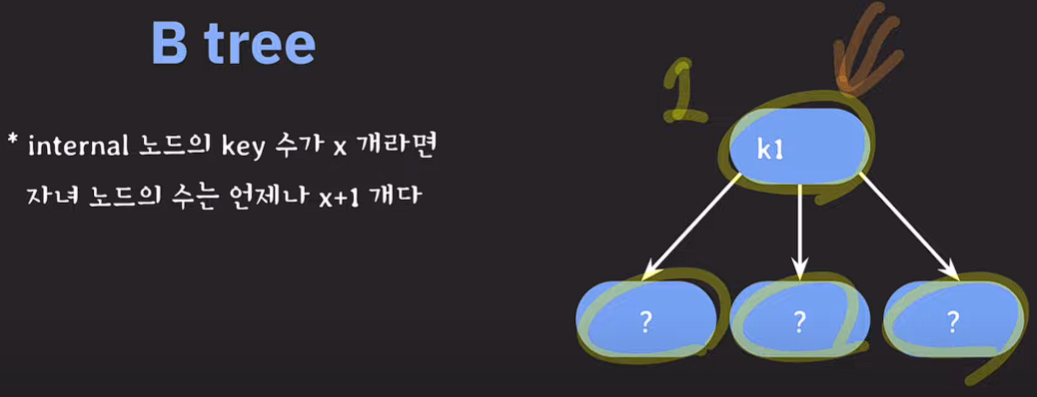
위와 같은 트리는 B tree에 존재할 수 없다.
internal 노드의 key 수가 x개라면 자녀의 노드수는 언제나 x+1개다.
key가 2개일 경우 자녀 노드는 3개이고, key가 1개 이면 자녀 노드는 2개이다.

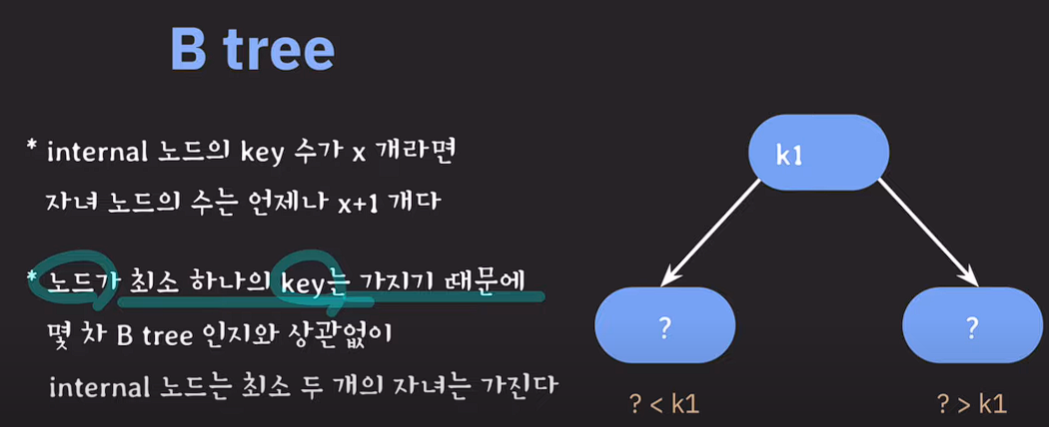
leaf 노드를 제외한, internal 노드는 반드시 key값이 존재하기 때문에 몇차 B tree 인지와 상관없이 internal 노드는 최소 두 개의 자녀를 가진다.
M이 정해지면 root 노드를 제외하고 intenral 노드는 최소 [M/2]개의 자녀 노드를 가질 수 있게 된다.

이진 탐색 트리 : internal 노드의 경우 노드의 수 1개 또는 2개
leaf node의 경우 0개

데이터 삽입 방식

1. 데이터 추가는 항상 leaf 노드에 한다.
2. 노드가 넘치면 가운데 key(중간값)를 기준으로 좌우 key들은 분할하고 가운데 key는 승진한다.

3차 B tree 데이터 삽입

Key의 최대 개수(M-1) = 2
최소 자녀의 수([M/2]) = 2
key의 최소 개수([M/2]-1) = 1

add(1); add(15); add(2); add(5); add(30); add(90); add(20); add(7);
add(8); add(10); add(50); add(70); add(60); add(40);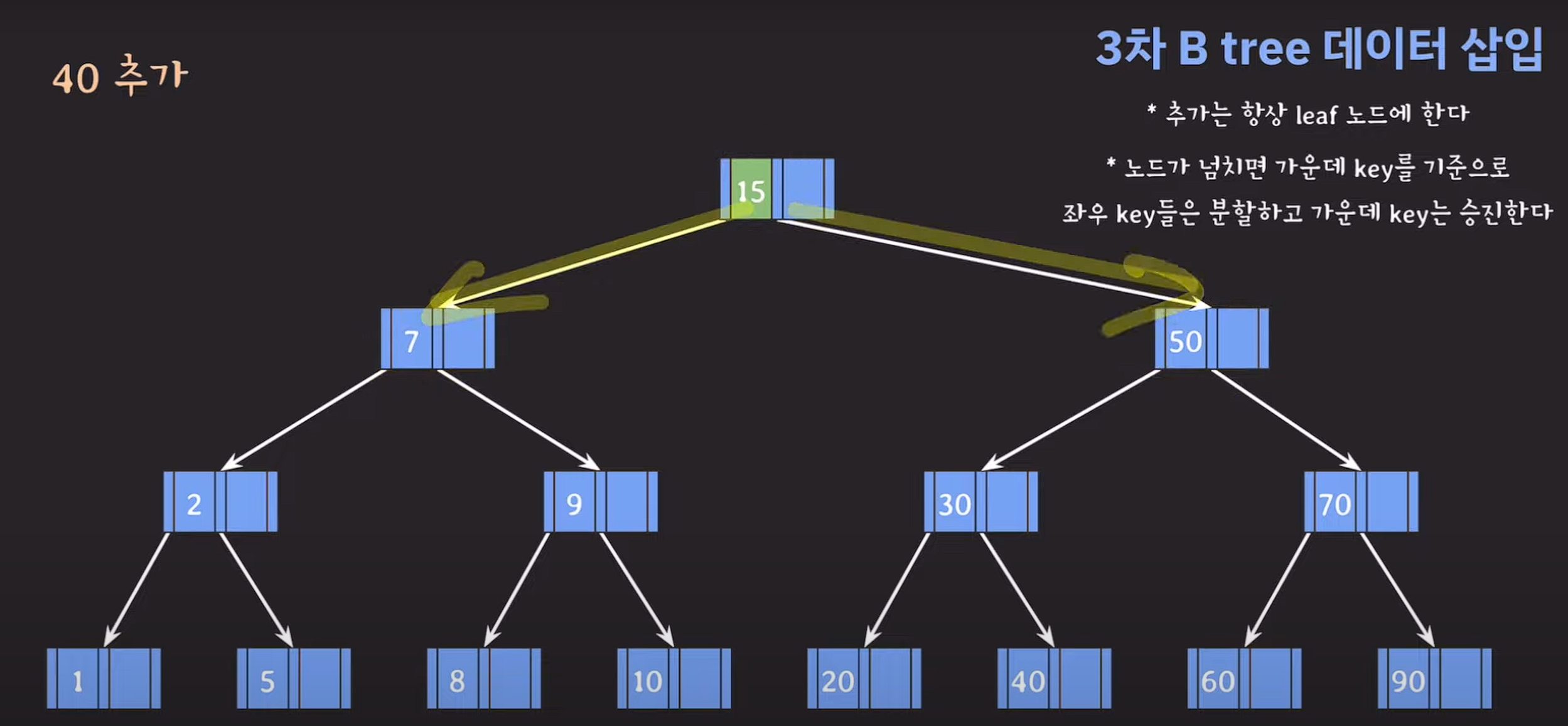

★모든 leaf node들은 같은 레벨에 있다 ==> balanced tree
검색 조회시 worst case O(logN)

이진 탐색 트리의 경우 자녀 노드가 0개 ~ 2개 즉, worst case O(N)
탐색 후 leaf node인지 아닌지 알 수 있다. 하지만 B tree는 항상 leaf node들이 같은 level에 존재하기 때문에 시간복잡도가 일정하다.

출처 : 쉬운코드 유튜브

데이터 삭제 방식

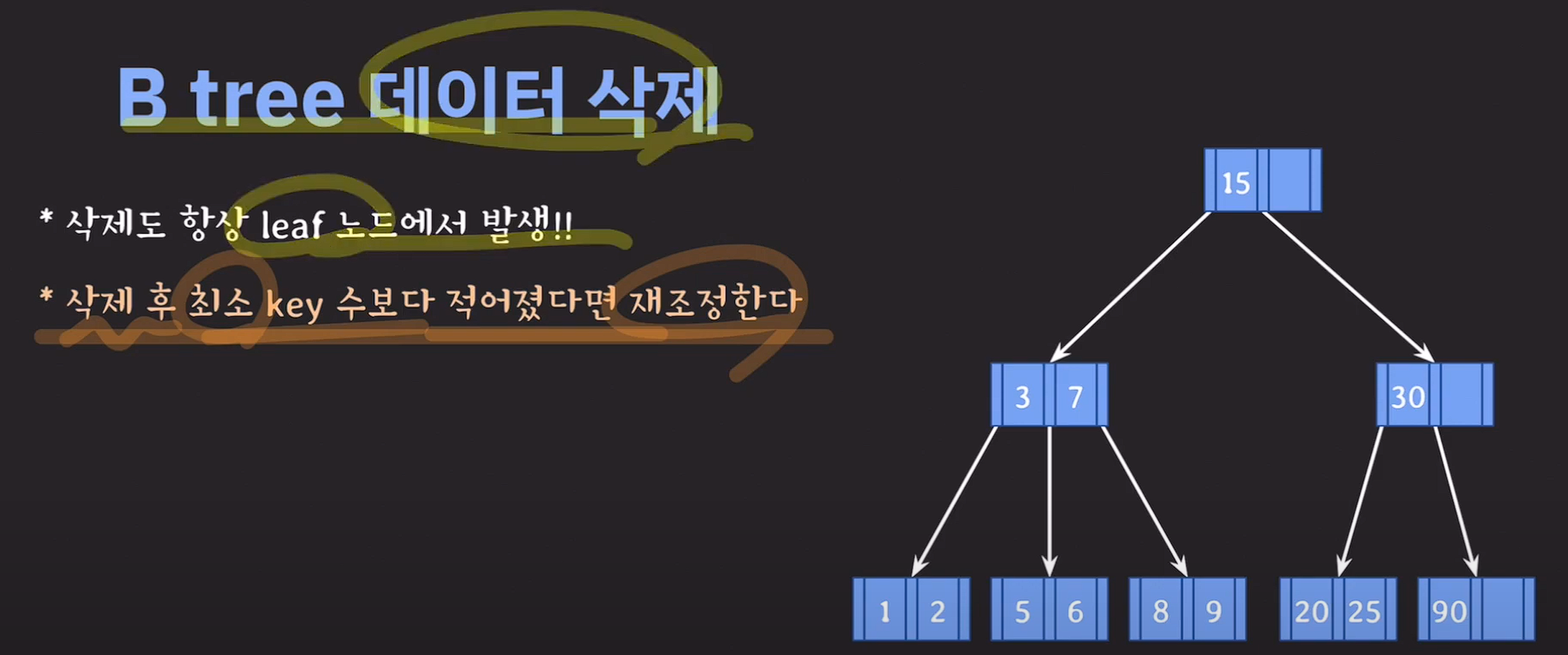
1. 삭제는 항상 leaf node에서 발생한다.
2. 삭제 후 최수 key 수 보다 적어졌다면 재조정한다. [M/2]-1
   3차 B tree에서 최소 key의 갯수는 1개 이다.

delete(6); delete(5);

키의 재조정

1.key 수가 여유있는 형제의 지원을 받는다.

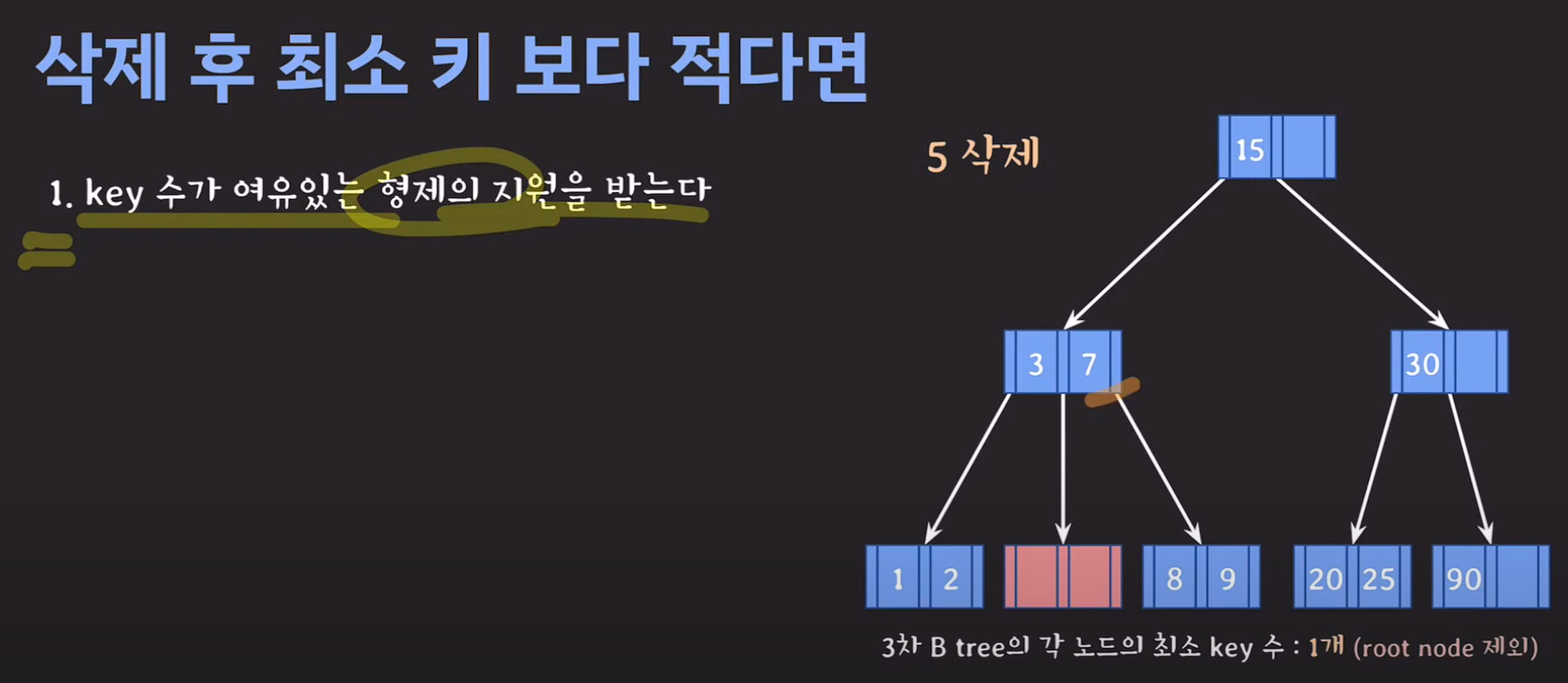
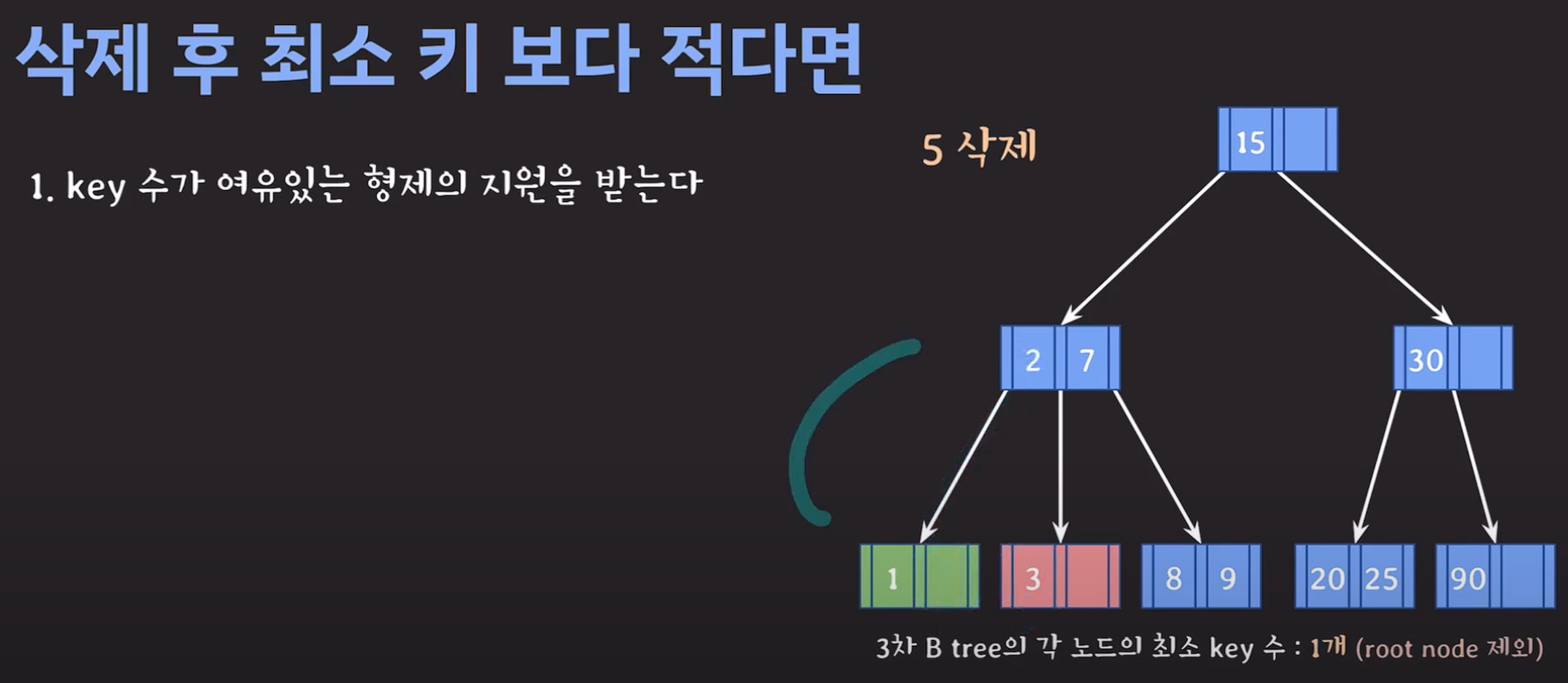
delete(3);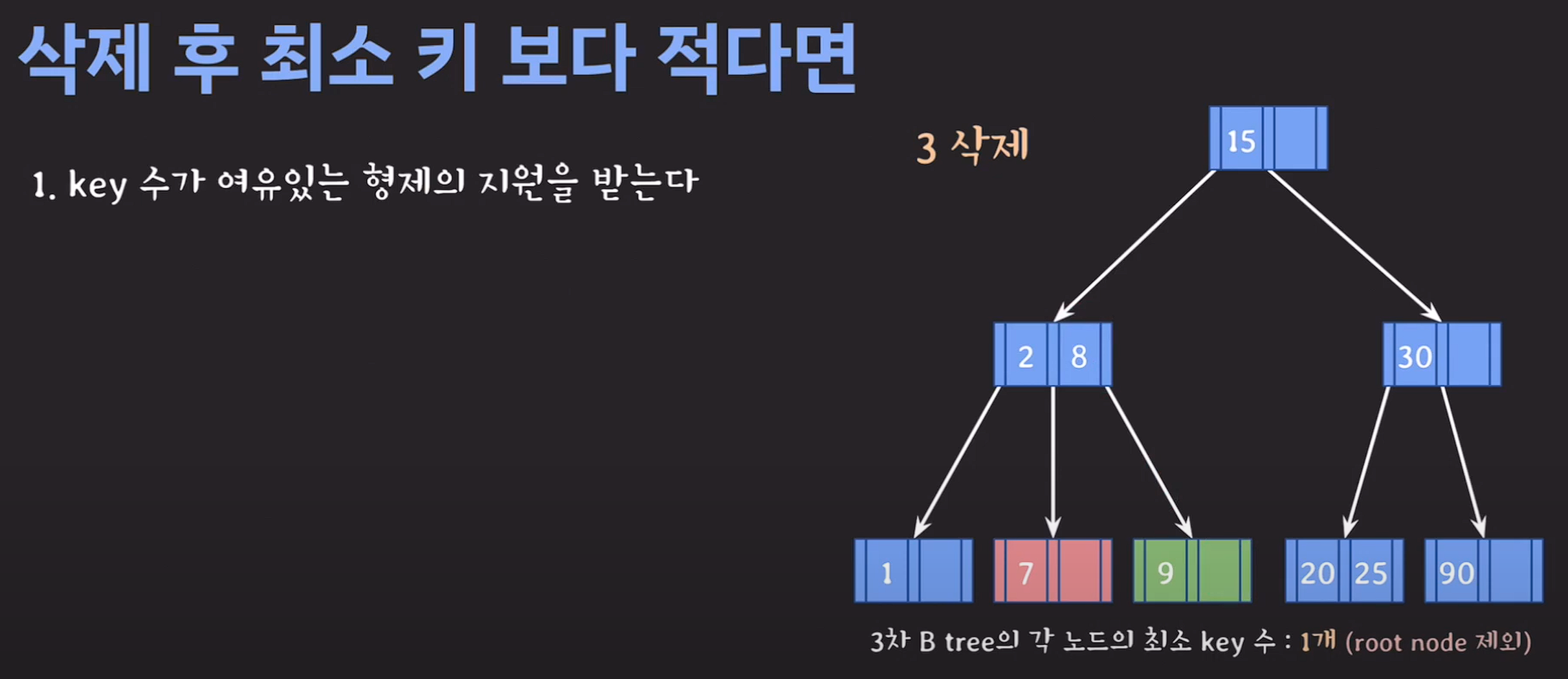

정리 :

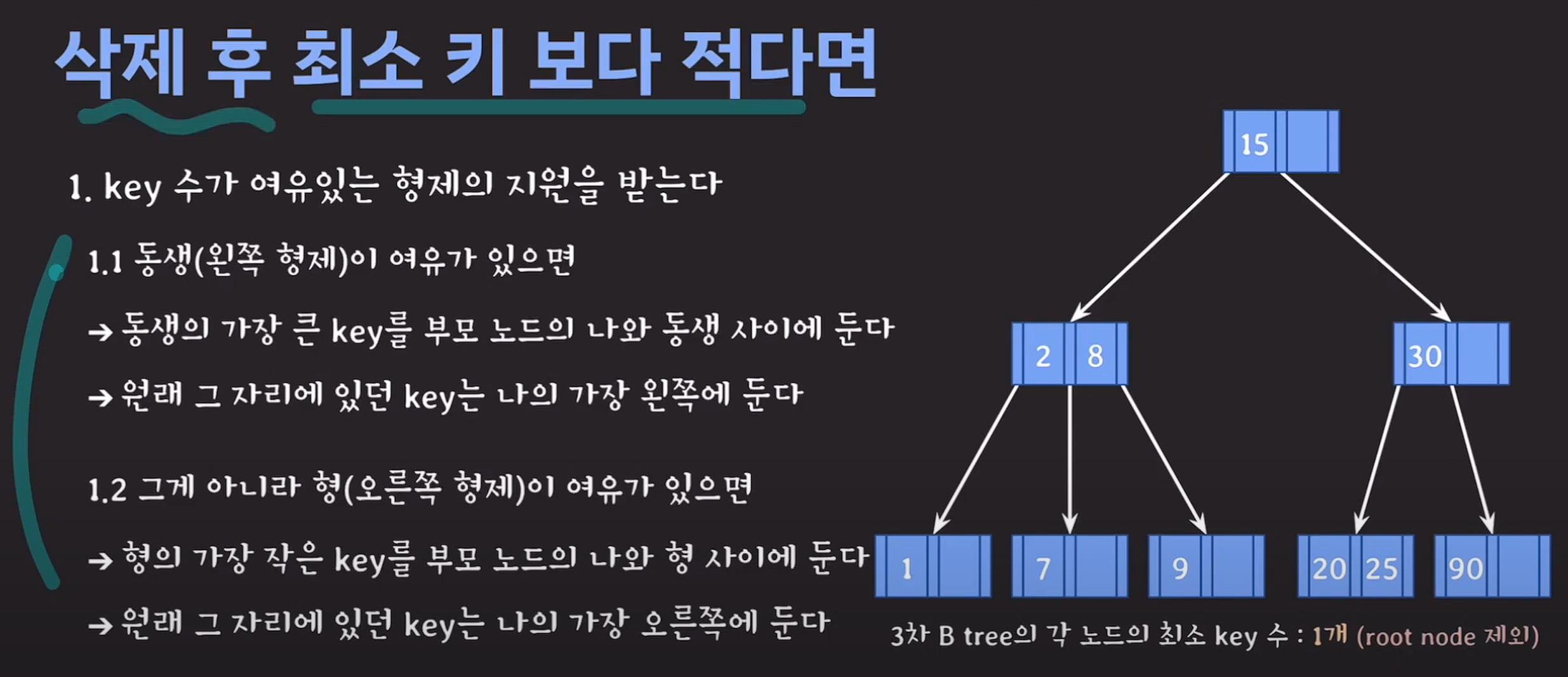
2.1번이 불가능하면 부모의 지원을 받고 형제와 합친다.

delete(7);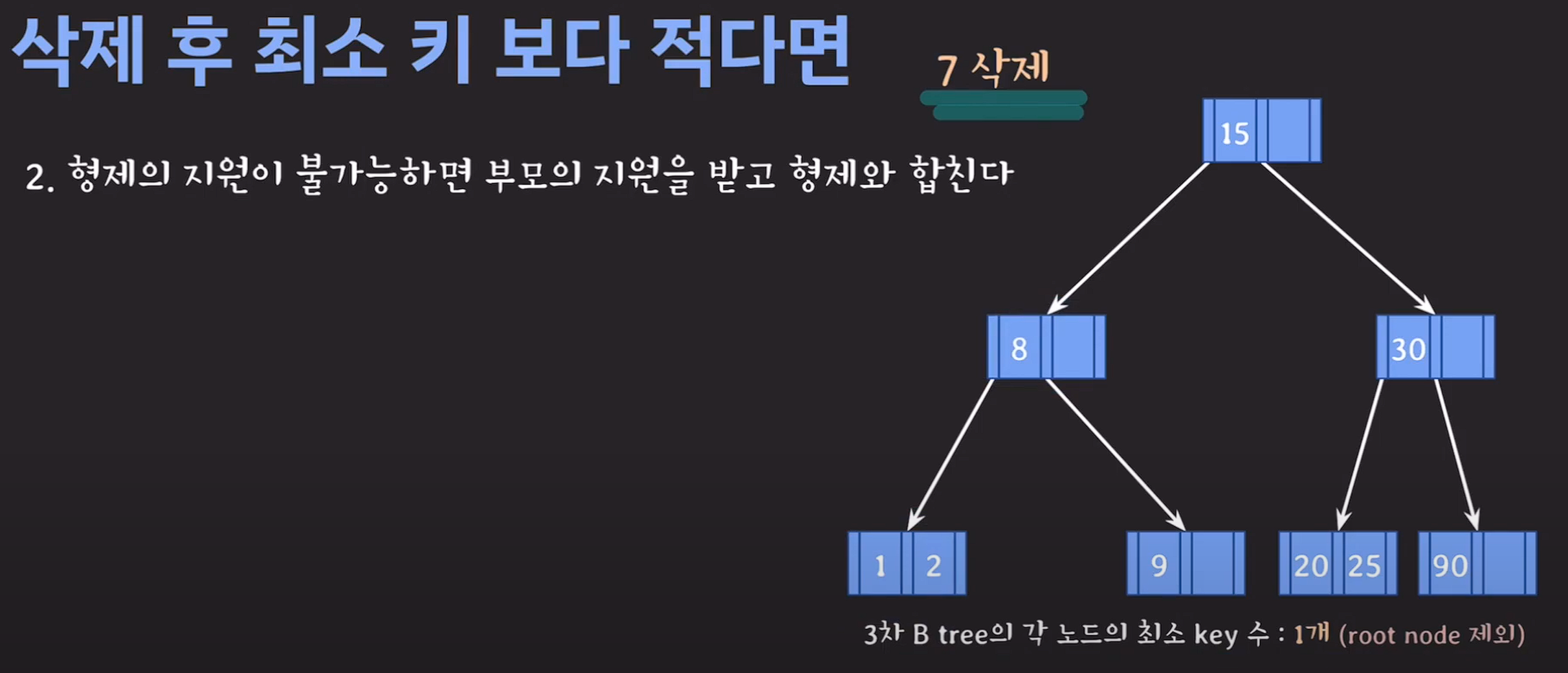

delete(2); delete(1);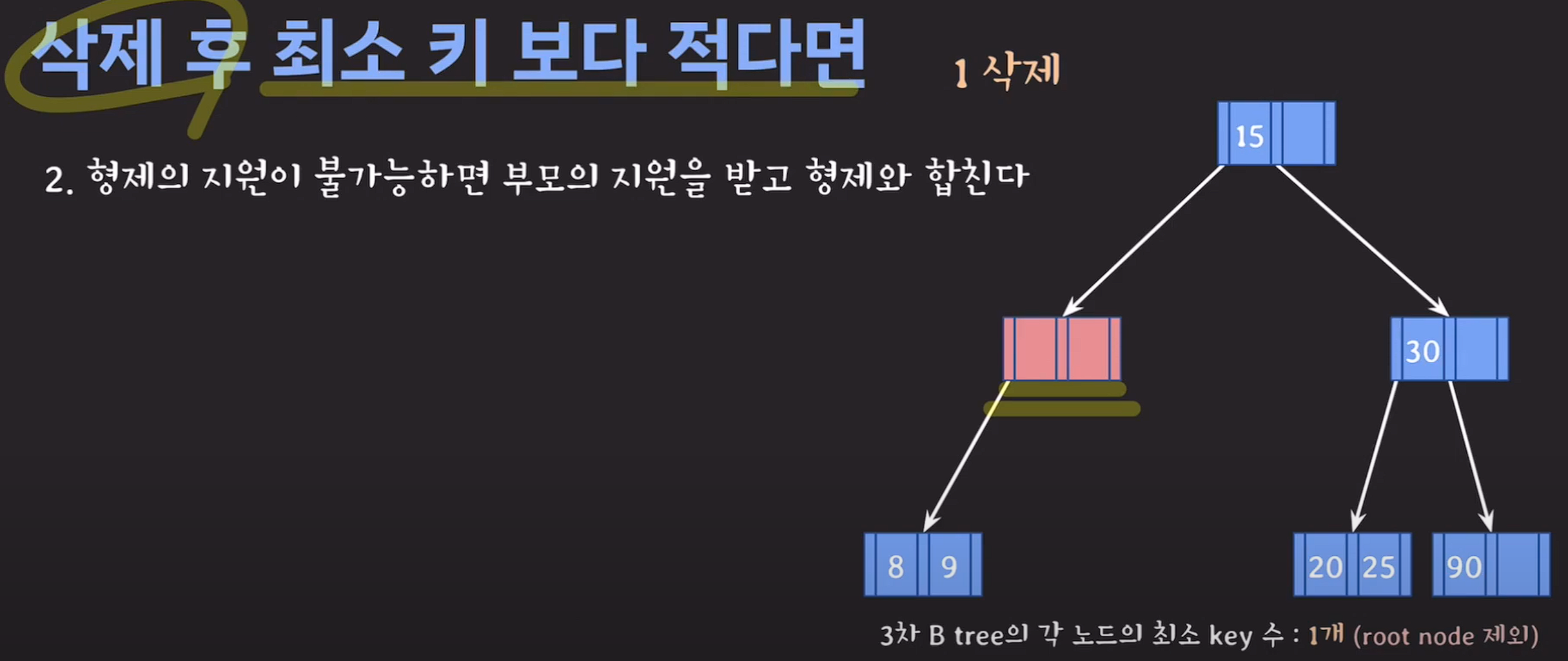

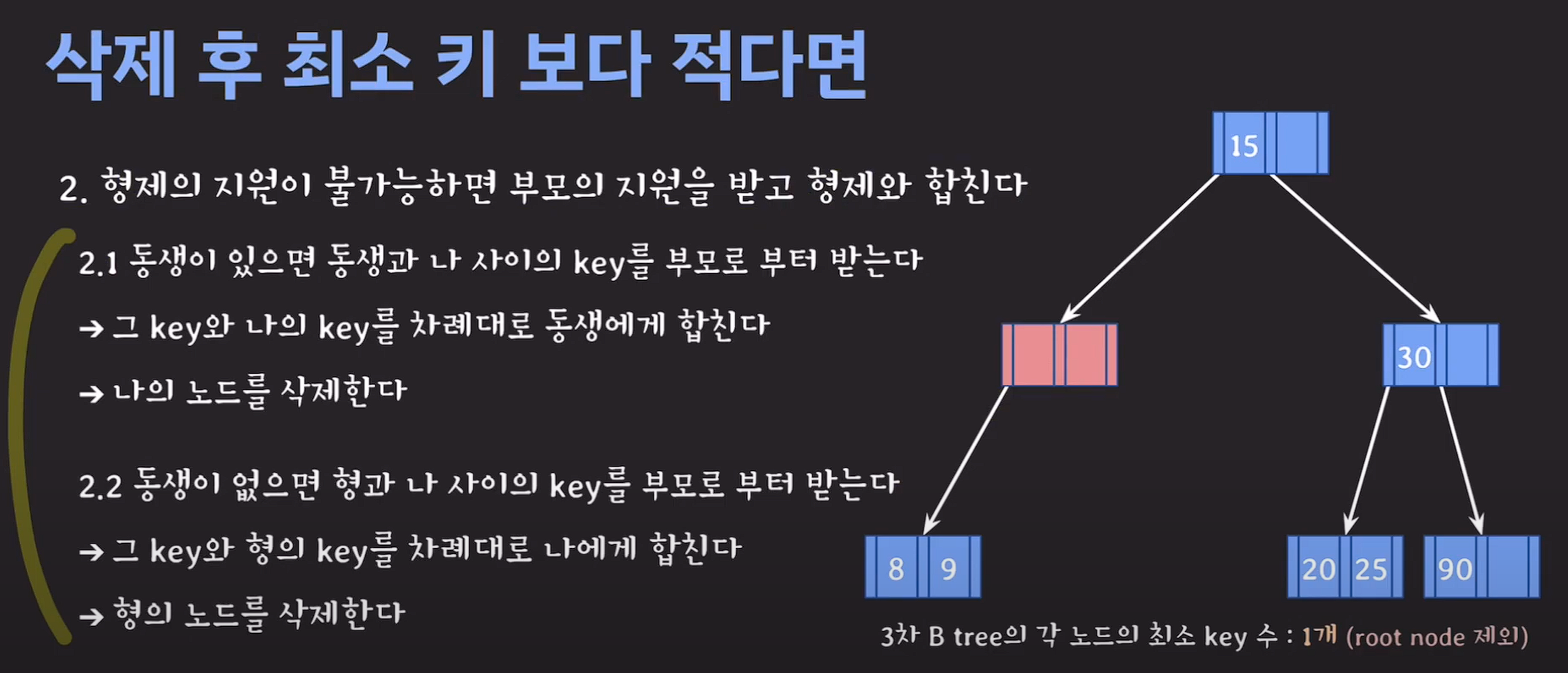
3.2번 후 부모에 문제가 있다면 거기서 다시 재조정한다.

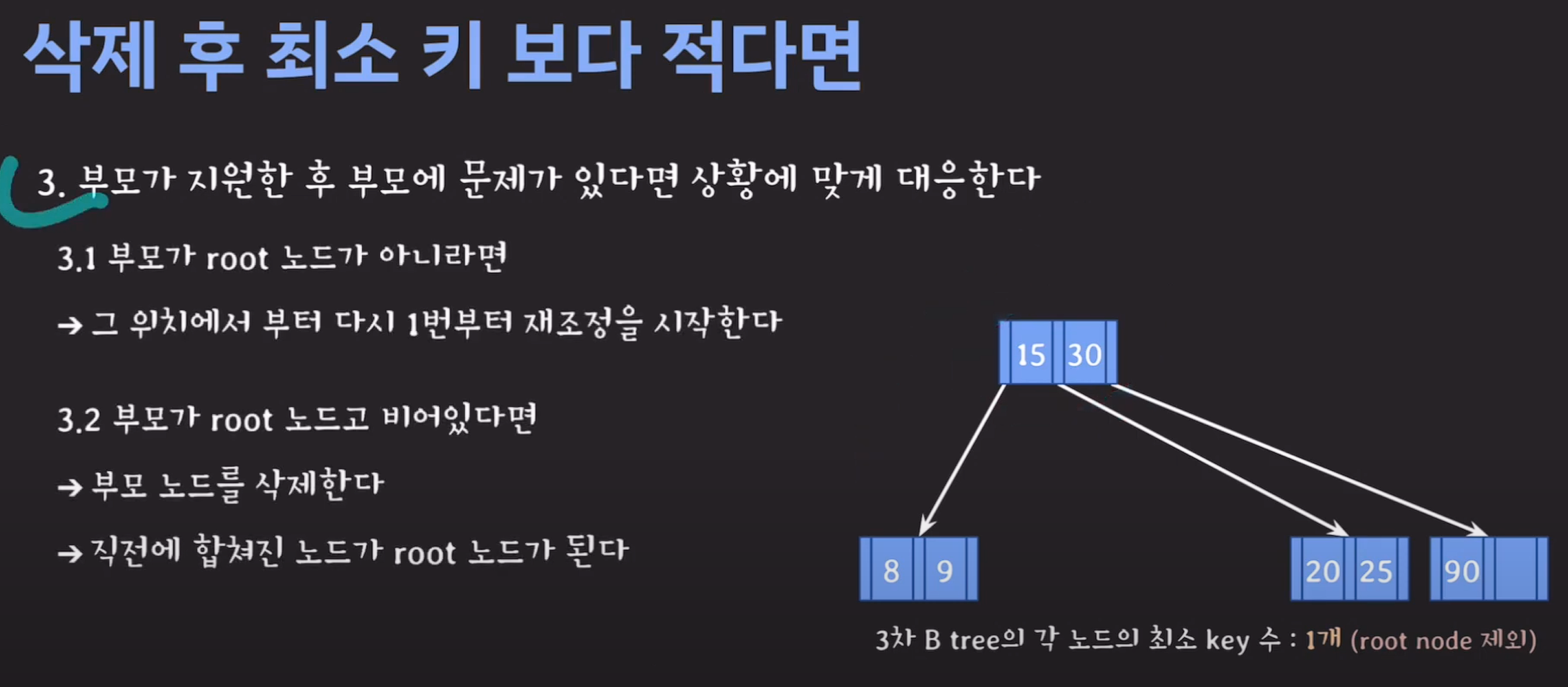
internal 노드 데이터 삭제

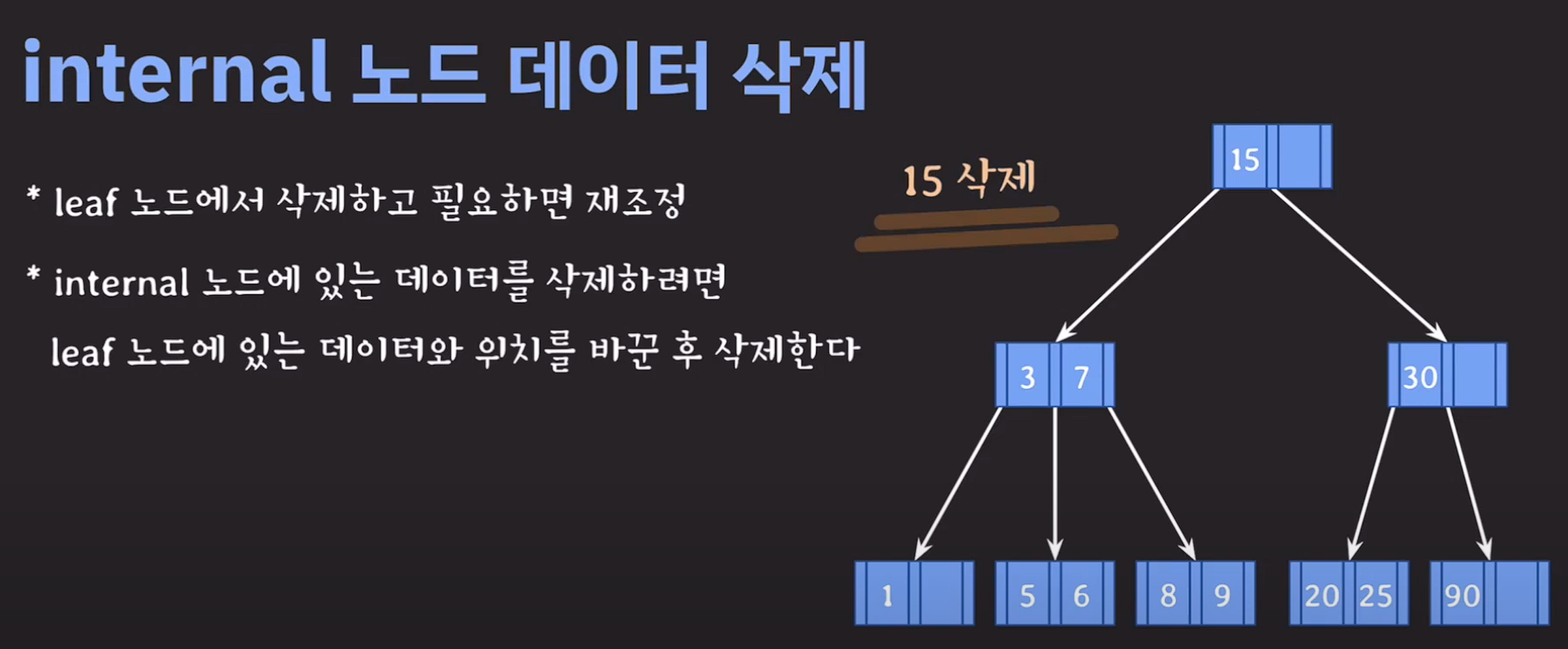
issue) 어떤 데이터와 바꿔야 하는가? 선임자 또는 후임자

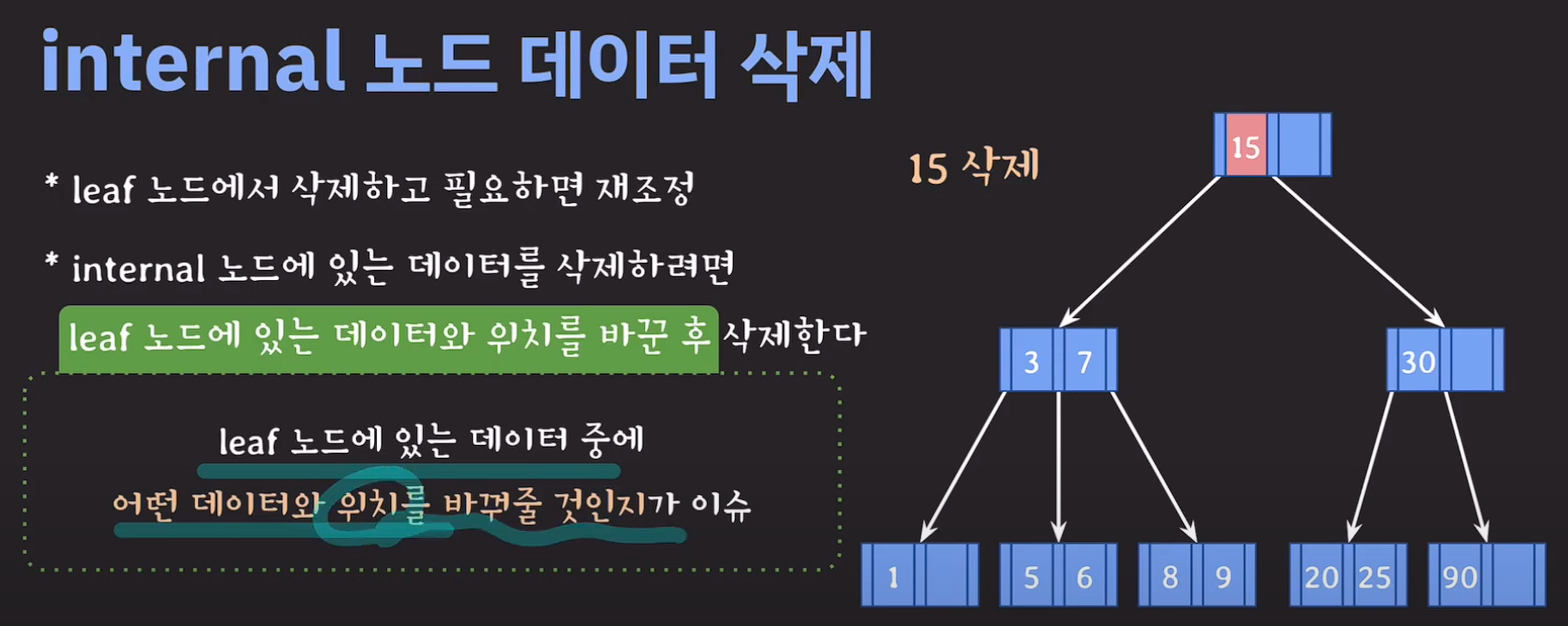
delete(15);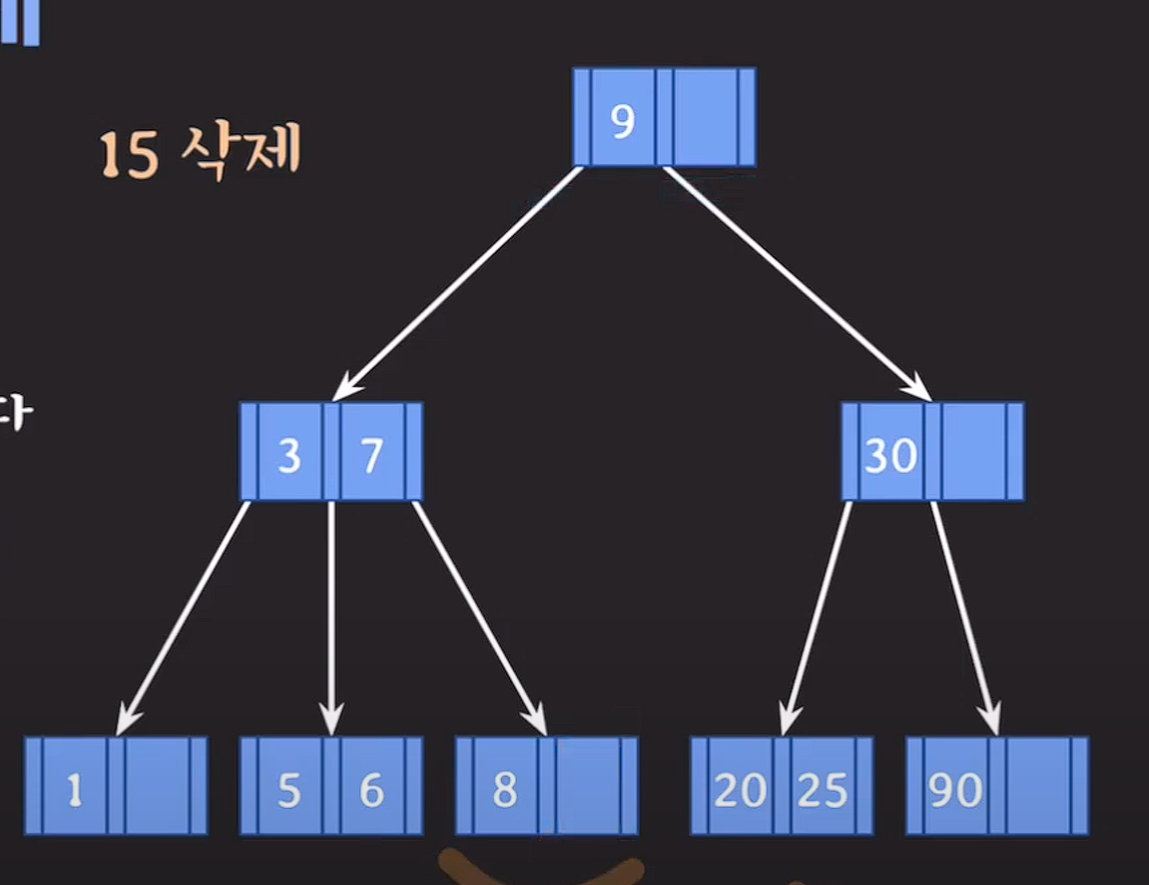

삭제 예제

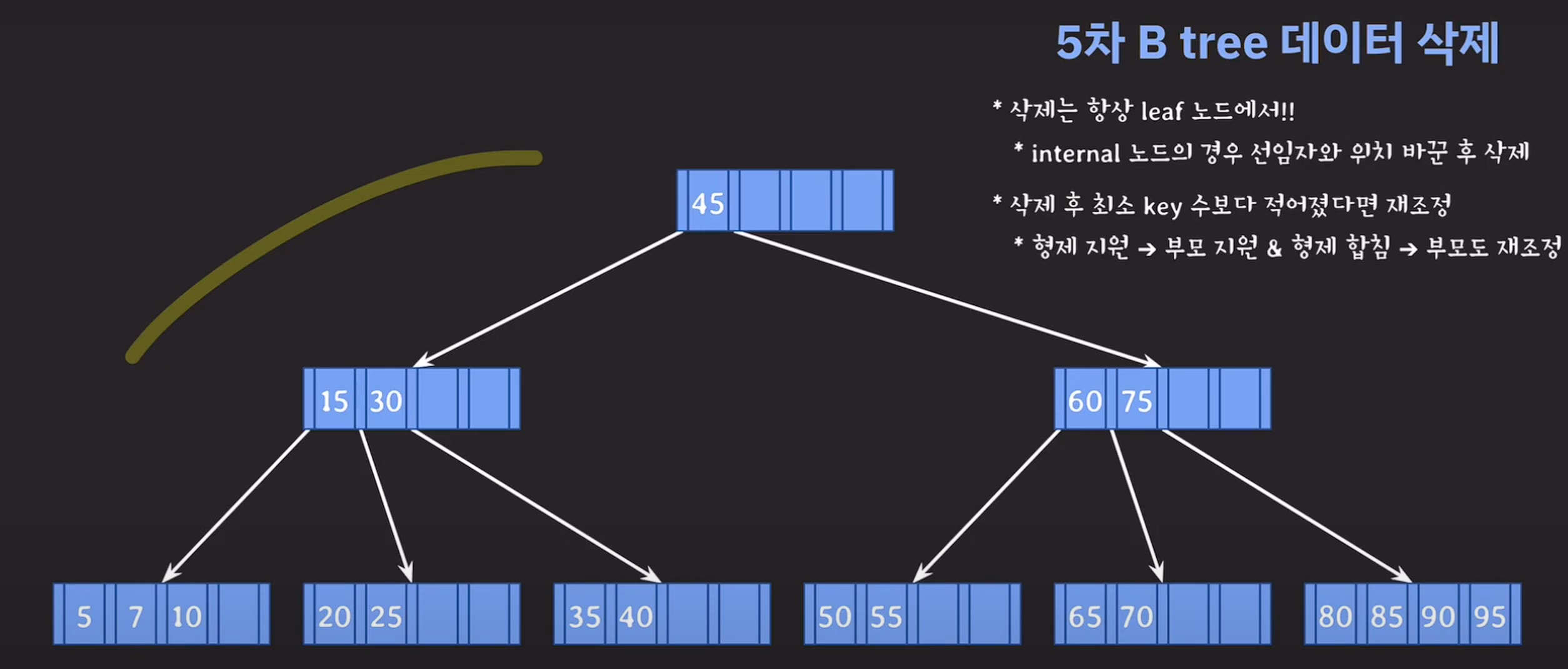
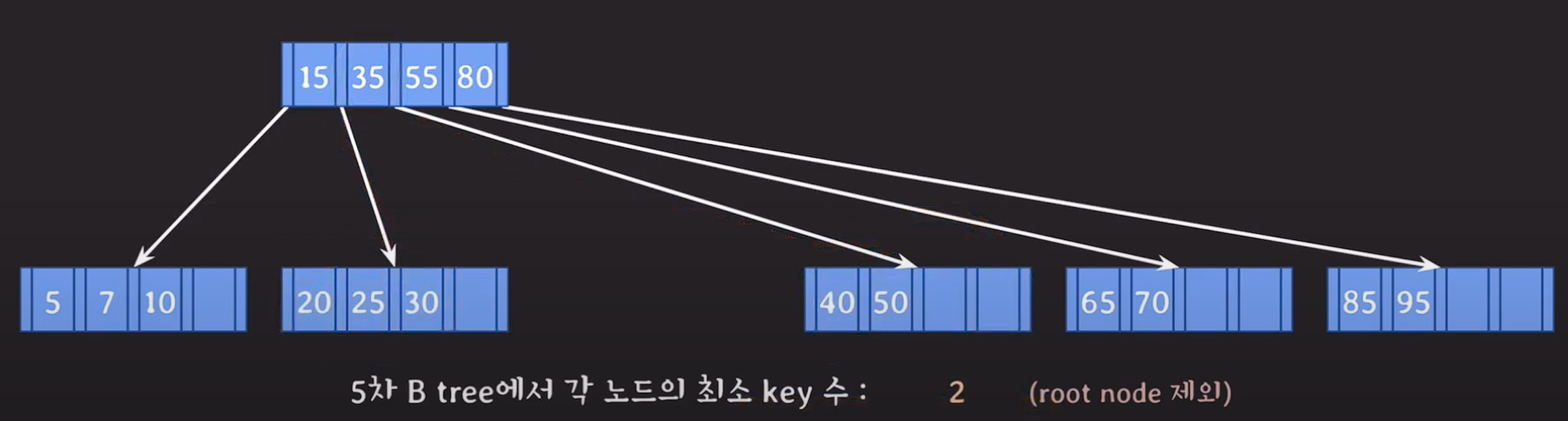
key의 갯수 4개 ==> 5차 B tree
최소 key 갯수 [M/2]-1 ==> 2개
key의 갯수가 1개일때 재조정해야한다.

delete(90); delete(75); delete(45); delete(60);
// 형제 또는 부모의 지원을 받는다.
// 자식노드에 있는 값 가져오면 안된다.

출처 : 쉬운코드 유튜브