Red-Black tree

개념

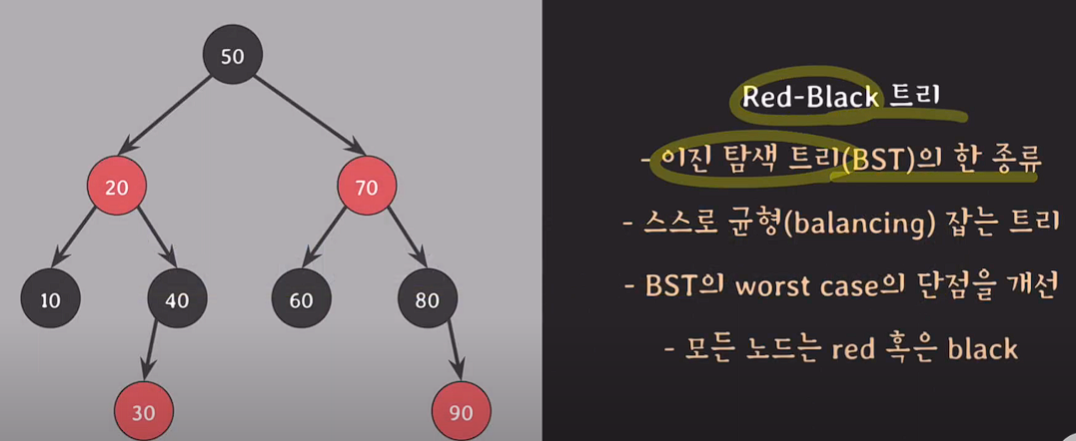
1. 이진 탐색 트리(BST)의 한 종류
2. 스스로 균형(balancing) 잡는 트리
3. BST의 worst case의 단점을 개선 O(N) > O(logN)
4. 모든 노드는 red 혹은 black

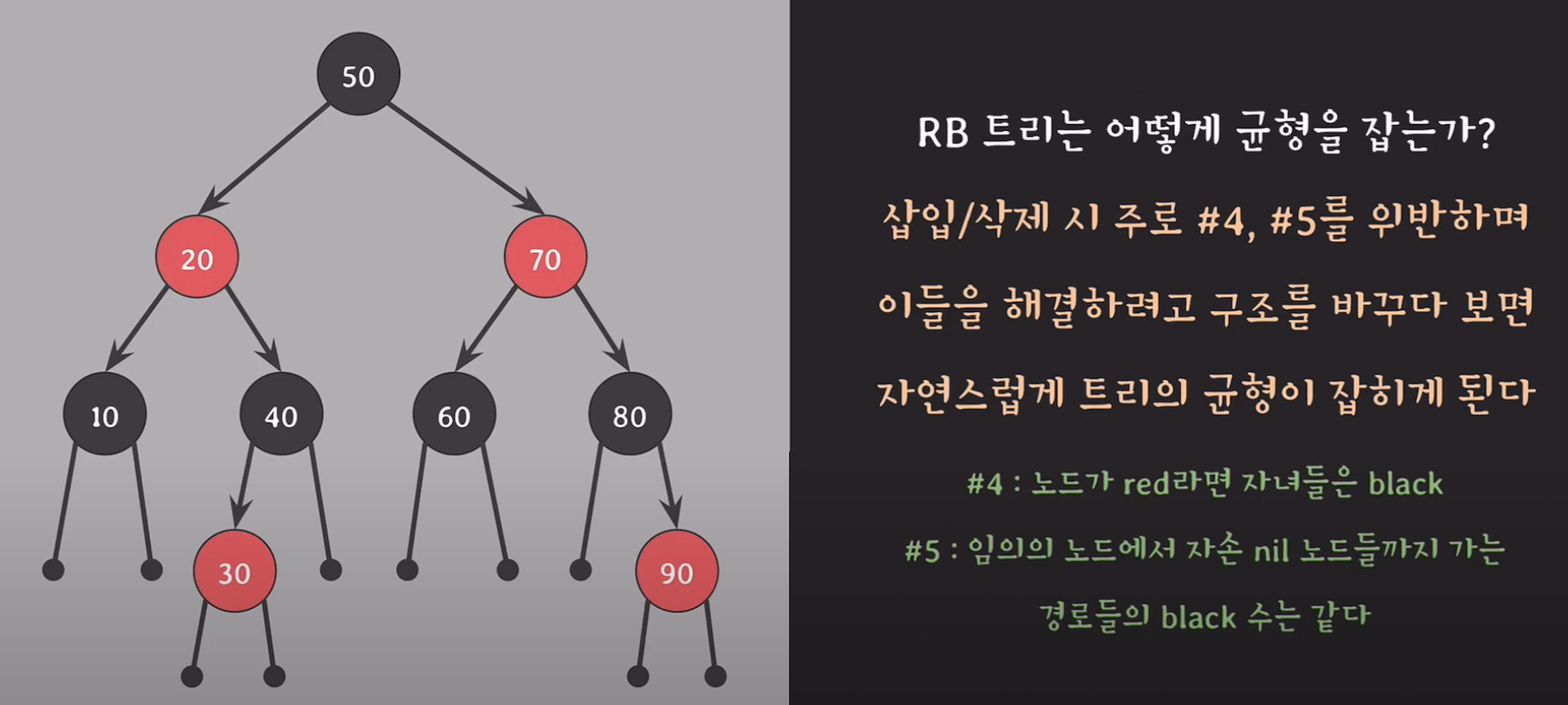
속성

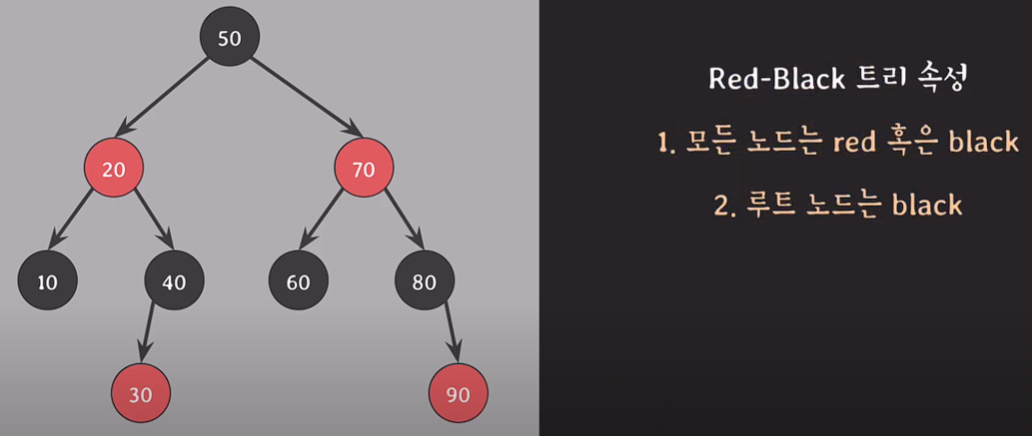
1. 모든 노드는 red 혹은 black
2. 루트 노드는 black
3. 모든 nil노드는 black
4. red의 자녀들은 반드시 black, red가 연속적으로 존재할 수 없다.

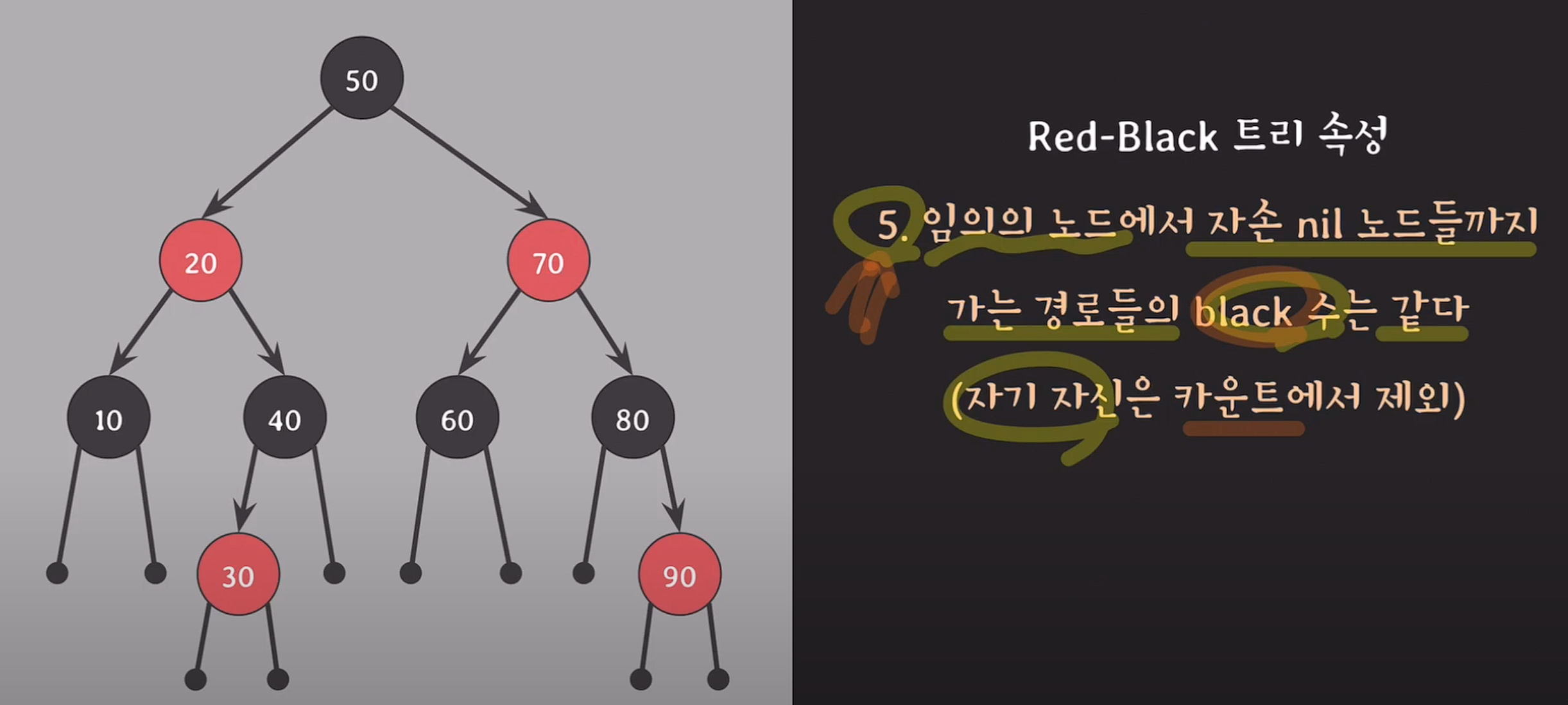
5. 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다.(자기 자신은 카운트에서 제외)

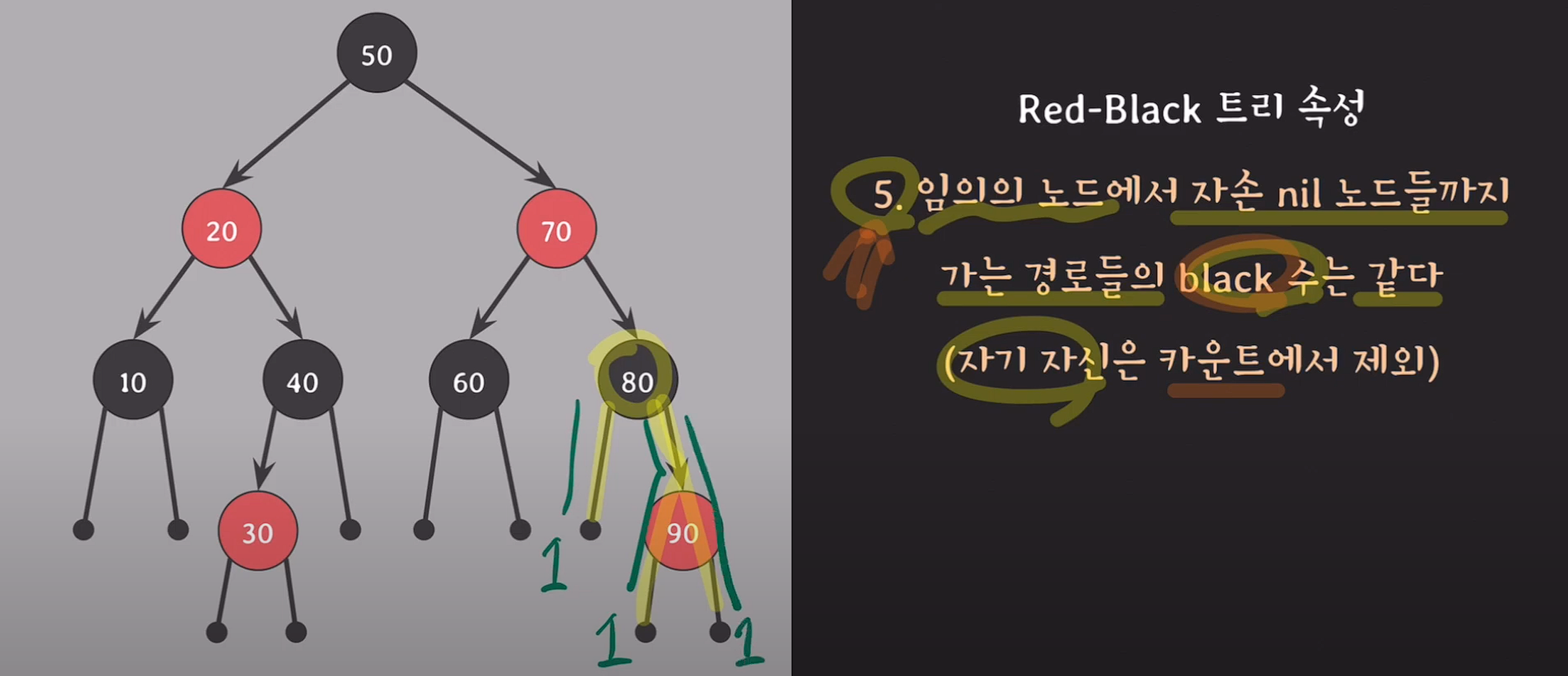
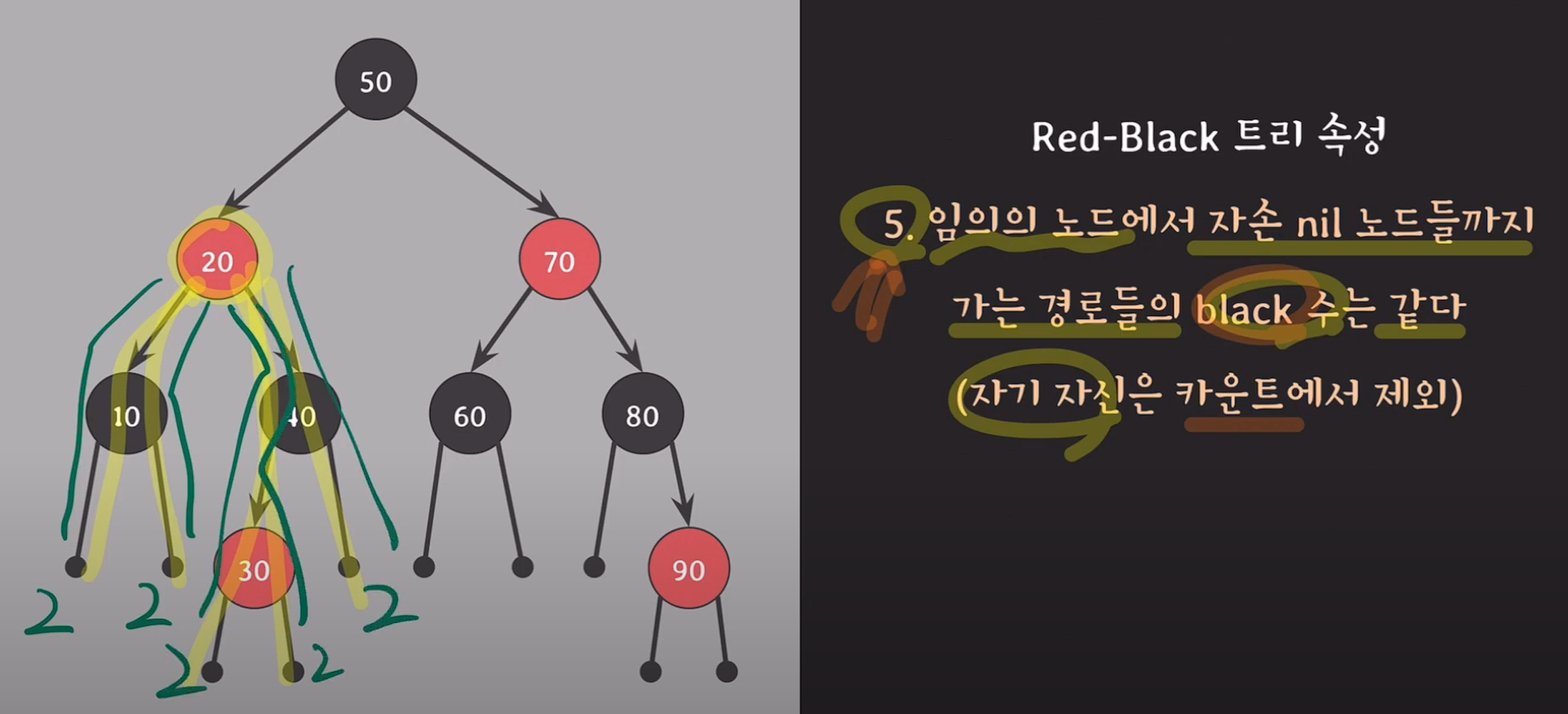
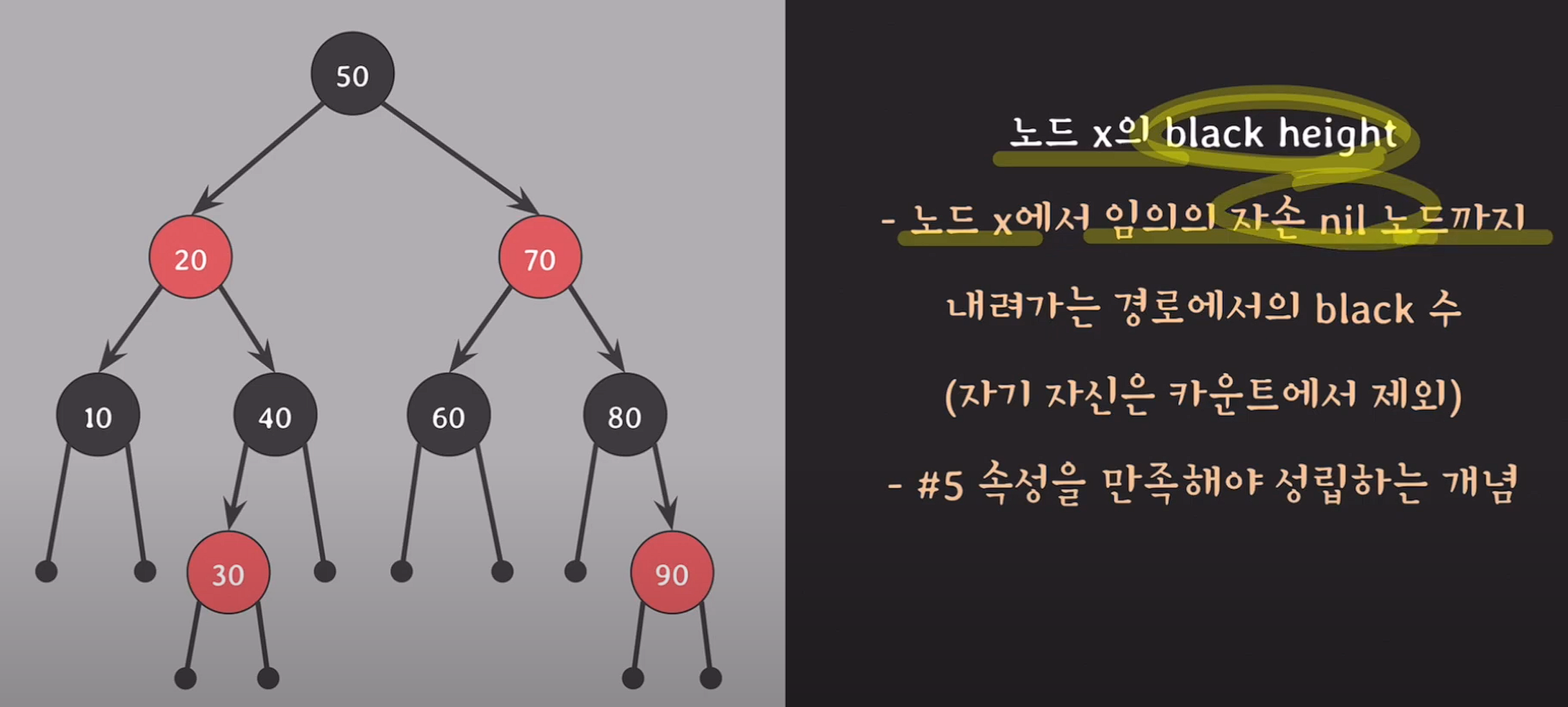
노드 x의 black height : 노드 x에서 임의의 자손 nil 노드까지 내려가는 경로에서의 black수(자기 자신은 카운트에서 제외), 5번 속성을 만족해야 성립하는 개념

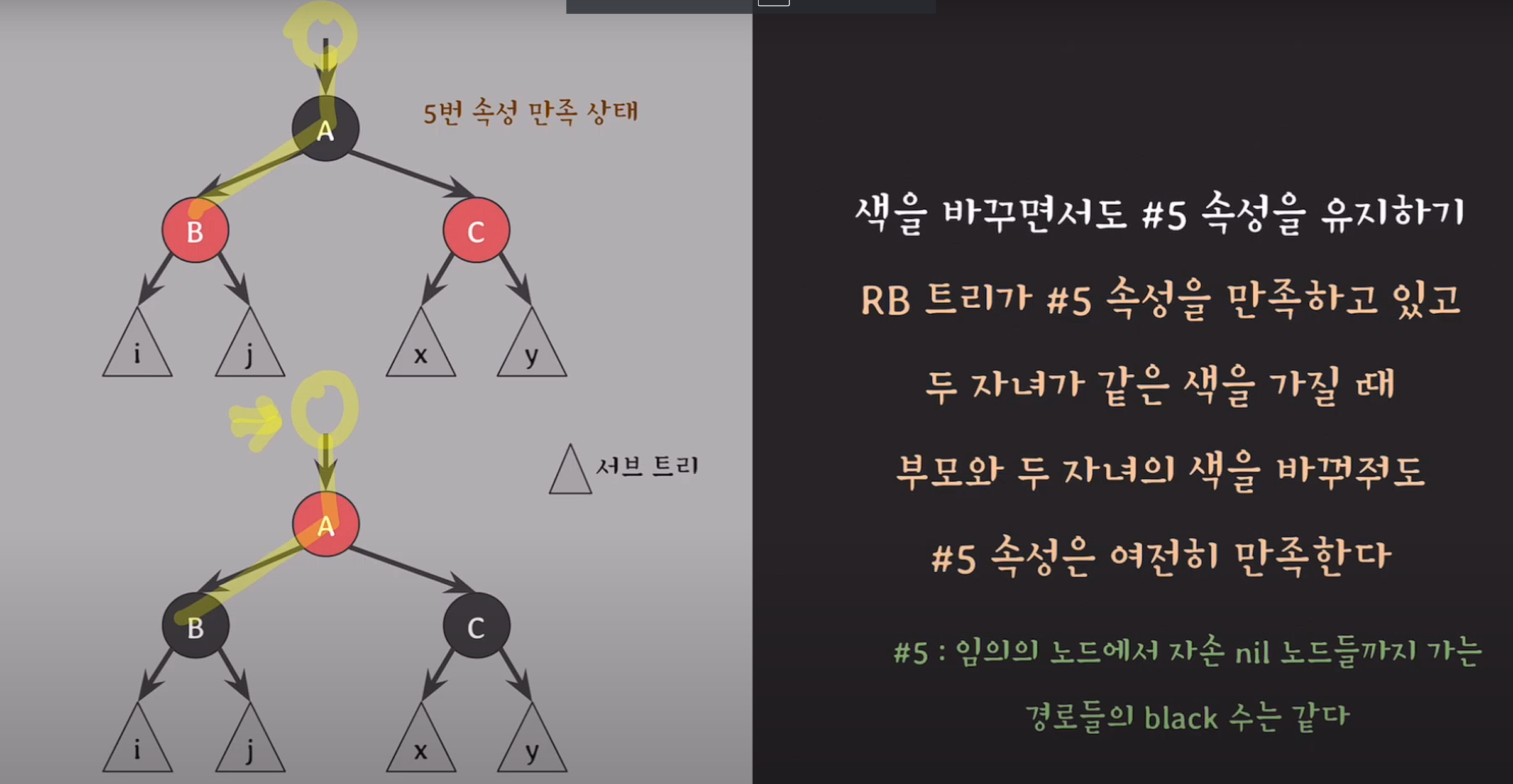
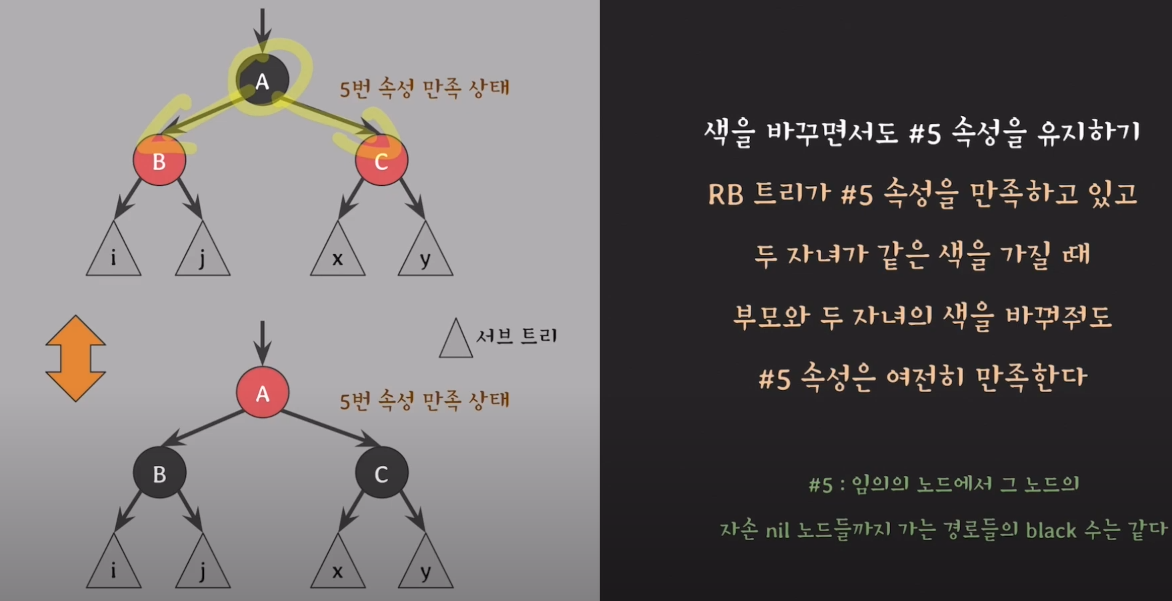
RB 트리가 #5 속성을 만족하고 있고 두 자녀가 같은 색을 가질 때 부모와 두 자녀의 색을 바꿔줘도 #5 속성은 여전히 만족한다.

==> nil노드 까지 가는 black의 수는 같다. A의 부모노드 기준 black의 수 유지.
A를 기준으로 양옆 +1씩 black의 수 증가.

nil node

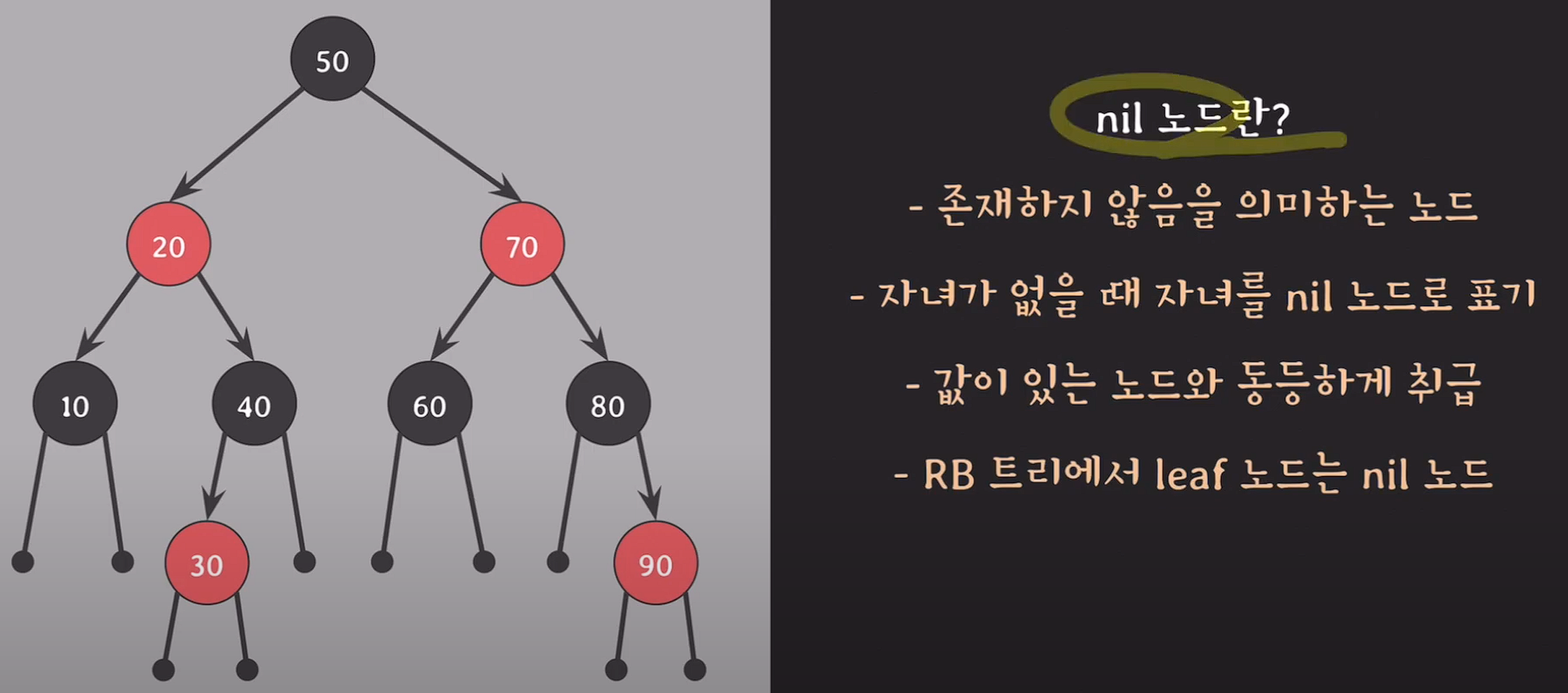
레드 블랙 트리에만 존재하는 개념
자녀가 없을 때 자녀를 nil 노드로 표기
ex) 40을 기준으로 왼쪽은 자녀가 있지만, 오른쪽은 nil 노드로 표시.
90을 기준으로 왼쪽, 오른쪽 모두 nil 노드로 표시
값이 있는 노드와 동등하게 취급한다.

Balancing

삽입

삽입 노드의 색 : 삽입하는 노드는 항상 red다.

insert(50);
// 삽입하는 50은 red로 저장되고,
// 자녀 노드는 nil 노드이다.

root node는 반드시 black이여야 하는데 추가된 50은 red이다. 색을 변경한다.

insert(20);
// 추가되는 20은 red이고
// 자손 노드는 모든 nil 노드로 black
// 모든 노드를 기준으로 nil 노드까지의 black수가 동일하다.
// 50을 기준으로 blakc height = 양옆 모두 1, 20 기준 양옆 1

삽입하는 노드는 왜 red 일까?

삽입 후에도 #5 속성을 만족하기 위해

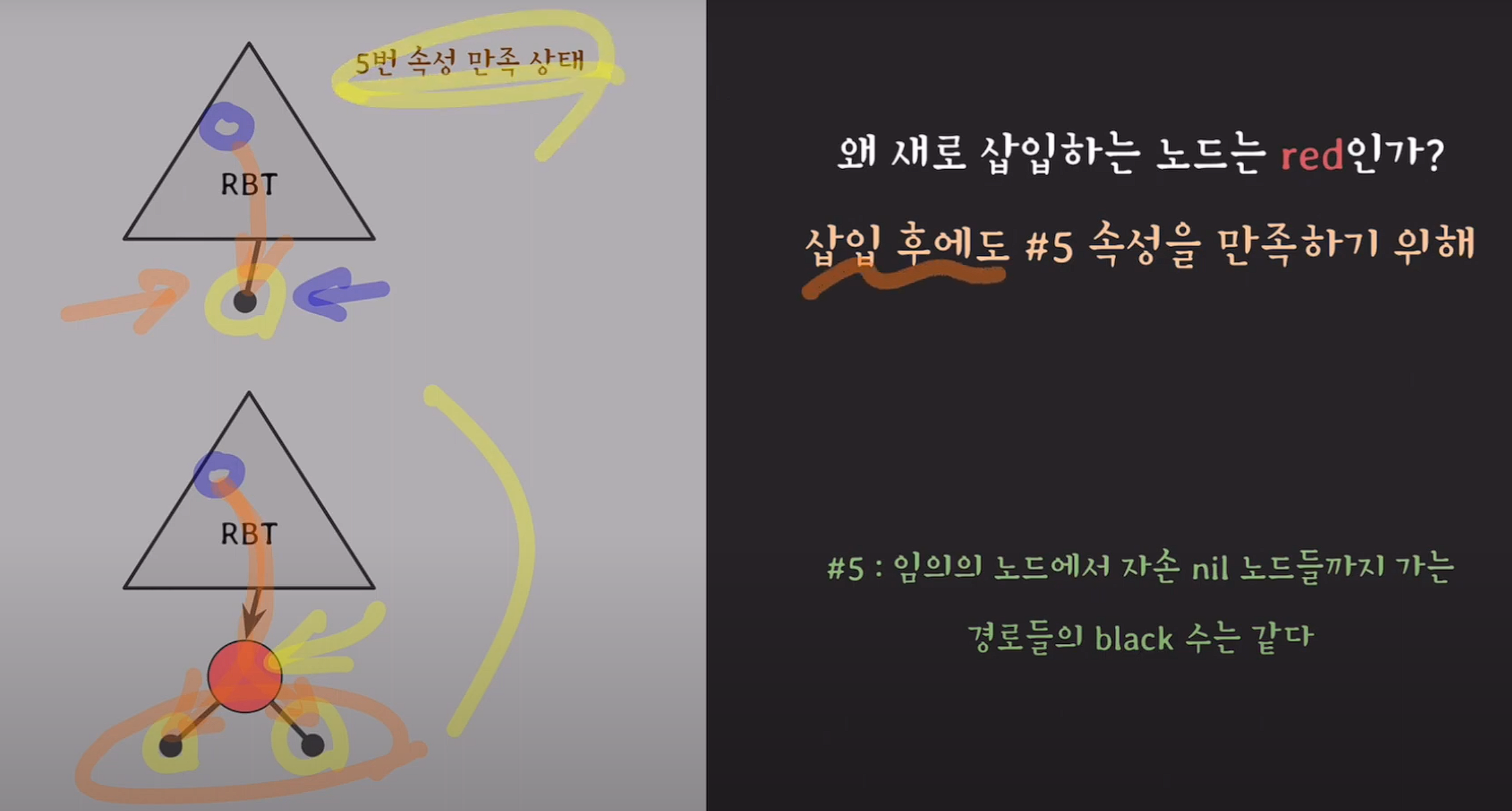
임의의 노드를 기준으로 red가 추가되고 red의 자녀가 모두 nil 노드이다.
양쪽 모두 black수는 그대로 유지되기 때문에 #5속성이 유지된다.

경우의수 1

insert(10);
// nil 노드 표시 생략.
// 새로 추가된 10은 red이지만, red의 자녀 노드들은 black이여야한다.
// 속성 위반

구조를 바꾸면서도 BST의 특징을 유지시키는 방법은 회전(로테이트)이다.

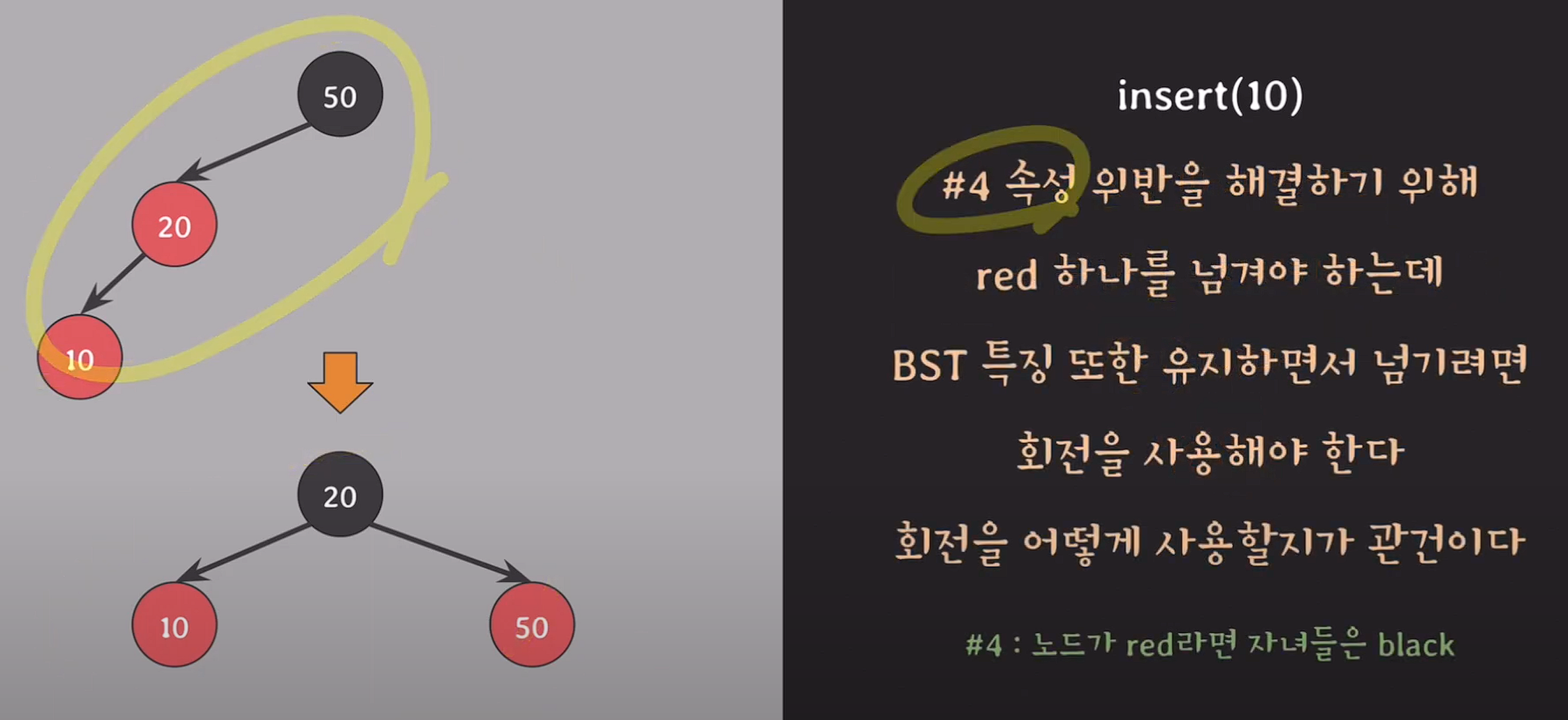
20을 기준으로 nil노드까지의 높이 양쪽 1, 10과 50을 기준으로 1

삽입된 red 노드가 부모의 왼쪽 자녀 & 부모도 red고 할아버지의 왼쪽 자녀
& 삼촌(=부모의 형제,sibling node)은 black이라면 부모와 할아버지의 색을 바꾼 후 할아버지 기준으로 오른쪽 회전한다.
==> 오른쪽 왼쪽을 바꿔도 성립한다.

경우의수 2

insert(40);
// 추가된 40은 red이고,
// 부모 20은 red, 자녀 40도 red 속성위반.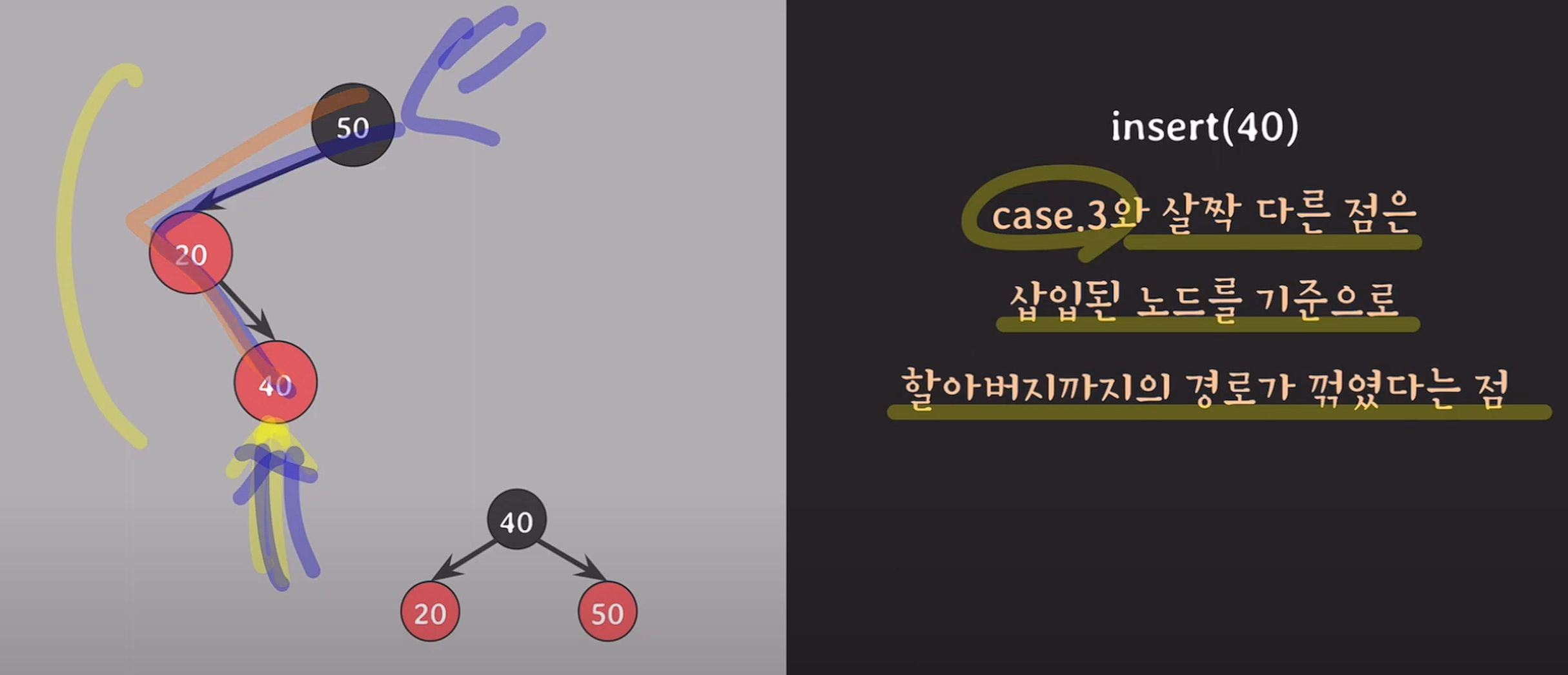

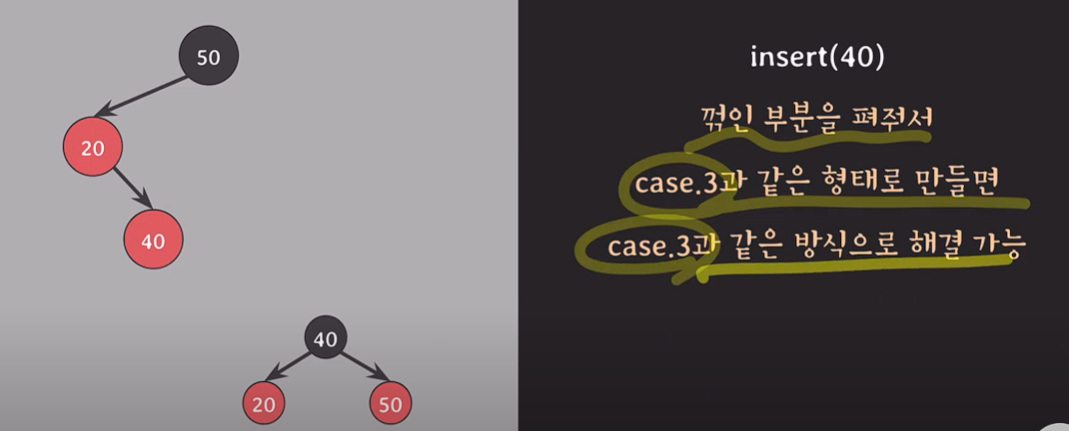
20을 기준으로 왼쪽으로 회전 시켜 꺽인 부분을 펴준다.

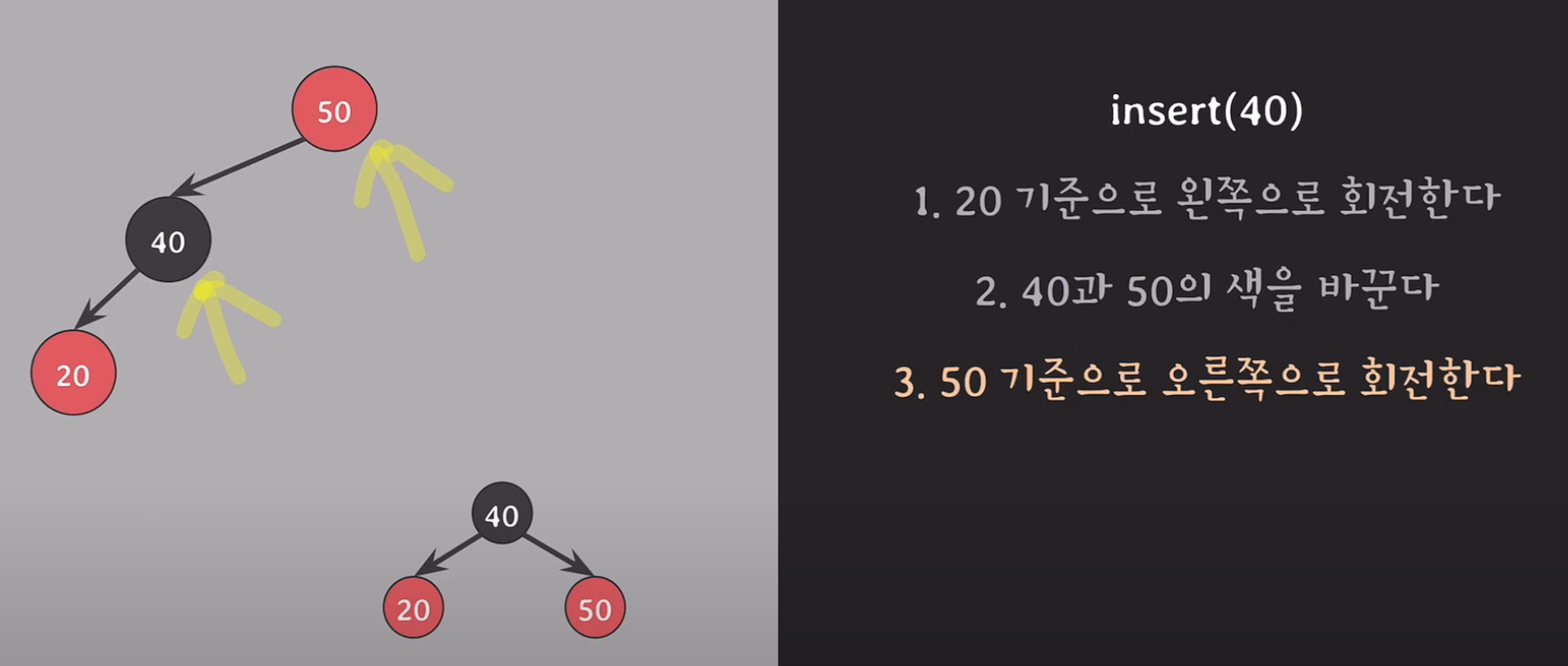
경우의수 3

insert(30);
// red 50의 자녀는 블랙이어야한다.
// red는 연속으로 나올 수 없다.

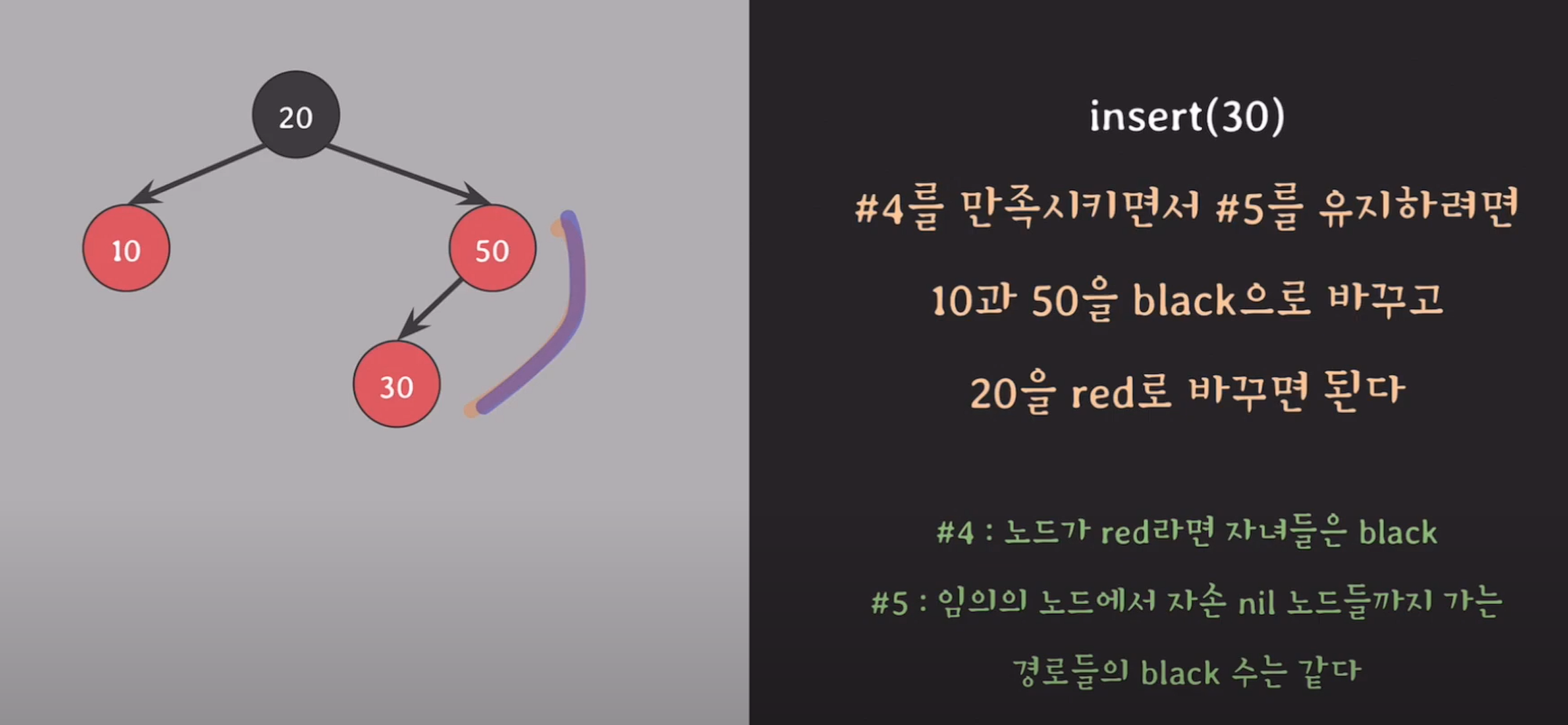
루트노드는 반드시 black이어야하고, black의 자녀가 black인것은 상관없다.

부모와 삼촌을 black으로 바꾸고, 할아버지를 red로 바꾼다.
그 후 할아버지에서 다시 확인을 시작한다.

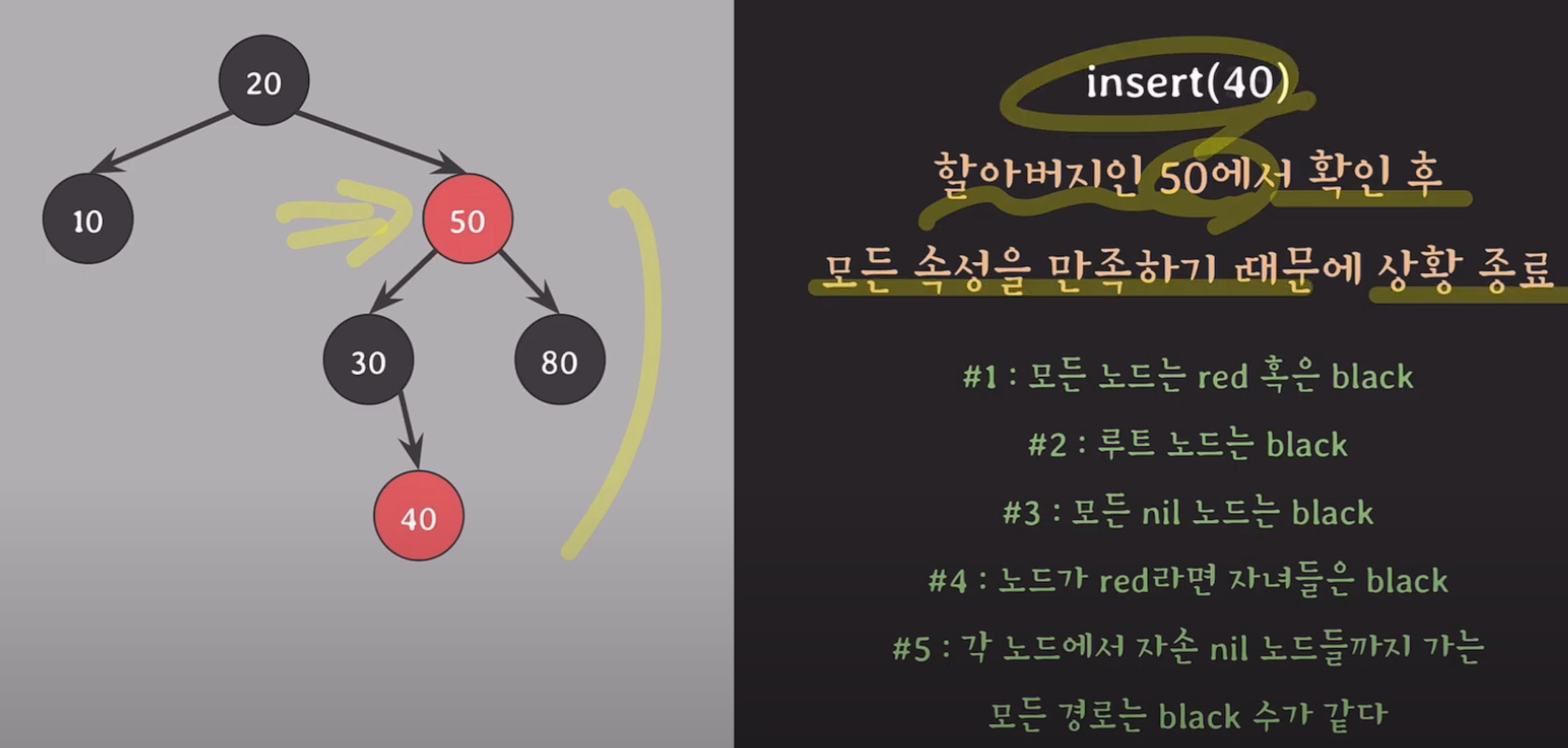
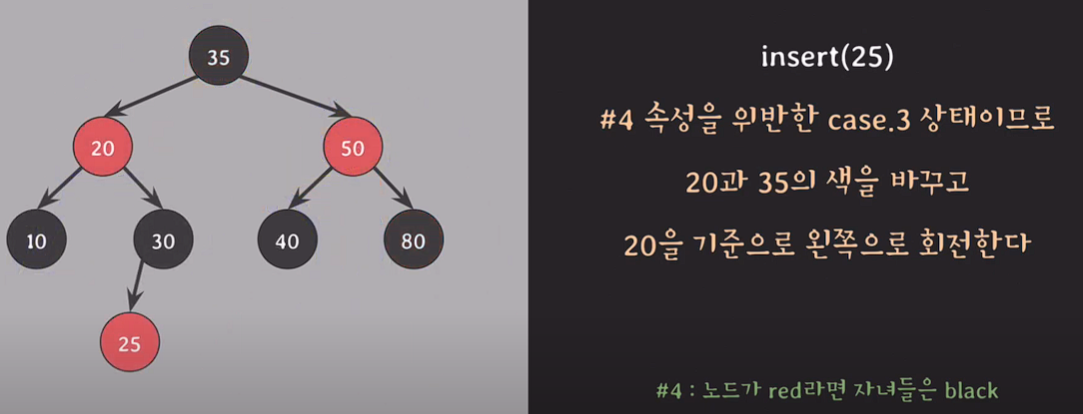
삭제

경우의 수 1 : 자녀가 없거나 자녀가 하나

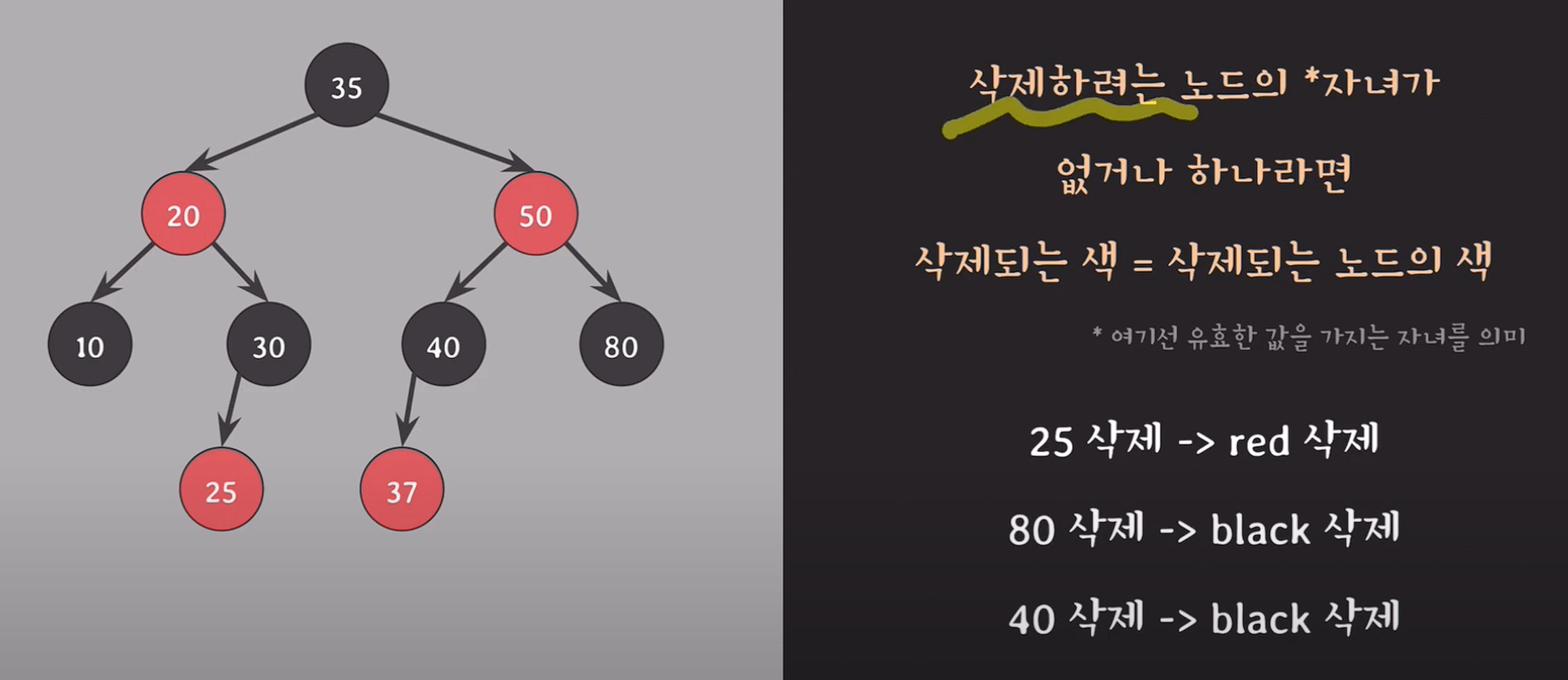
경우의 수 2 : 자녀가 둘

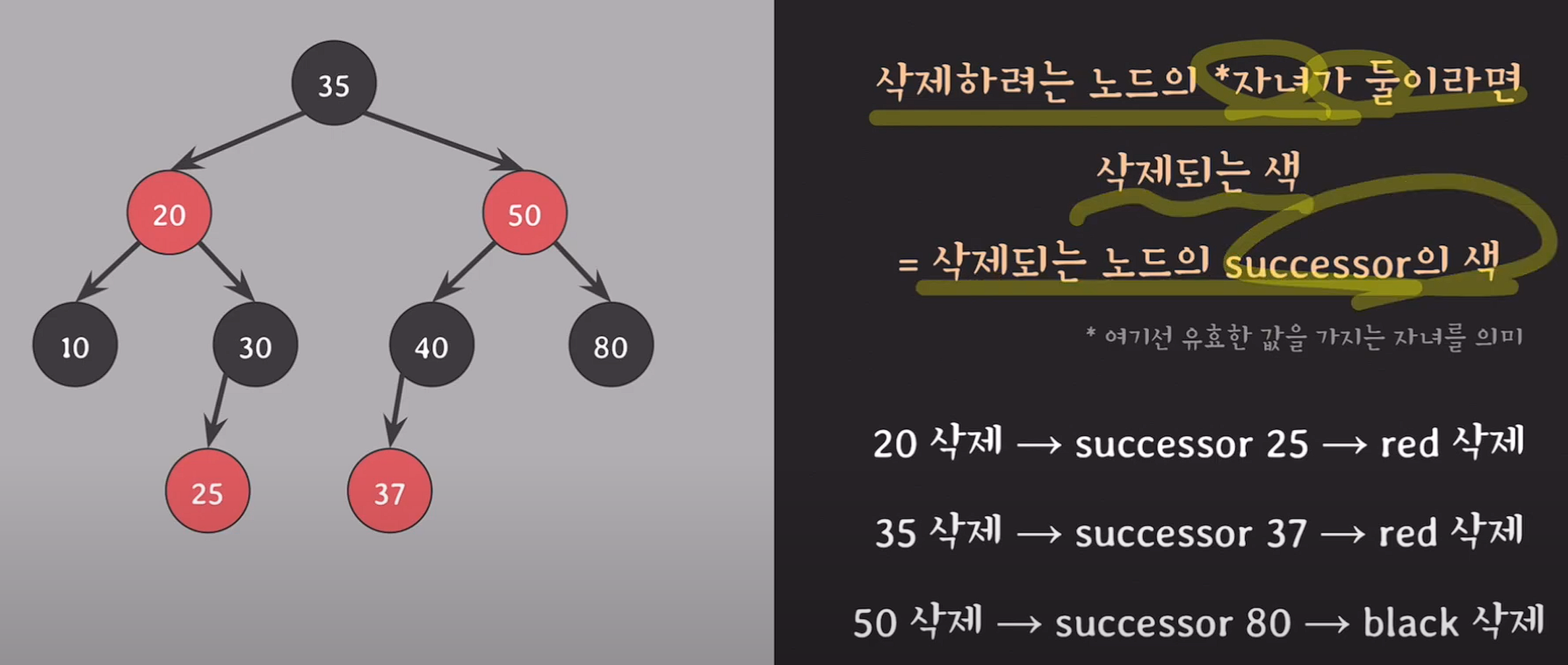
경우의 수 3 : 삭제되는 색이 red일때

경우의 수 4 : 삭제되는 색이 black일때

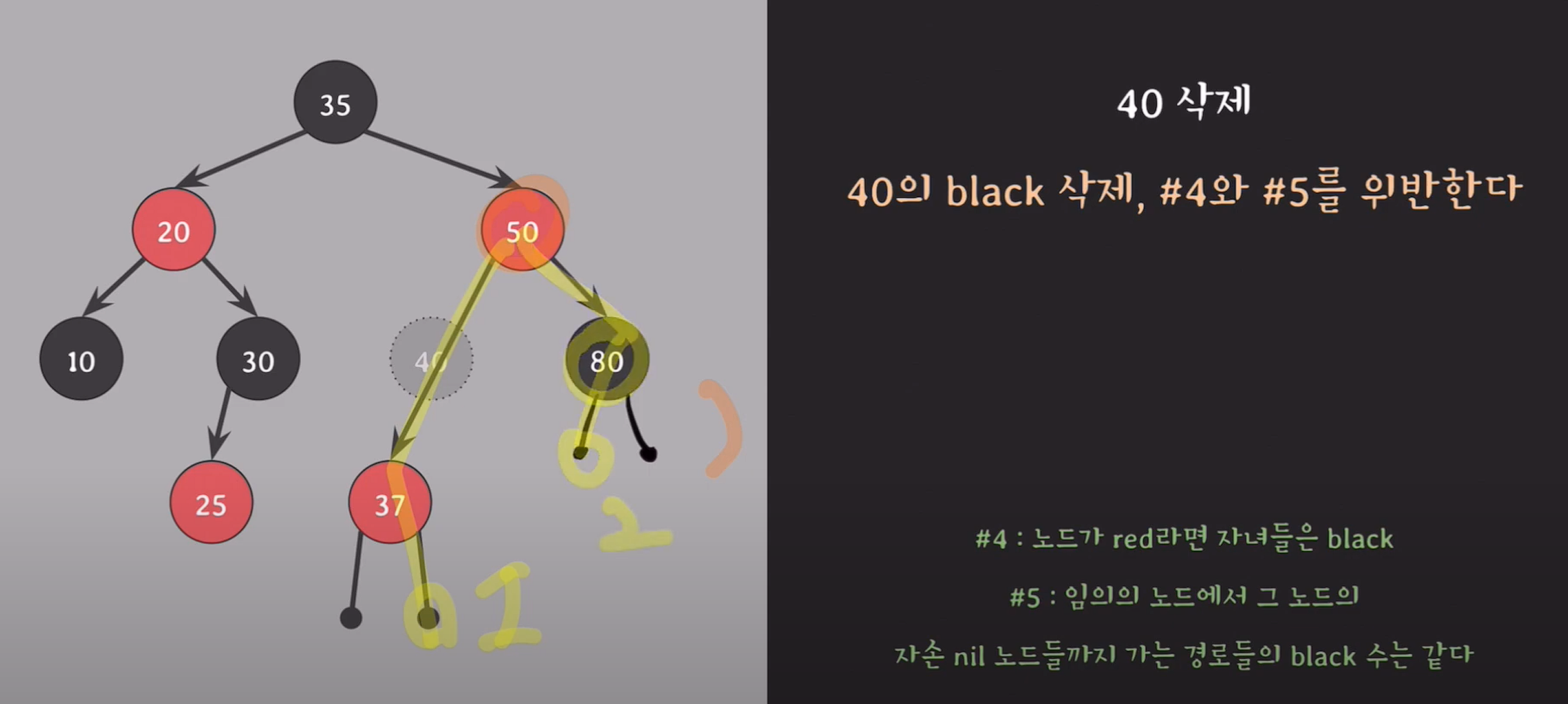
삭제 후 #5 위반

extra black

delete(10);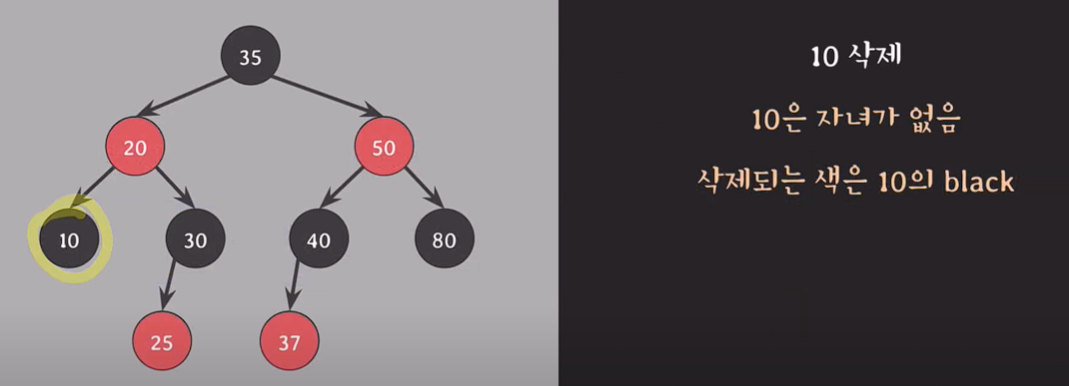

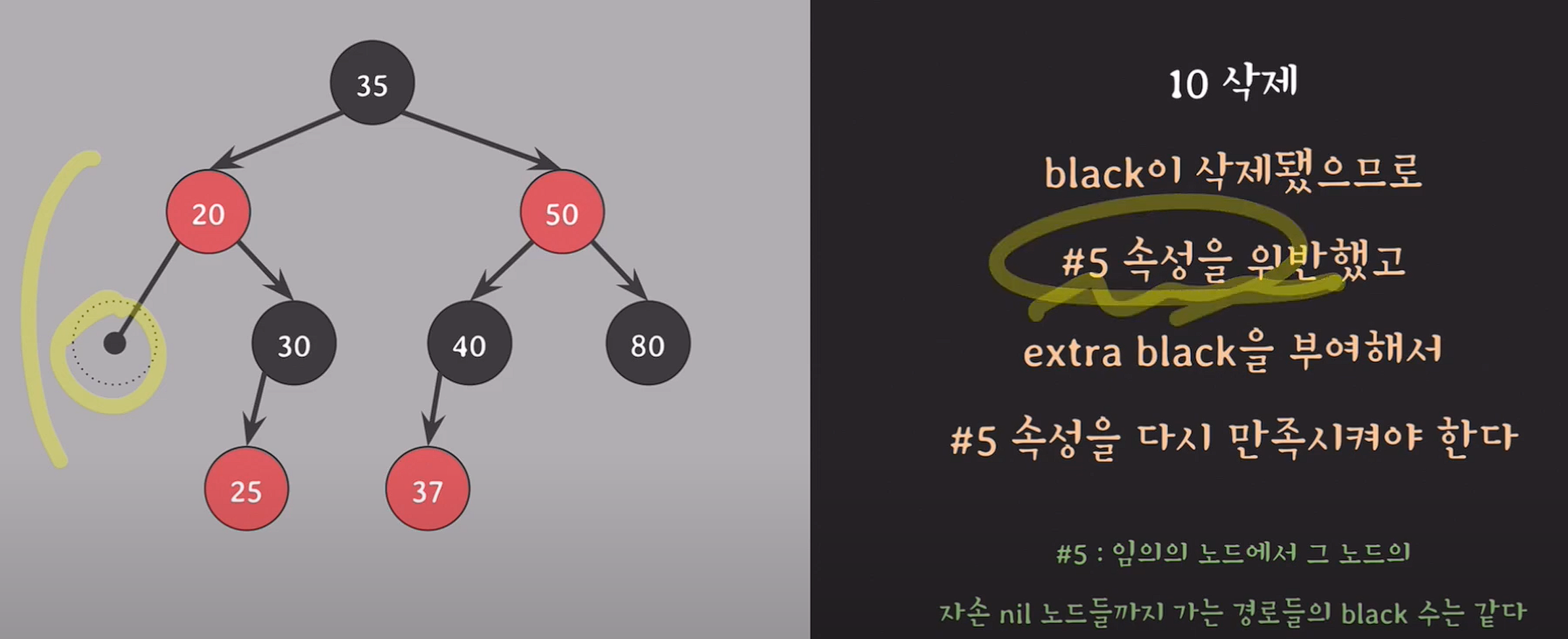
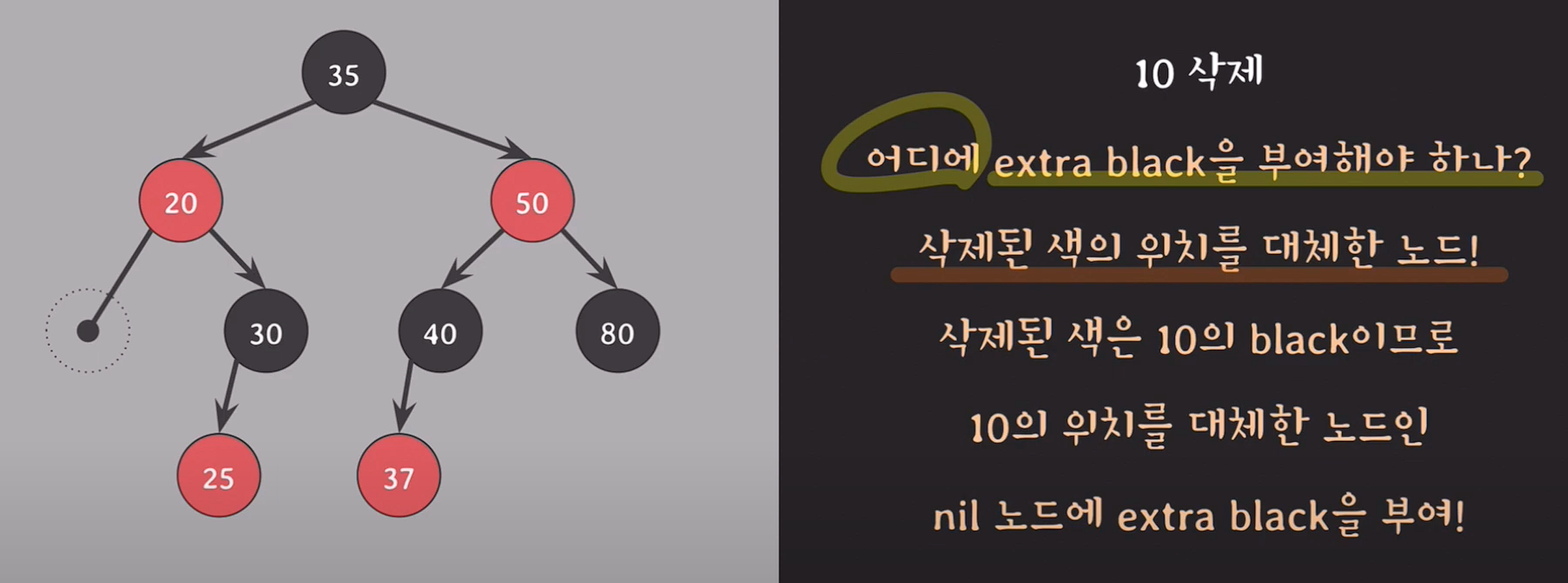
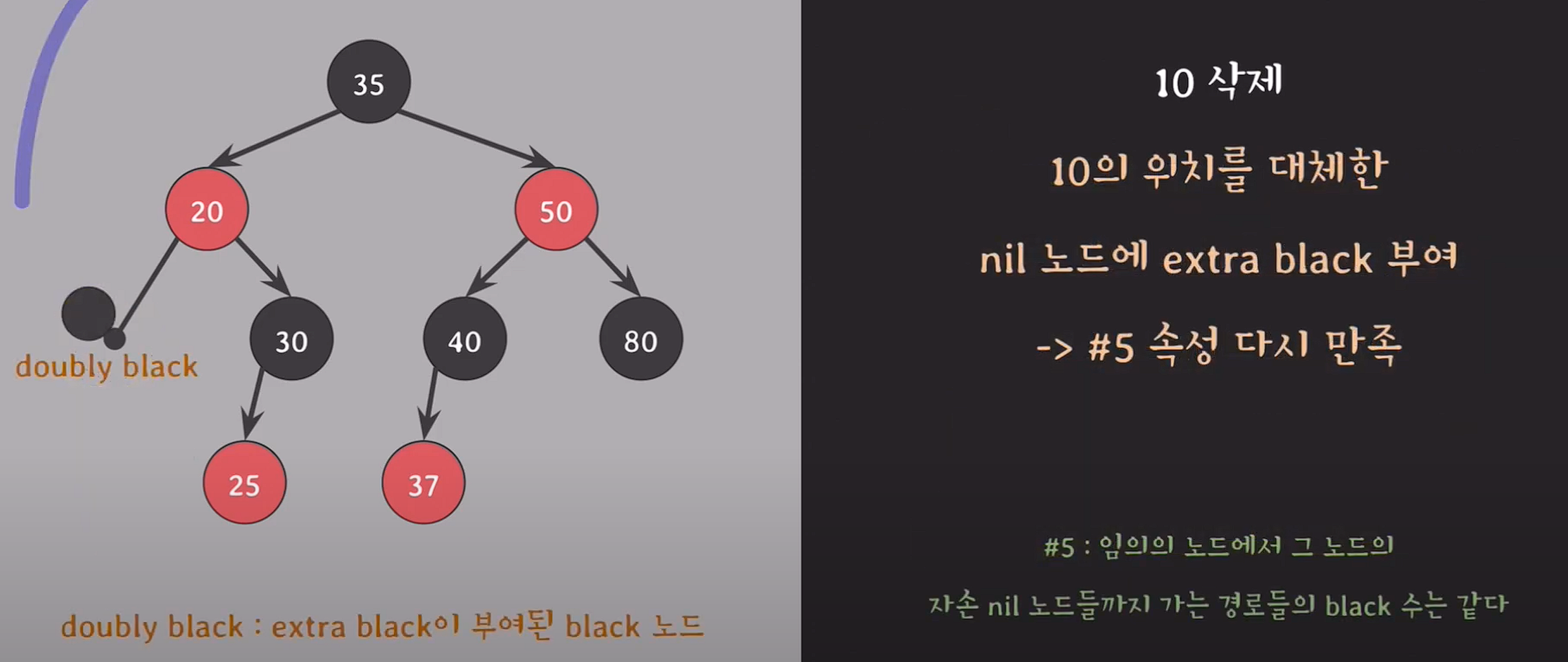
10은 자녀가 없기 때문에 black이 제거되고 #5를 맞추기 위해 10노드가 존재하던 위치에 extra black을 부여한다.

doubly black : extra black이 부여된 black노드

delete(30);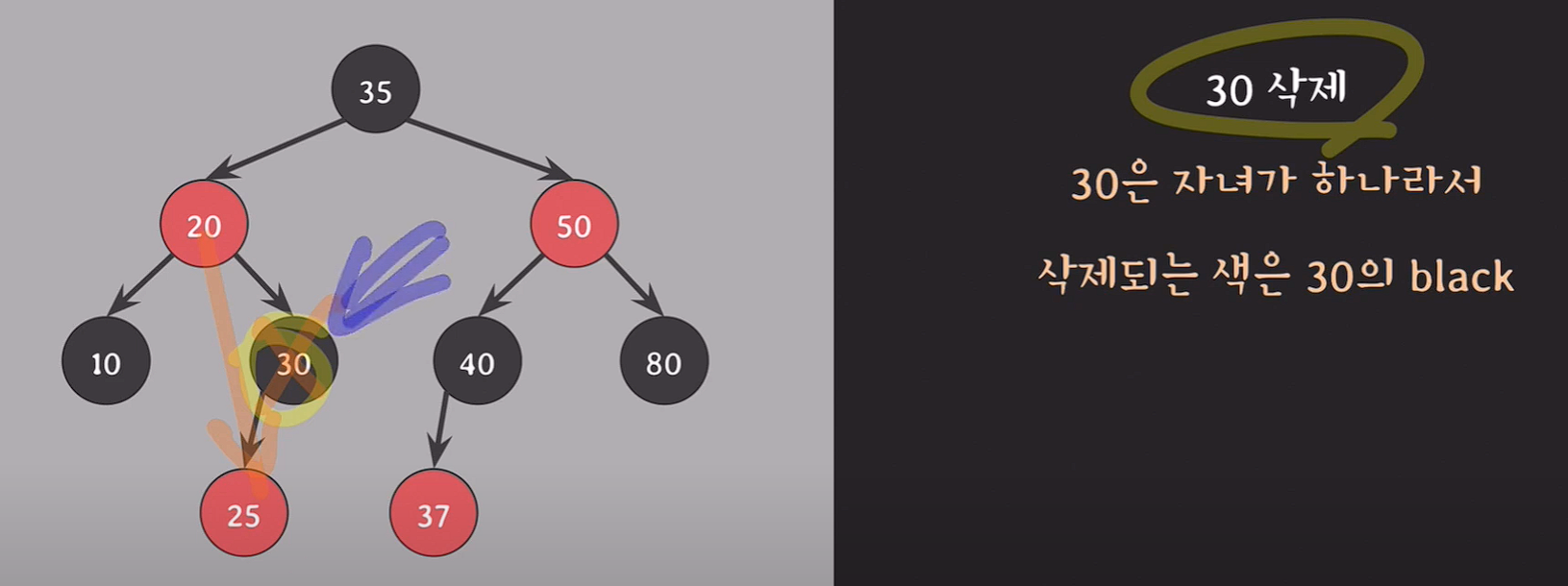

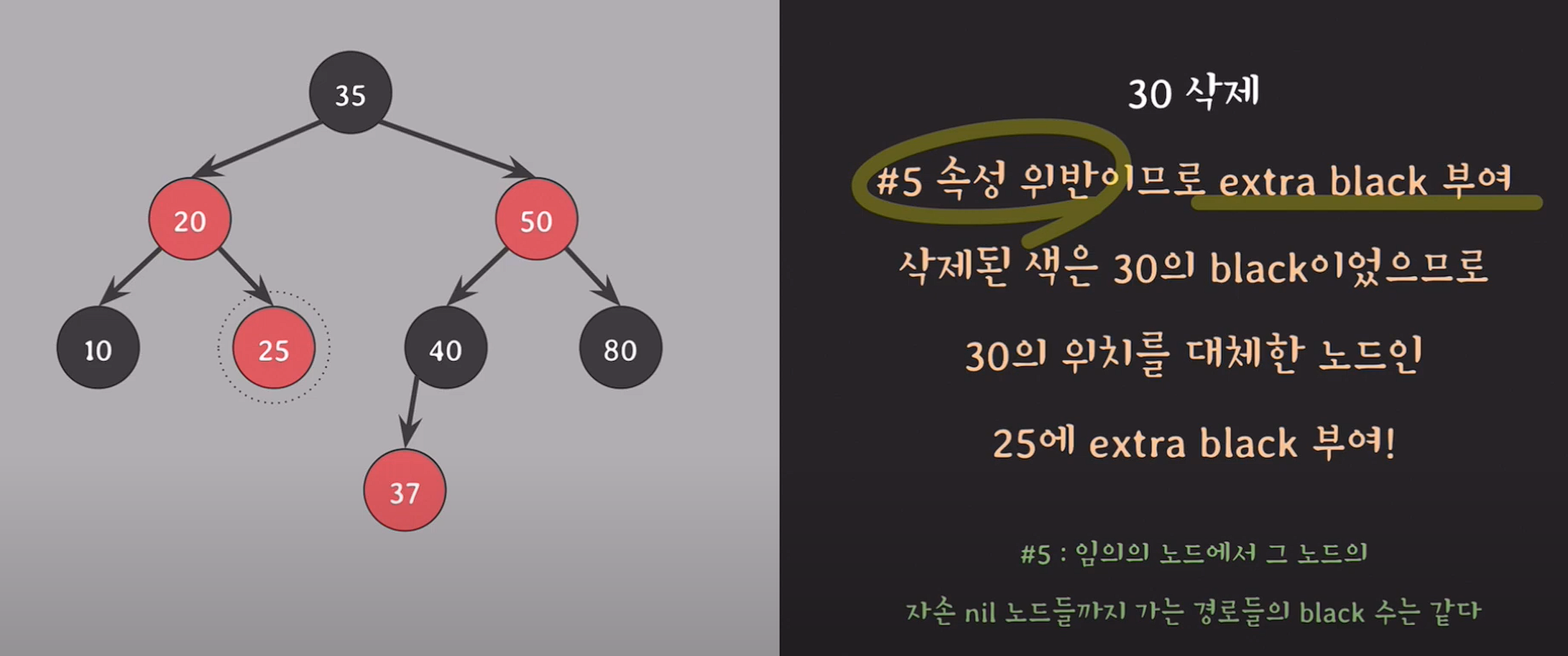
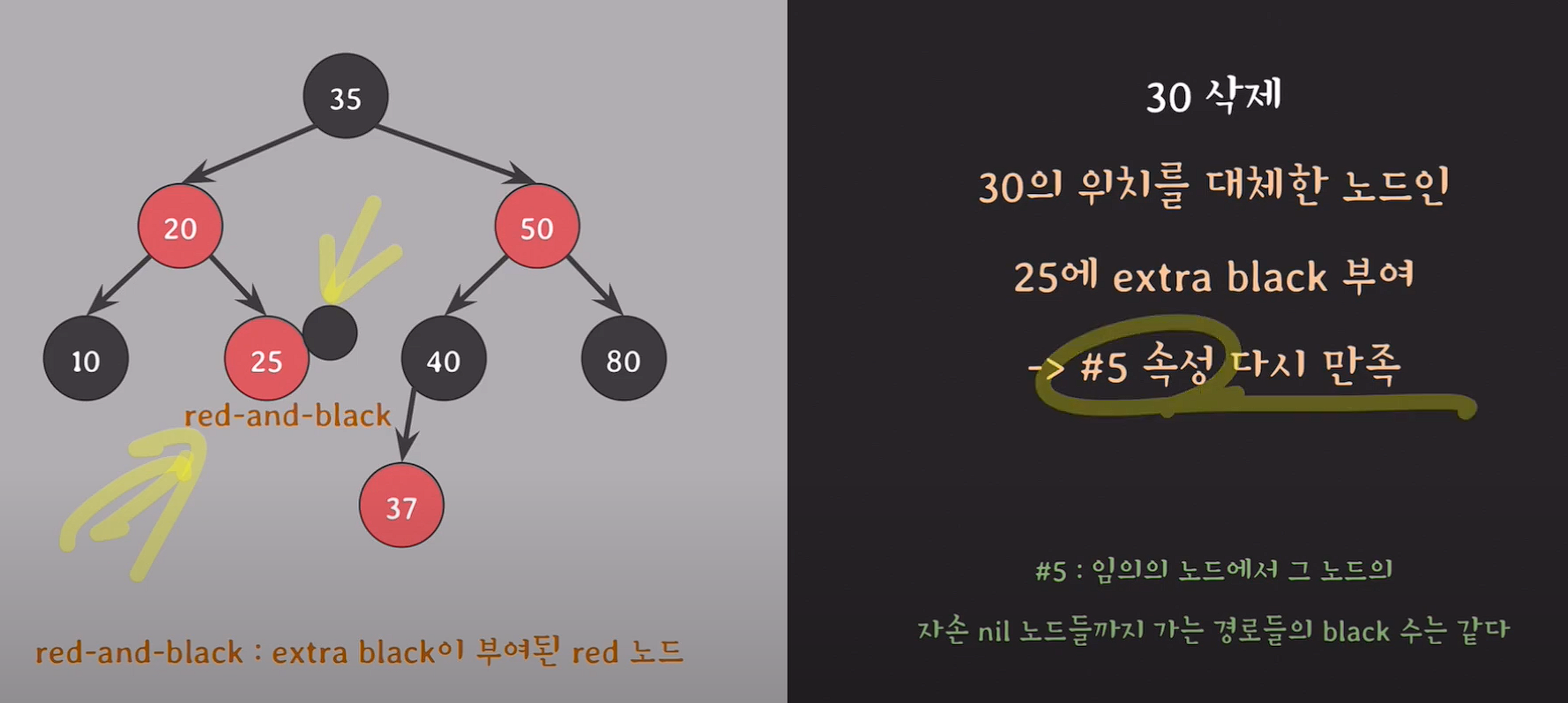
30은 자녀 노드가 1개이기 때문에, 삭제되는 색은 black이며 30의 자리를 대체하는 25에 extra black을 부여한다.

red-and-black : extra black이 부여된 red 노드

delete(50);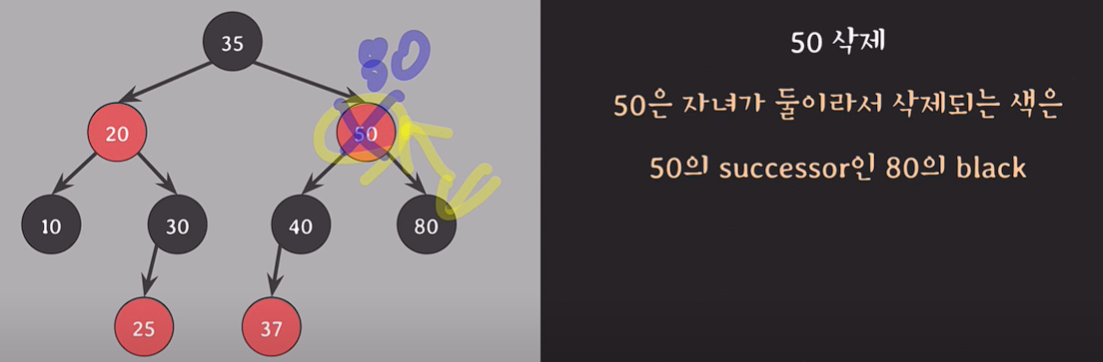

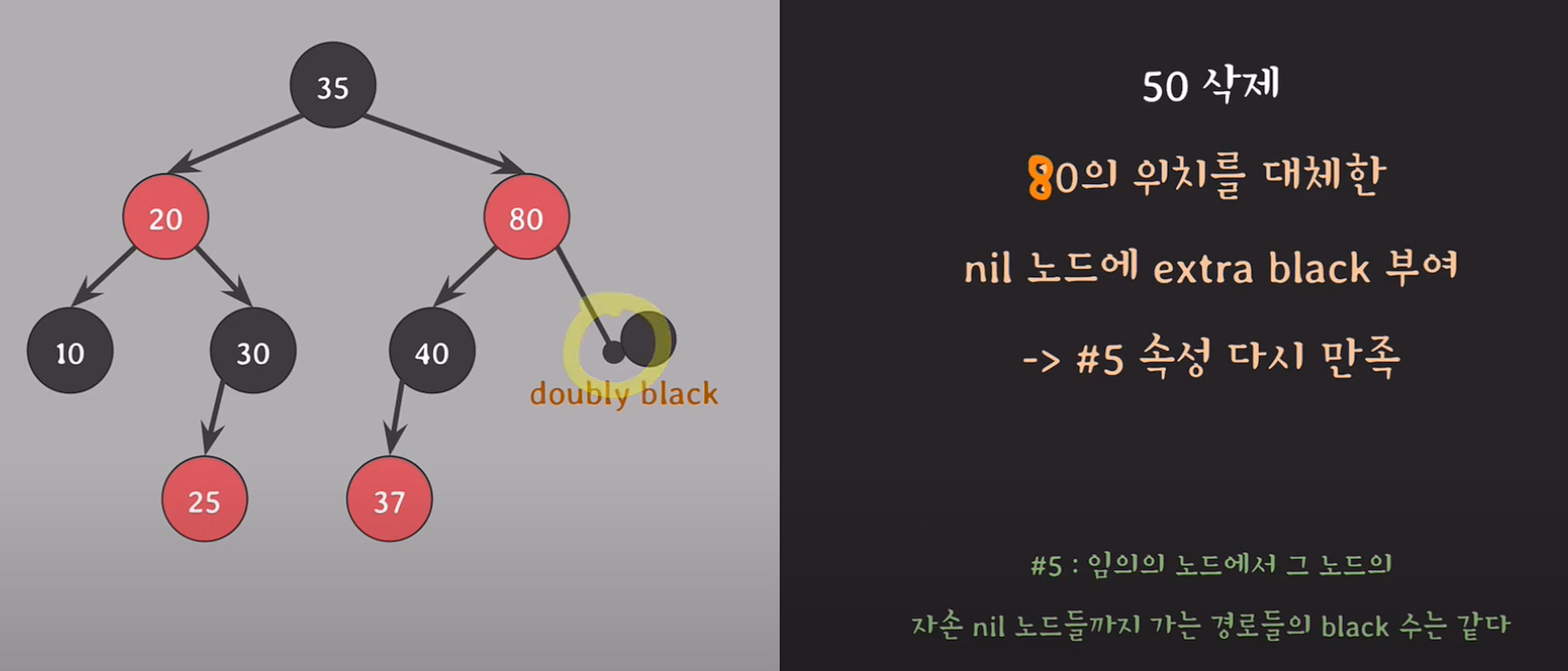
50은 자녀가 2개이기 때문에 successor의 색 black이 제거된다.

extra black이 부여된 노드 해결

red-and-black 노드

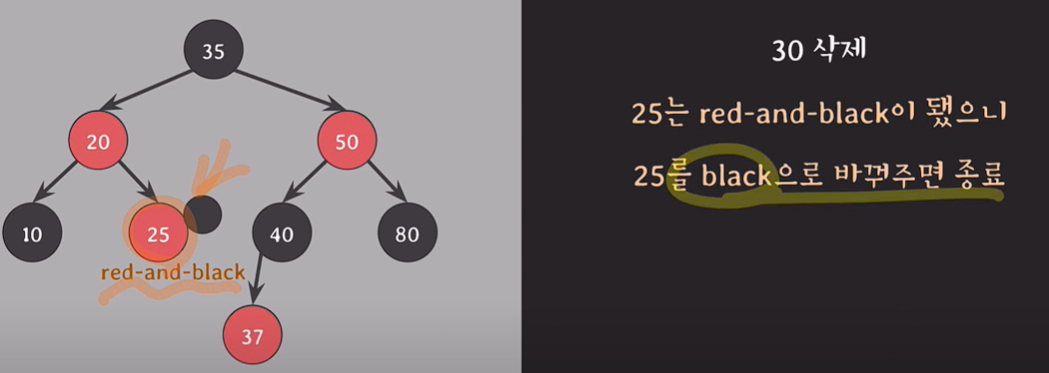
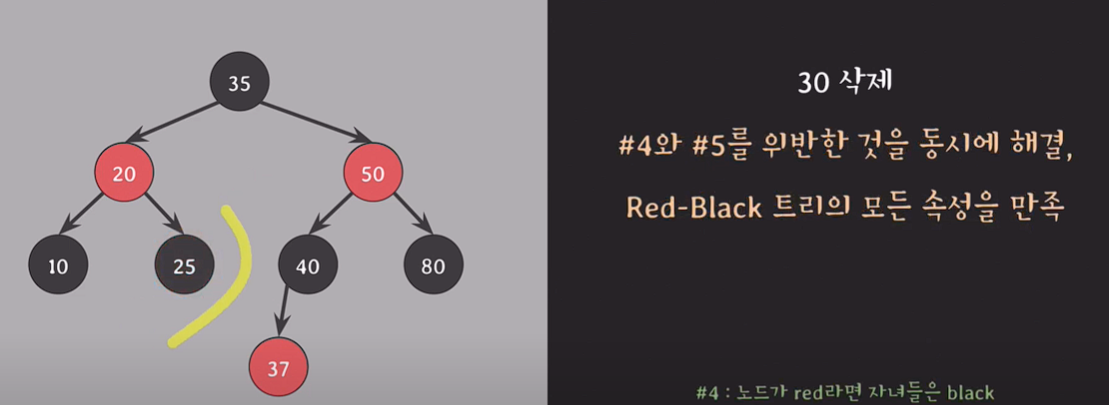
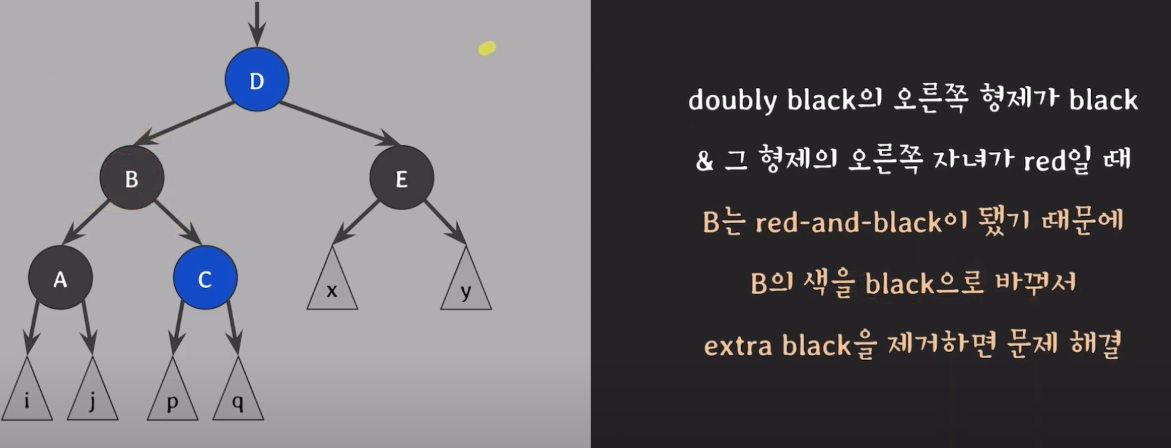
red-and-black 노드를 black으로 바꾸면 해결.

doubly black

결국 extra black을 어떻게 해결할 것인가 ? 4가지 방법이 존재한다.

doubly black의 형제의 색과 그 형제의 자녀들의 색에 따라 case가 나뉘어진다.

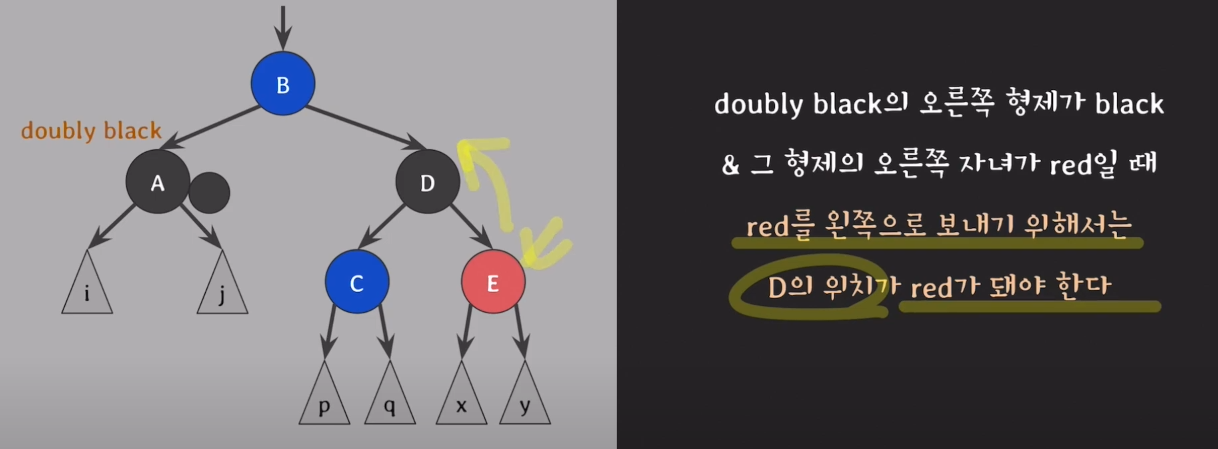
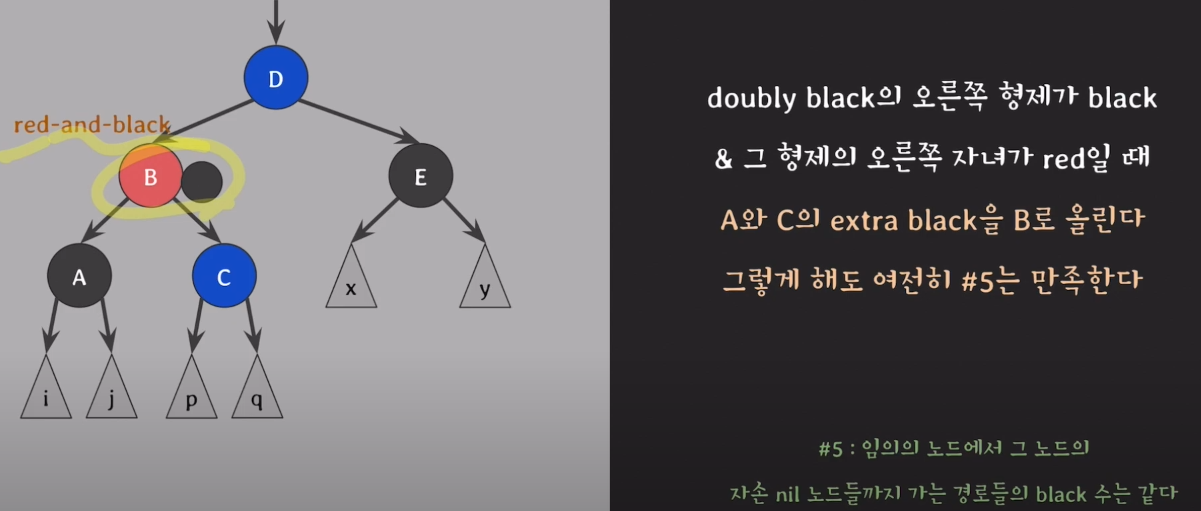
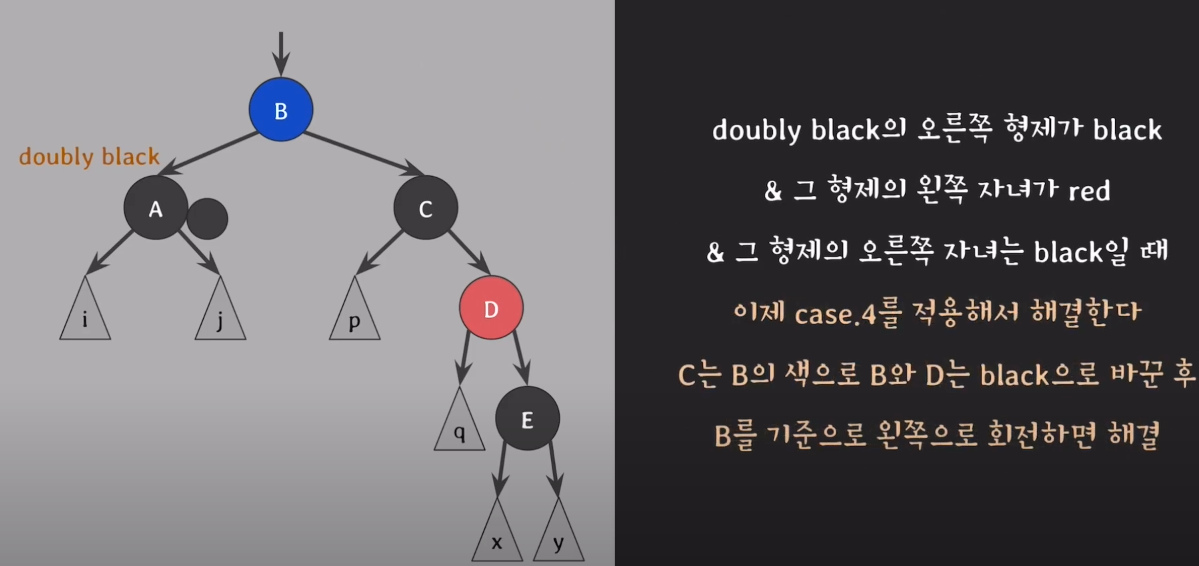
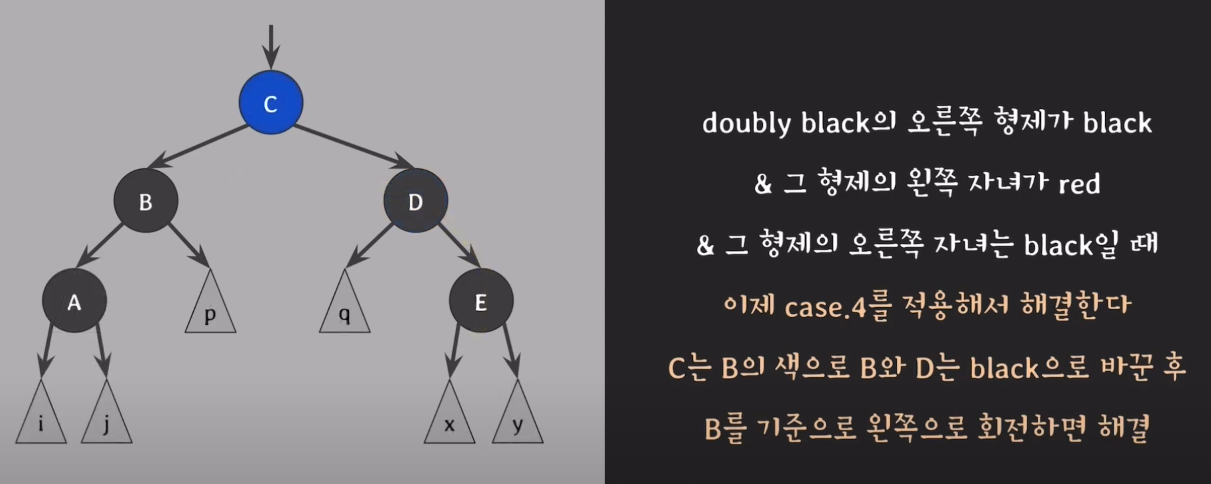
case4. doubly black의 오른쪽 형제가 black & 그 형제의 오른쪽 자녀가 red일때

파란색으로 표시한 노드는 어떤색이던지 상관없다.

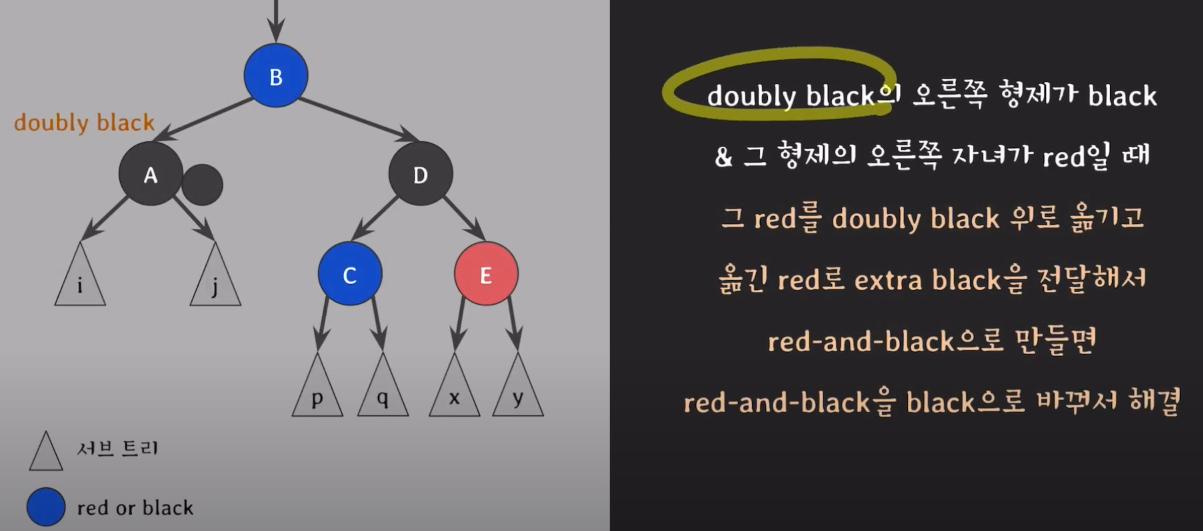
1)

레드 블랙 트리 특징 : 자녀의 노드색이 같을 경우 부모와 자녀색을 바꿔도 여전히 속성을 유지한다.

2) 부모의 자녀의 색 교환.

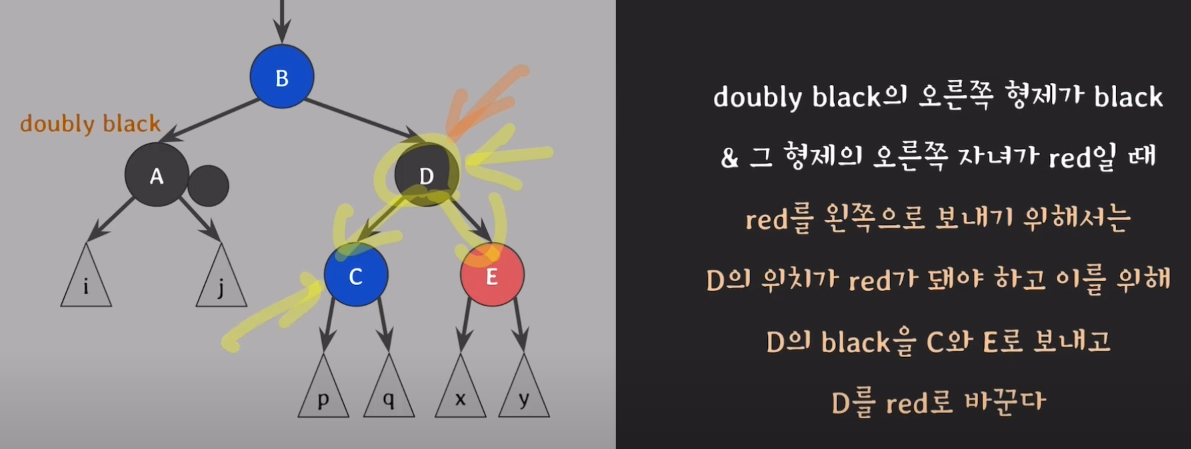
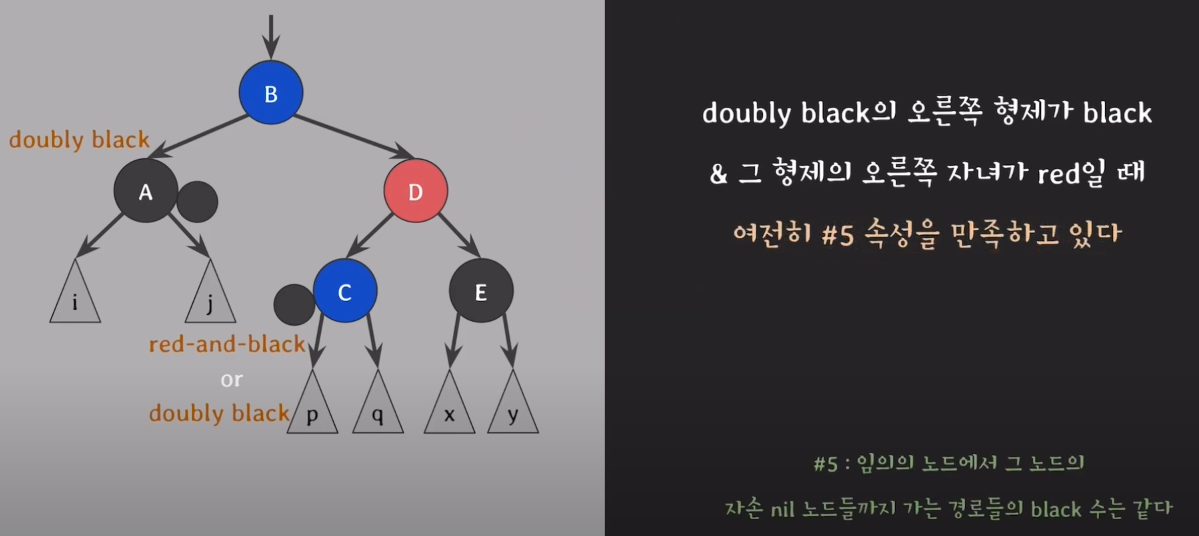
3) C의 색이 어떤것인지 모르기 때문에 red-and-black 또는 doubly black이 된다.

4) D가 왼쪽으로 갈 수 있도록 B와 D의 색을 바꾼다.

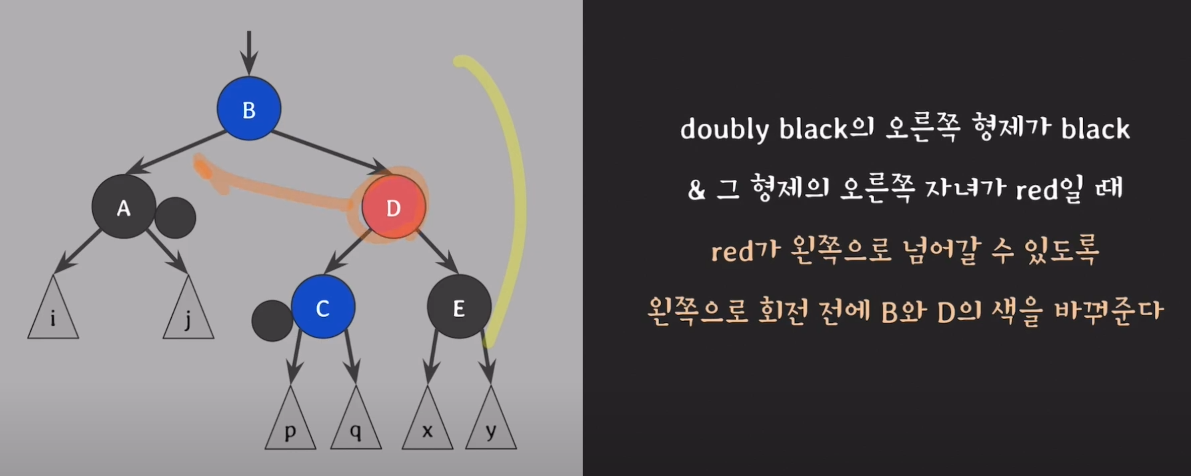
5) B를 기준으로 왼쪽으로 회전한다.

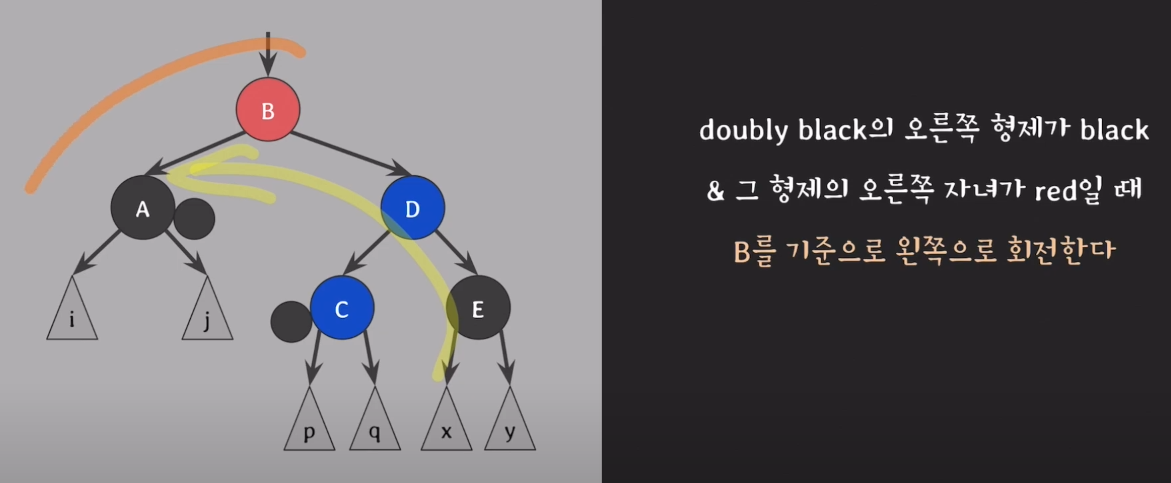
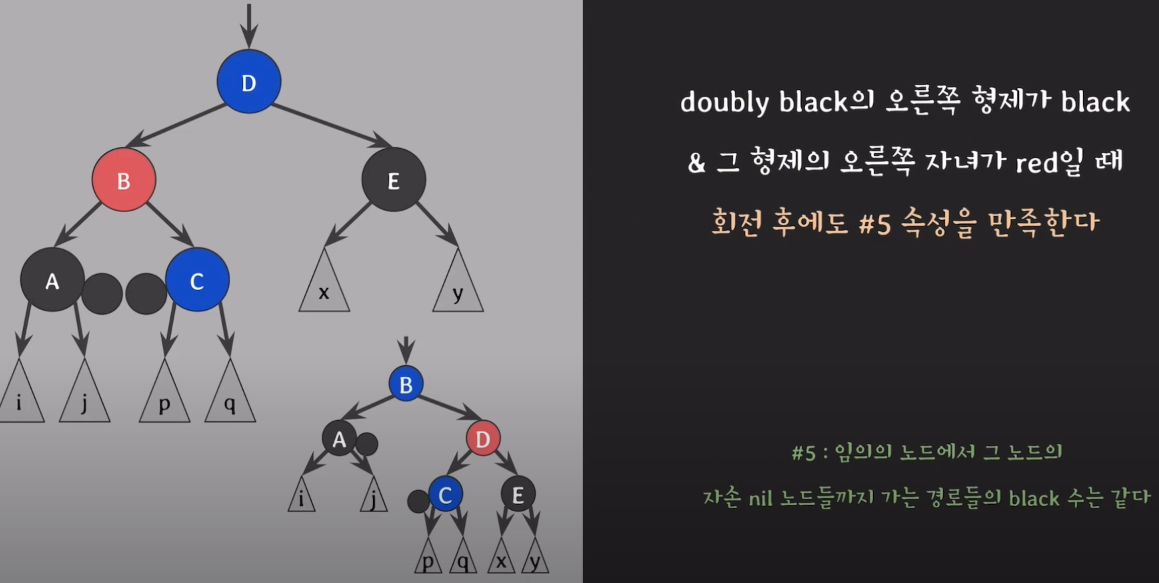
6) B의 자녀 노드 A,C는 extra black을 가지고 있는 상태이다.

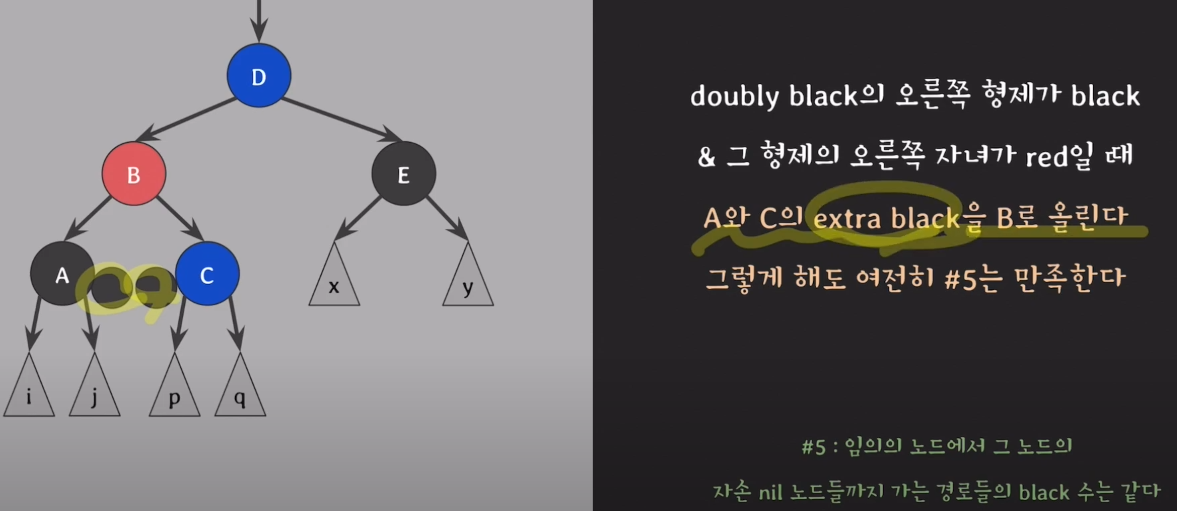
7) 자녀 노드에 존재하는 extra black을 부모 B로 보내고, B를 black으로 변경한다.

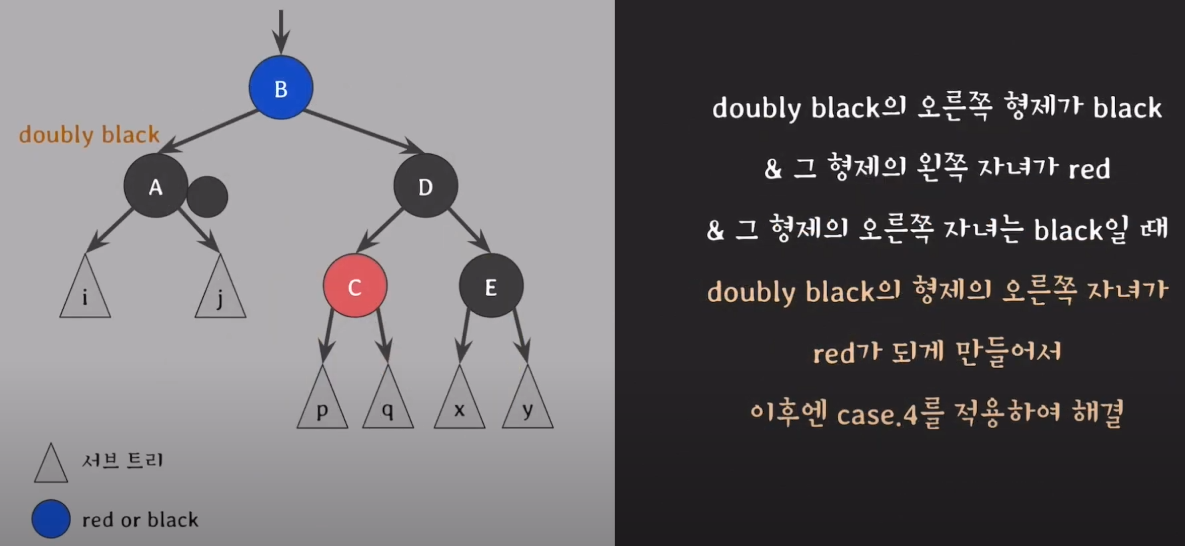
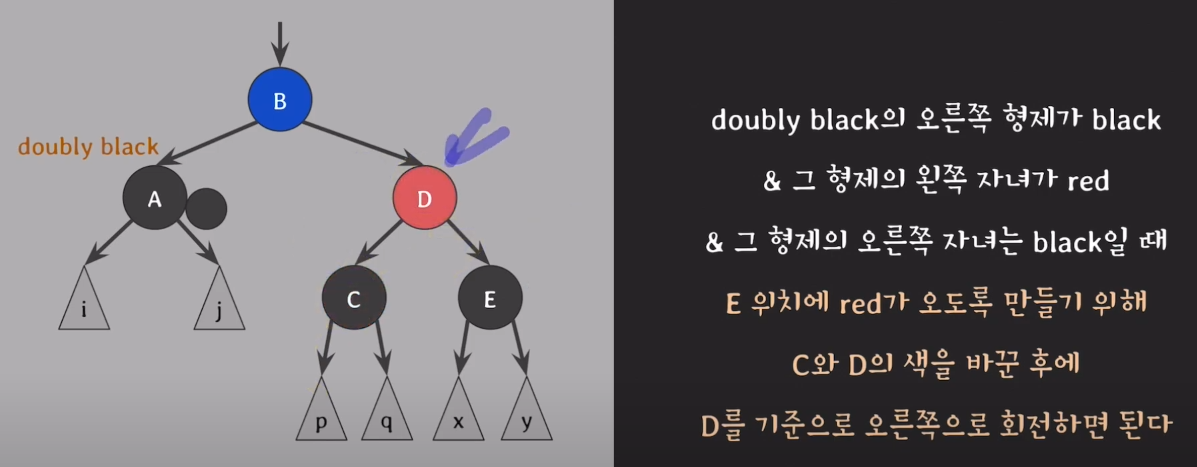
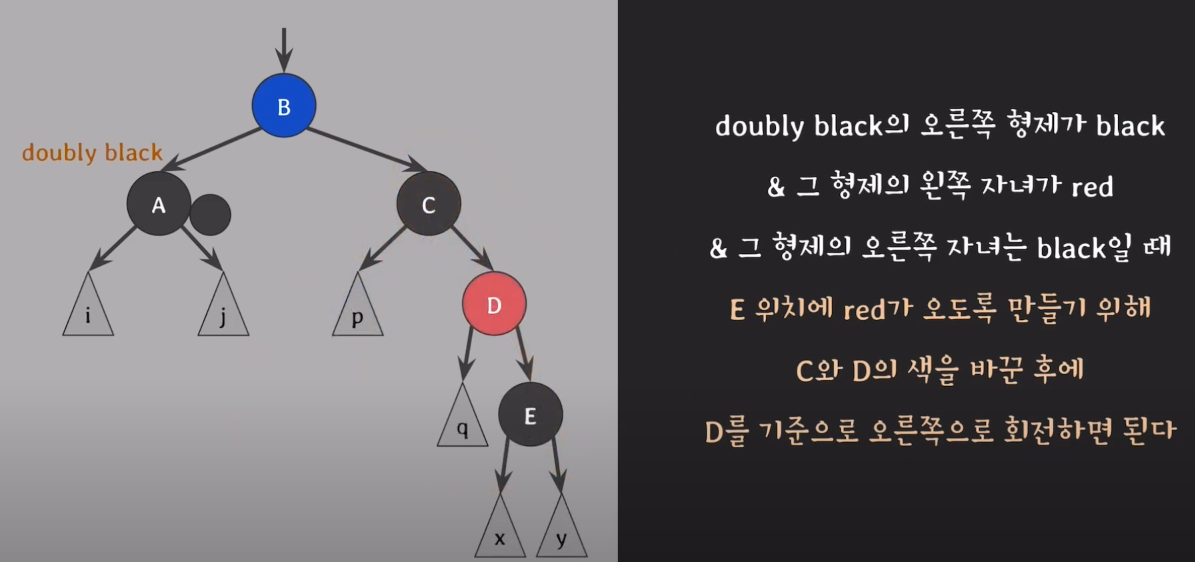
case3.doubly black의 오른쪽 형제가 black & 그 형제의 왼쪽 자녀가 red & 그 형제의 오른쪽 자녀는 black일 때

C의 red를 E로 옮기면 case4와 같은형태이다. 즉, C의 red를 E로 옮기고 case4처럼 진행한다.

1. E위치에 red가 오도록 만들기 위해 C와 D의 색을 바꾼다.

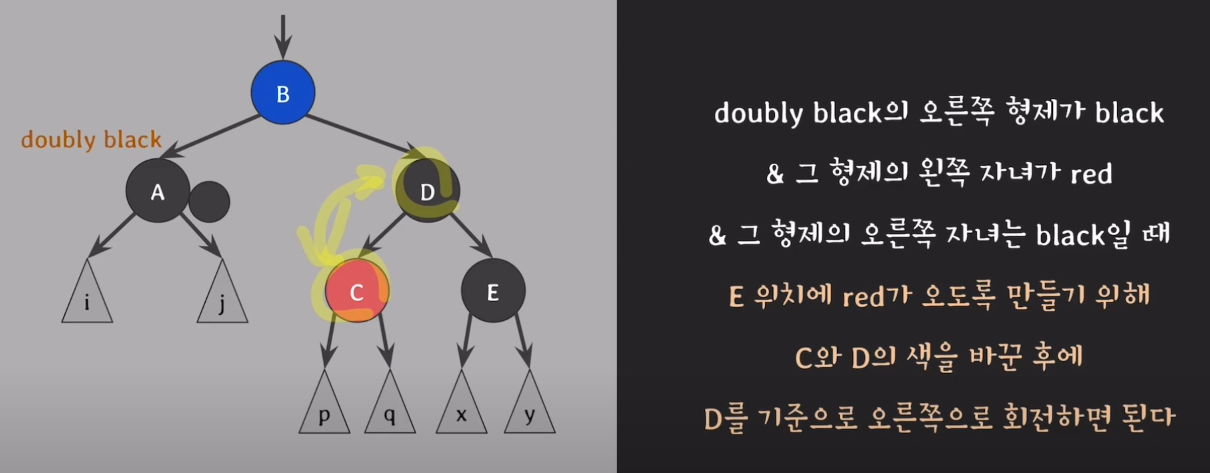
2. D를 기준으로 오른쪽으로 회전한다.

case2. doubly black의 형제가 black & 그 형제의 두자녀 모두 black일때

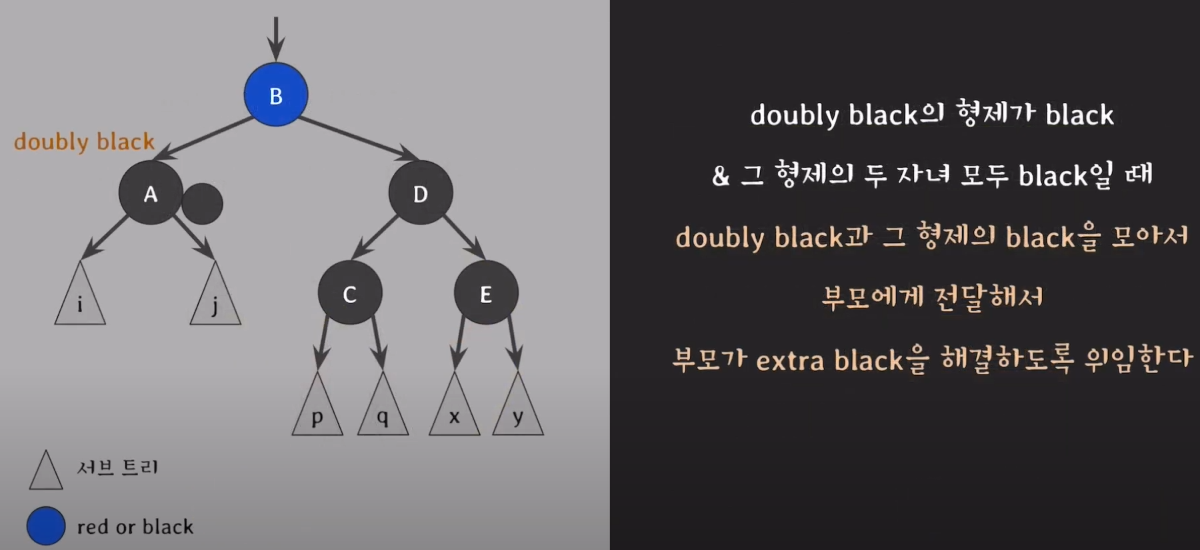
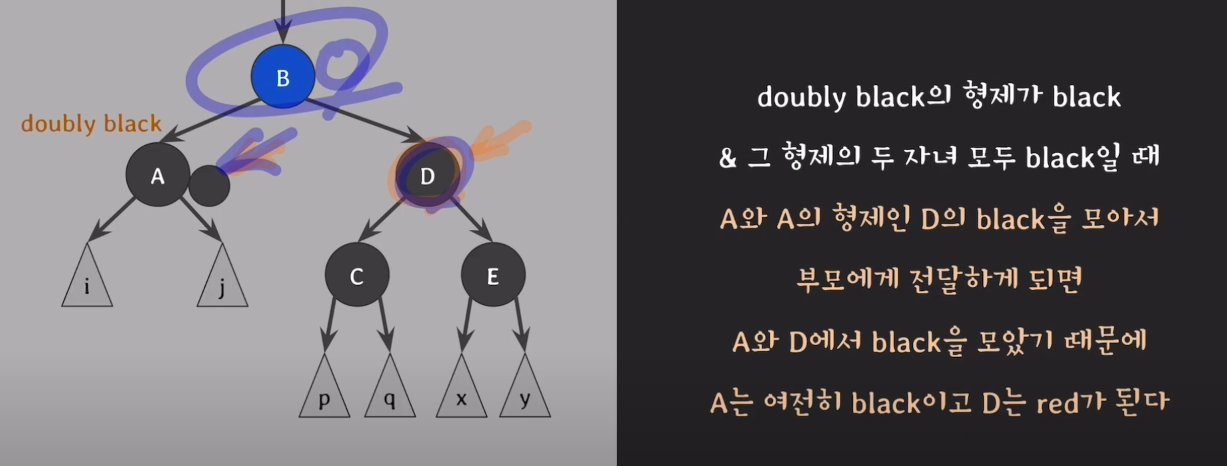
1. A의 extra black과 D의 black을 부모 노드에 위임한다.

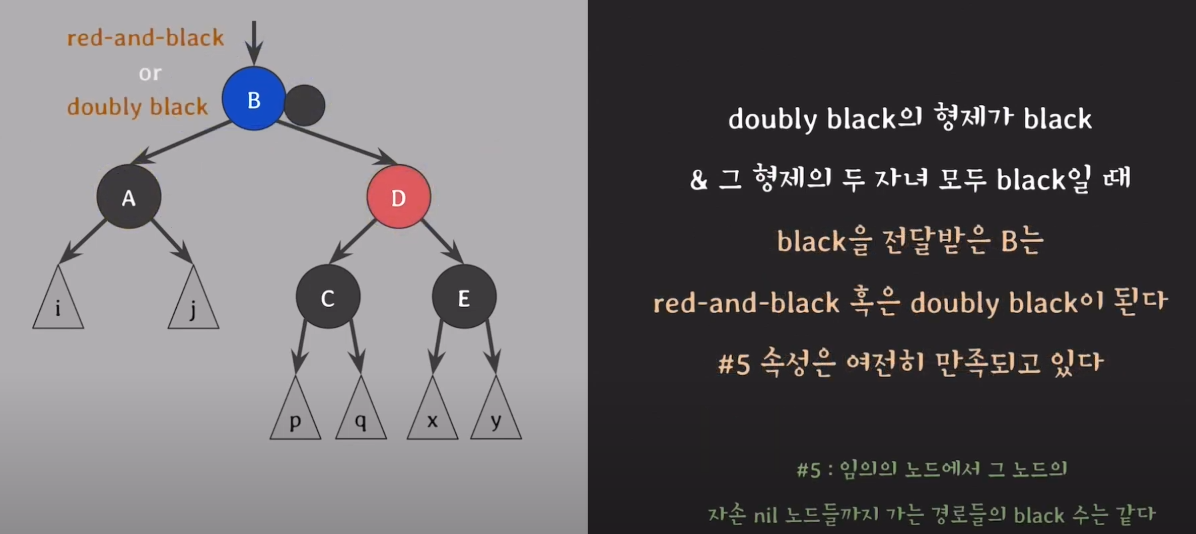
2. B가 red-and-black일 경우 black으로 바꾸면 되고, doubly black이면 case1,2,3,4로 해결한다.

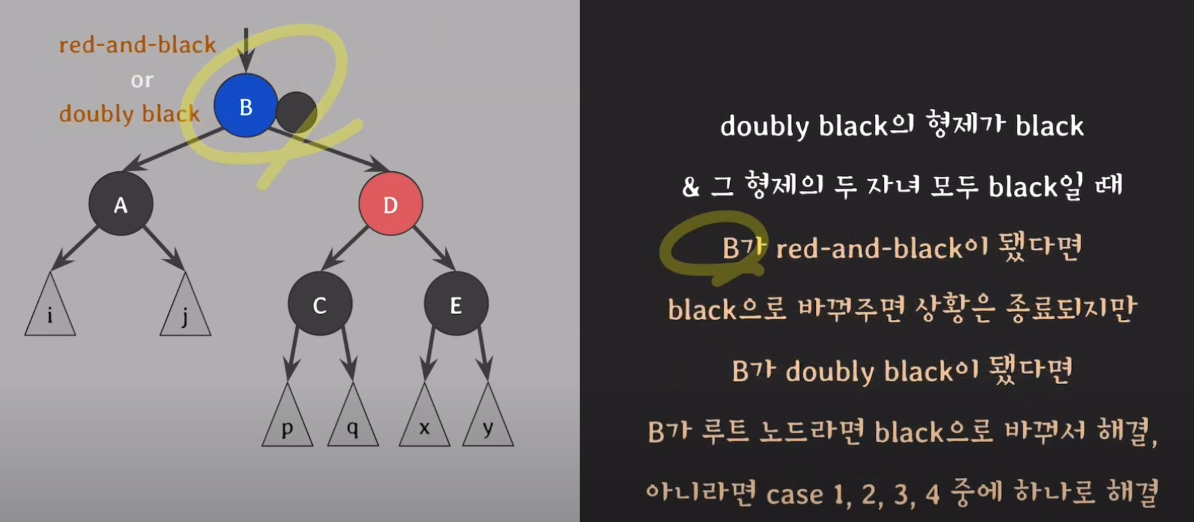
case1.doubly black의 형제가 red 일때

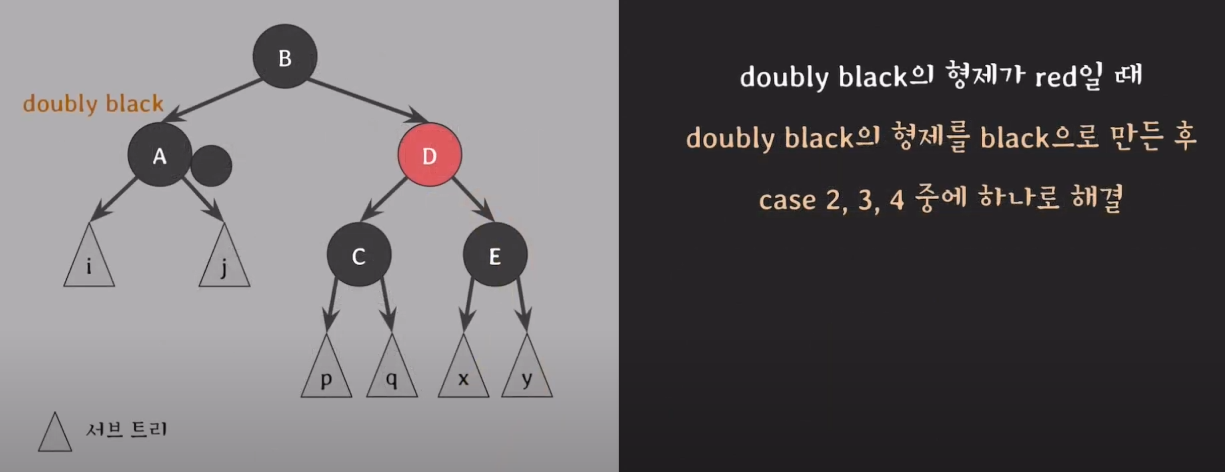
1. B를 기준으로 왼쪽으로 회전한다.

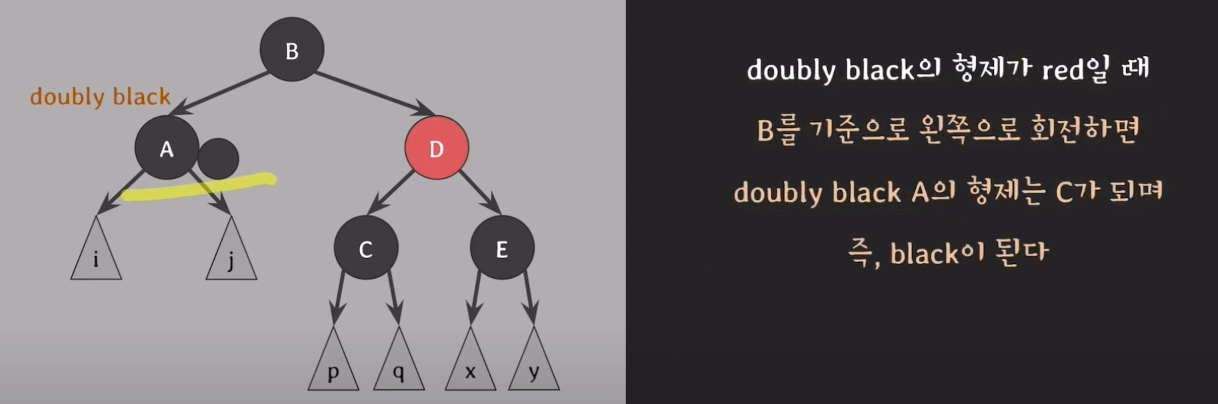
2. B와 D의 색을 변경한다.

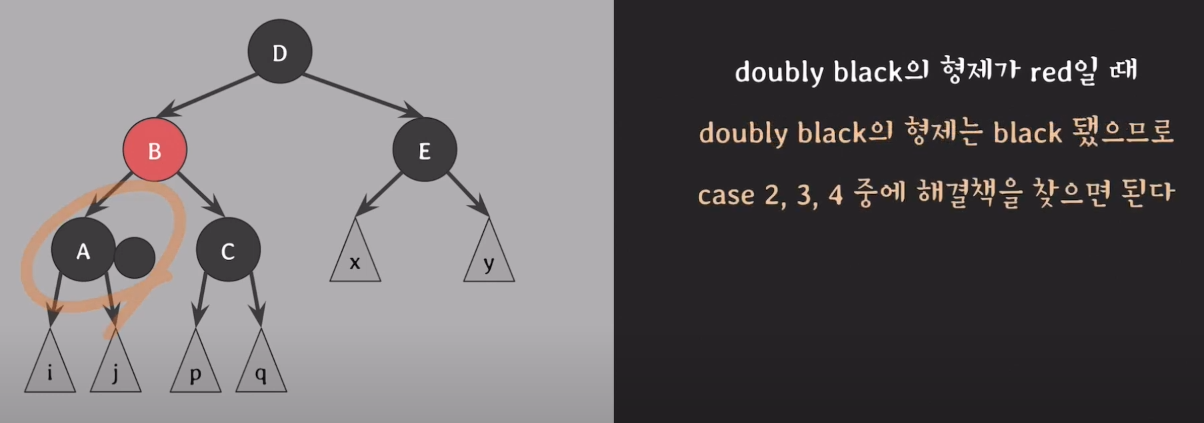
삭제되는 색이 black일때 정리

유튜브 26:58 red-black-tree 삭제 예제(이해하기!)

시간복잡도

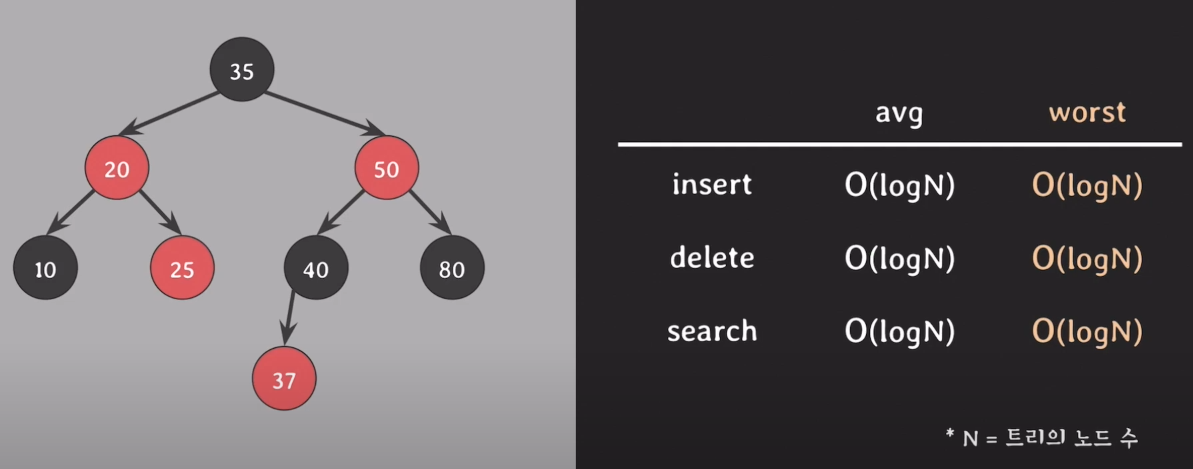
O(logN)

AVL 트리와 비교

출처 : 쉬운코드 유튜브