Binary Search Tree

기본개념
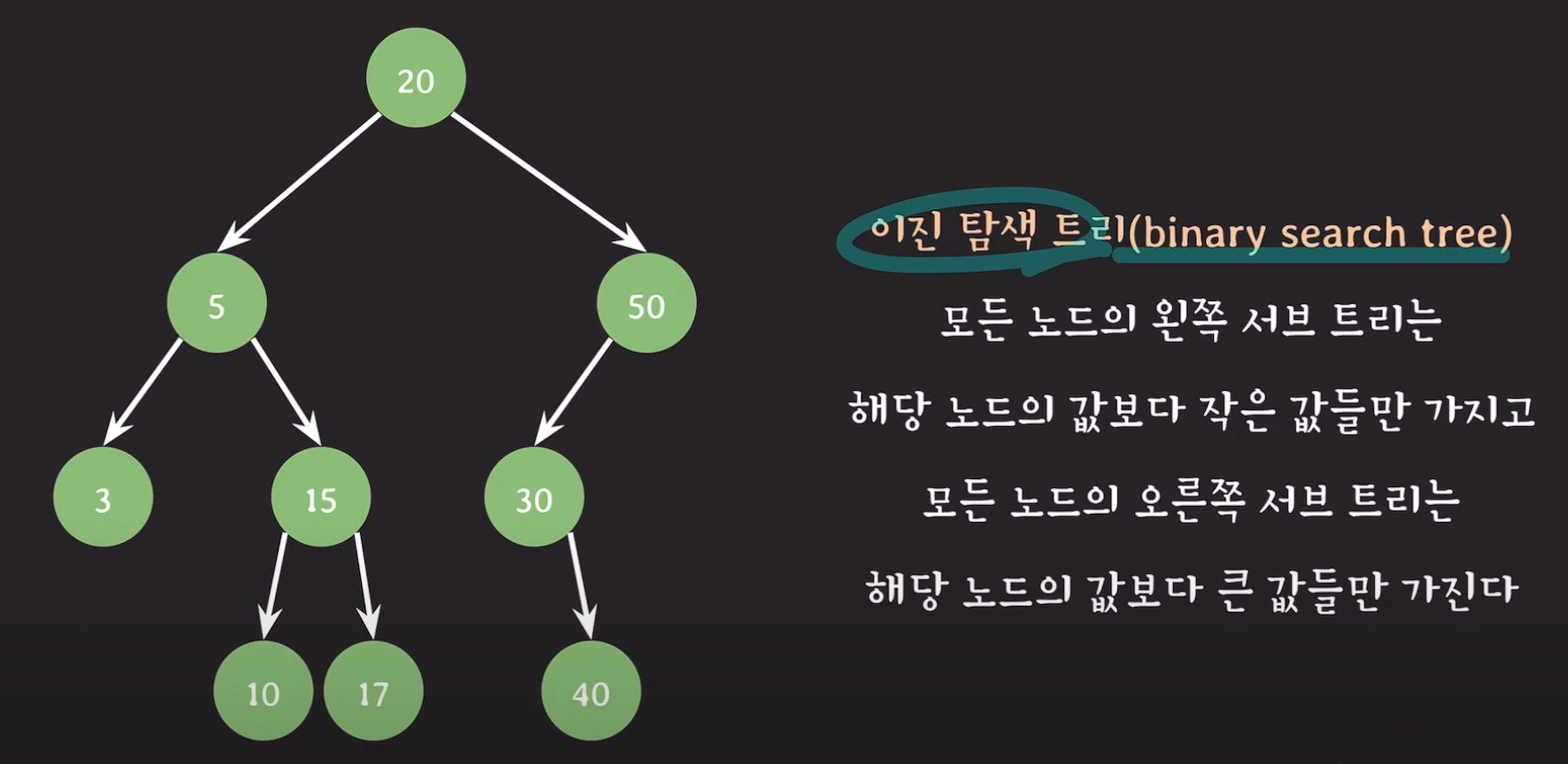
모든 노드의 왼쪽 서브 트리는 해당 노드의 값보다 작은 값들만 가지고 모든 노드의 오른쪽 서브 트리는 해당 노드의 값도가 큰 값들만 가진다.
ex) root node를 기준으로 오른쪽 서브트리의 모든 노드들은 20보다 크지만,
왼쪽 서브트리의 노드들은 20보다 작다.
==> ★모든 서브트리를 기준으로도 해당 규칙이 적용된다.
최소값
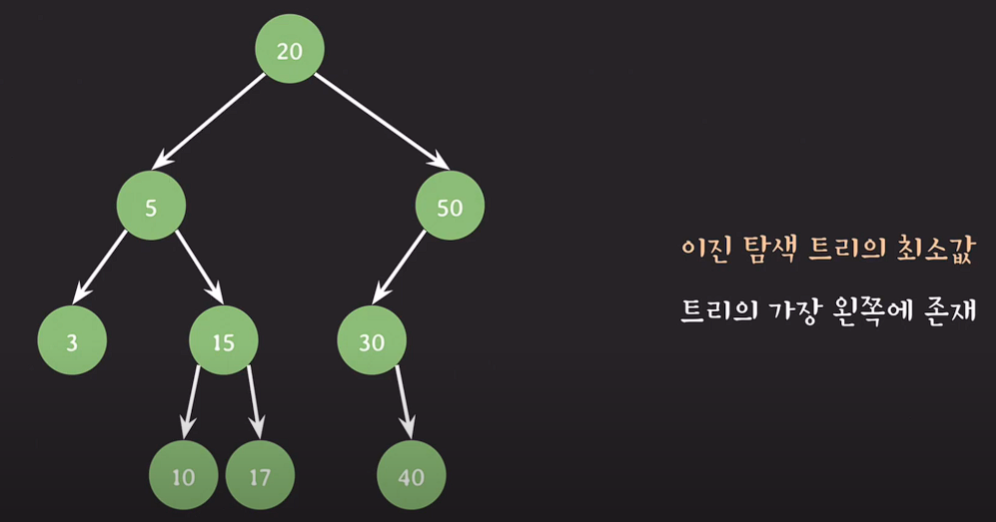
이진 탐색 트리의 최소값은 트리의 가장 왼쪽에 존재한다.
ex) 3 ==> 더이상 왼쪽 서브트리가 존재하지 않는다.
최대값
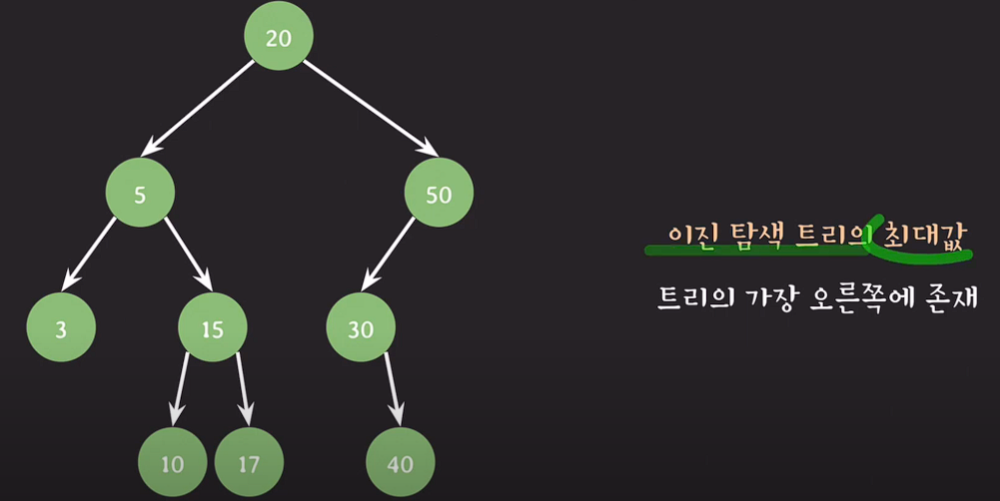
이진 탐색 트리의 최대값은 트리의 가장 오른쪽에 존재한다.
ex) 50 ==> 더이상 오른쪽 서브트리가 존재하지 않는다.
후임자(successor)
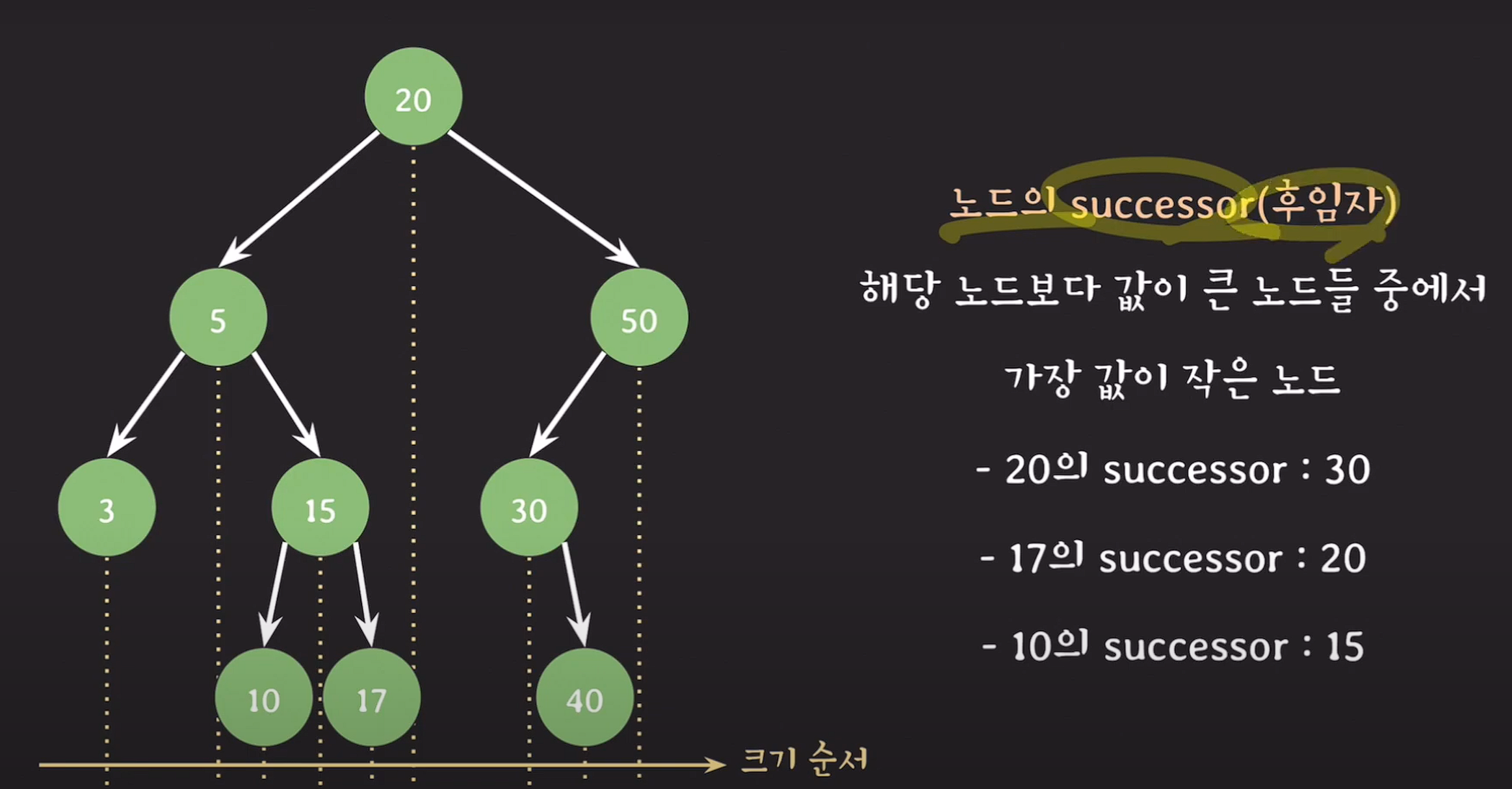
해당 노드보다 값이 큰 노드들 중에서 가장 값이 작은 노드
ex) 해당 노드의 수직선을 기준으로 바로 오른쪽 노드
선임자(predecessor)
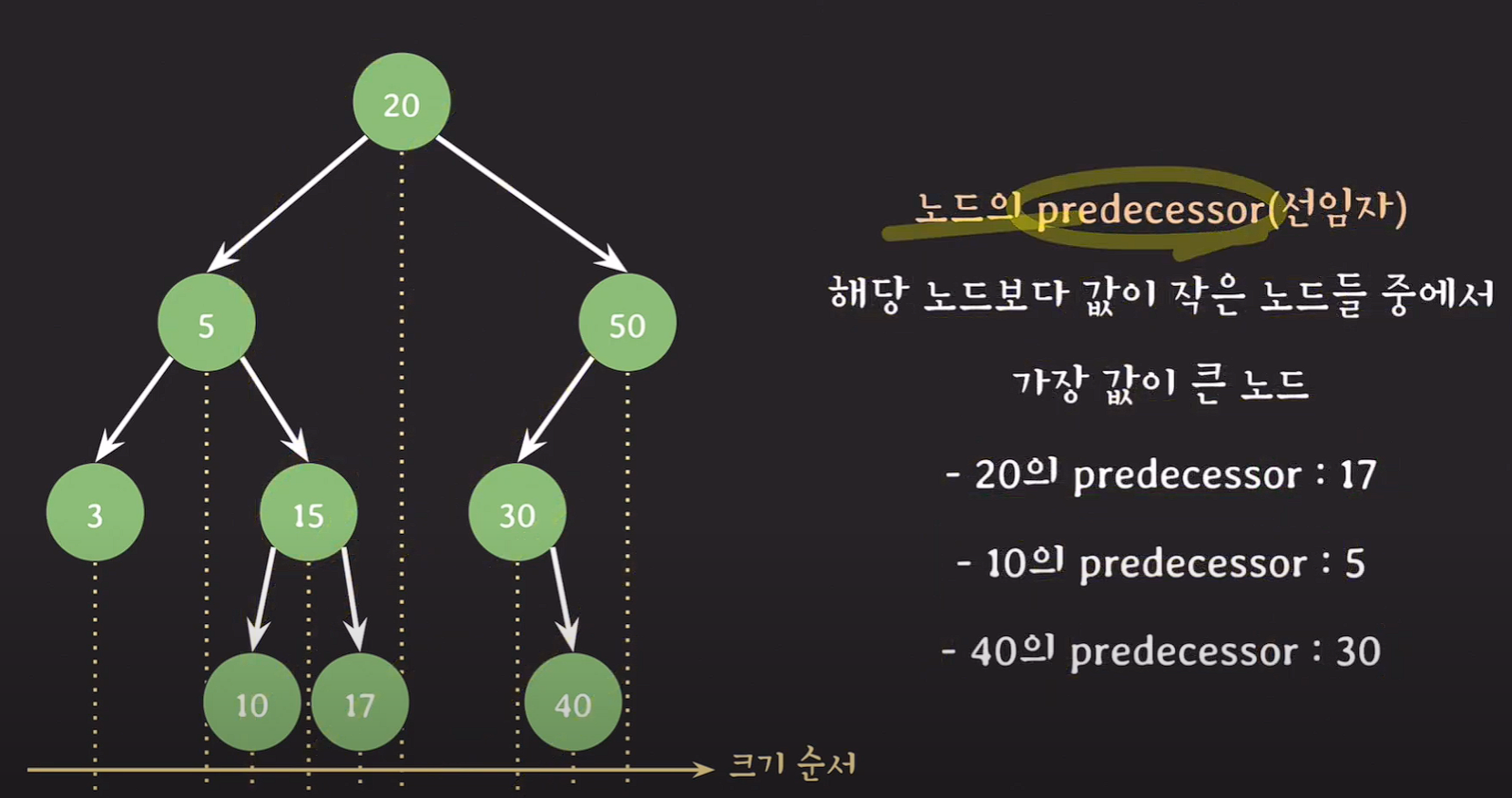
해당 노드보다 값이 작은 노드들 중에서 가장 값이 큰 노드
ex) 해당 노드의 수직선을 기준으로 바로 왼쪽 노드
순회 방법
순회란, BST에 존재하는 모든 노드들을 한번씩 탐색한다. 시작은 root node에서 출발하며 순회 방법에는 여러가기 방법이 존재한다.
inorder traversal(중위 순회)
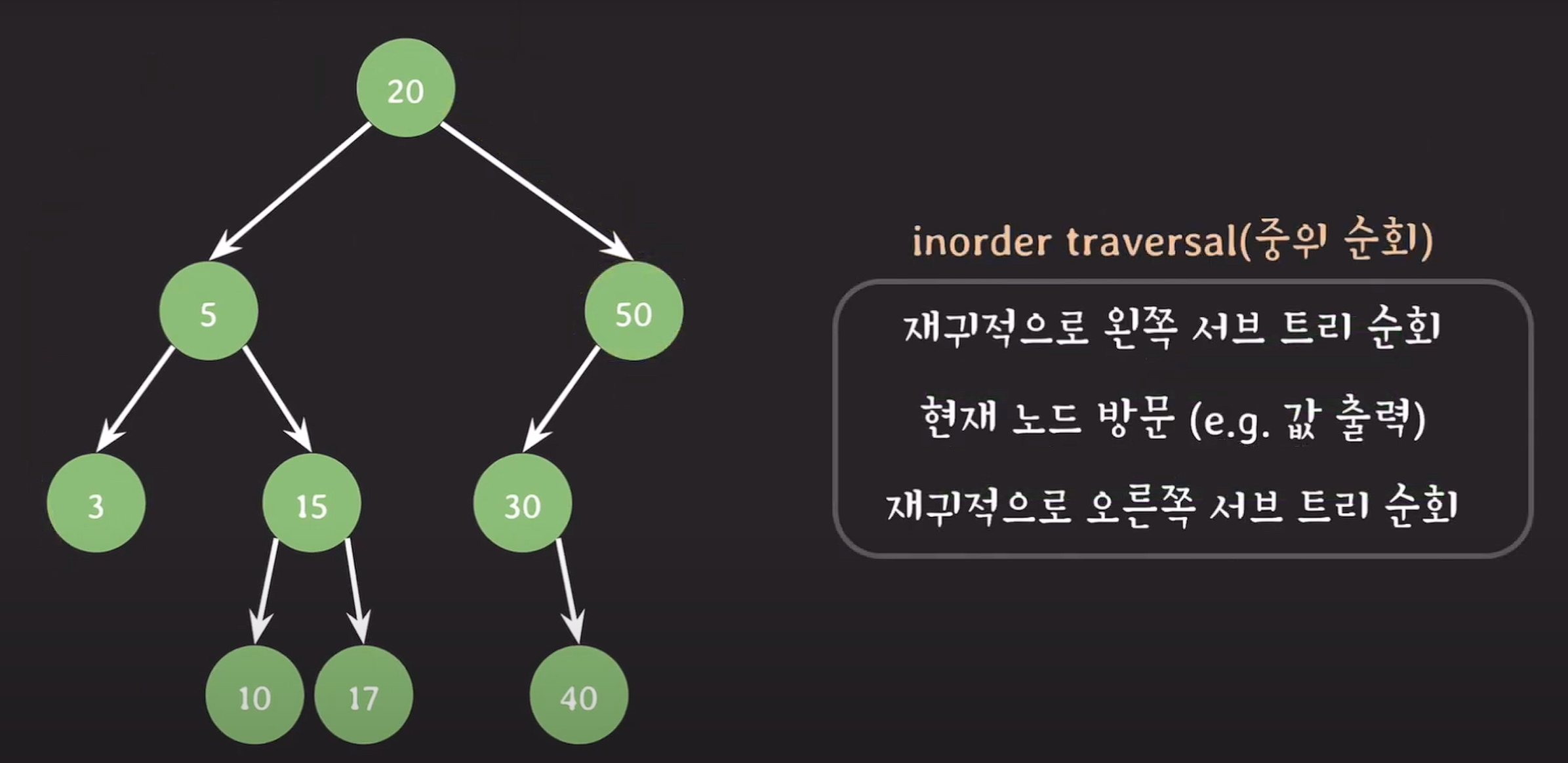
1) 20>5>3 더 이상 왼쪽 노드가 존재하지 않기 때문에 3을 출력
2) 3을 기준으로 오른쪽 노드가 존재하지 않기 때문에 5로 올라간 후 5노드의 왼쪽 순회가 더이상 존재하지 않기 때문에 5를 출력
3) 5>15>10 10출력
4) 10 출력 후 오른쪽 노드가 존재하지 않고 15기준으로 왼쪽 순회가 끝났기 때문에 15 출력 후 17로 이동 후 노드가 존재하지 않아 17 출력
5) root node를 기준으로 왼쪽 서브 트리의 순회가 모두 끝났기 때문에 root node까지 올라가며 20출력 후 root node 오른쪽 서브트리로 이동
6) 30 > 40 > 50을 순서대로 출력한다.
result : 3 5 10 15 17 20 30 40 50
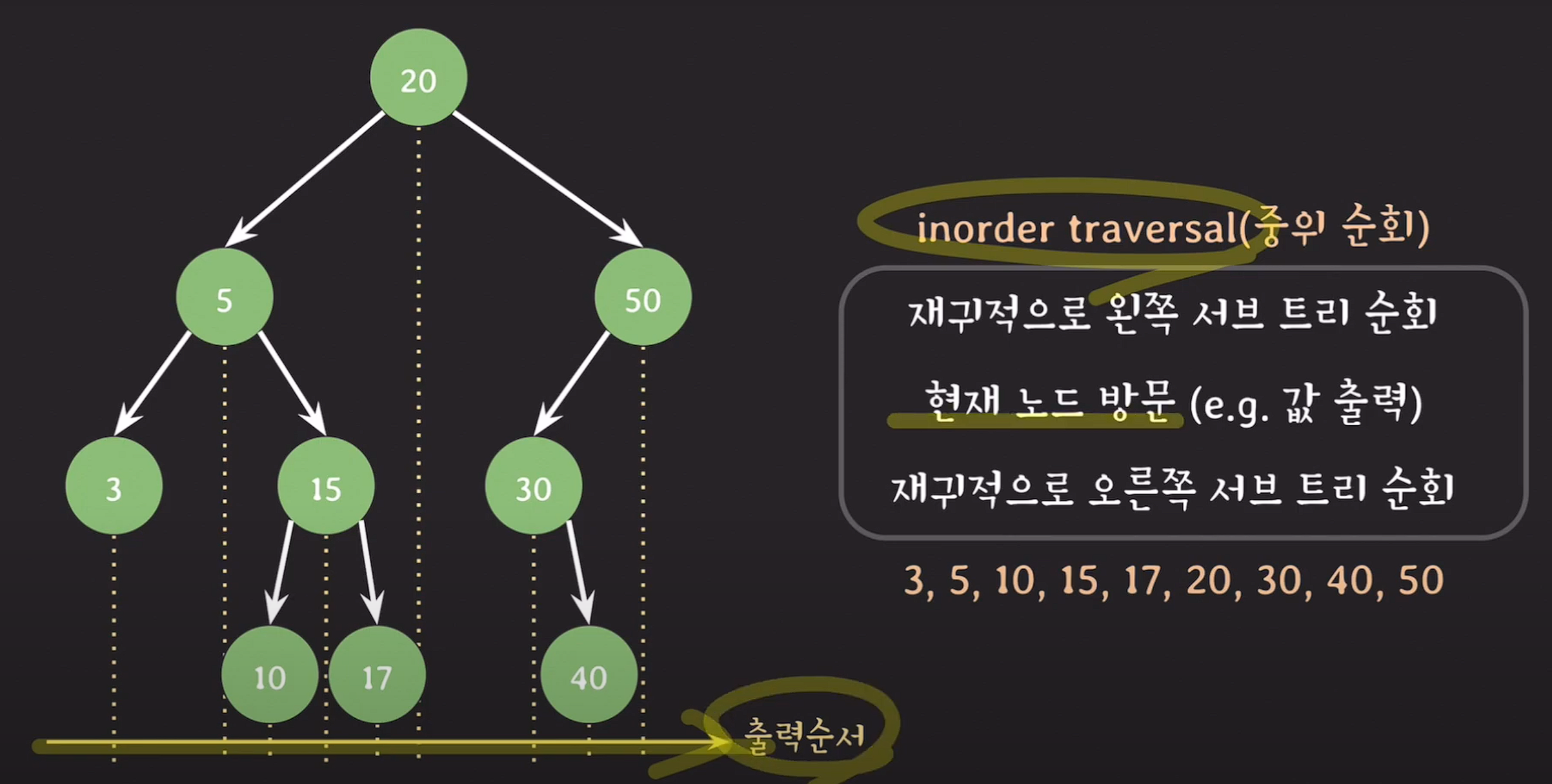
출력 결과를 확인해보면 작은 수 부터 차례대로 출력된다.
preorder traversal(전위 순회)
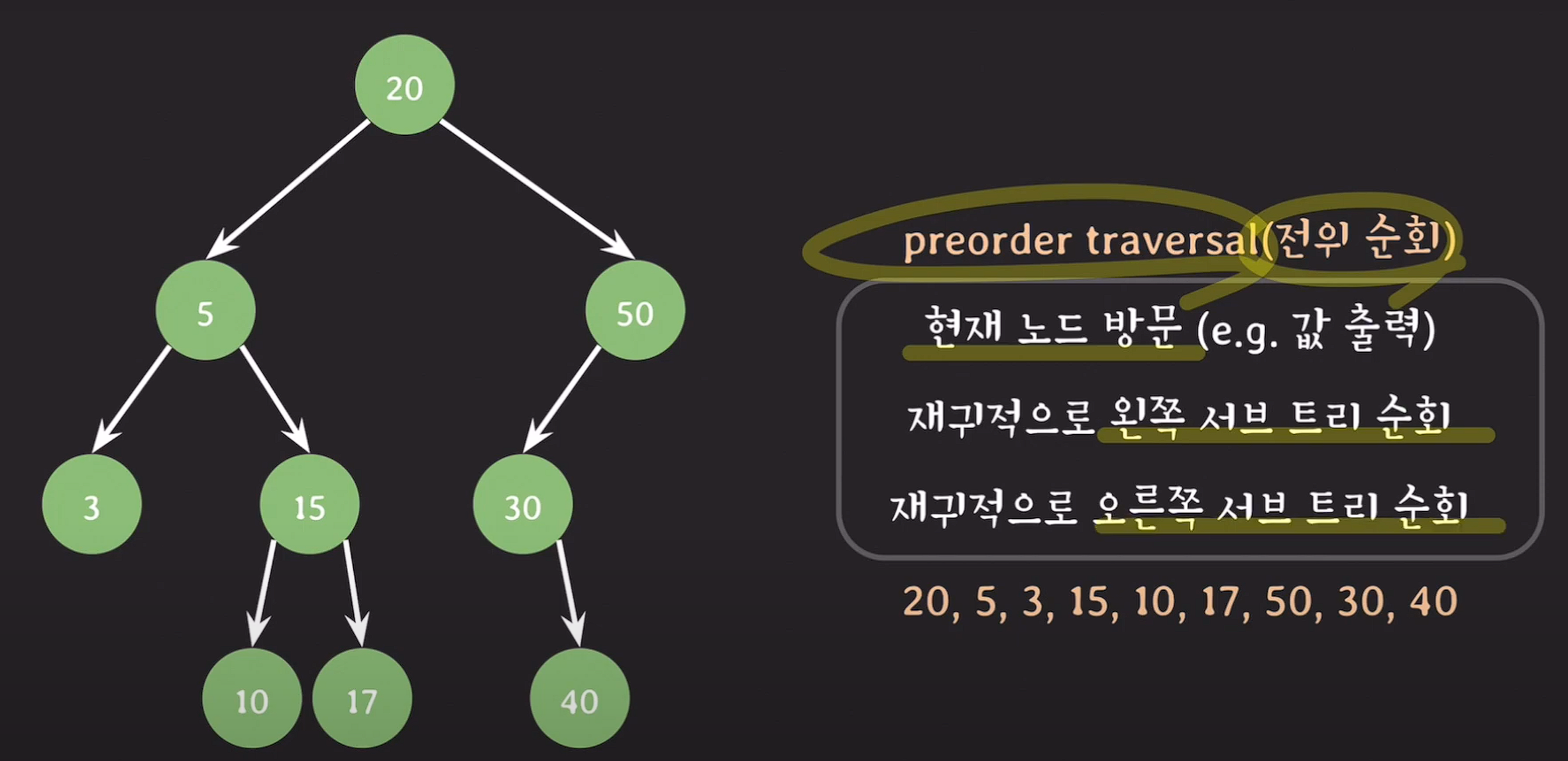
현재 노드를 먼저 방문하고 출력한다. 그 후 재귀적으로 왼쪽 서브 트리 순회 후 오른쪽 서브 트리를 순회 한다.
postorder traversal(후위 순회)
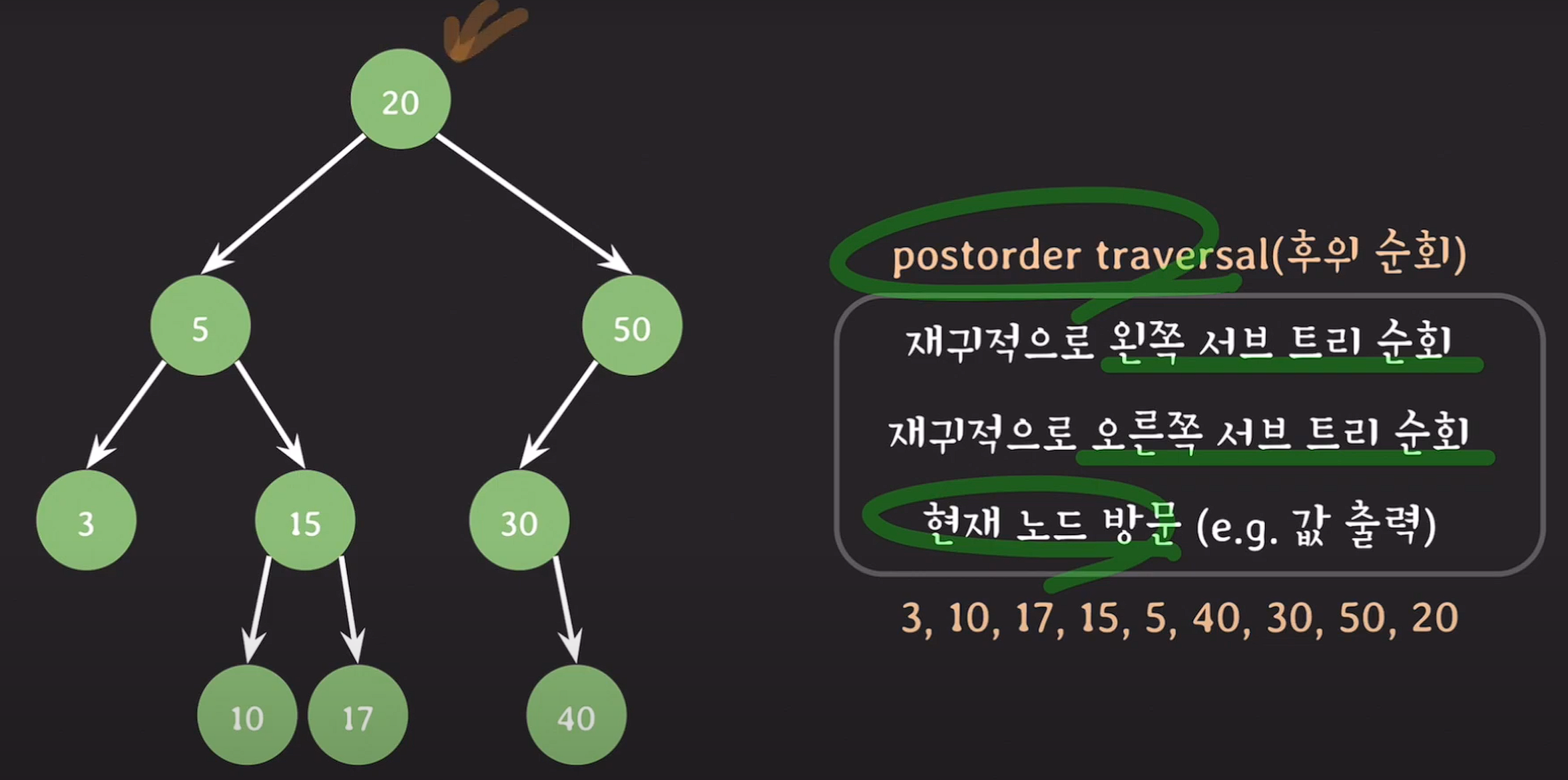
재귀적으로 왼쪽 서브 트리 순회, 재귀적으로 오른쪽 서브 트리 순회 후 현재 노드 방문 값 출력.
이진 탐색 트리의 삽입/삭제

삽입
insert(50); insert(70); insert(90); insert(80); insert(99);
insert(30); insert(40); insert(20);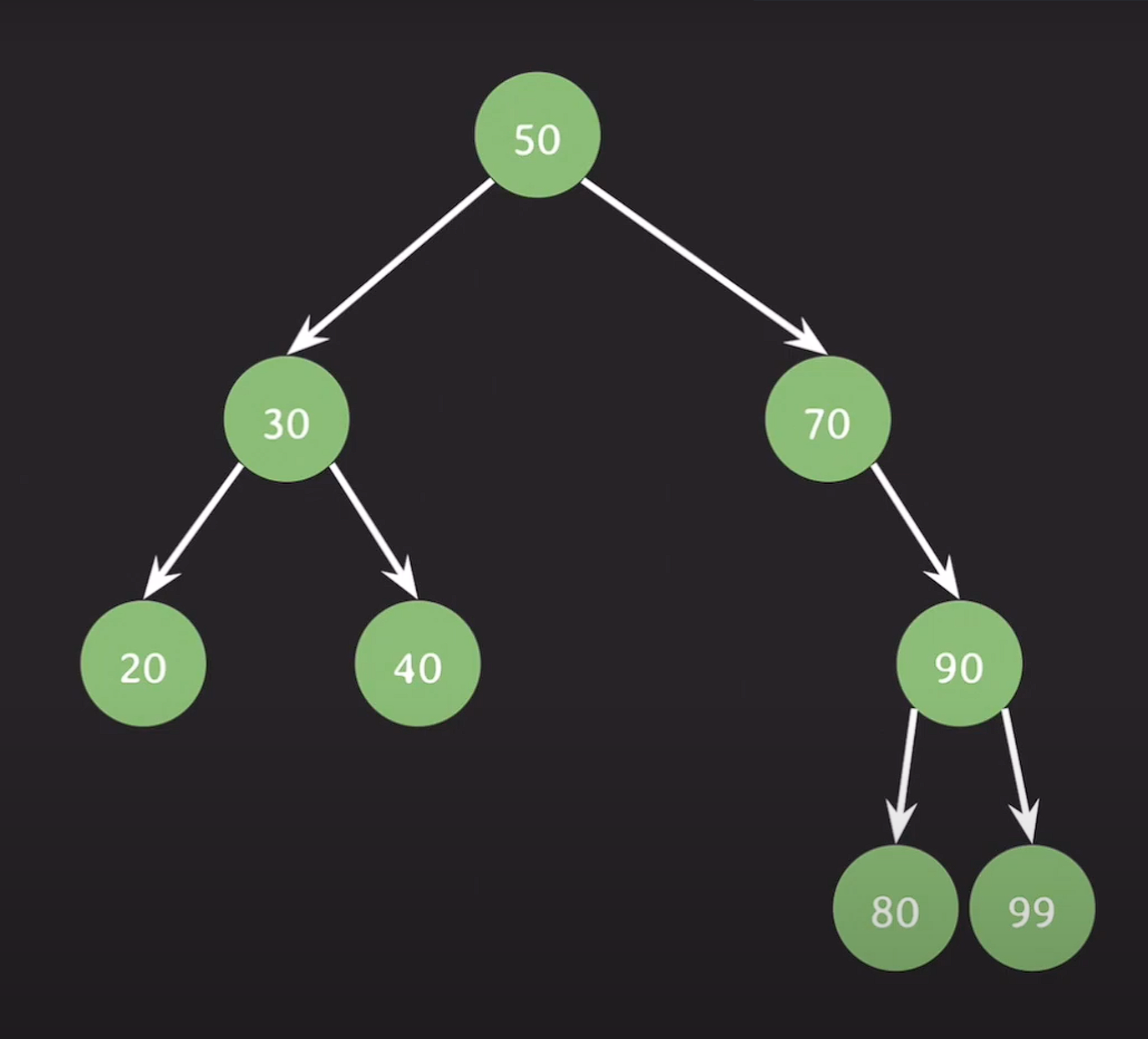
삭제
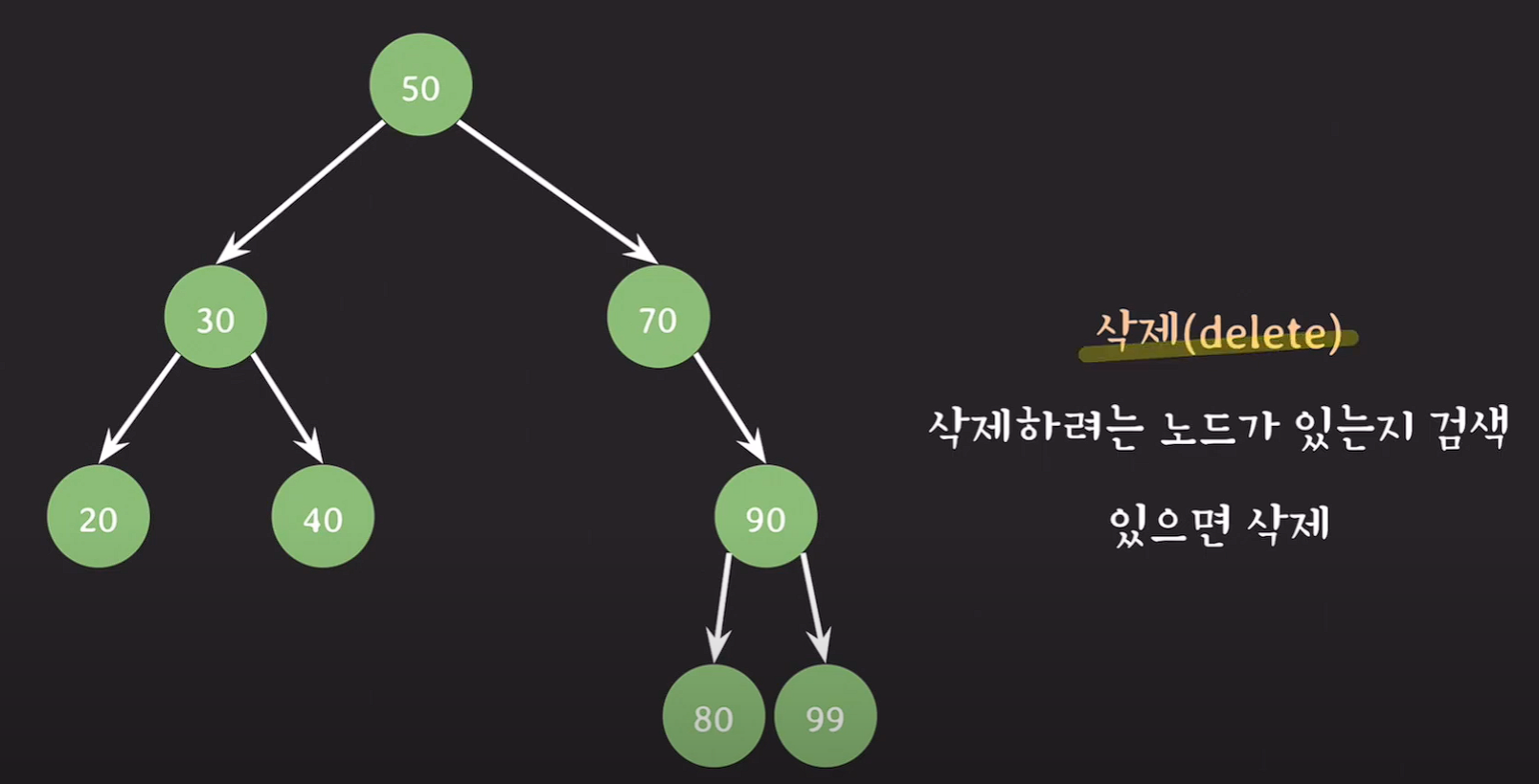
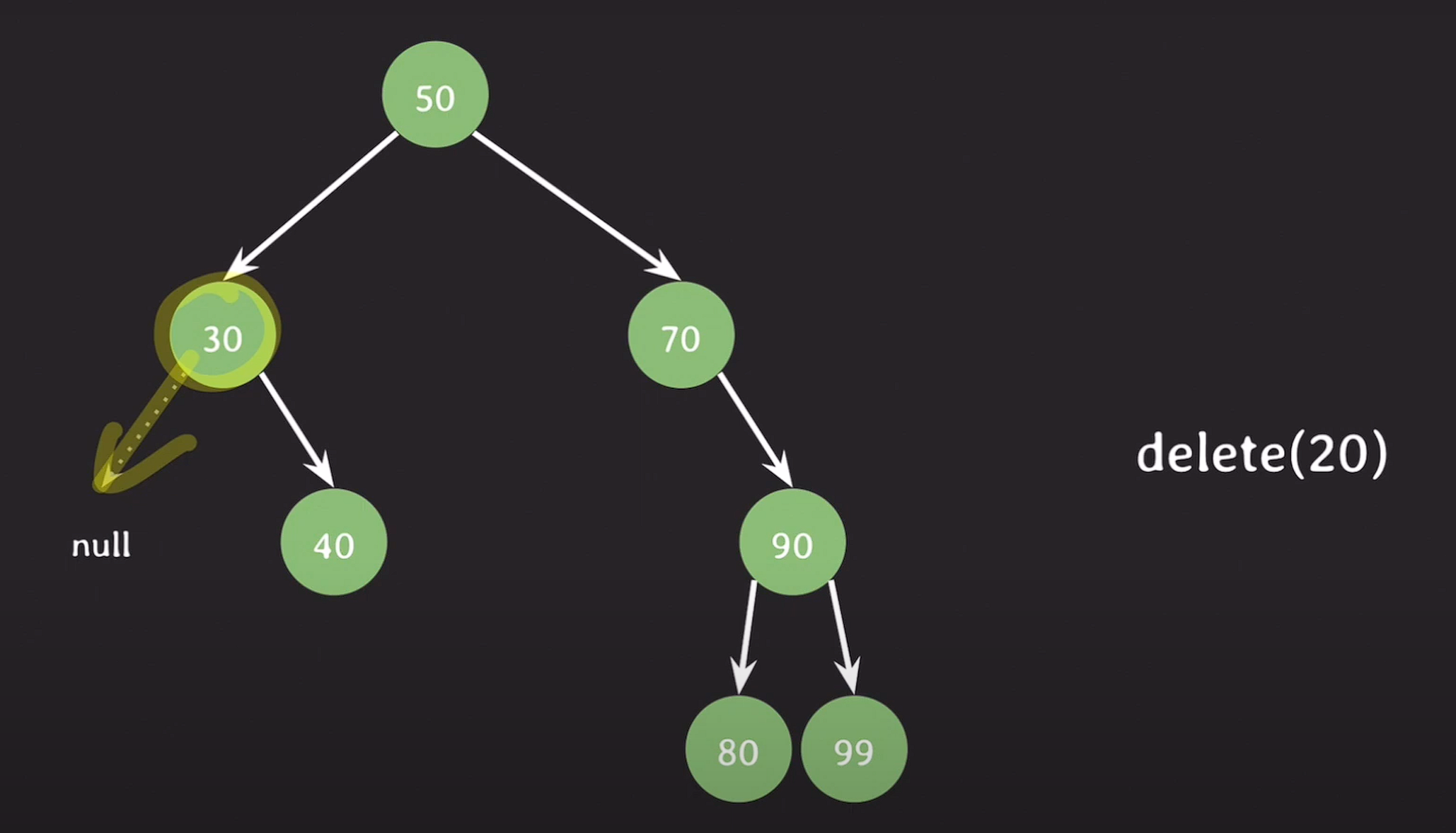
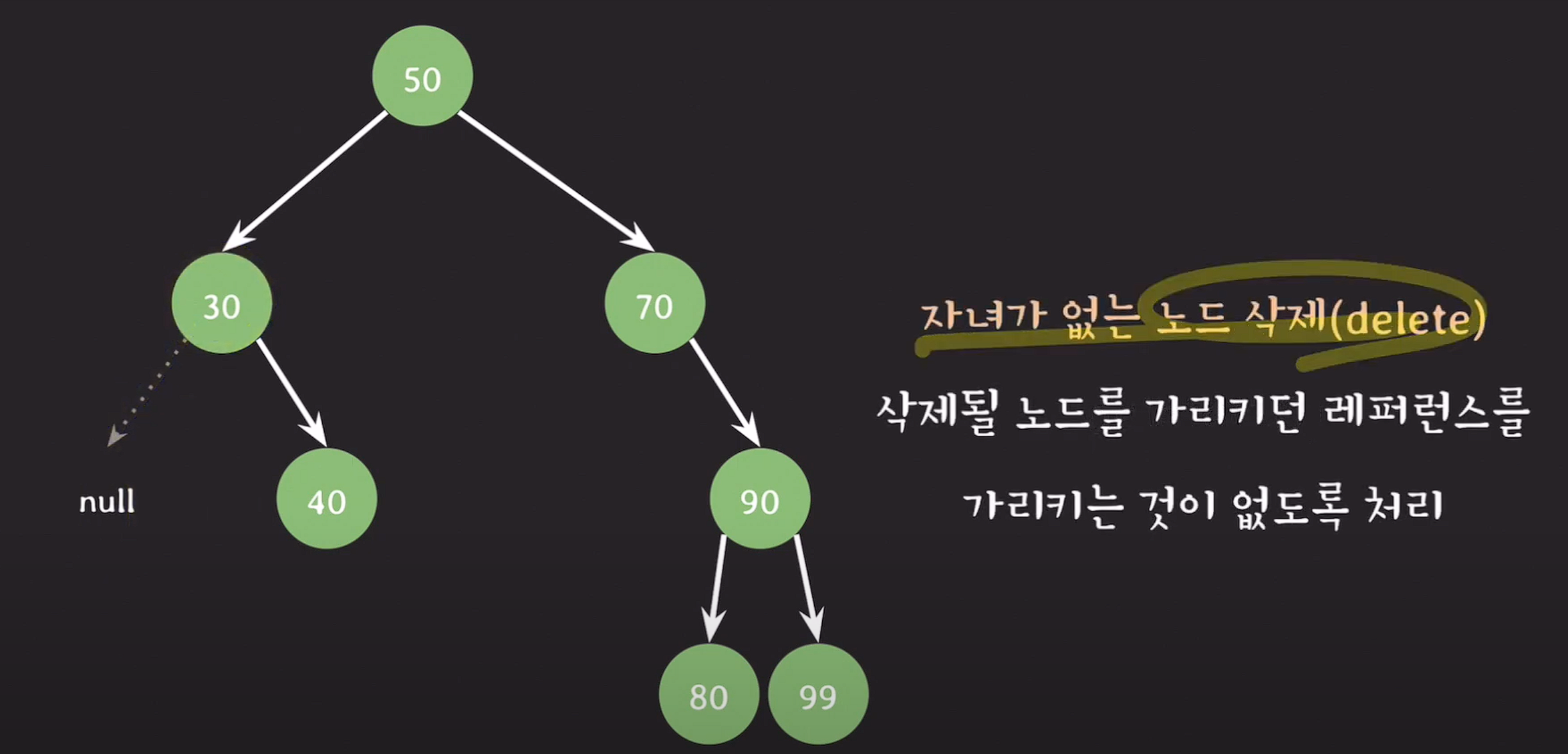
leaf node, 자녀가 없는 노드를 삭제 : 삭제될 노드를 가리키던 레퍼런스가 가리키는 것이 없도록 처리한다.
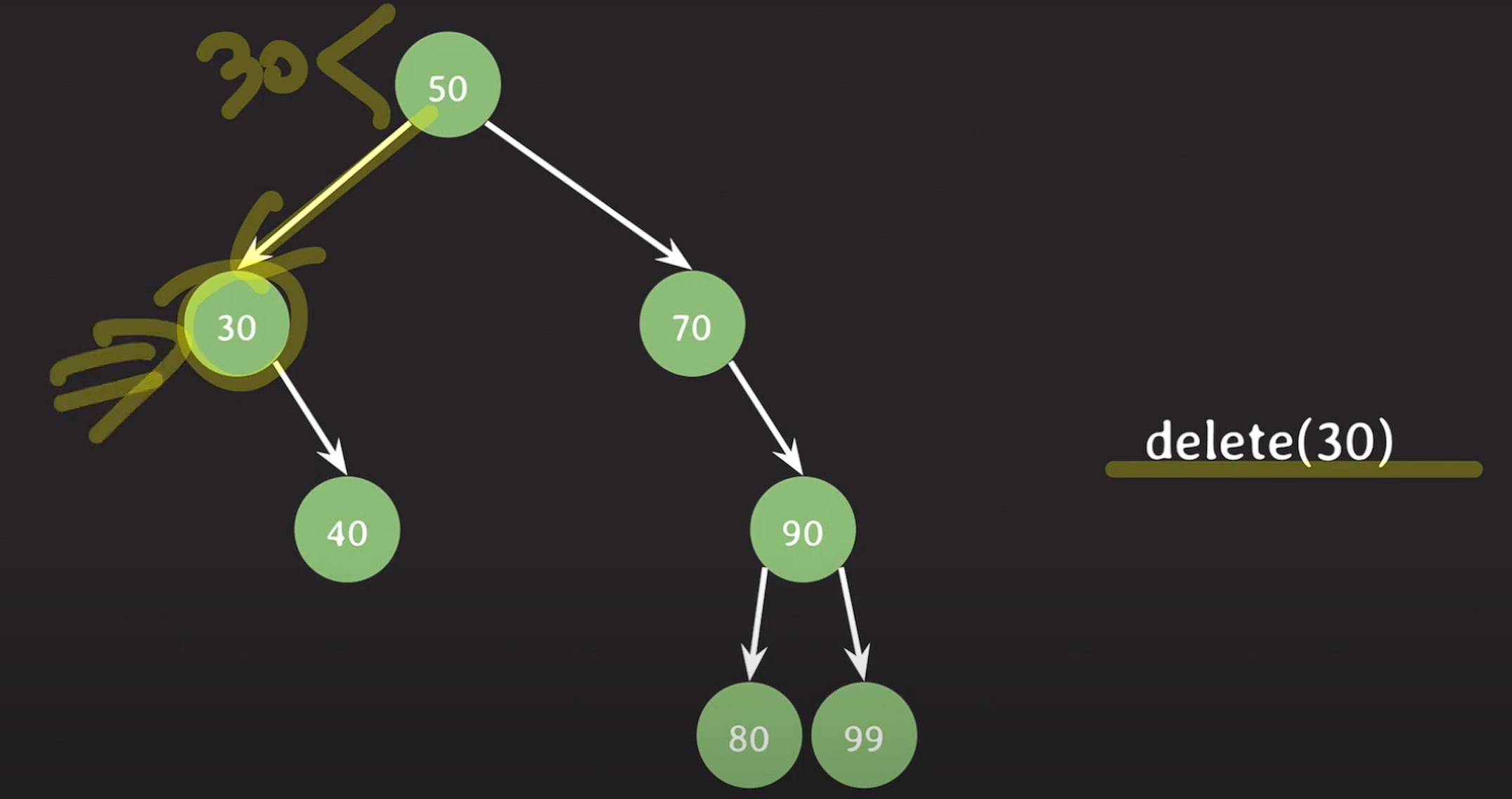
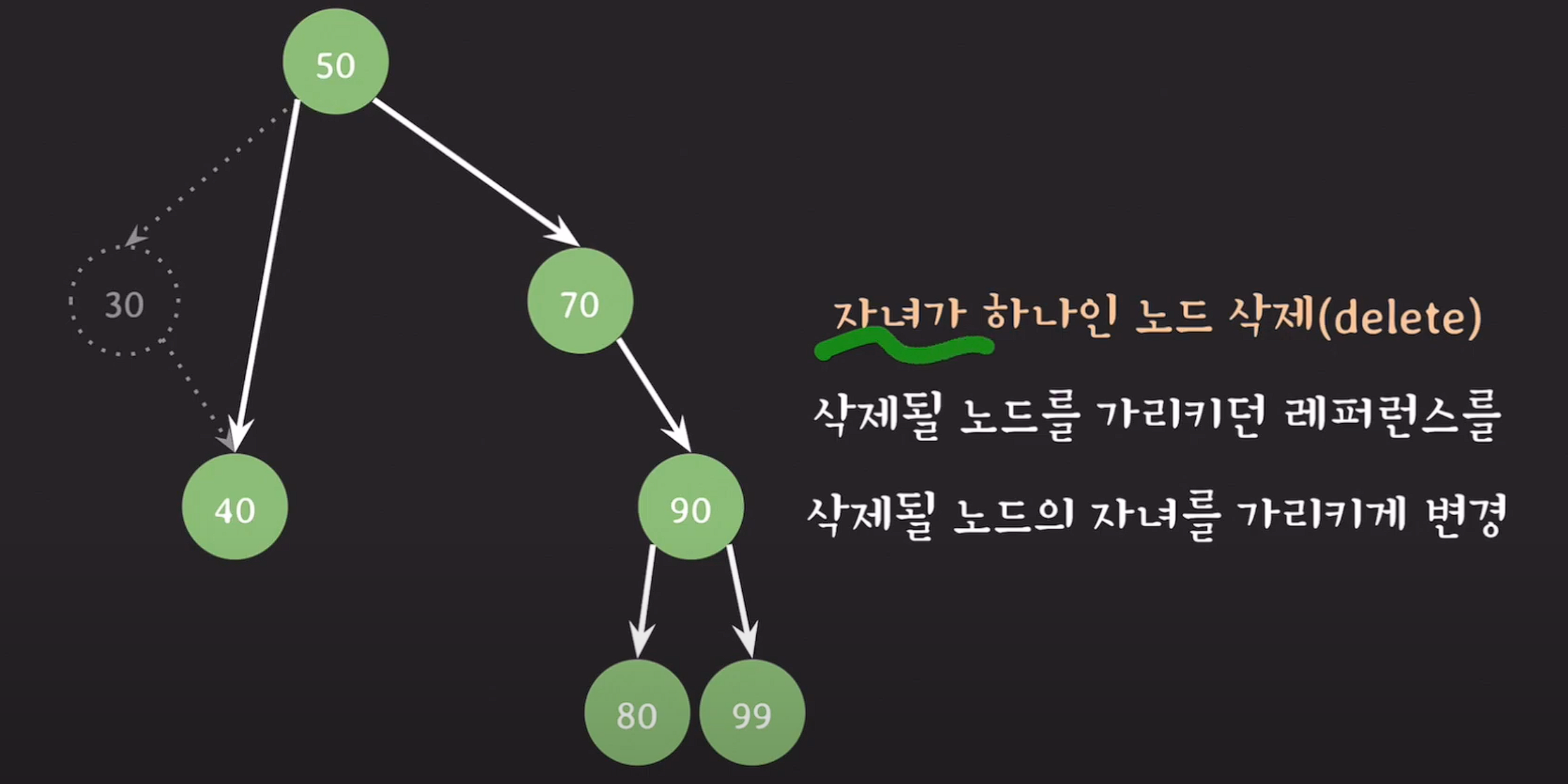
자녀가 하나인 노드 삭제 : 삭제될 노드를 가리키던 레퍼런스를 삭제될 노드의 자녀를 가리키게 변경한다.
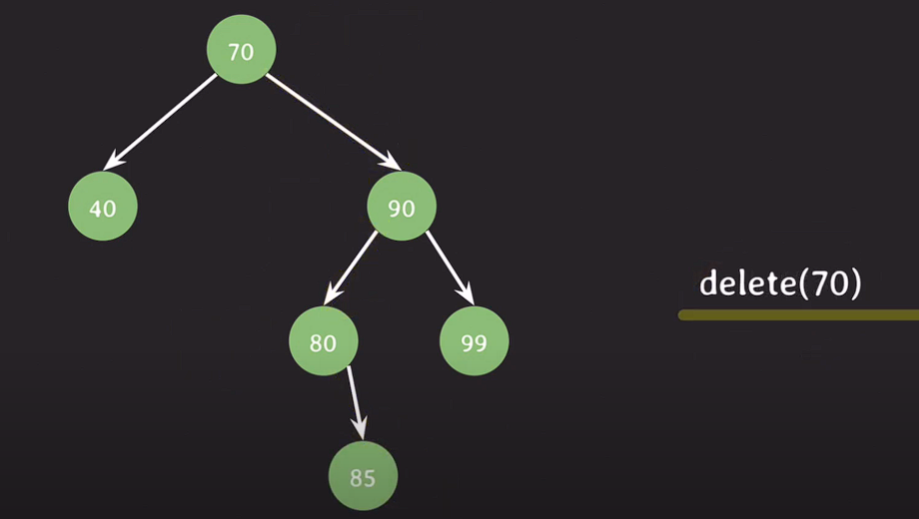
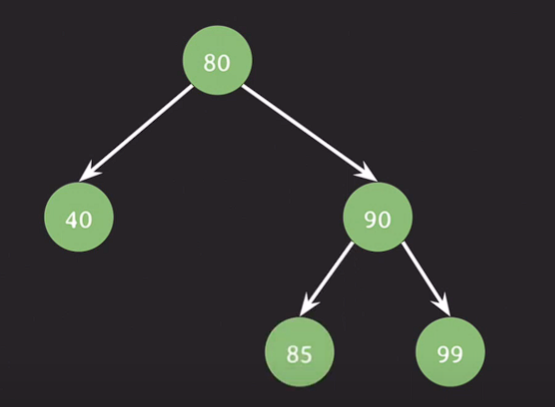
delete(50);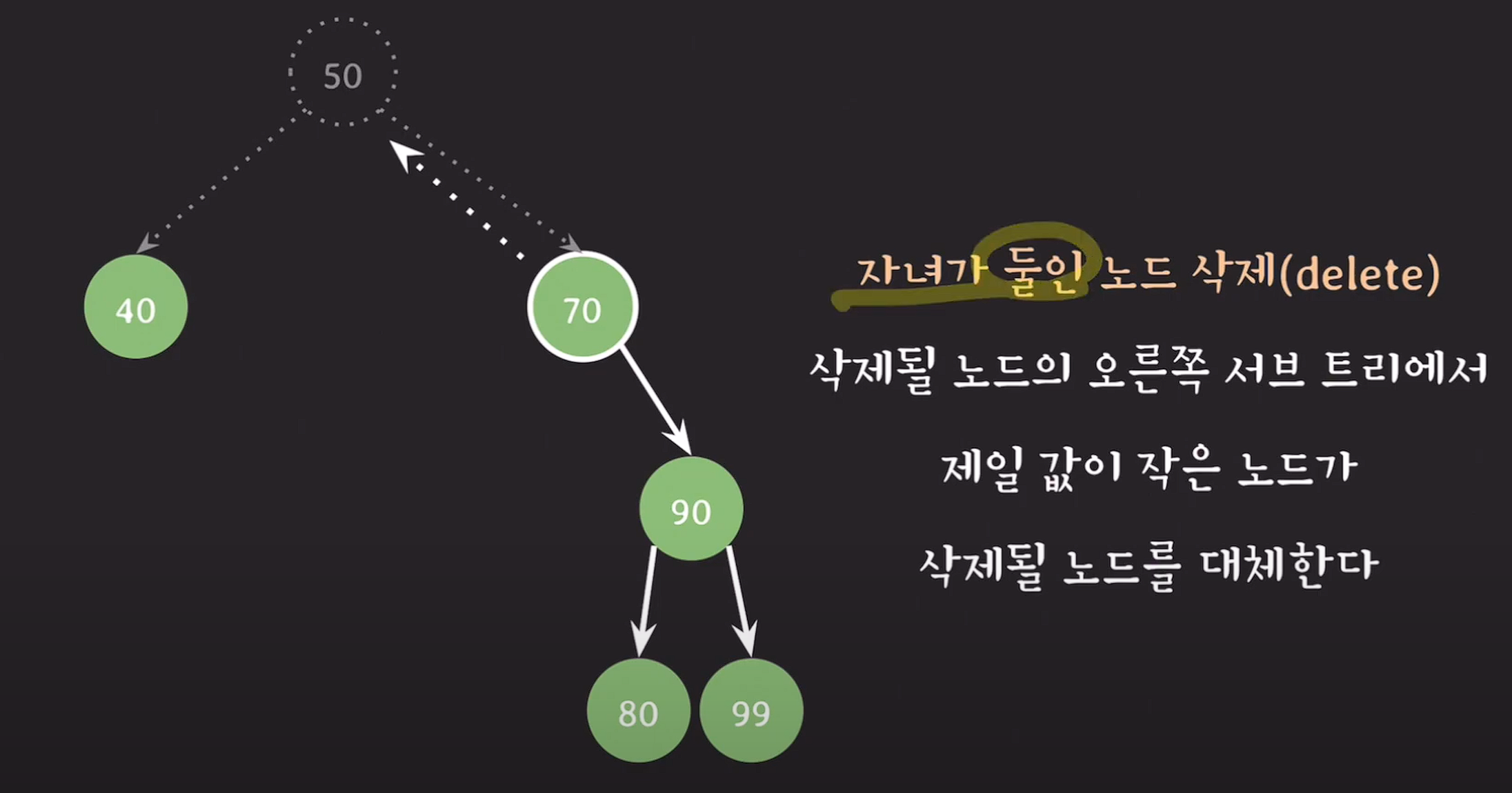
자녀가 둘인 노드 삭제 : 삭제될 노드의 왼쪽 or 오른쪽 서브트리에서 대체할 노드를 선택.
1) 왼쪽 : 삭제될 노드의 값보다 작지만 가장 큰값이 삭제될 노드를 대체한다.
2) 오른쪽 : 삭제될 노드의 값보다 크지만 가장 작은값이 삭제될 노드를 대체한다.
==> 선임자 or 후임자가 삭제될 노드를 대체한다.
==> 이진 탐색 트리의 특성을 유지시킬 수 있다.
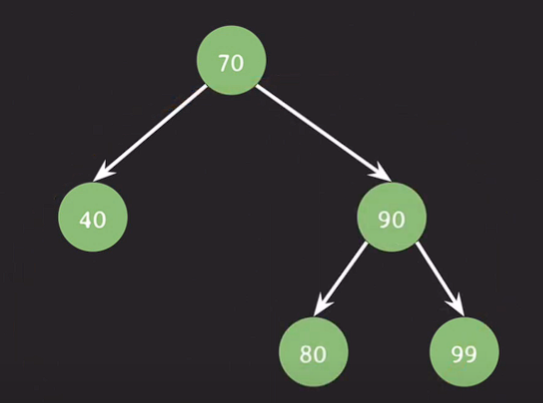
add(85);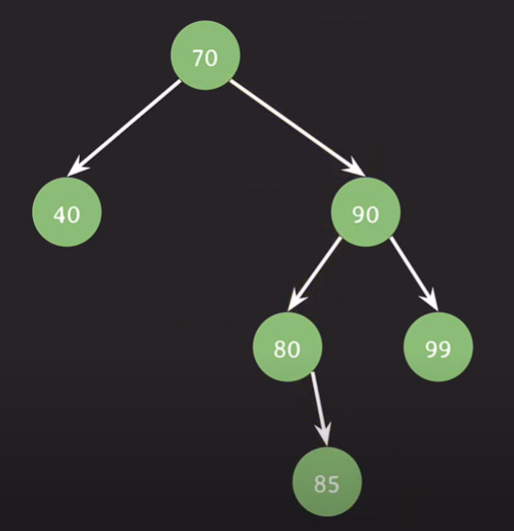
시간 복잡도

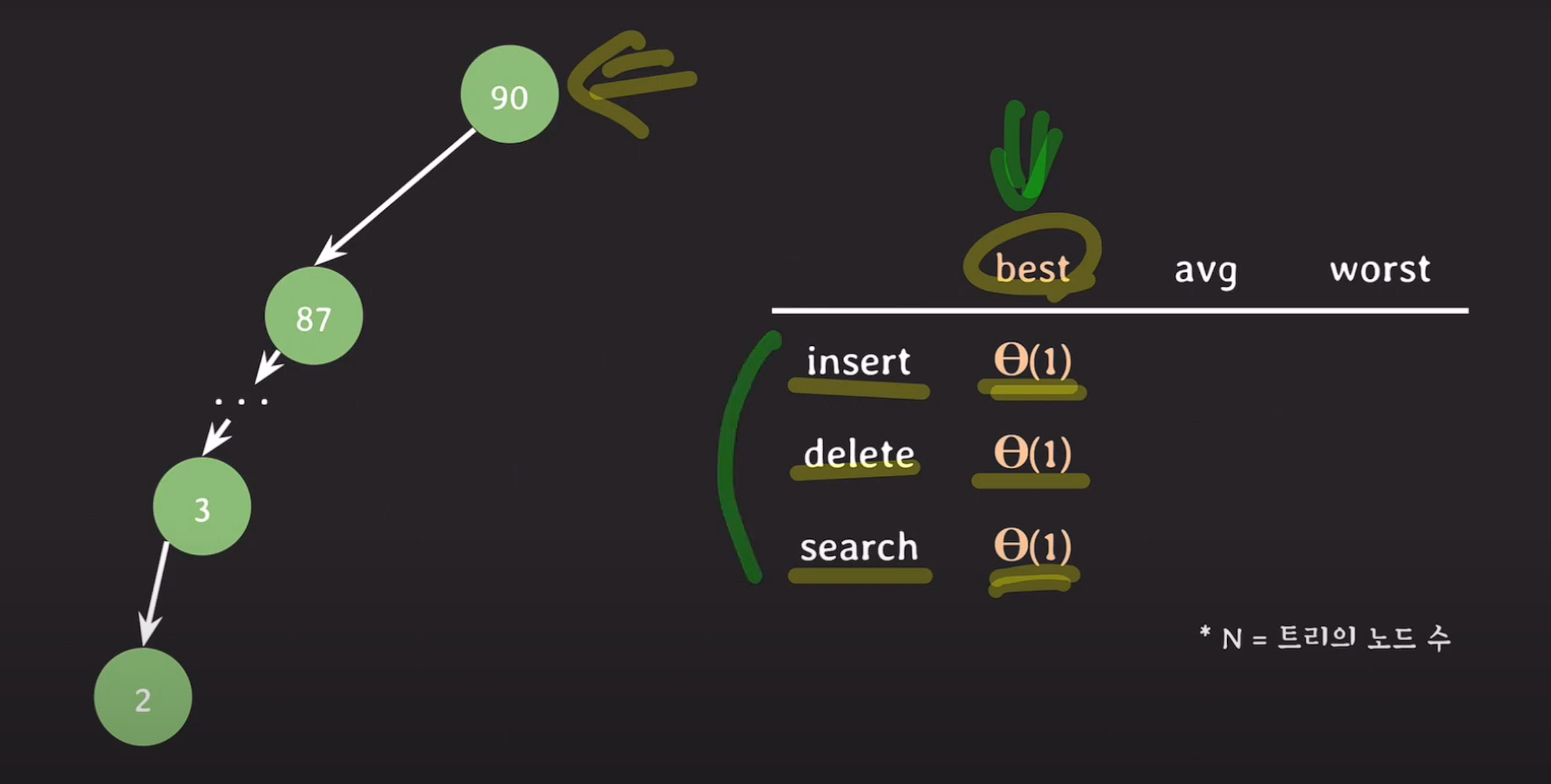
root node를 추가, 삭제, 검색한다 가정하면 best case는 세타(1)
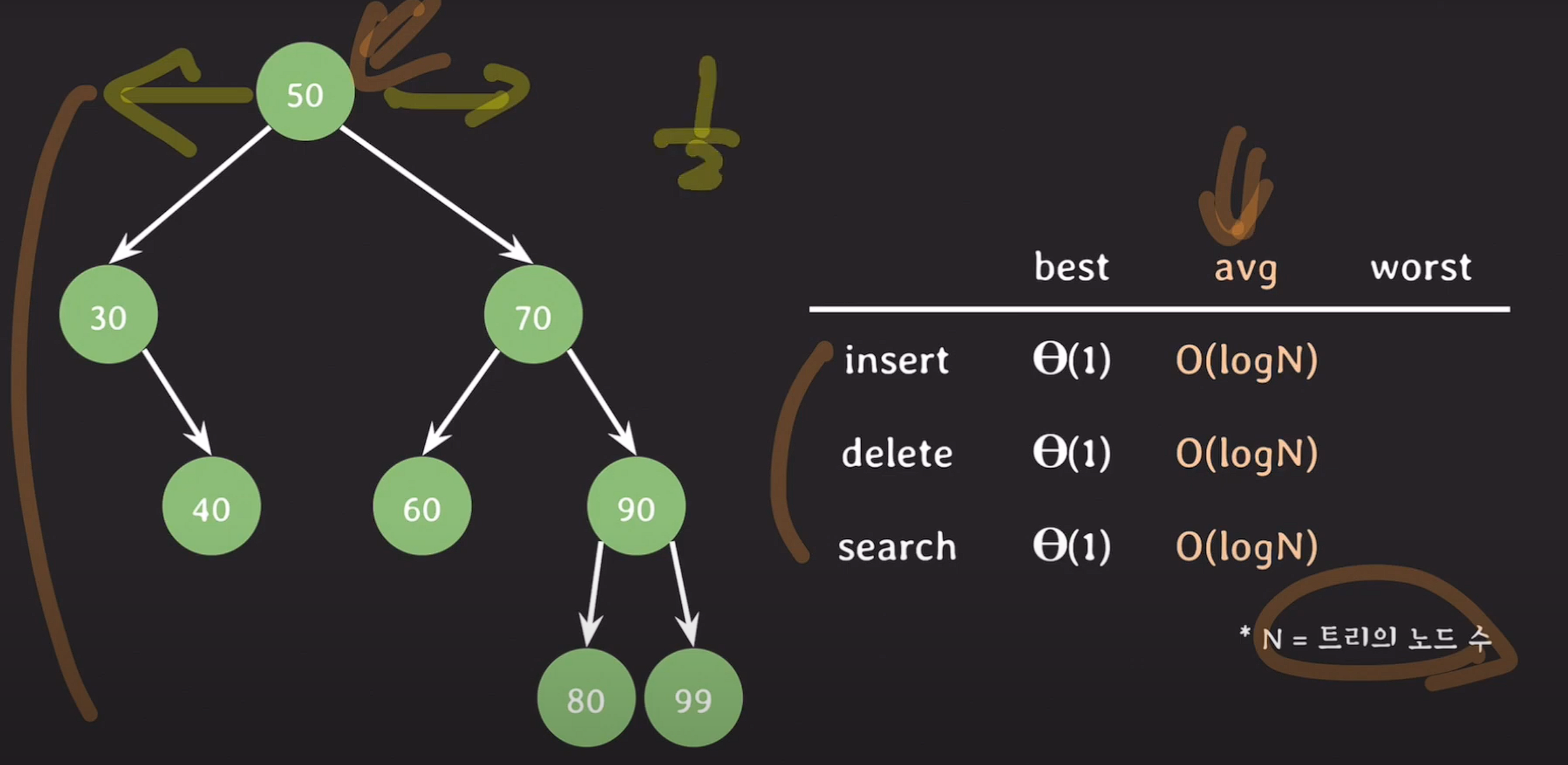
이진탐색 시 평균 O(logN), 1/2씩 줄여 나갈 수 있다.

이진 탐색 트리의 장점

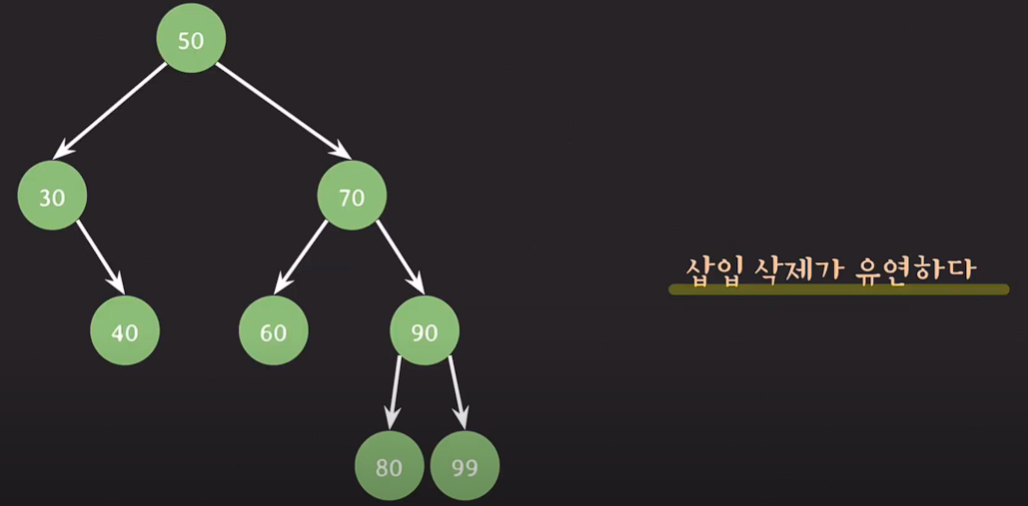
삽입, 삭제가 유연하다.
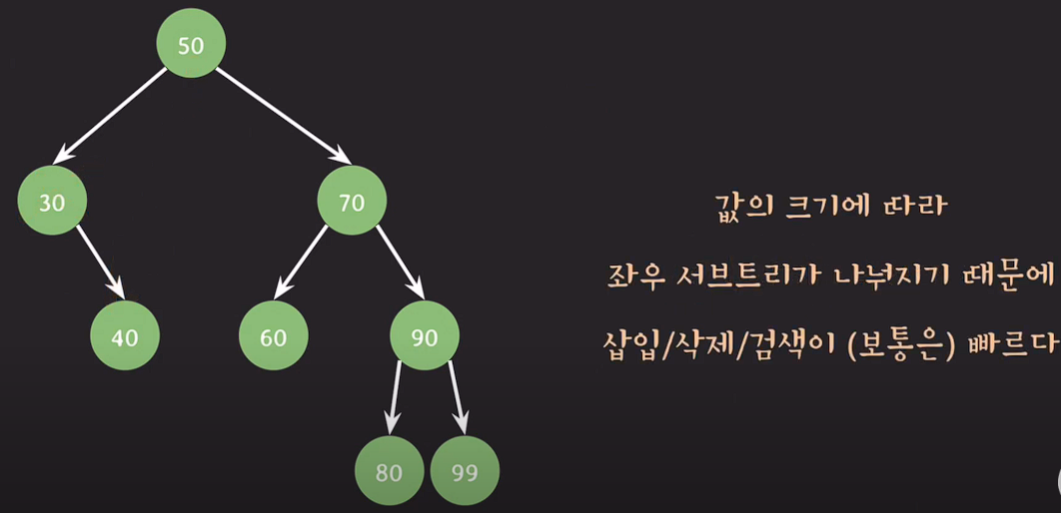
값의 크기에 따라 좌우 서브트리가 나눠지기 때문에 삽입/삭제/검색이 빠르다.
값의 순서대로 순회가 가능하다. (inorder traversal)
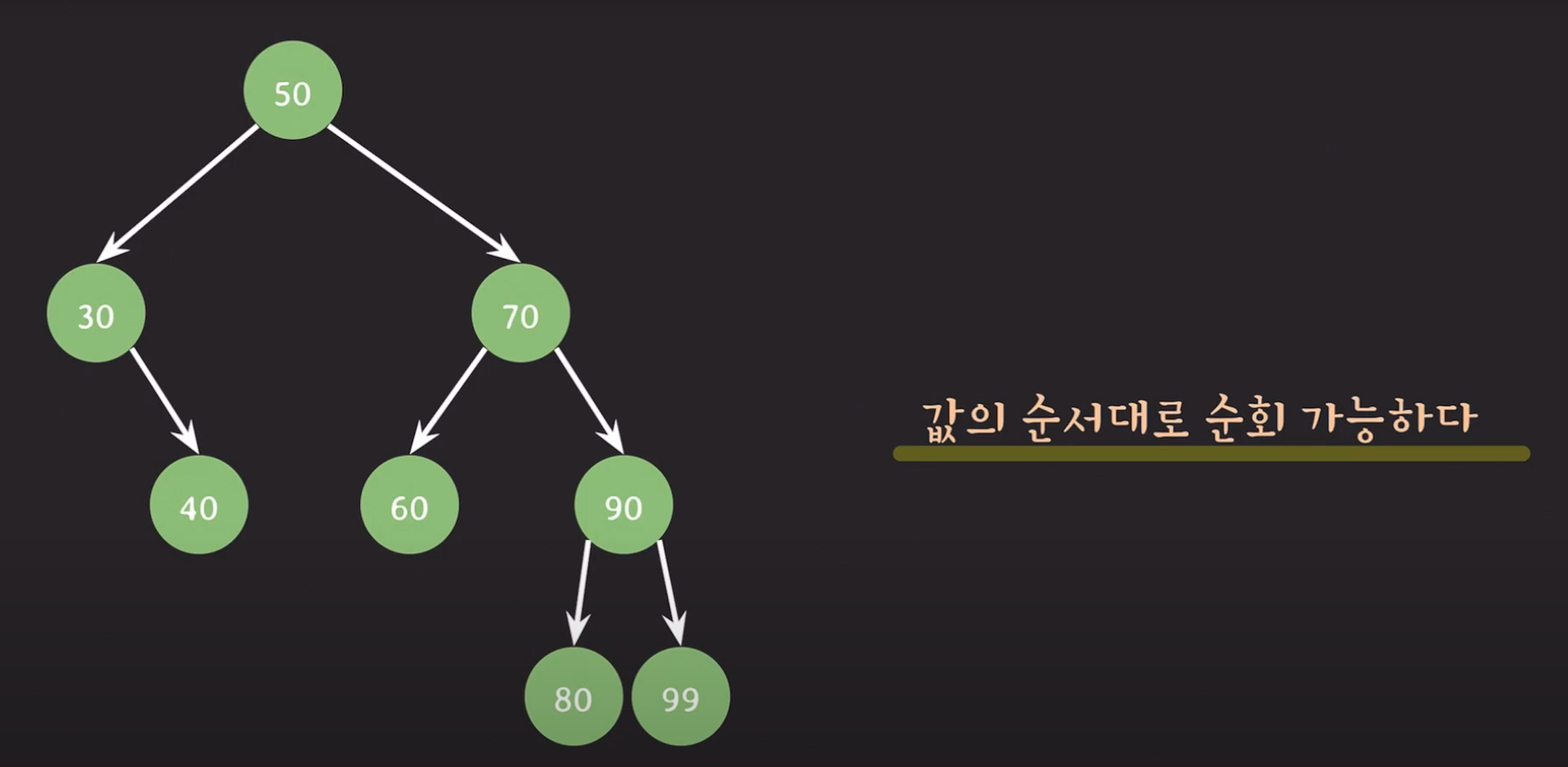
이진 탐색 트리의 단점

worst case
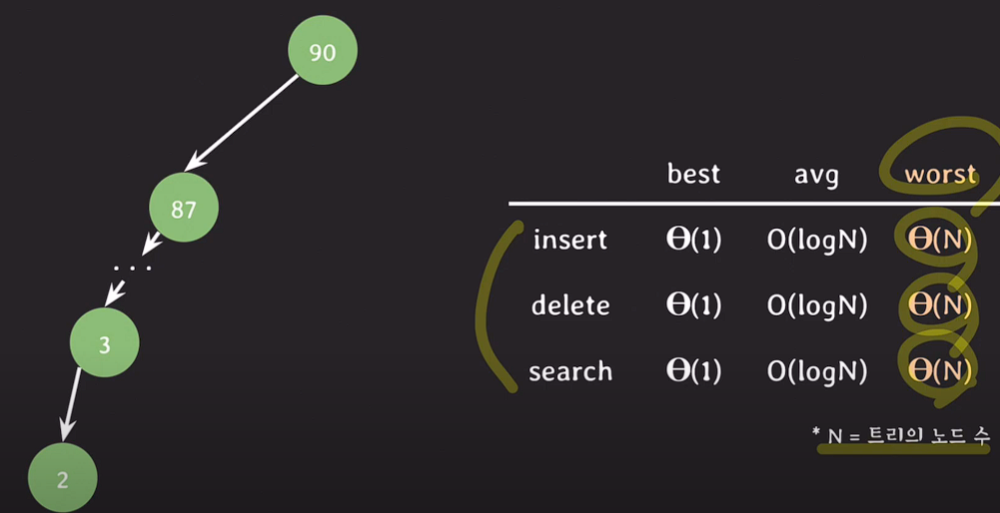
최악의 경우에 모든 노드를 검색해야한다.
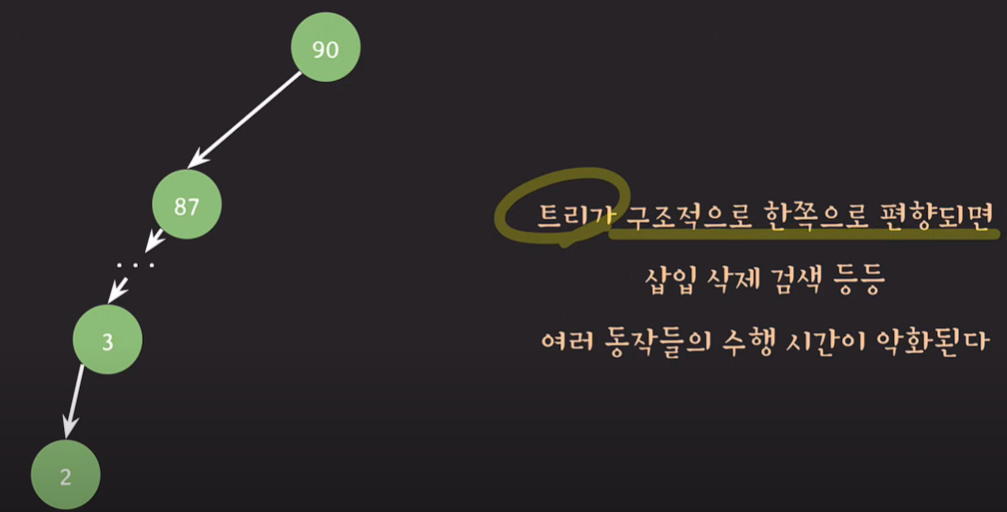
트리가 구조적으로 한쪽으로 편향되면 삽입/삭제/검색 등 여러 동작들의 수행시간이 악화된다.
ex) root node가 100인 상태에서 insert되는 값들이 모두 100보다 작은경우
단점 해결 케이스

이 문제를 해결하기 위해 스스로 균형을 잡는 이진 탐색 트리가 사용된다.
:: AVL트리, Red-Black 트리 => 한쪽에 편향되지 않은 이진 탐색 트리
:: worst case에서도 O(logN)