Tree & Binary Tree
Tree

Tree의 정의
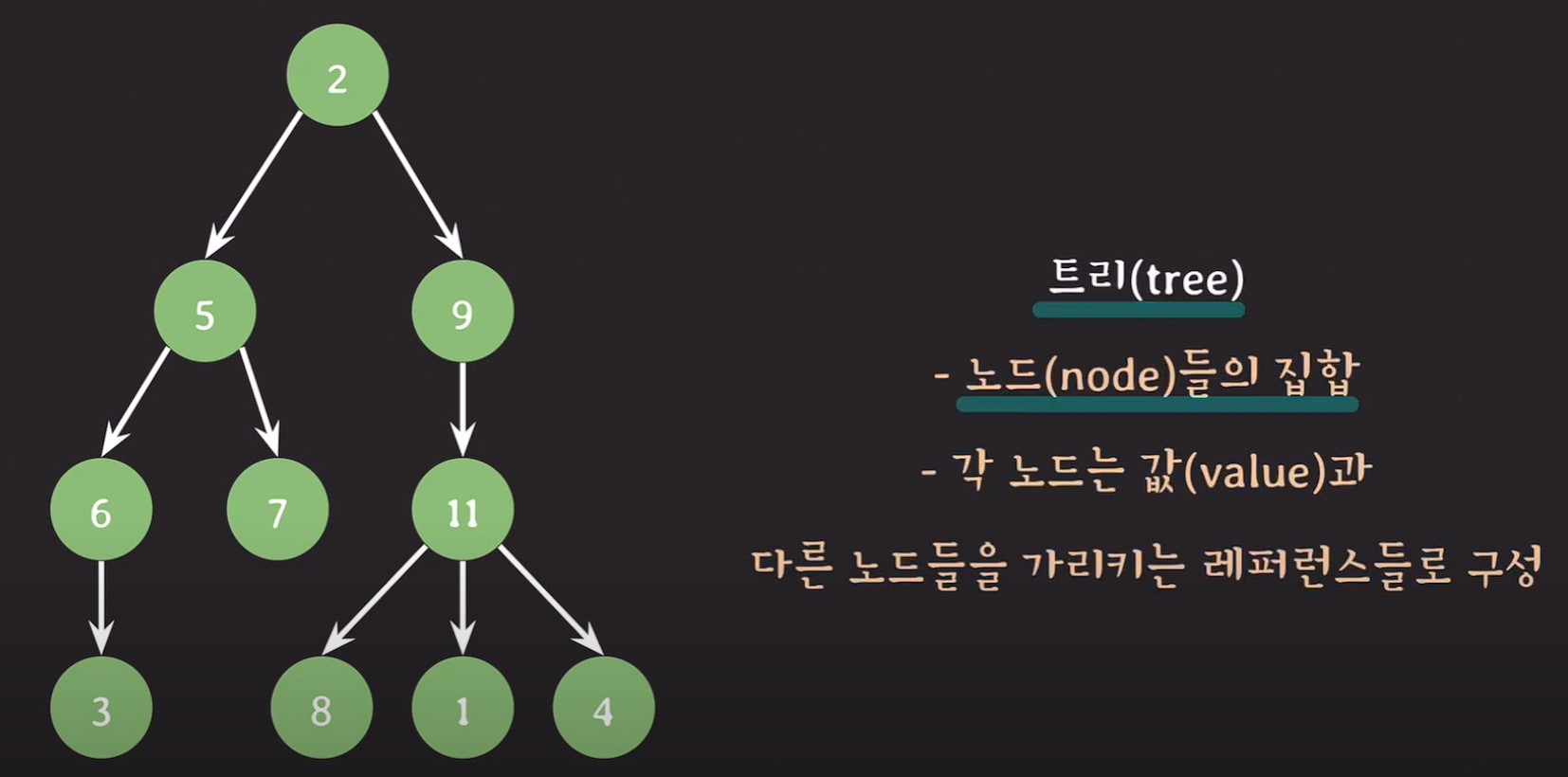
트리 : 노드들의 집합이며, 각 노드는 값과 다른노드를 가리키는 레퍼런스들로 구성되어있다.
ex) 트리 > 노드 > 값 + 레퍼런스
Tree관련 용어
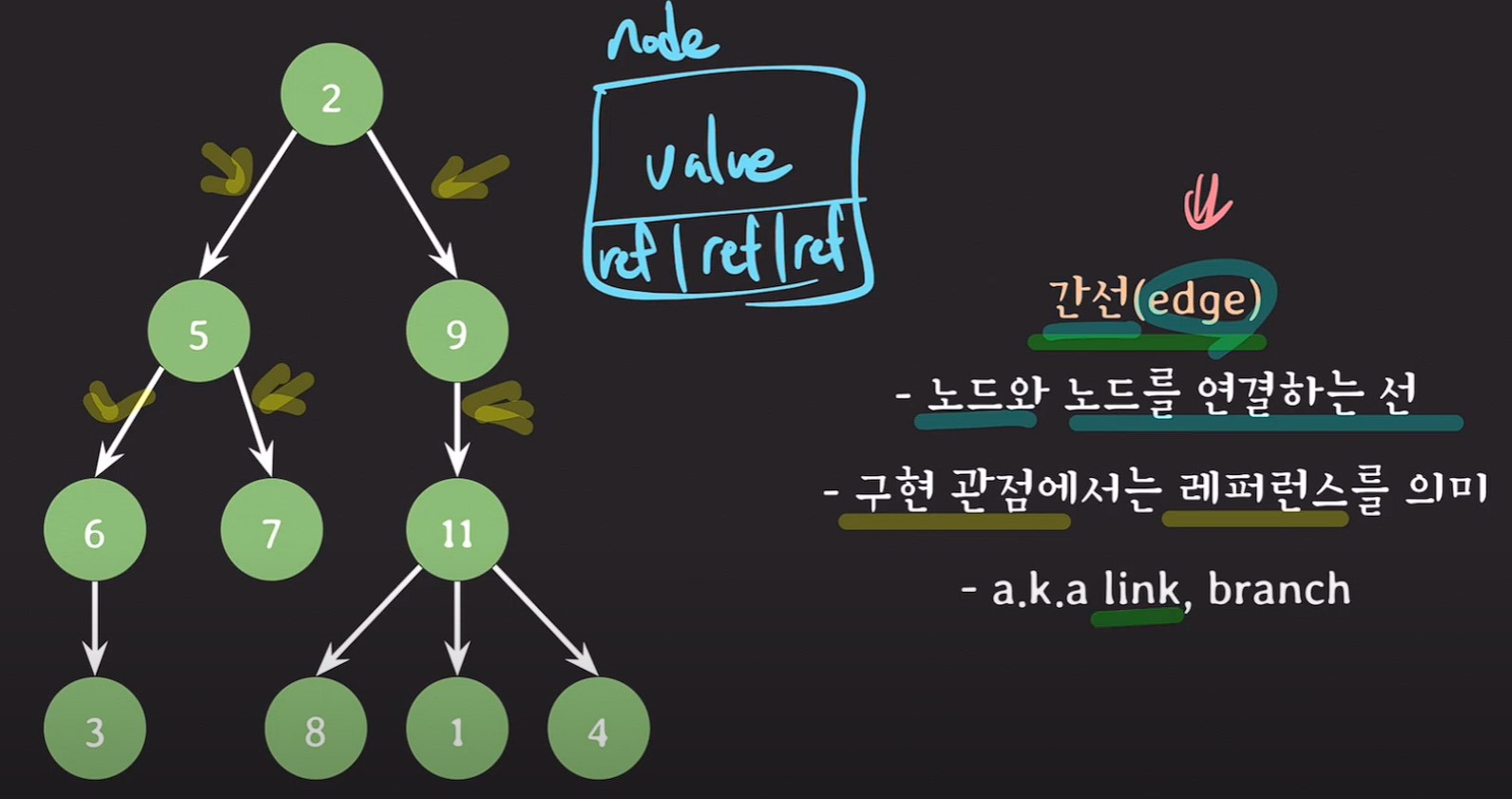
간선(edge) : 노드와 노드를 연결하는선, 구현관점에서 레퍼런스를 의미한다.
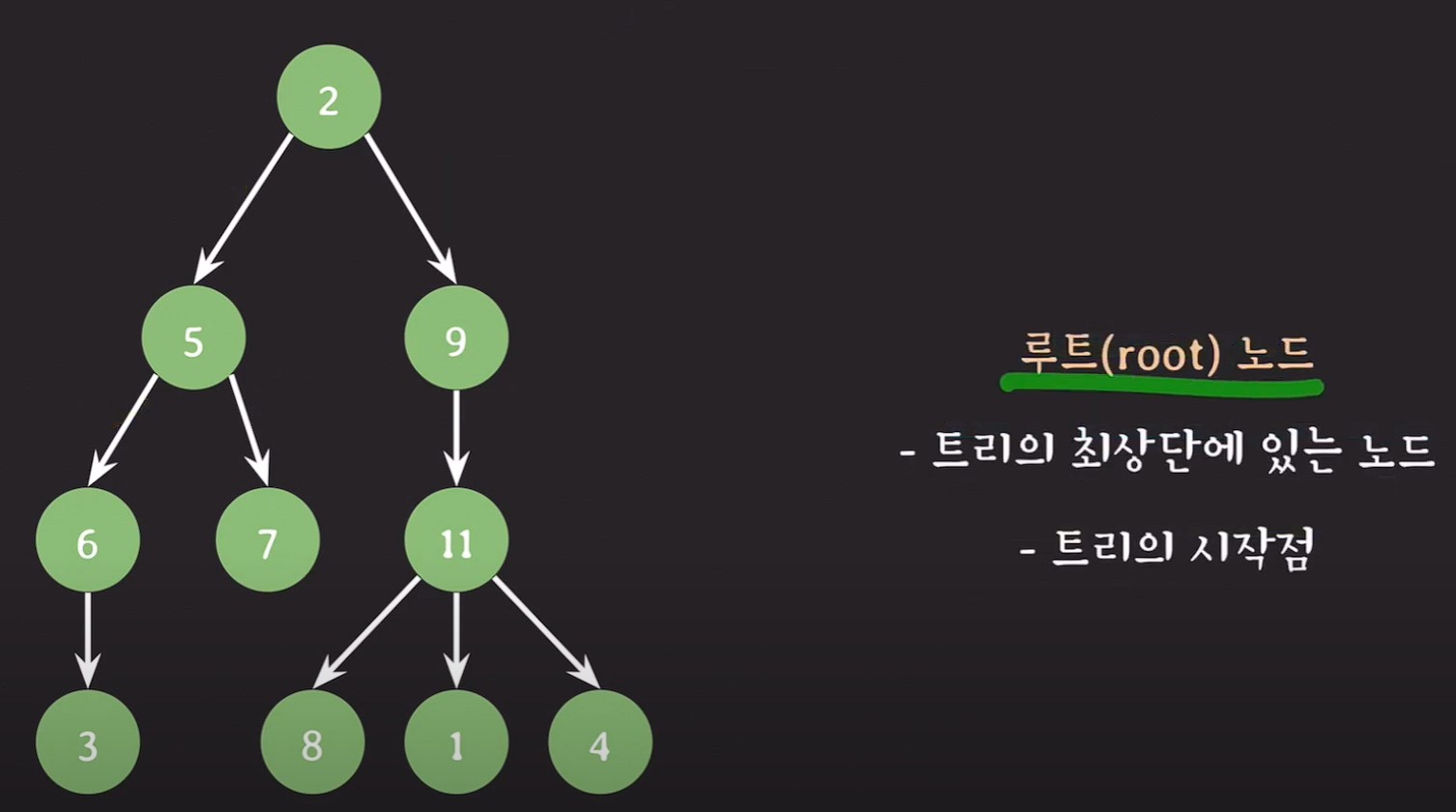
루트노드(root node) : 트리의 최상단에 위치한 노드이며, 트리의 시작점이다.
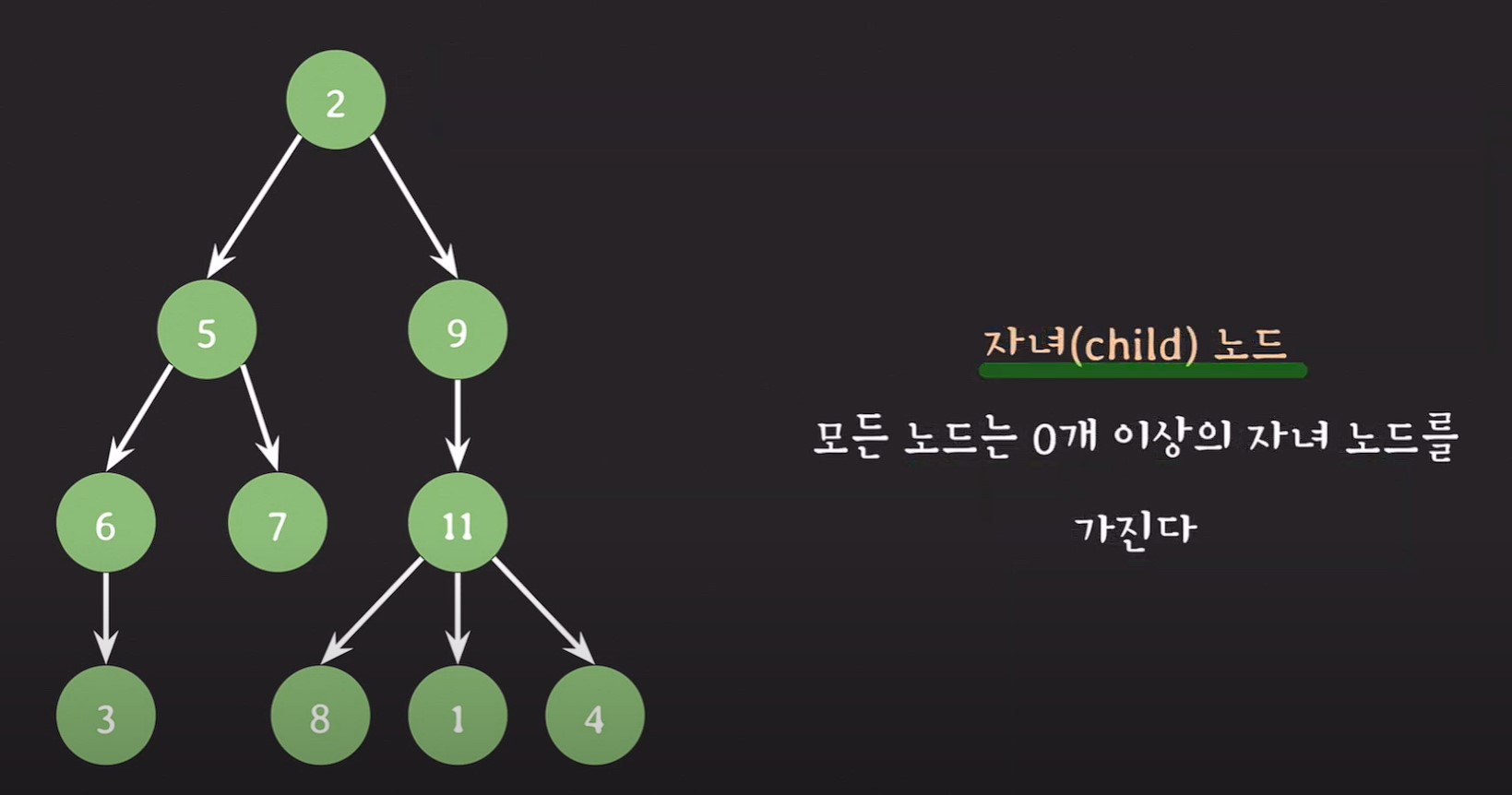
자녀노드(child node) : 모든 노드는 0개이상의 자녀노드를 가진다. (0~...)
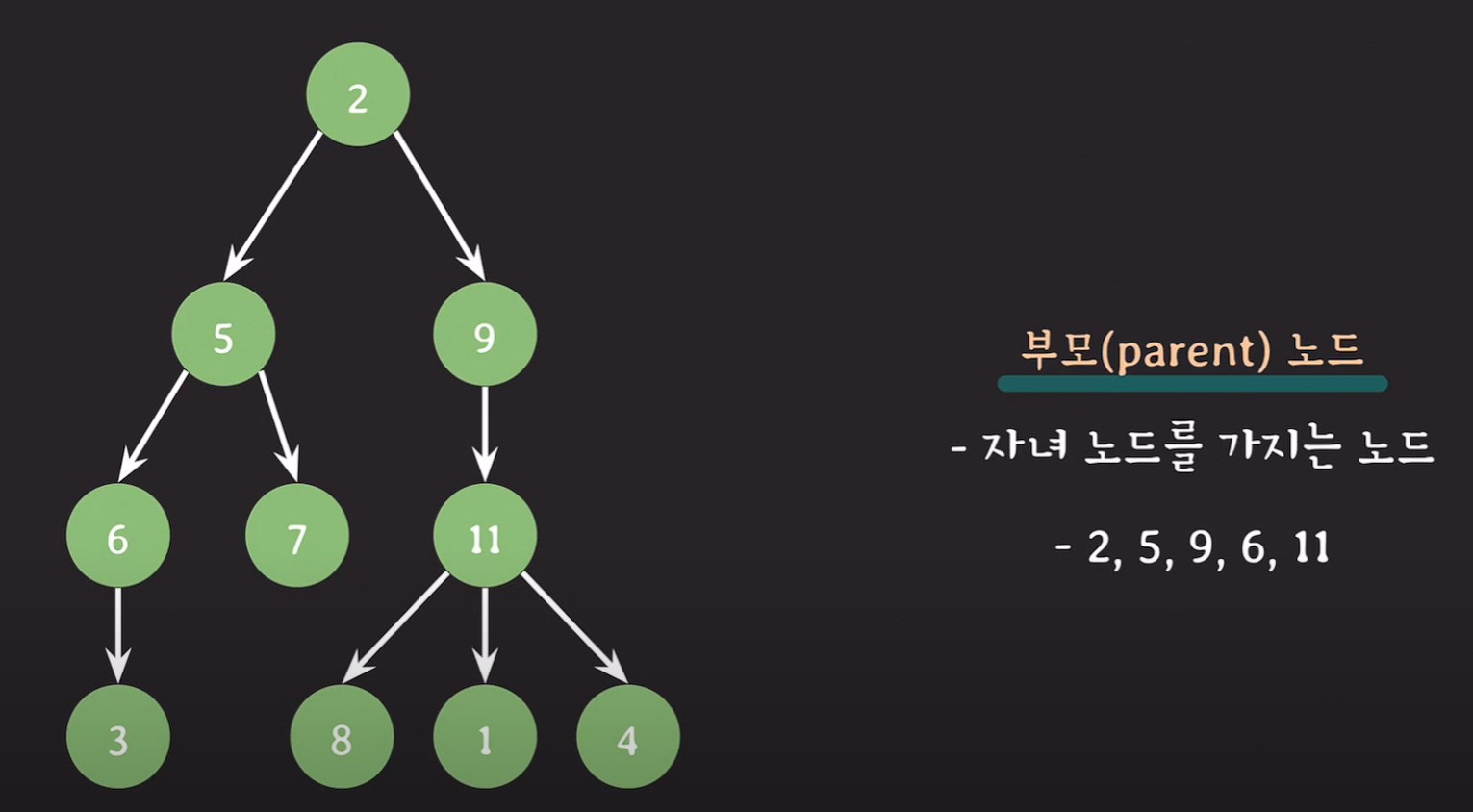
부모노드(parent node) : 자녀 노드를 가지는 노드들
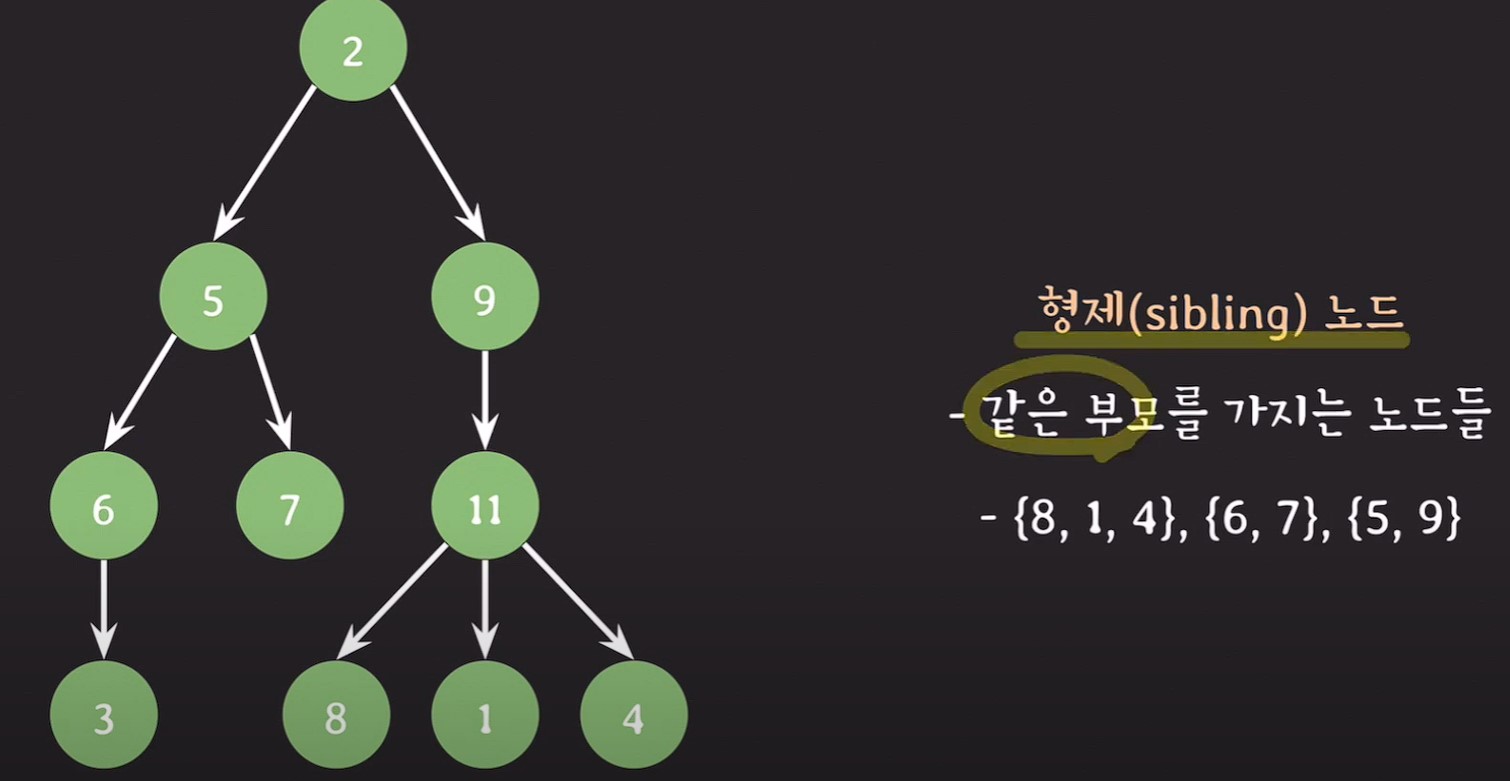
형제노드(sibling node) : 같은 부모를 가지는 노드들
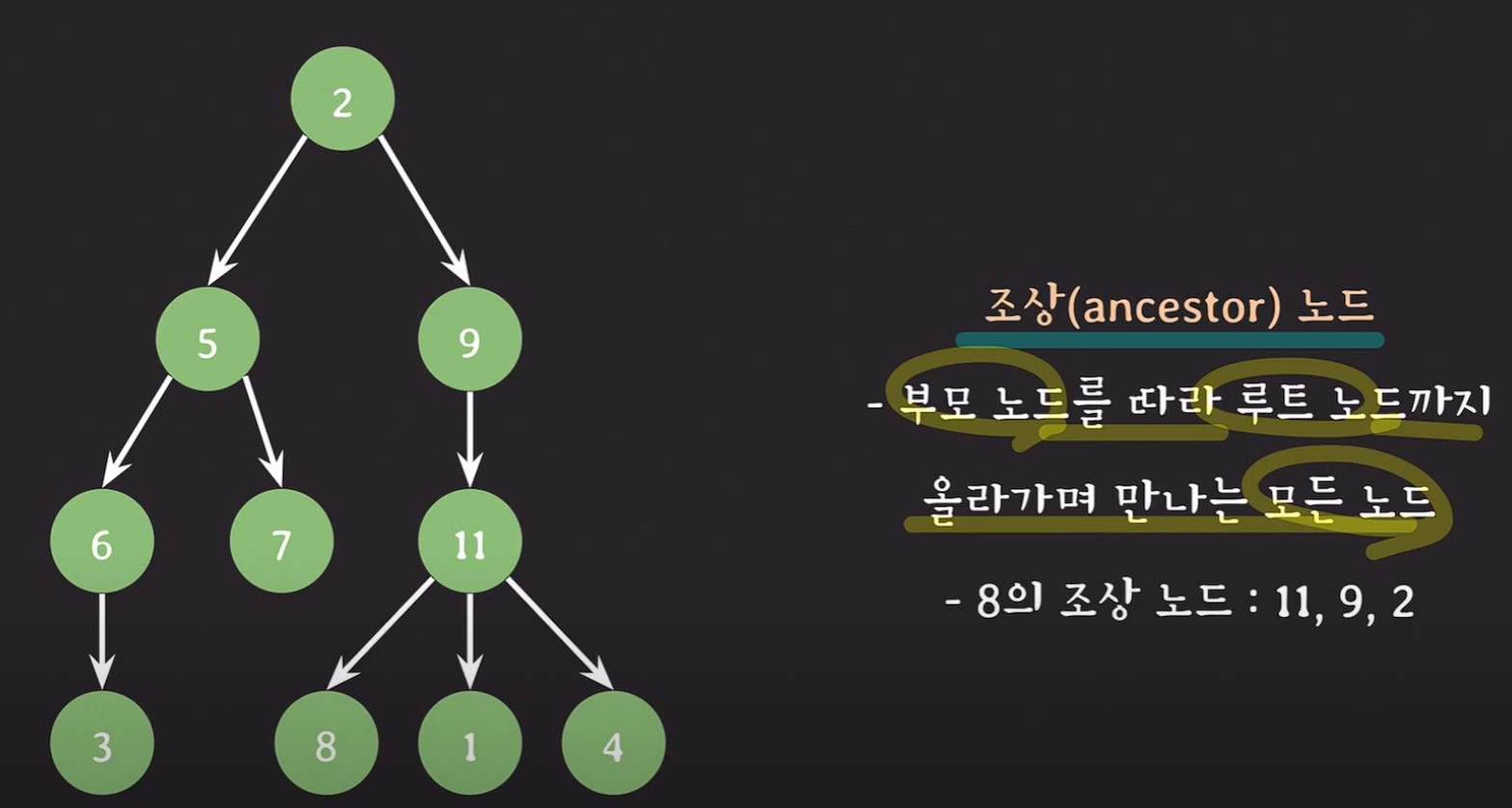
조상노드(ancester node) : 부모노드를 따라 루트노드까지 올라가며 만나는 노드
ex) 3의 조상 노드 => 6, 5, 2
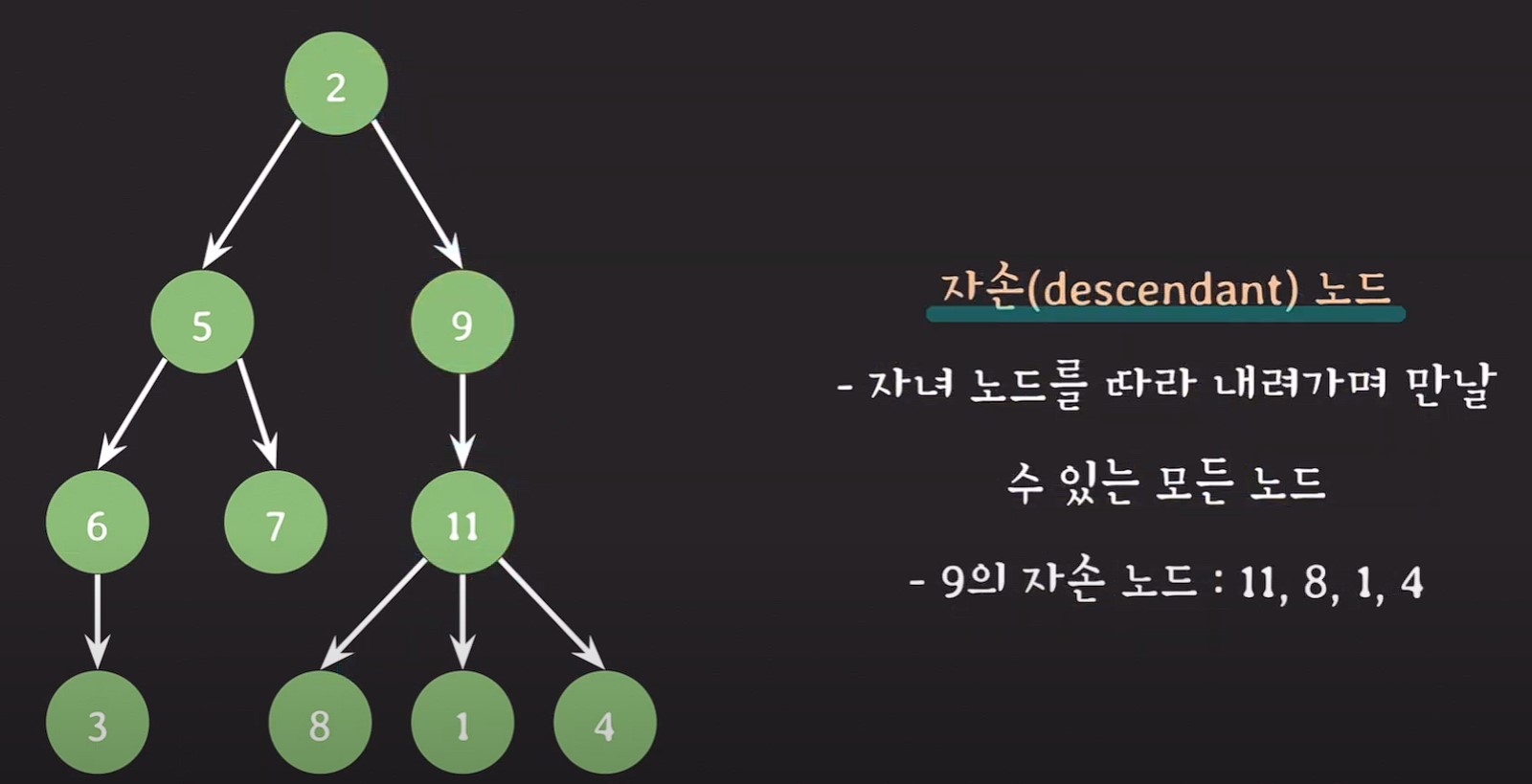
자손노드(descendant node) : 자녀노드를 따라 내려가며 만날 수 있는 모든 노드
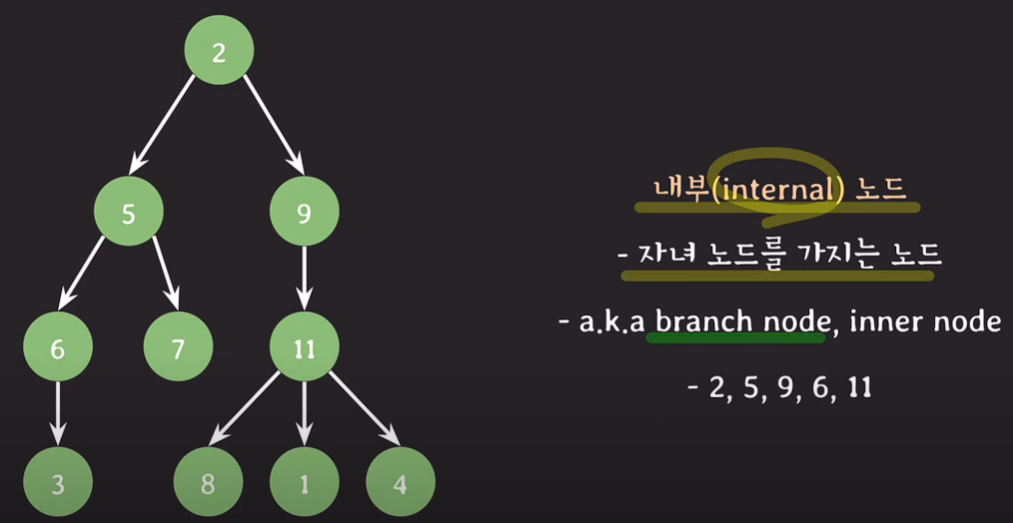
내부노드(internal node) : 자녀 노드를 가지는 노드
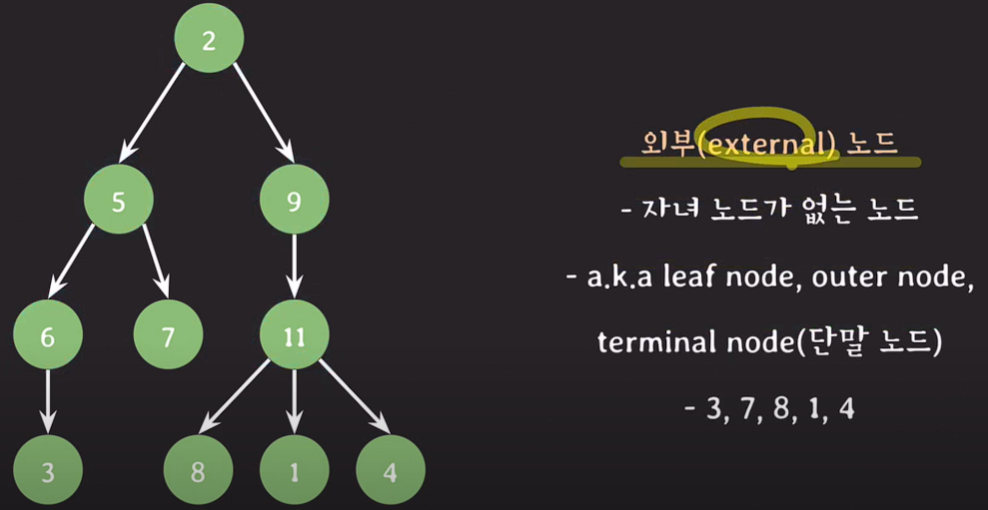
외부노드(external node,leaf node) : 자녀 노드가 없는 노드
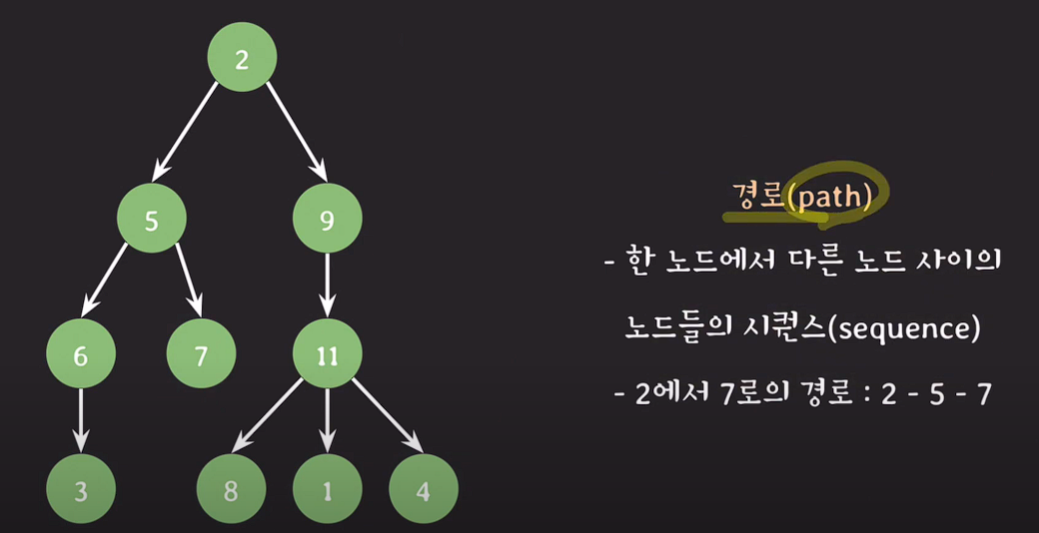
경로(path) : 한 노드에서 다른 노드 사이의 노드들의 시퀀스(sequence)
ex)2에서 4로의 경로 : 2-9-11-4
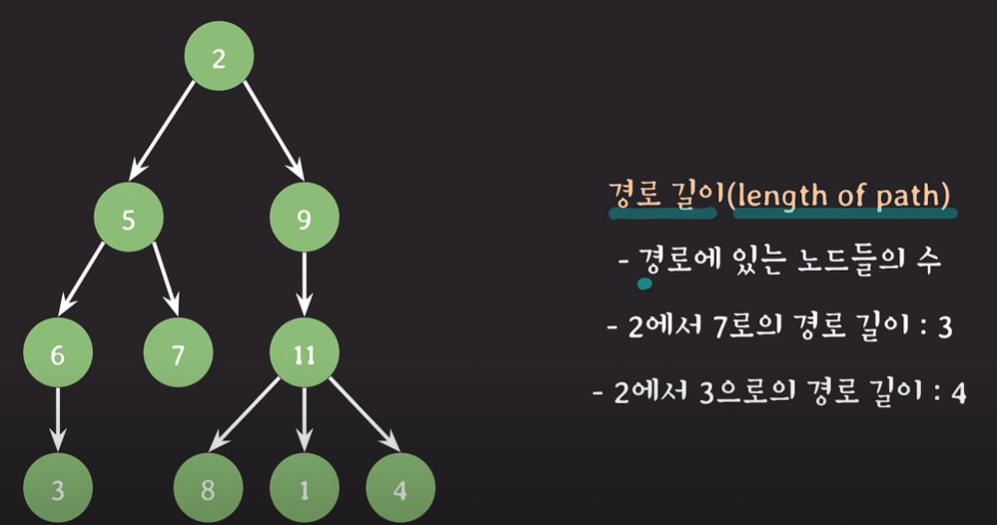
경로 길이(length of path) : 경로에 있는 노드들의 수
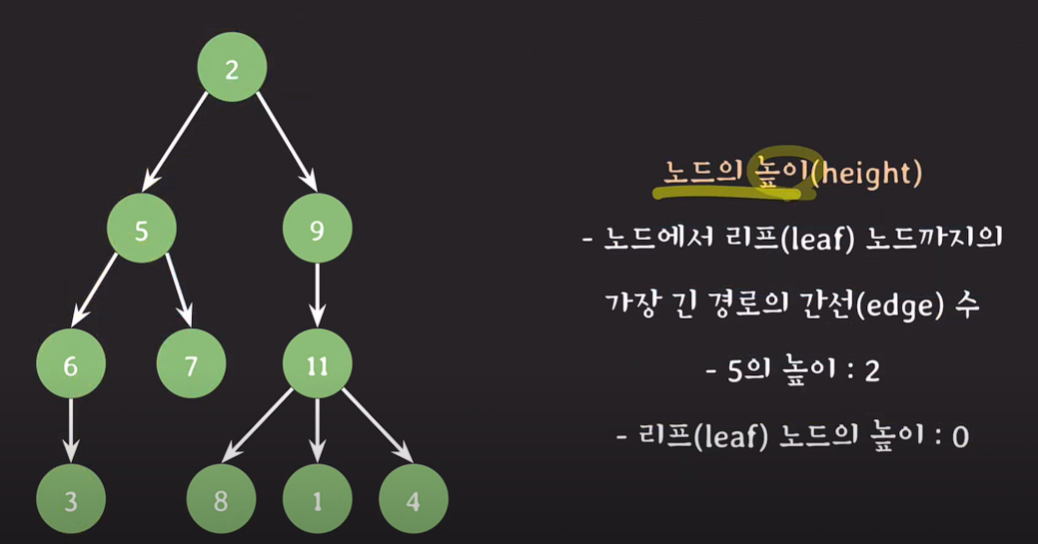
노드의 높이(height) : 노드에서 자기 자손의 리프(leaf)노드 까지의 가장 긴 경로의 간선(edge) 수
ex)노드 9의 높이 : 2
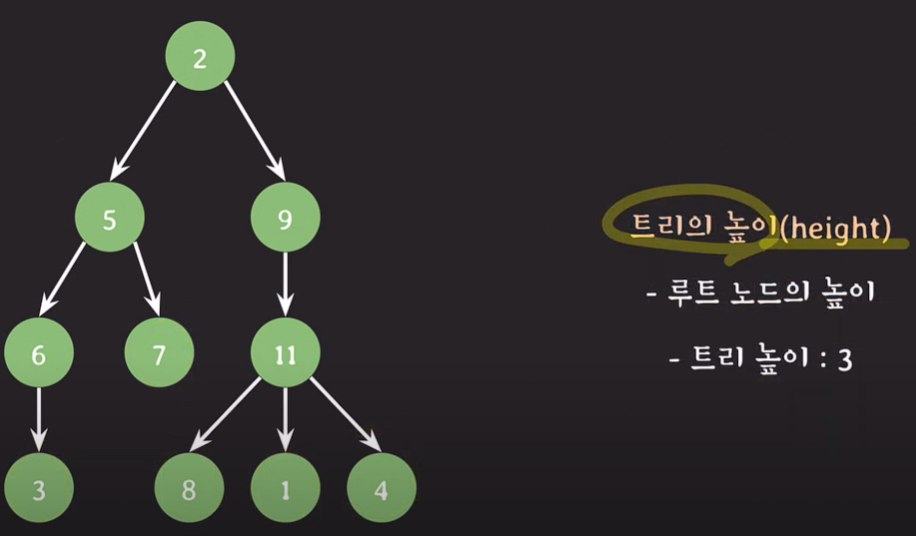
트리의 높이 : 루트 노드의 높이, 루트 노트에서부터 리프노드 까지의 간선 수
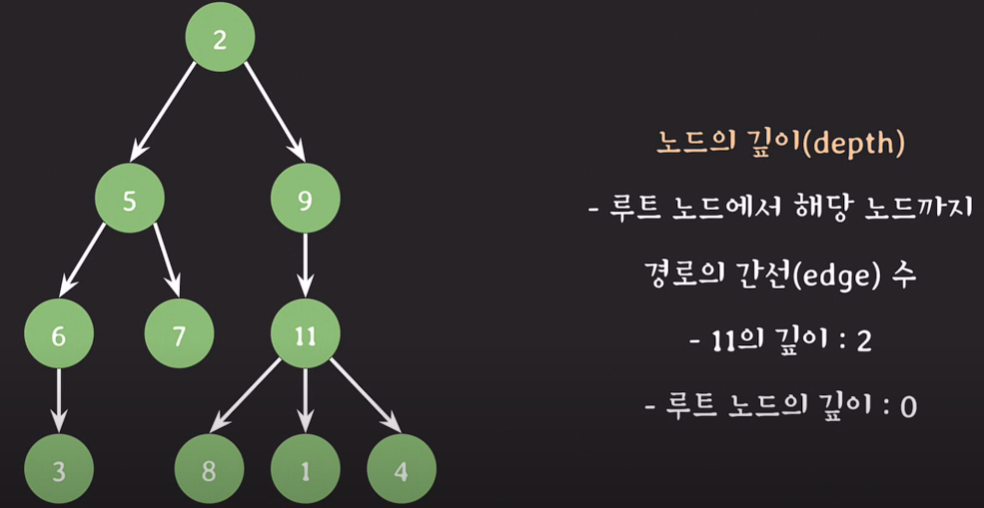
노드의 깊이(depth) : 루트 노드에서 해당 노드까지 경로의 간선 수
ex) 11의 깊이 = 2, 11의 높이 = 1, 3의 깊이 = 3
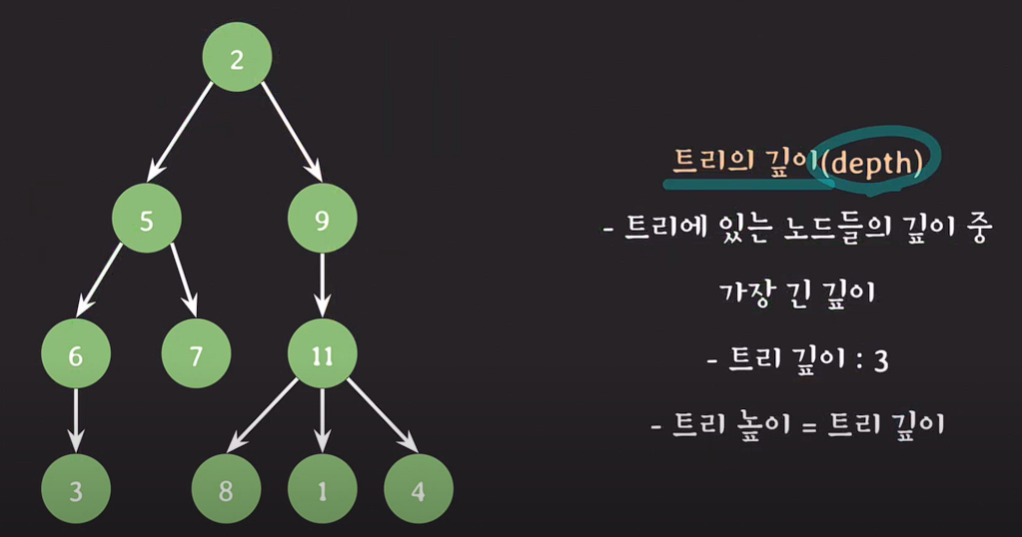
트리의 깊이 : 트리에 있는 노드들의 깊이 중 가장 긴 깊이
트리의 깊이 = 트리의 높이
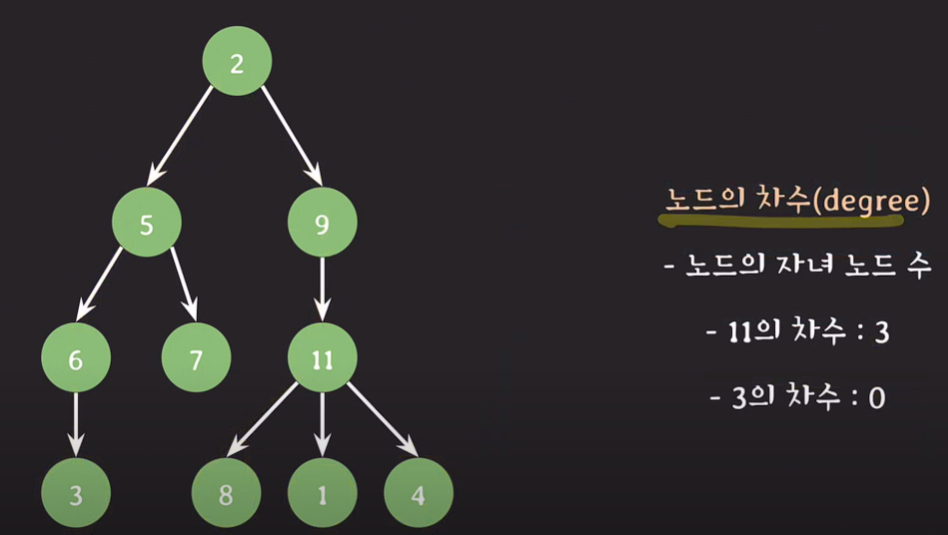
노드의 차수(degree) : 노드의 자녀 노드 수, 자손 노드는 포함하지 않는다.
ex)9의 차수 : 1
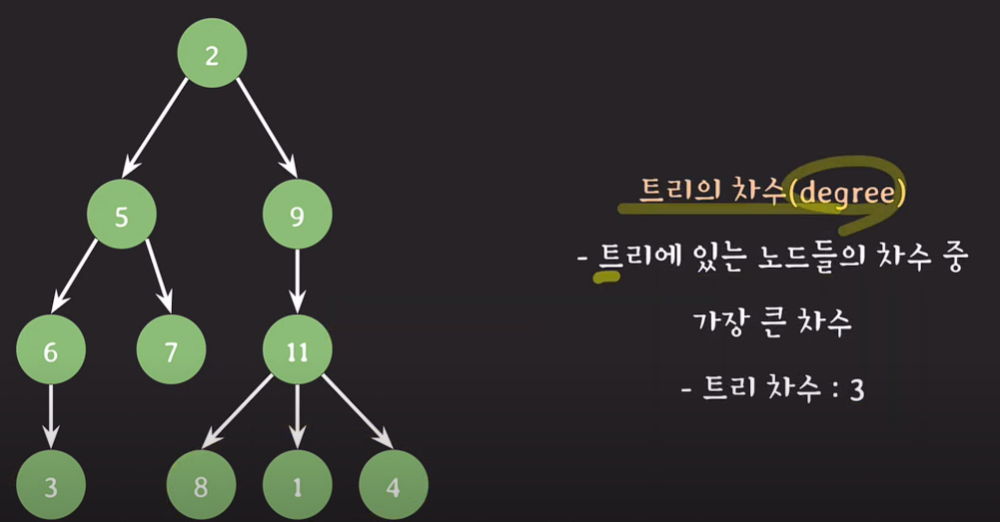
트리의 차수 : 트리에 있는 노드들의 차수 중 가장 큰 차수
ex)11의 차수 3이 트리의 차수이다.
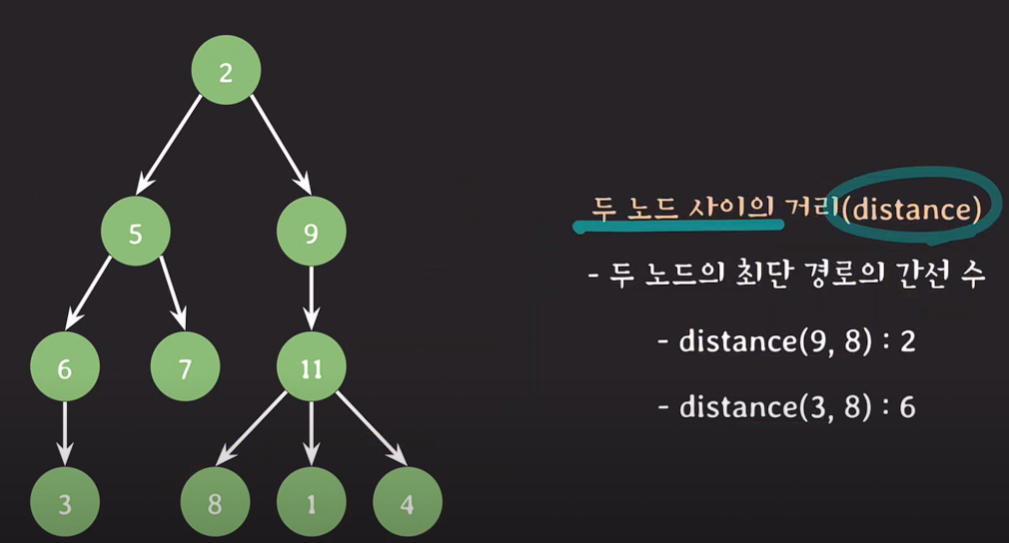
두 노드 사이의 거리(distance) : 두 노드의 최단 경로의 간선 수
ex)distance(3,2) : 3, distance(4,7) : 5
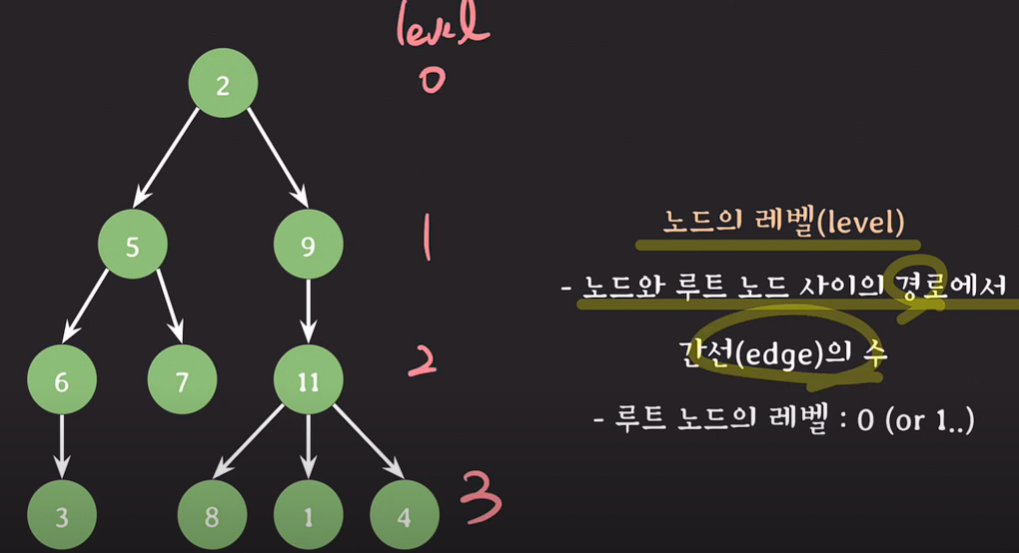
노드의 레벨(level) : 노드와 루트 노드 사이의 경로에서 간선의 수
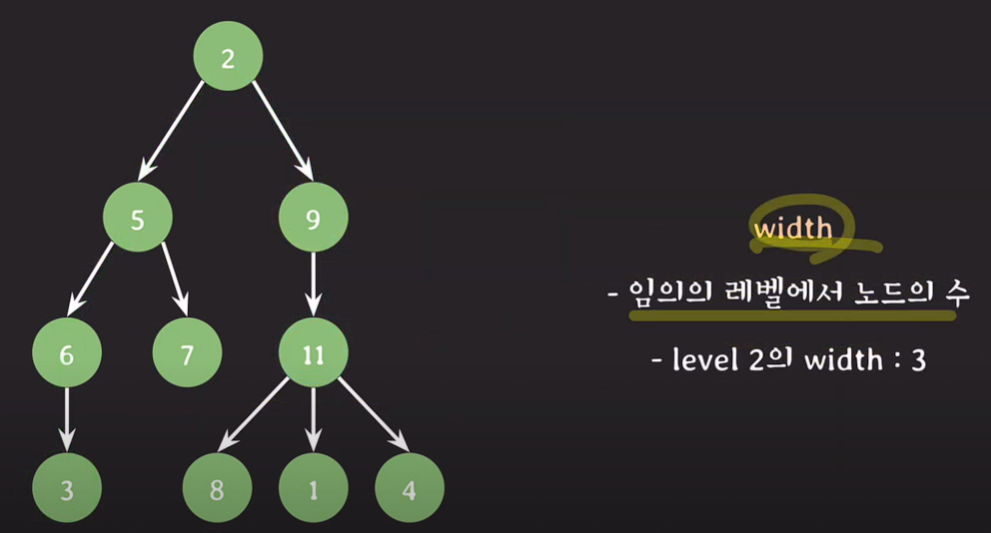
width : 임의의 레벨에서 노드의 수
ex)level 3의 width : 4
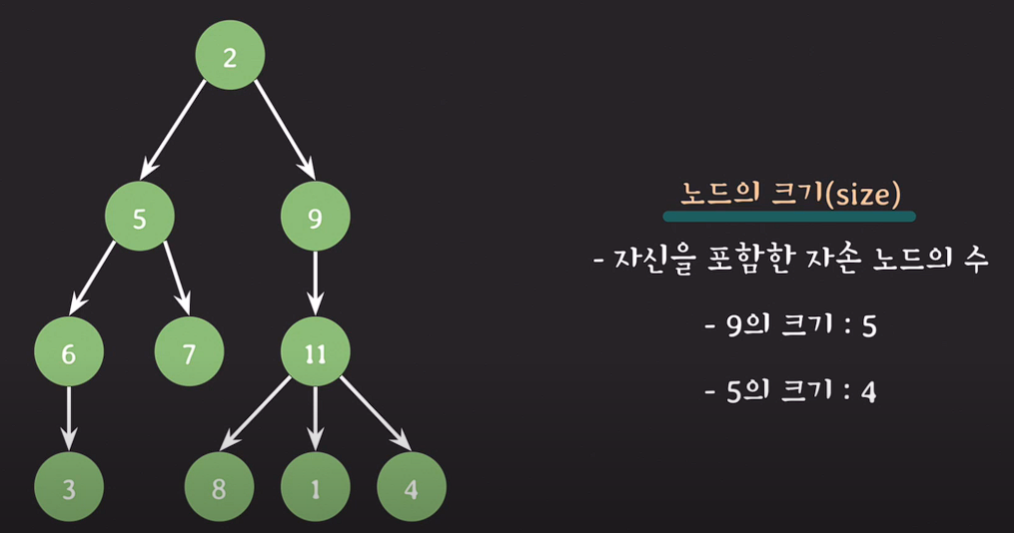
노드의 크기(size) : 자신을 포한한 자손 노드의 수
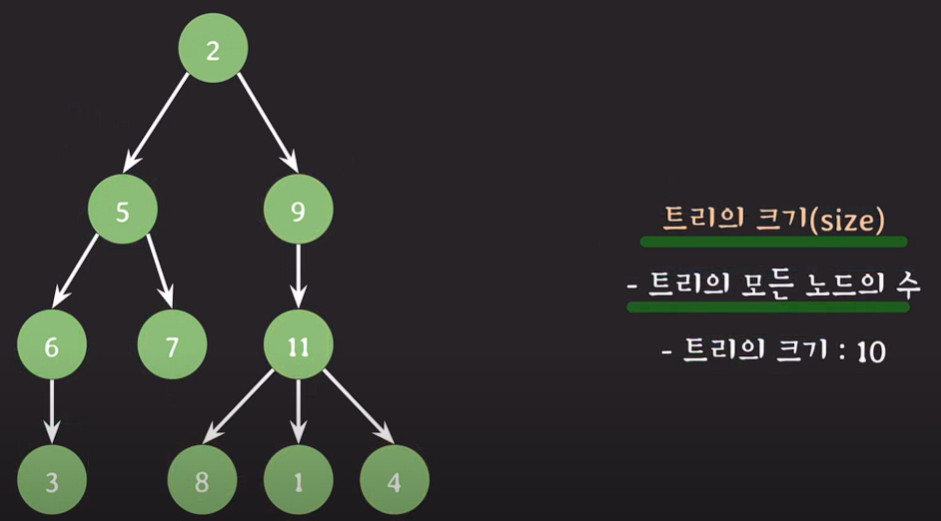
트리의 크기 : 트리의 모든 노드의 수
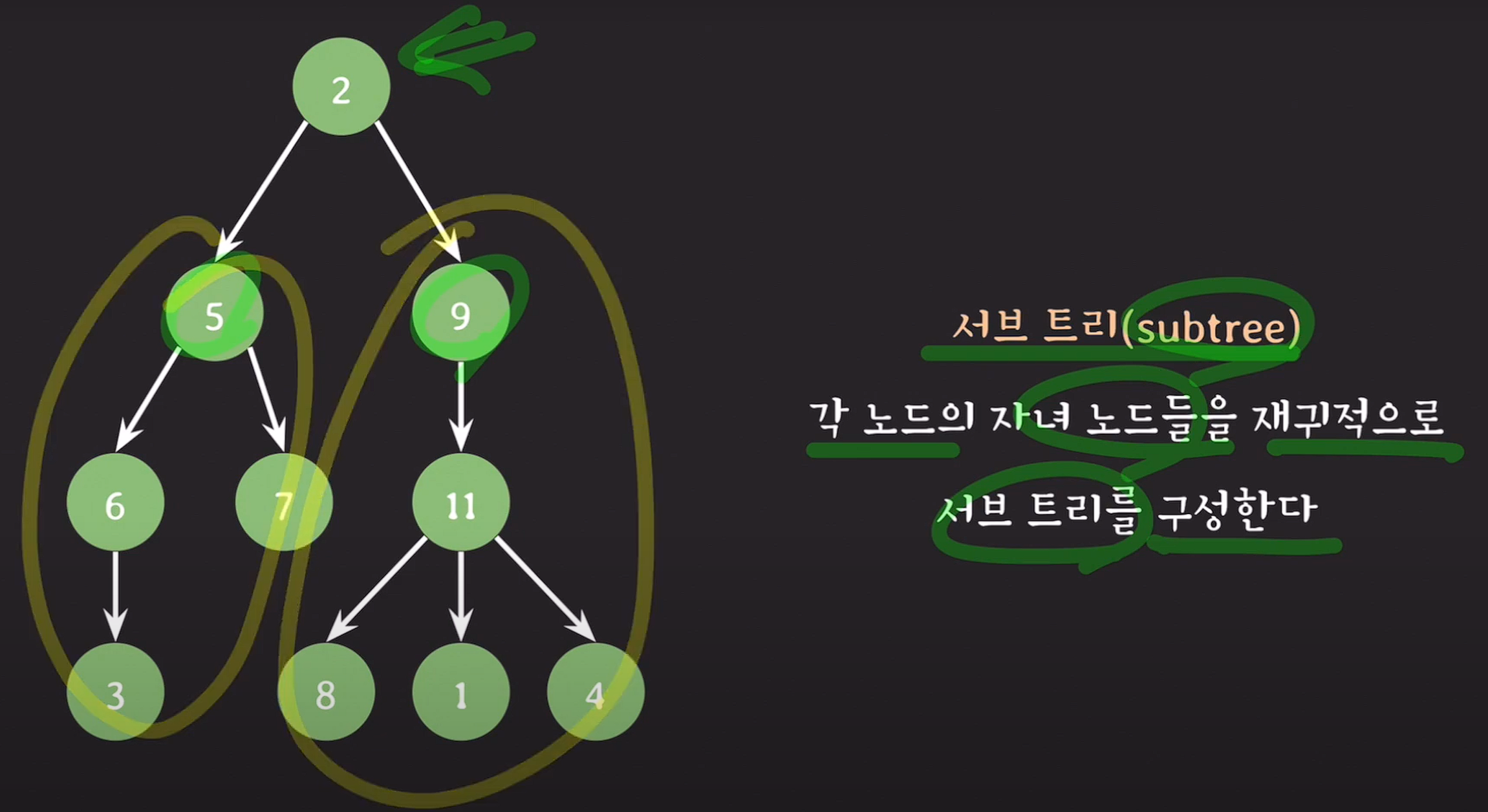
서브 트리(subtree) : 각 노드의 자녀노드들을 재귀적으로 서브 트리를 구성한다.
트리구조의 주요 특징

트리가 아닌경우 :
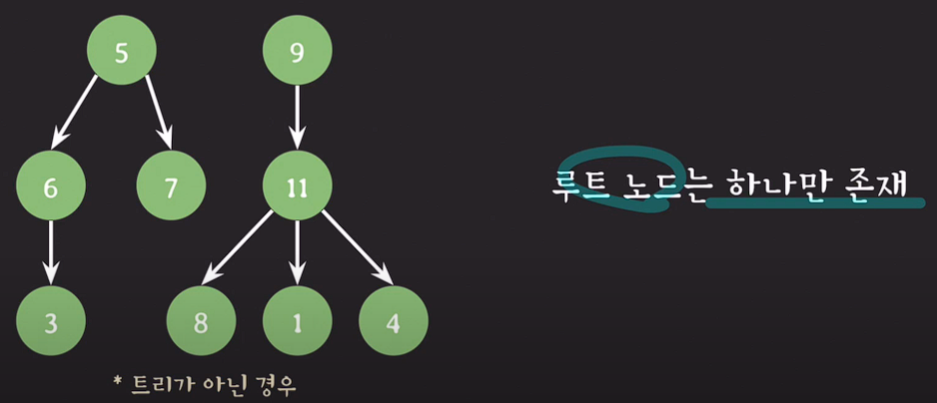
루트 노드는 반드시 하나만 존재한다.
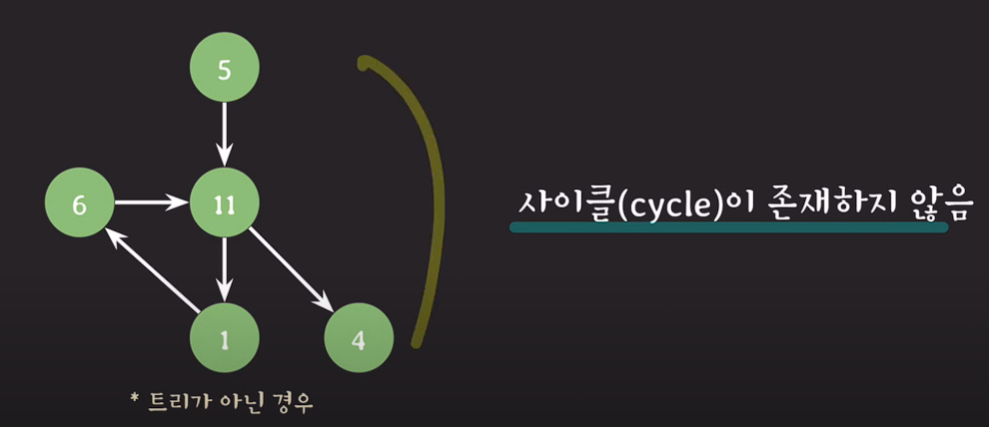
트리는 사이클이 존재하지 않는다.
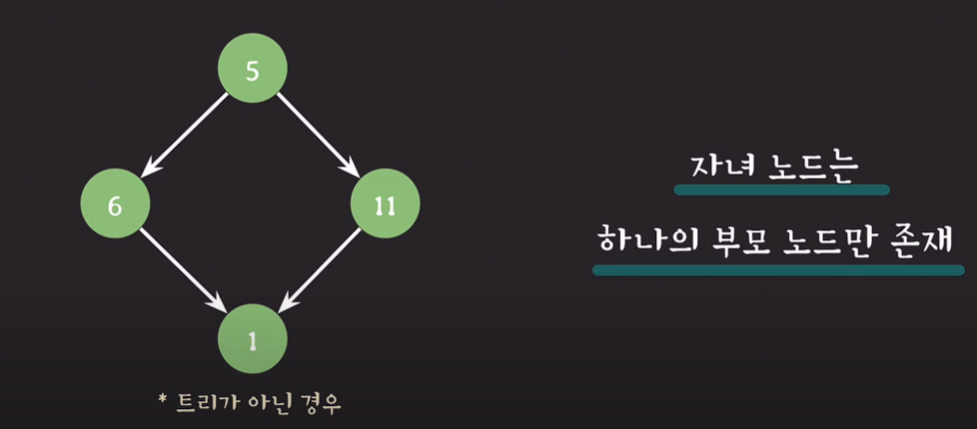
자녀 노드는 하나의 부모 노드만 존재한다.
트리의 구조

- 데이터를 순차적으로 저장하지 않는 비선형 구조
- 트리에 서브 트리가 있는 재귀적 구조
- 계층적 구조
Binary Tree

이진트리의 정의
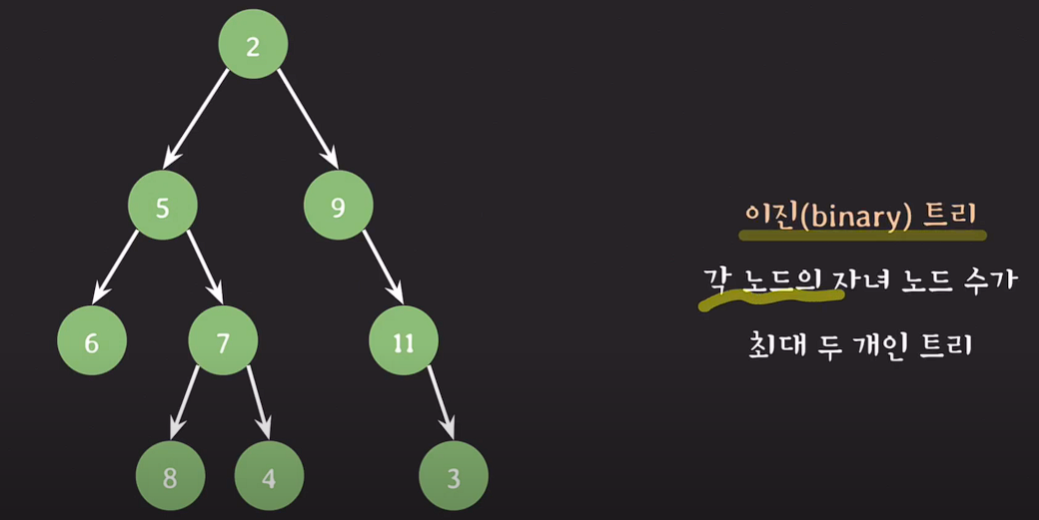
각 노드의 자녀 노드 수가 최대 두 개인 트리(0~2개)
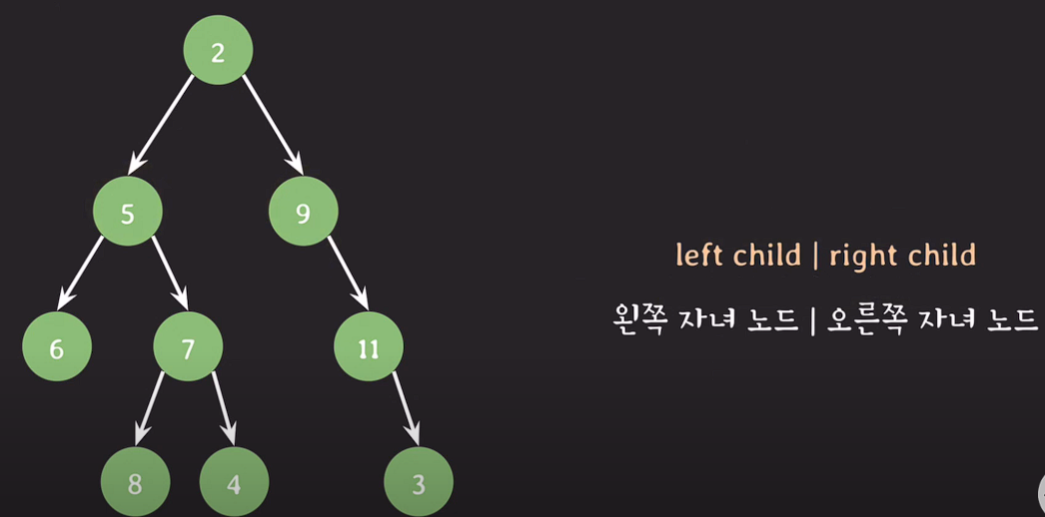
형태에 따른 이진트리의 종류

full binary tree
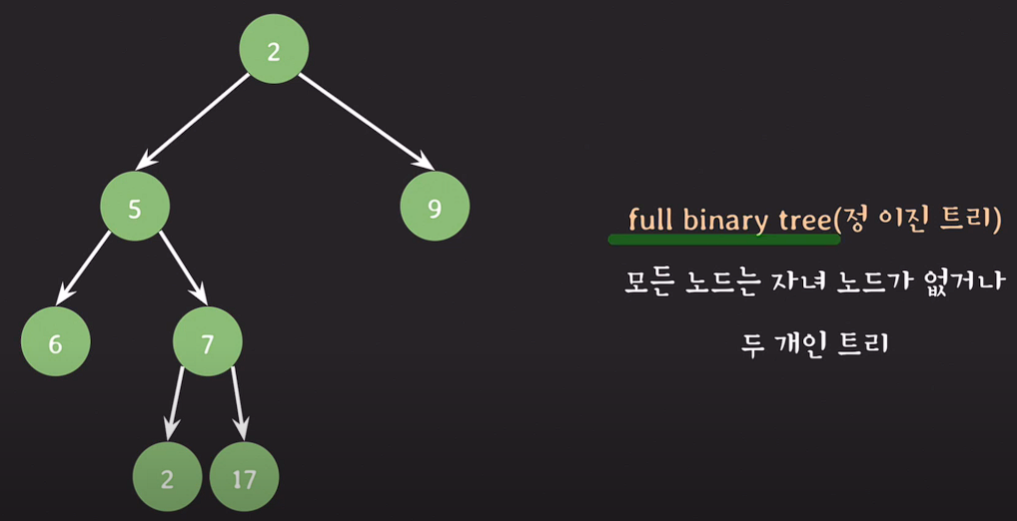
정 이진트리 : 모든 노드는 자녀 노드가 없거나 두개인 트리(0 or 2)
즉, 자녀 노드가 한개인 노드는 존재하지 않는다.
complete binary tree
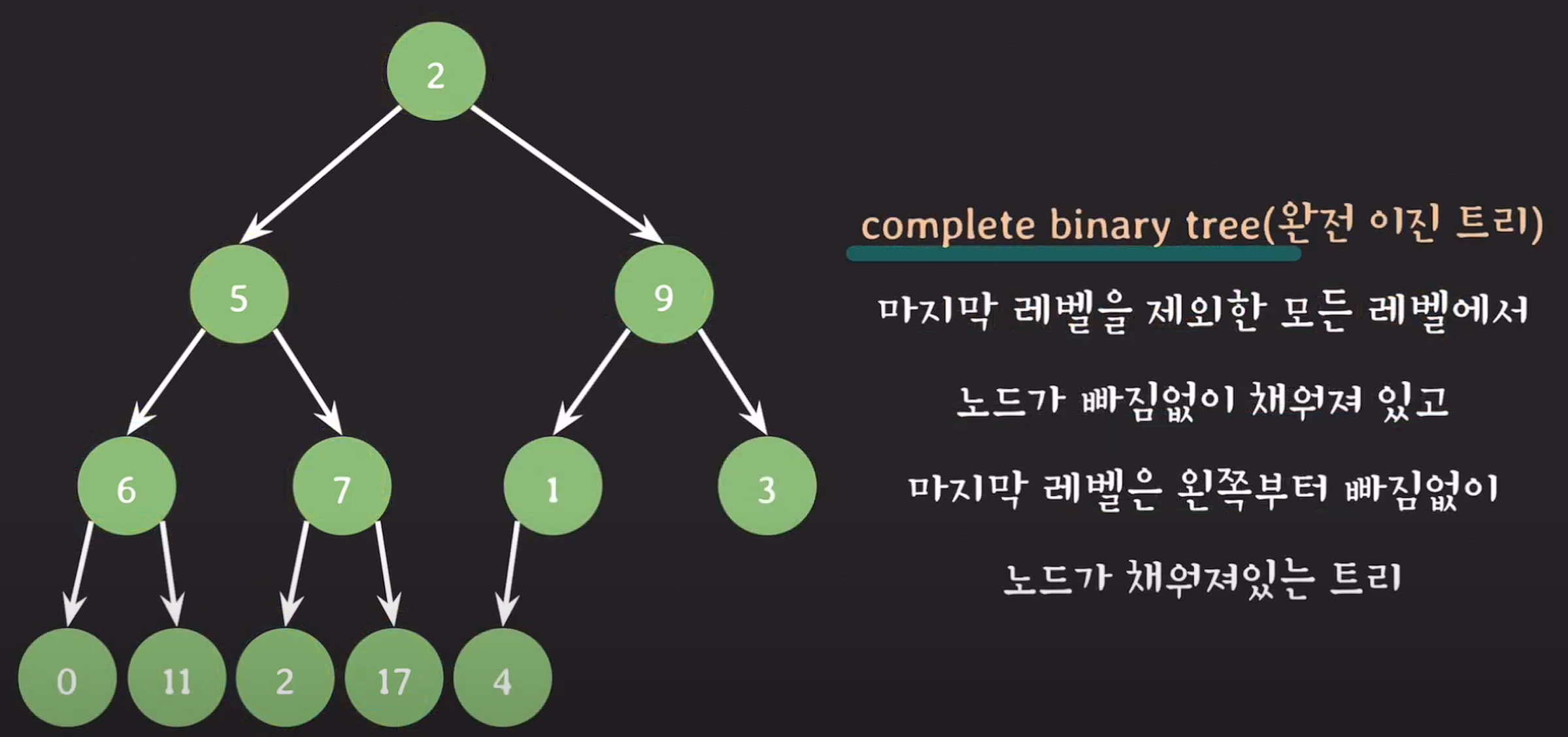
완전 이진 트리 : 마지막 레벨을 제외한 모든 레벨에서 노드가 빠짐없이 채워져 있고, 마지막 레벨은 왼쪽부터 빠짐없이 노드가 채워져있는 트리
ex) level3의 트리를 제외하고 모든 레벨의 트리는 노드가 빠짐없이 채워져있고,
level3의 왼쪽부터 노드가 추가된다.
perfect binary tree
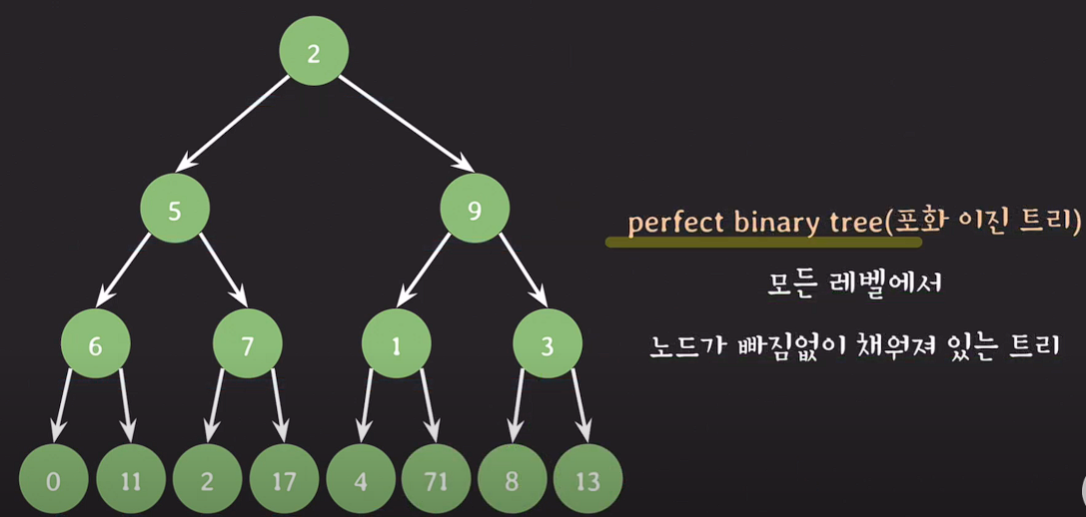
포화 이진 트리 : 모든 레벨에서 노드가 빠짐없이 채워져 있는 트리
degenerate binary tree
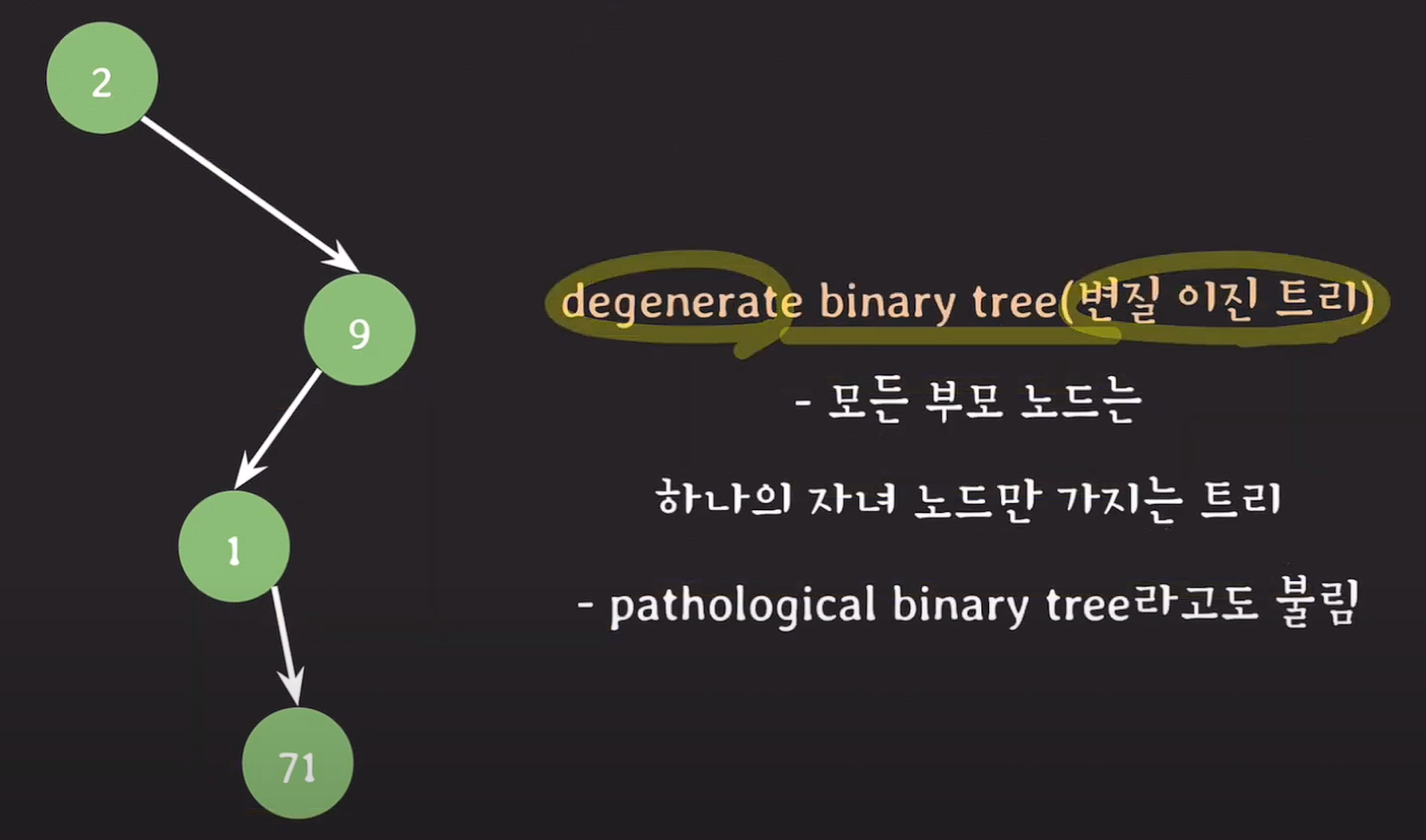
변질 이진 트리 : 모든 부모 노드는 하나의 자녀 노드만 가지는 트리

왼쪽 변질 트리 : 모든 부모 노드는 왼쪽 자녀 노드만 가지는 트리
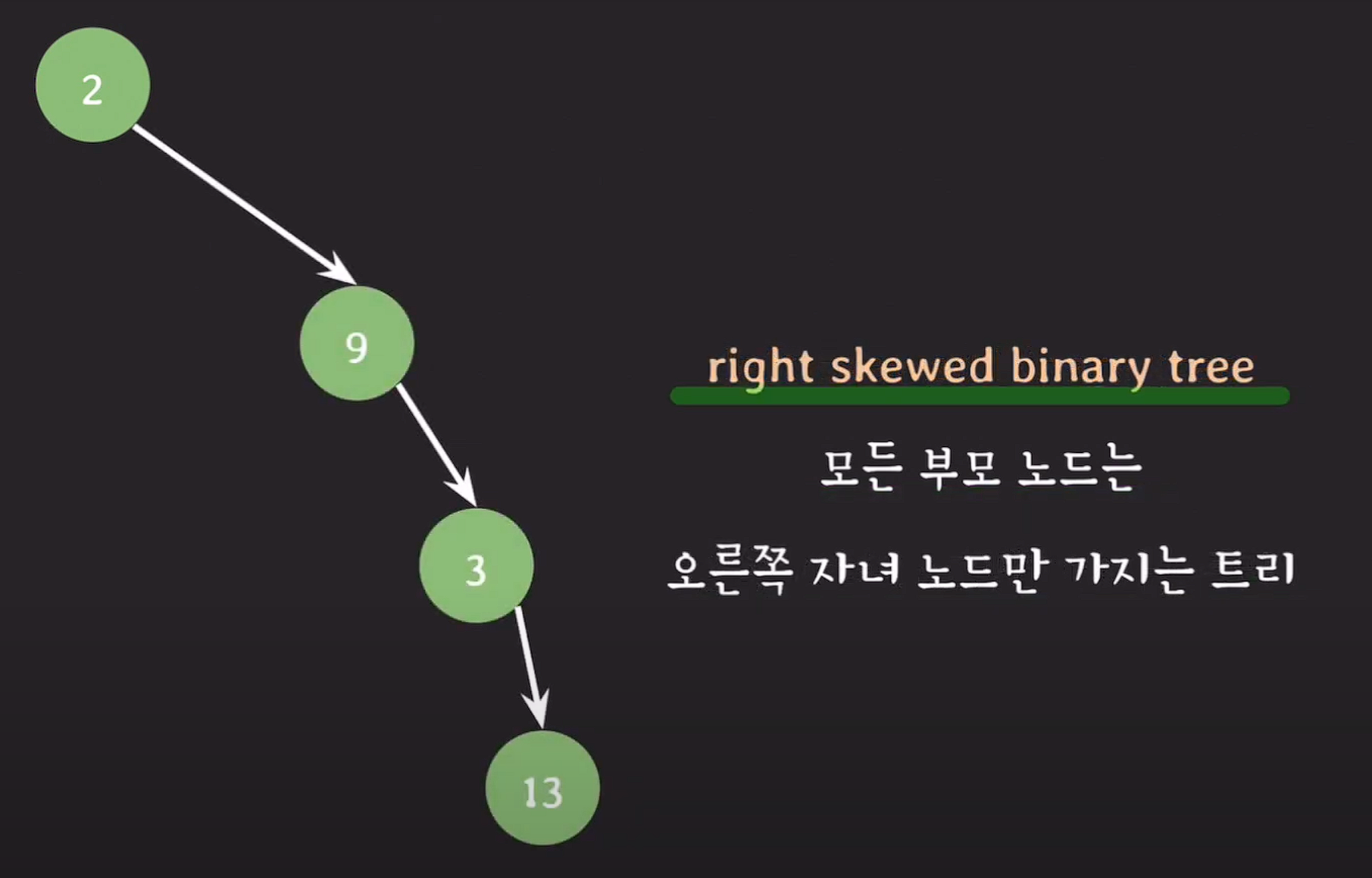
오른쪽 변질 트리 : 모든 부모 노드는 오른쪽 자녀 노드만 가지는 트리
blanced binary tree
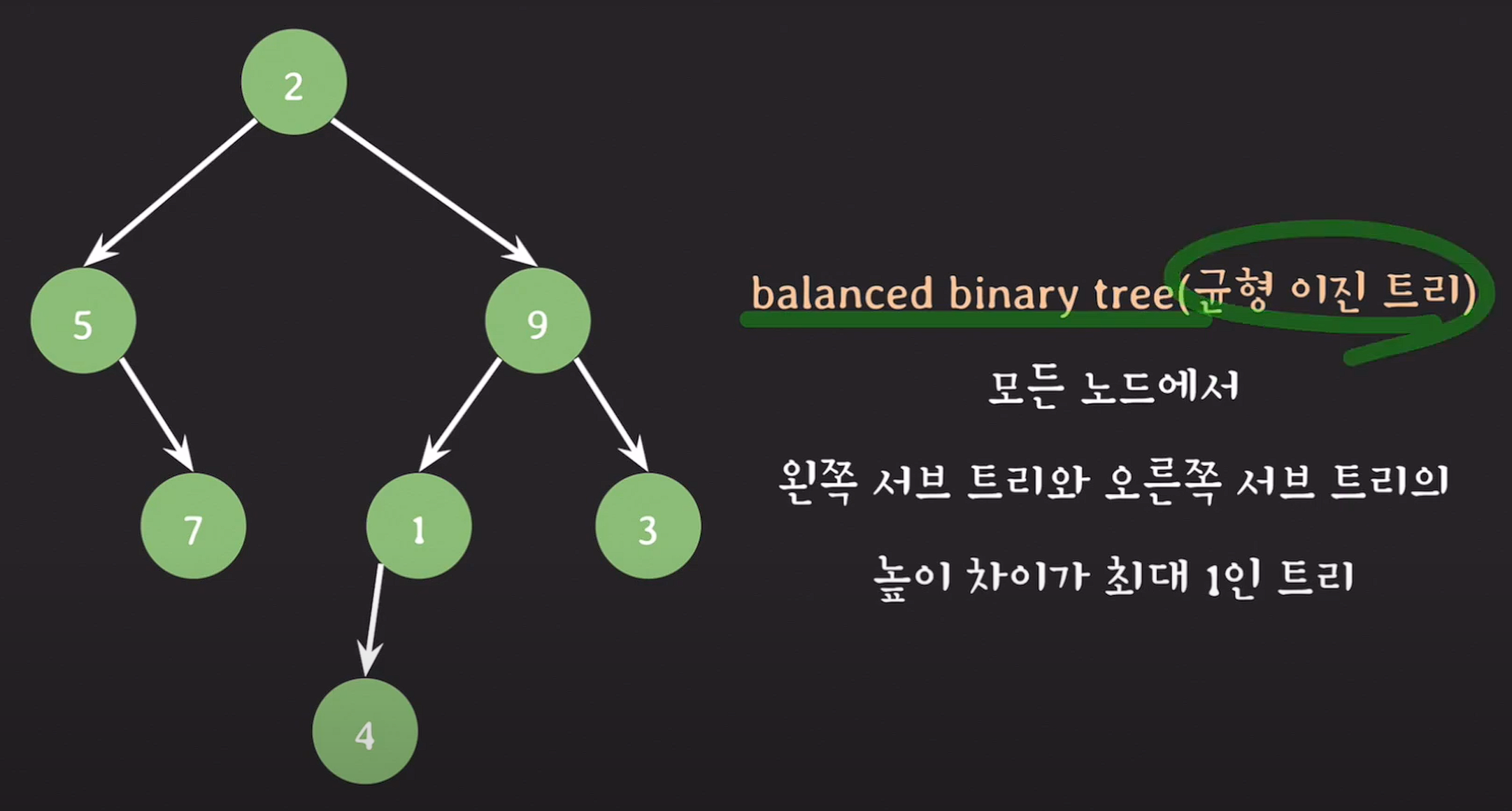
균형 이진 트리 :
모든 노드에서 왼쪽 서브트리와 오른쪽 서브 트리의 높이 차이가 최대 1인 트리
이진트리의 높이에서 한쪽의 자손노드가 존재하는데 다른 쪽의 자손노드가 없는 경우 높이는 -1이다. 자손이 아에 없는 리프 노드 양쪽이 0.
ex) 2번 노드 기준 5의 높이 1, 9의 높이 2 => 1차이
5번 노드 기준 왼쪽 -1, 7의 높이 0 => 1차이
9번 노드 기준 왼쪽 1, 오른쪽3 => 1차이
1번 노드 기준 왼쪽 0, 오른쪽 -1 => 1차이