LCS

문제

---

ACAYKP
CAPCAK

---

위의 예시는 ACAK가 순서대로 겹치는 경우가 가장 긴 부분수열이다

따라서 답은 4

설명

2차원 dp 문제

		C	A	P	C	A	K
	0	0	0	0	0	0	0
A	0	0	1	1	1	1	1
C	0	1	1	1	2	2	2
A	0	1	2	2	2	3	3
Y	0	1	2	2	2	3	3
K	0	1	2	2	2	3	4
P	0	1	2	3	3	3	4

2차원 dp배열의 행, 열은 비교할 두 문자열의 알파벳이 각각 해당하게 된다.
위치가 dp[i][j]라 가정할 때, 이 칸은 첫번째 문자열 i까지와 두번째 문자열 j까지 비교했을 때 가장 긴 부분수열을 의미한다.

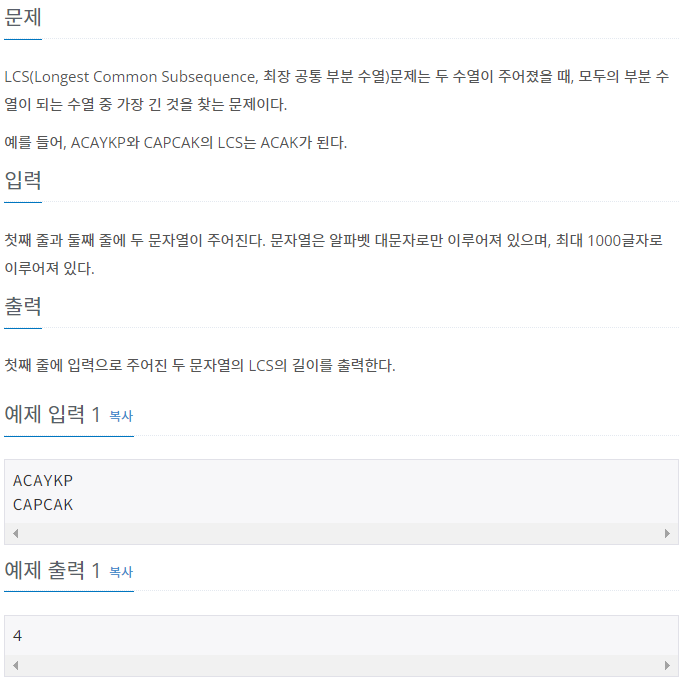
• 칸의 두 알파벳이 동일한 경우
  예시로 아래의 그림과 같이 ACA와 CA를 비교했을 때 최대 길이는 AC와 CA를 비교했을 때 최대길이 + 1 이 된다
  점화식 : dp[i][j] = dp[i-1][j-1]+1
  

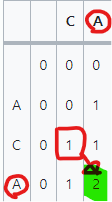
• 칸의 두 알파벳이 다른 경우
  예시로 CAP와 AC를 비교했을 때 맨 끝의 알파벳 P와 C는 다르므로 CAP와 A를 비교했을 때 최대 부분수열 길이, CA와 AC를 비교했을 때의 최대 부분수열 길이 중 큰 수를 택해서 가져온다.
  점화식 : dp[i][j] = max(dp[i][j-1],dp[i-1][j])
  

if(arr1[i-1]==arr2[j-1]){  
			 	map[i][j] = map[i-1][j-1]+1;
			}else{ 
			 	map[i][j] =  max(map[i-1][j],map[i][j-1]);
			}		

코드

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
char arr1[1001];
char arr2[1001];
int map[1001][1001];
int main(){
	scanf("%s",arr1);
	scanf("%s",arr2);
	int len1 = strlen(arr1); // 미리 저장하지 않고 바로 반복문에 사용하면  
	int len2 = strlen(arr2); // 시간초과가 나는 경우도 있다... 
	
	for(int i=1;i<=len1;i++){
		for(int j=1;j<=len2;j++){
			 if(arr1[i-1]==arr2[j-1]){ // 두 알파벳이 같다면  
			 	map[i][j] = map[i-1][j-1]+1;
			 }else{ // 두 알파벳이 다르다면  
			 	map[i][j] =  max(map[i-1][j],map[i][j-1]); // <algorithm> 헤더에 내장돼있는 max 함수 사용
			 }
		} 
	}
	printf("%d",map[len1][len2]);
	
}