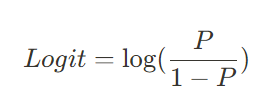ML PYTHON CLASS#3

codataffee·2024년 6월 7일

python

PYTHON CLASS

목록 보기

10/16

개요

머신러닝의 기본 정의 및 종류

📌 3회차 요약

분류 분석 > 로지스틱 회귀

📌 로지스틱 회귀

📌 개념

타이타닉 생존 분류 문제

Kaggle 타이타닉 예측 대회

# 라이브러리 불러오기
import sklearn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 데이터 조회
# 가설 : 비상 상황 특성상 여성을 배려해 여성이 많이 생존했을 것이다.
    # pivot table 을 만들어 확인
    # 그래프를 그려 확인

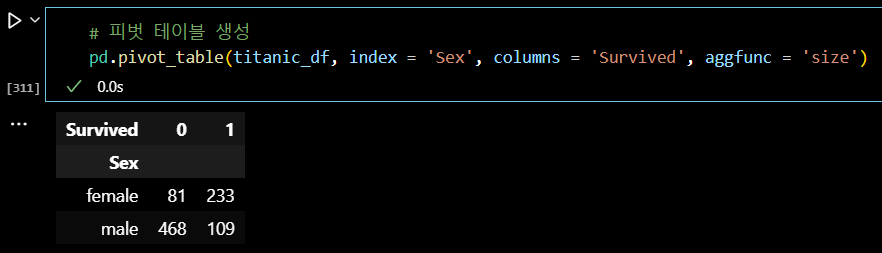
# 피벗 테이블 생성
pd.pivot_table(titanic_df, index = 'Sex', columns = 'Survived', aggfunc = 'size')

len(titanic_df) # 891
# 정확도 (Accuracy) : 맞춘 갯수 / 전체 데이터
# 생존을 맞춤 ; 여성은 전부 생존, 남성은 전부 사망
(233 + 468) / 891 * 100 # 78.68

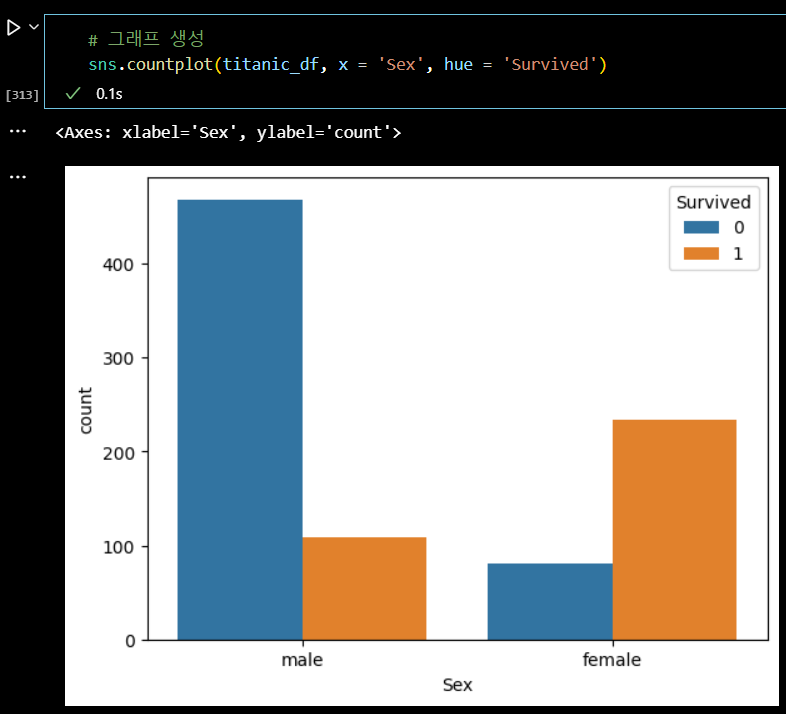
# 그래프 생성
sns.countplot(titanic_df, x = 'Sex', hue = 'Survived')

📌 이론

범주형 Y 에서 선형함수의 한계

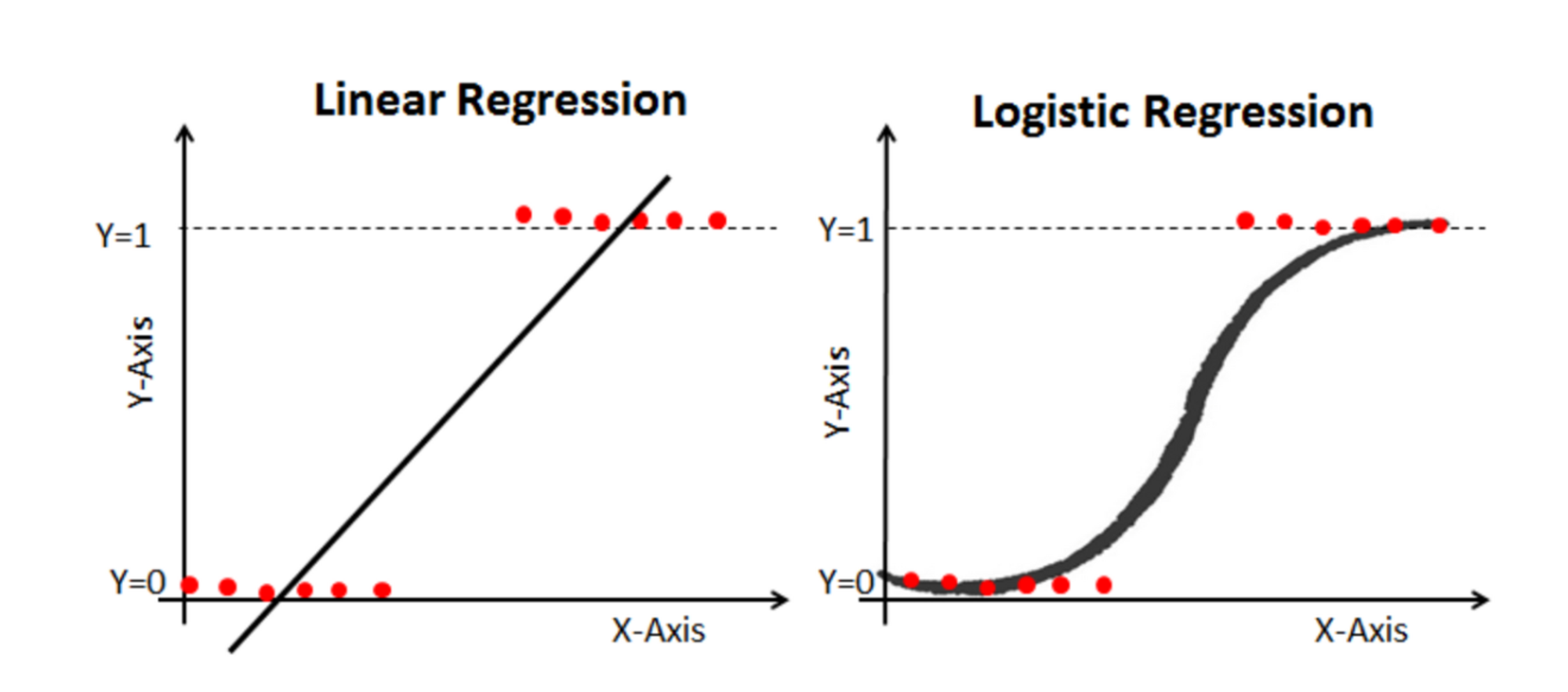
X가 연속형 변수이고, Y가 특정 값이 될 확률이라고 설정한다면,
왼쪽 그림과 같이 선형으로 설명하긴 쉽지 않다.
확률은 0과 1사이 인데, 예측 값이 확률 범위를 넘어갈 수 있는 문제가 발생하기 때문.
하지만 오른쪽 그림처럼 S자 형태의 함수를 적용하면 잘 설명한다고 할 수 있다.

로짓 개념의 등장

오즈비(odds ratio) : 승산비라고도 불리며, 실패확률 대비 성공확률을 의미

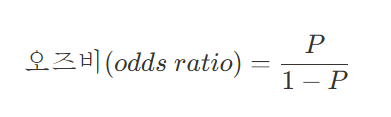
오즈비에서 P는 확률값으로 0 ~ 1 사이 값인데,
P 가 증가할수록 오즈비가 급격하게 증가하기 때문에
확률이 급격하게 증가하며 선형성을 따르지 않는 문제가 있다.

문제를 완화하기 위해 로그 씌우기

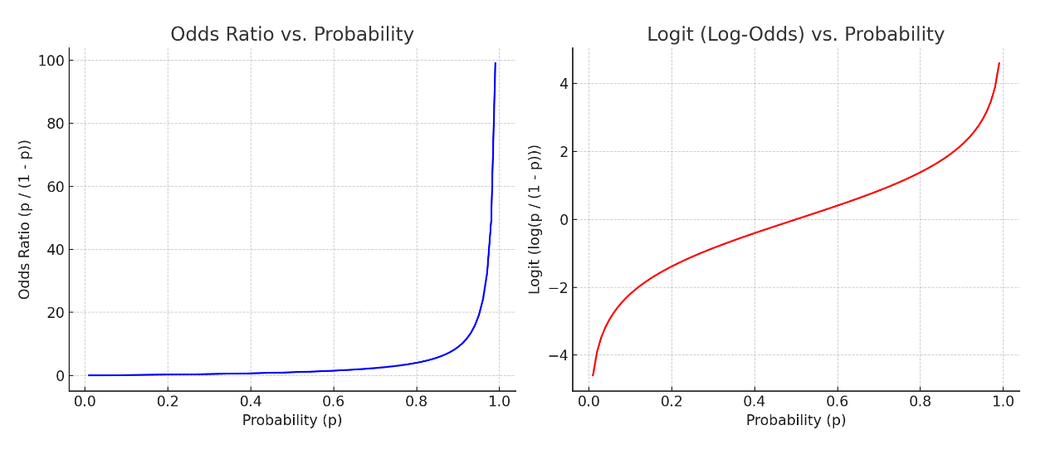
오즈비와 확률의 관계 / 로짓과 확률의 관계

로짓의 그래프가 더 선형적인 그림을 나타내 선형회귀의 기본식을 활용할 수 있다.
로지스틱 '회귀' 라고 불리는 이유.

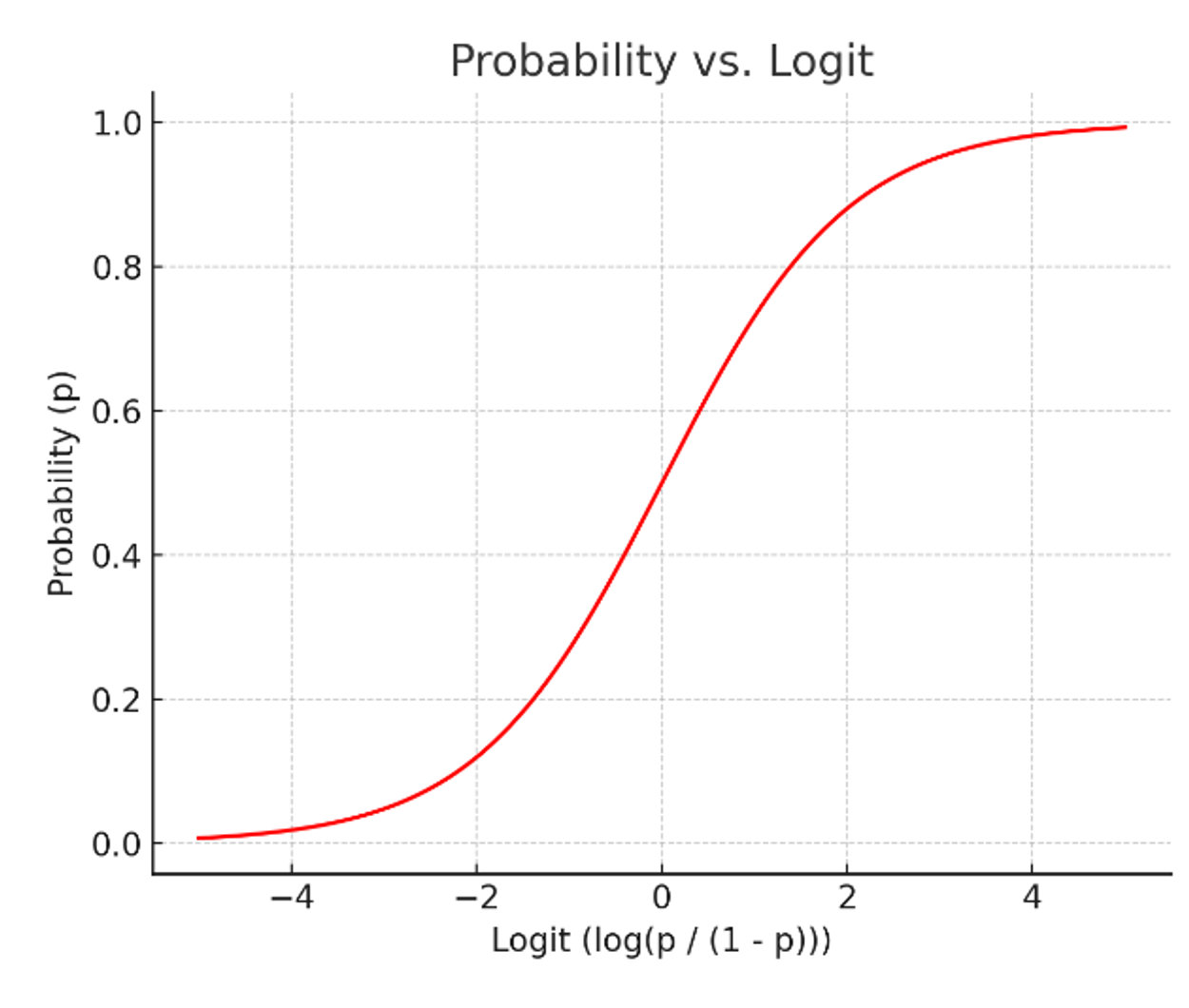
로지스틱 함수

로지스틱 함수는 시그모이드 함수 중 하나로 딥러닝에서 다시 활용, 값을 계산하면 확률이 도출

해석 : X 값이 ${w_1}$ 만큼 증가하면 오즈비는 $e^{w_1}$ 만큼 증가한다.

📌 분류 평가 지표

혼동 행렬 (Confusion Matrix) : 실제 값과 예측 값에 대한 모든 경우의 수를 표현하기 위한 2 * 2 행렬

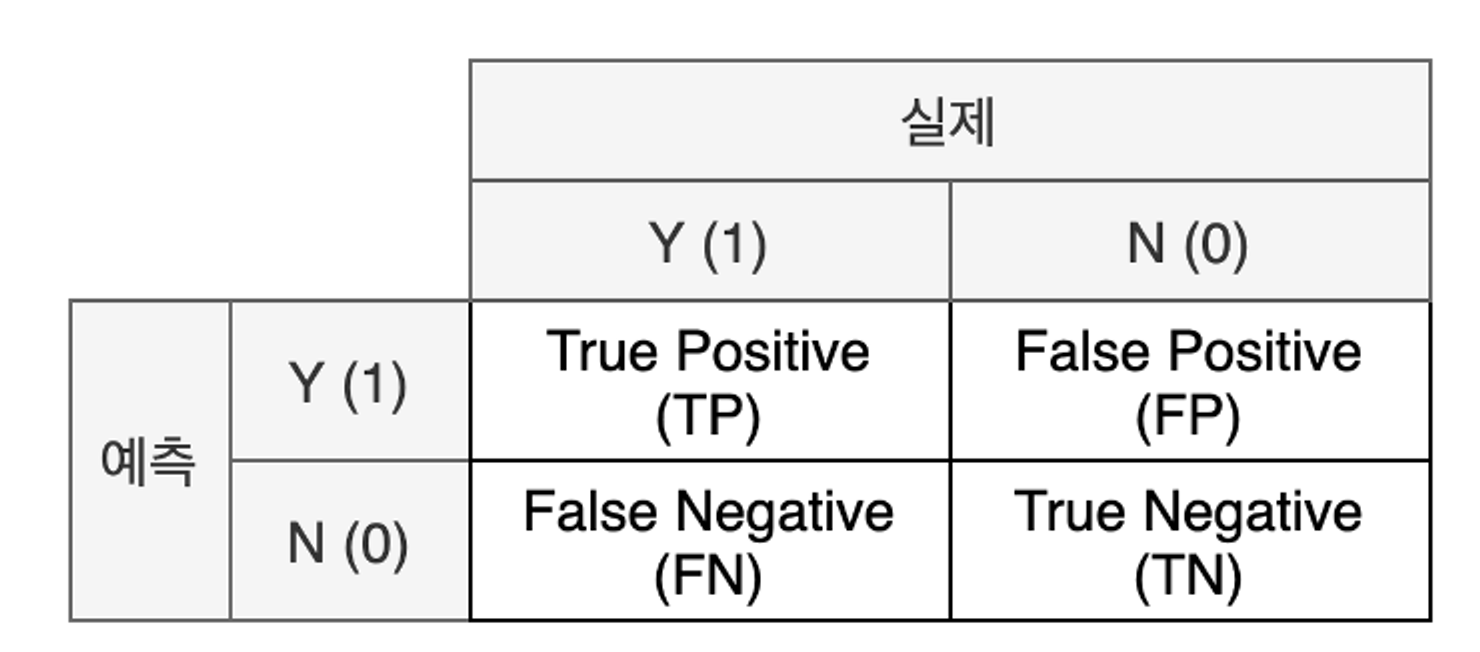
- 표기법
    - 실제와 예측이 같으면 True / 다르면 False
    - 예측을 양성으로 했으면 Positive / 음성으로 했으면 Negative
- 해석
    - TP: 실제로 양성(암 환자)이면서 양성(암 환자) 올바르게 분류된 수
    - FP: 실제로 음성(정상인)이지만 양성(암 환자)로 잘못 분류된 수
    - FN: 실제로 양성(암 환자)이지만 음성(정상인)로 잘못 분류된 수
    - TN: 실제로 음성(정상인)이면서 음성(정상인)로 올바르게 분류된 수

지표

정밀도 (Precision) : 모델이 양성 1로 예측한 결과 중 실제 양성의 비율 (모델 관점)
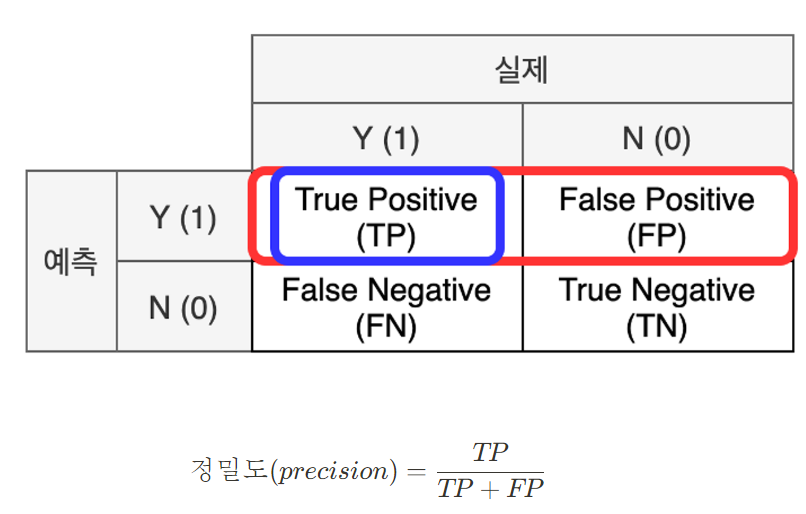
재현율 (Recall) : 실제 값이 양성인 데이터 중 모델이 양성으로 예측한 비율 (데이터 관점)
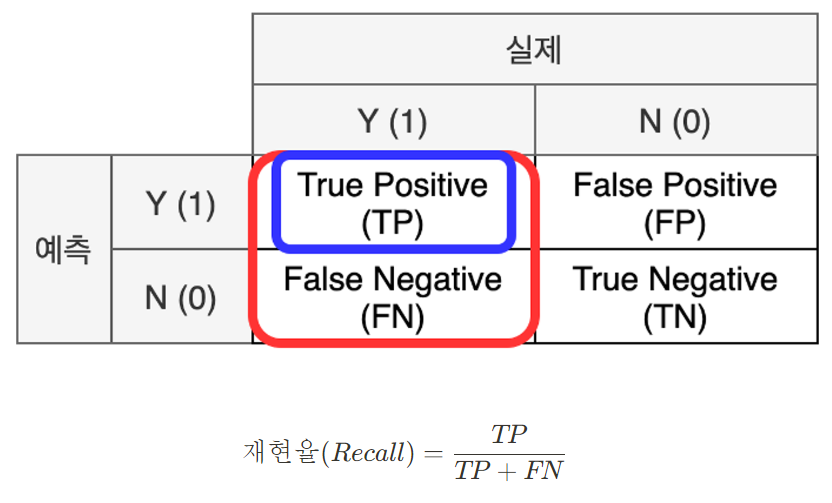
F1 - Score : 정밀도와 재현율의 조화 평균
정확도 (Accuracy) : 전체 데이터 중 모델이 예측에 성공한(양성, 음성) 비율

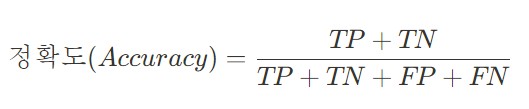
적용 (예시)
- TP: 실제로 양성(암 환자)이면서 양성(암 환자) 올바르게 분류된 수 → 0명
- FP: 실제로 음성(정상인)이지만 양성(암 환자)로 잘못 분류된 수 → 0명
- FN: 실제로 양성(암 환자)이지만 음성(정상인)이라고 분류된 수 → 5명
- TN: 실제로 음성(정상인)이면서 음성(정상인)이라고 분류된 수 → 95명
  - 정밀도는 정의되지 않음(divsion by zero), 재현율은 0
  - 결과적으로 f1-score는 0

정확도는 분류에서 Y 값이 밸런스하지 못할 때 제 기능을 하지 못한다.
따라서 Y 범주의 비율을 맞춰주거나 평가 지표를 F1 - Score 를 사용하며 보완한다.

📌 로지스틱 회귀 실습

# 데이터 확인
titanic_df.head(3)

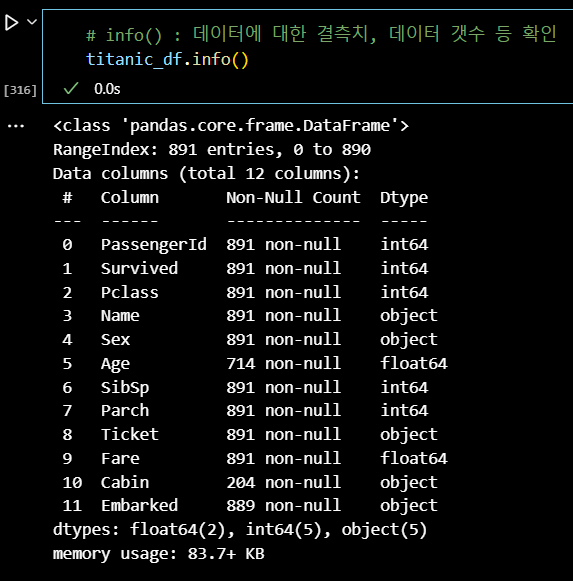
# info() : 데이터에 대한 결측치, 데이터 갯수 등 확인
titanic_df.info()

# 숫자형
    # Age, SibSp, Parch, Fare
# 범주형
    # Pclass, Sex, Cabin, Embarked 
# X 변수 1개, Y 변수 (Survived)

# X 변수 : Fare, Y 변수 : Survived
X_1 = titanic_df[['Fare']]
y_true = titanic_df[['Survived']]

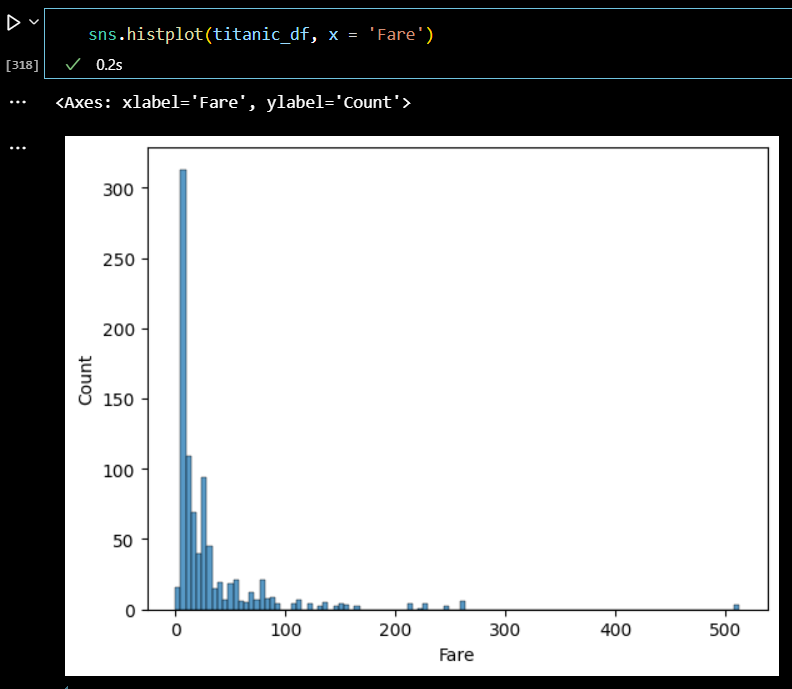
sns.histplot(titanic_df, x = 'Fare')

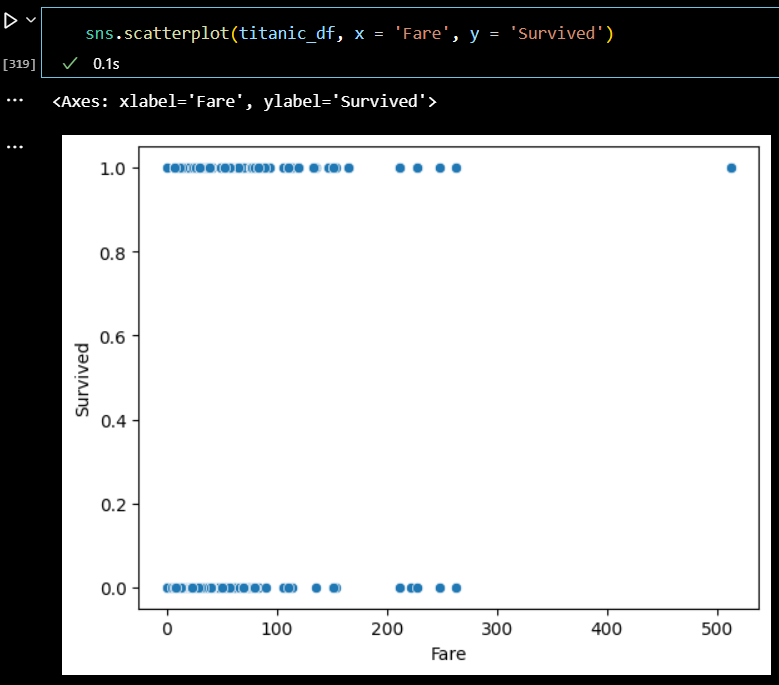
sns.scatterplot(titanic_df, x = 'Fare', y = 'Survived')

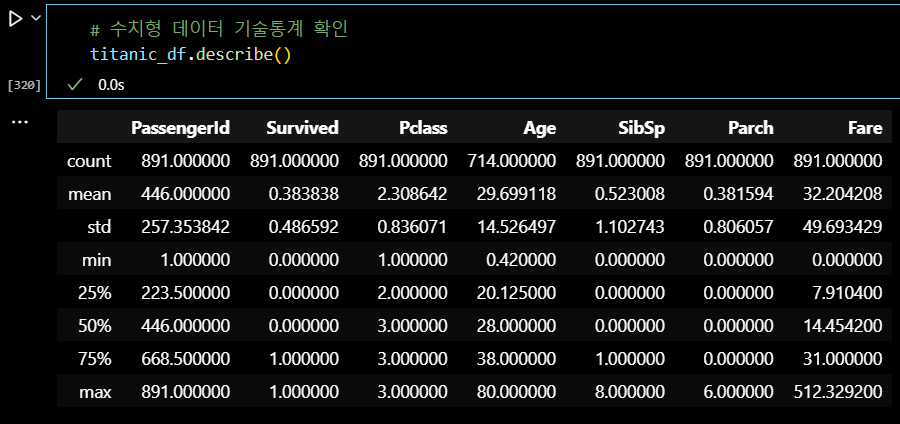
# 수치형 데이터 기술통계 확인
titanic_df.describe()

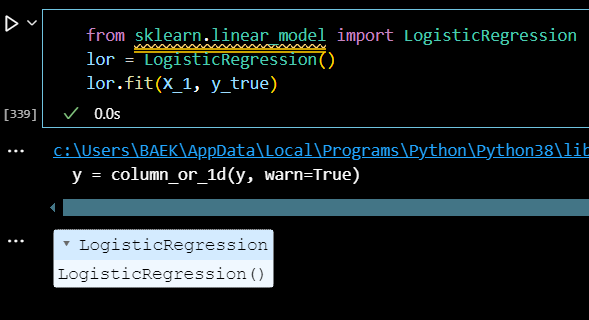
from sklearn.linear_model import LogisticRegression
lor = LogisticRegression()
lor.fit(X_1, y_true)

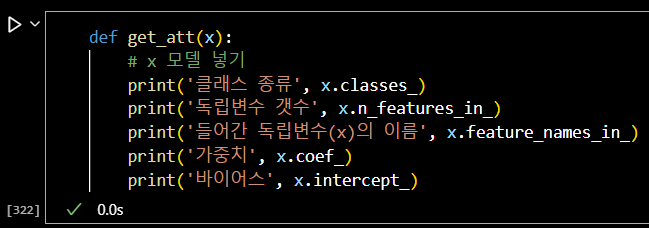
def get_att(x):
    # x 모델 넣기
    print('클래스 종류', x.classes_)
    print('독립변수 갯수', x.n_features_in_)
    print('들어간 독립변수(x)의 이름', x.feature_names_in_)
    print('가중치', x.coef_)
    print('바이어스', x.intercept_)

get_att(lor)

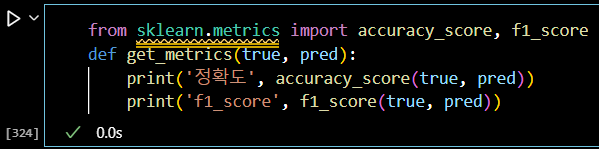
from sklearn.metrics import accuracy_score, f1_score
def get_metrics(true, pred):
    print('정확도', accuracy_score(true, pred))
    print('f1_score', f1_score(true, pred))

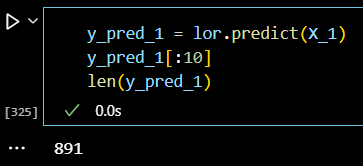
y_pred_1 = lor.predict(X_1)
y_pred_1[:10]
len(y_pred_1)

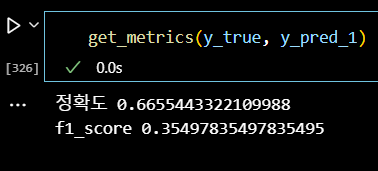
# 평가지표 확인
get_metrics(y_true, y_pred_1)

📌 다중 로지스틱 회귀 실습

다중 로지스틱 회귀는 X 변수의 갯수가 2개 이상일 때 실시하면 된다.

# 숫자형
    # Age, SibSp, Parch, Fare
# 범주형
    # Pclass, Sex, Cabin, Embarked 
# X 변수 1개, Y 변수 (Survived)

# 분석에 활용할 변수 정리
# Y 변수 : Survived
# X 변수(수치형) : Fare
# X 변수(범주형) : Pclass, Sex

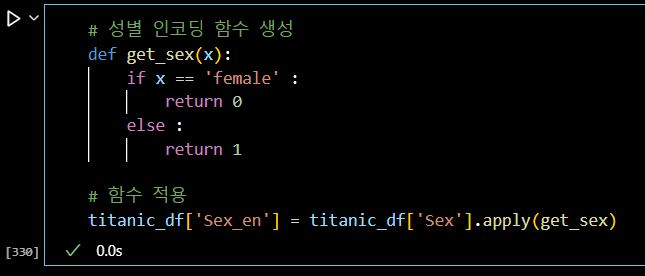
# 성별 인코딩 함수 생성
def get_sex(x):
    if x == 'female' :
        return 0
    else :
        return 1
# 함수 적용
titanic_df['Sex_en'] = titanic_df['Sex'].apply(get_sex)

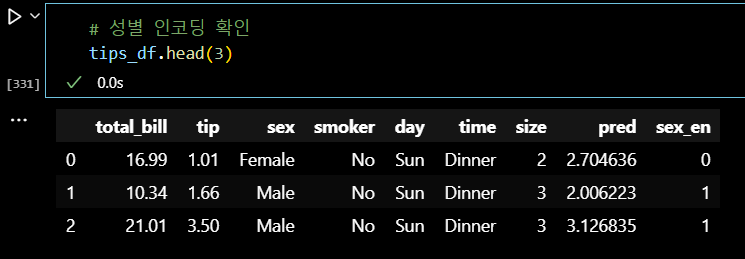
# 성별 인코딩 확인
tips_df.head(3)

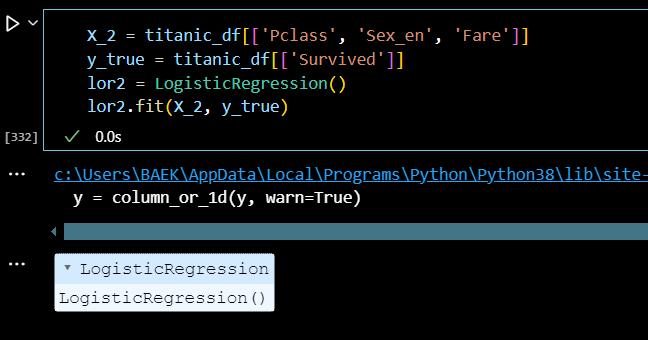
X_2 = titanic_df[['Pclass', 'Sex_en', 'Fare']]
y_true = titanic_df[['Survived']]
lor2 = LogisticRegression()
lor2.fit(X_2, y_true)

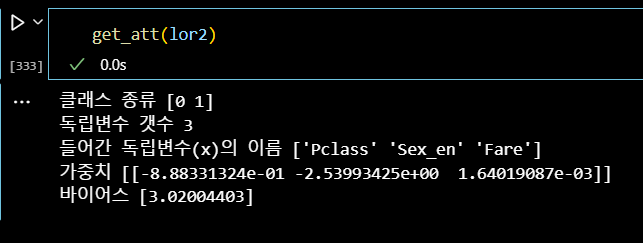
get_att(lor2)

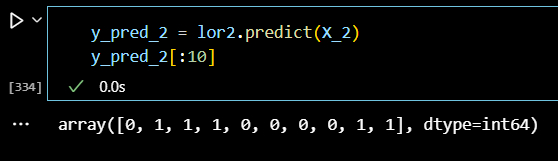
y_pred_2 = lor2.predict(X_2)
y_pred_2[:10]

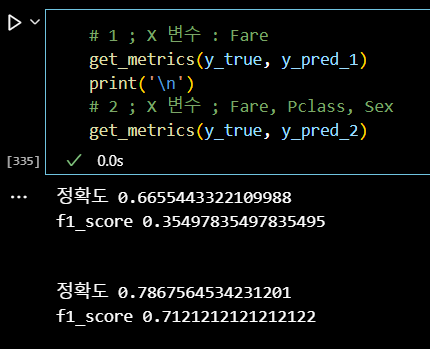
# 1 ; X 변수 : Fare
get_metrics(y_true, y_pred_1)
print('\n')
# 2 ; X 변수 ; Fare, Pclass, Sex
get_metrics(y_true, y_pred_2)

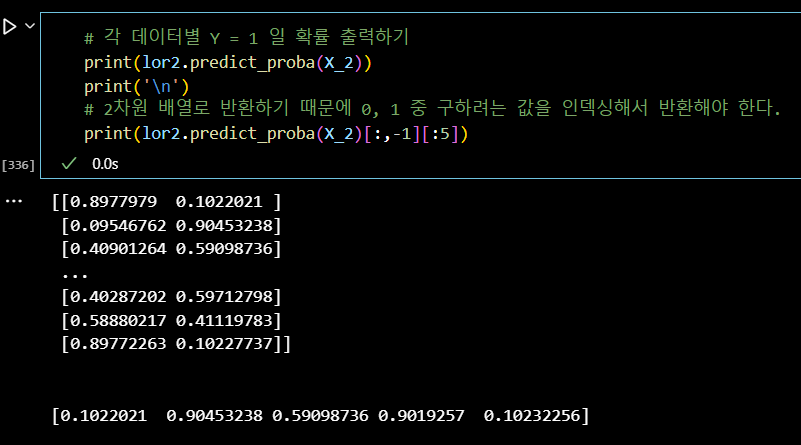
# 각 데이터별 Y = 1 일 확률 출력하기
print(lor2.predict_proba(X_2))
print('\n')
# 2차원 배열로 반환하기 때문에 0, 1 중 구하려는 값을 인덱싱해서 반환해야 한다.
print(lor2.predict_proba(X_2)[:,-1][:5])

📌 참고

# sklearn 버전 확인하기
import sklearn
sklearn.__version__

# sklearn 도움말 불러오기
import sklearn.metrics
help(sklearn.metrics)

📌 회귀, 분류 정리

선형회귀와 로지스틱회귀의 공통점
1. 모델 생성이 쉽다.
2. 가중치(혹은 회귀계수)를 통한 해석이 쉽다.
3. X 변수에 범주형, 수치형 변수 둘 다 사용 가능하다.
선형회귀와 로지스틱 분류 차이점
- Y (종속 변수) : 회귀 (수치형) / 분류 (범주형)
- 평가 척도 : 회귀 (MSE, R^2 ; 선형회귀만) / 분류 (Accuracy, F1 - Score)
- sklearn.모델 :
  회귀 (sklearn.linear_model.linearRegression) /
  분류 (sklearn.linear_model.LogistricRegression)
- sklearn.평가 :
  회귀 (sklearn.metrics.mean_squared_error, r2_score)
  분류 (sklearn.metrics.accuracy_score, f1_score)