[백준] 11052. 카드 구매하기 (Python)

📌 11052. 카드 구매하기

https://www.acmicpc.net/problem/11052

풀이과정

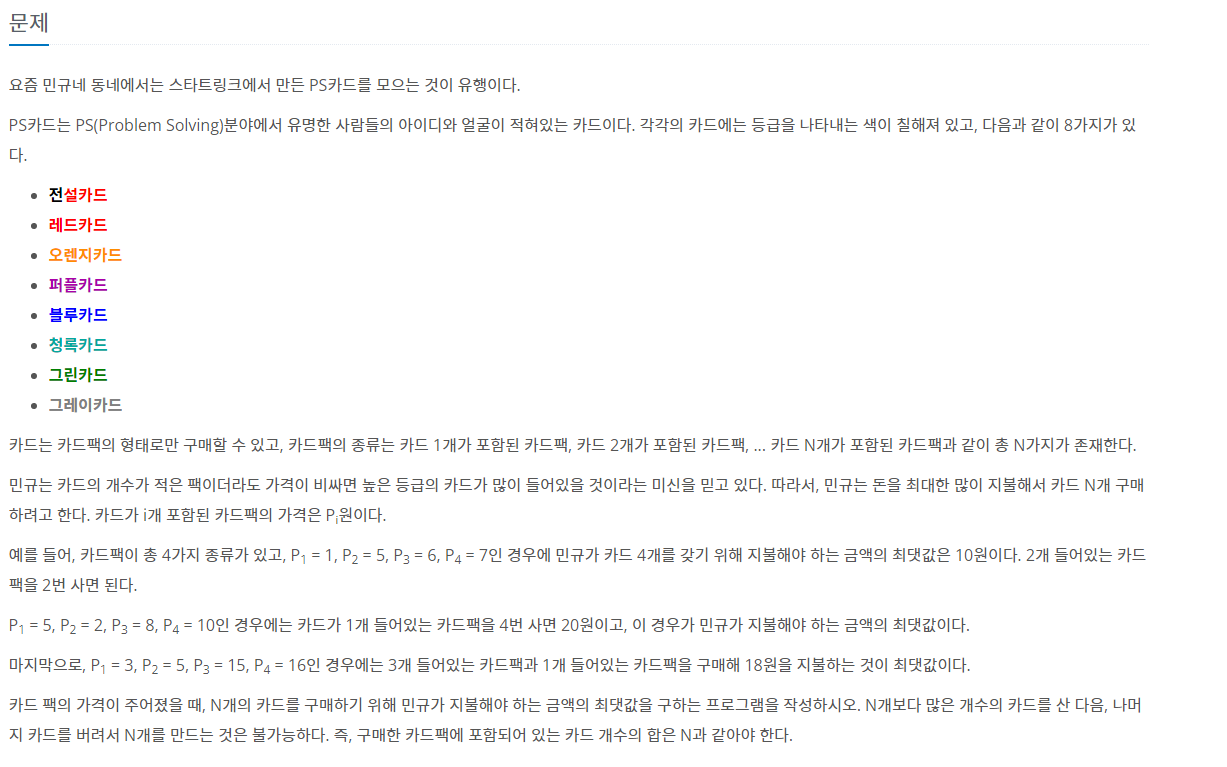
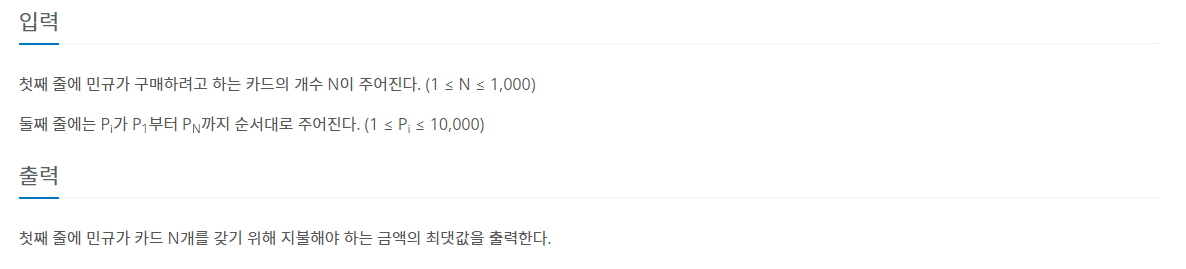
이전의 계산값으로 다음 값을 계산할 수 있을 것 같아서 다이나믹 프로그래밍 알고리즘을 사용하면 될 것이라 생각했다. 처음 아이디어는 바로 전 값을 이용해서 최대 다음 값을 구하고(dp[i-1] + 1), 그 다음에 입력 값 n에 대해서 조합 중 최대 값인 것(dp[i]+dp[n-i])을 찾을 수 있도록 구현했다.

n = int(input())

price = list(map(int, input().split()))

dp = [0]
for i in price:
  dp.append(i)

for i in range(2, n):
  dp[i] = max(dp[i], dp[i-1] + dp[1])

result = 0
for i in range(0, n):
  result = max(result, dp[i]+dp[n-i])

지금 다시 보면 굉장히 터무니 없는 구현 방식이다. 하나를 여러개 살 수 있는 경우를 완전히 배제 해 놓은 알고리즘이다. 따라서 점화식을 다시 생각해서 세워 보았다. Bottom-up 방식으로 구현하려고 하면, dp[i]는 i보다 작은 개수에서(dp[i-j]) price[j]만큼 더한 것이 가장 큰 것이 될 것이다. 좀 말이 어려울 수 있는데, 예를 들어 4개를 사야할 경우 dp[4-1]+price[1], dp[4-2]+price[2], dp[4-3]+price[3], dp[4-4]+price[4] 중 가장 큰 값이 dp[4]가 될 것이고 정답이 될 것이다.

n = int(input())

price = [0] + list(map(int, input().split()))

dp = [0]*(n+1)

for i in range(1, n+1):
 for j in range(1,i+1):
   dp[i] = max(dp[i], dp[i-j] + price[j])

print(dp[n])

✍ 배운 점

1. 점화식을 세울때 dp말고 다른 부가적인 리스트를 사용할 수 도 있다. -> 오히려 쉬운 점화식이 나올 수 도 있다. 점화식 세우는 것이 쉽지 않다면 이 방법도 생각해 보자.

💯 정답

 n = int(input())

price = [0] + list(map(int, input().split()))

dp = [0]*(n+1)

for i in range(1, n+1):
  for j in range(1,i+1):
    dp[i] = max(dp[i], dp[i-j] + price[j])

print(dp[n])