[백준] 2293. 동전 1 (Python)

📌 2293. 동전 1

https://www.acmicpc.net/problem/2293

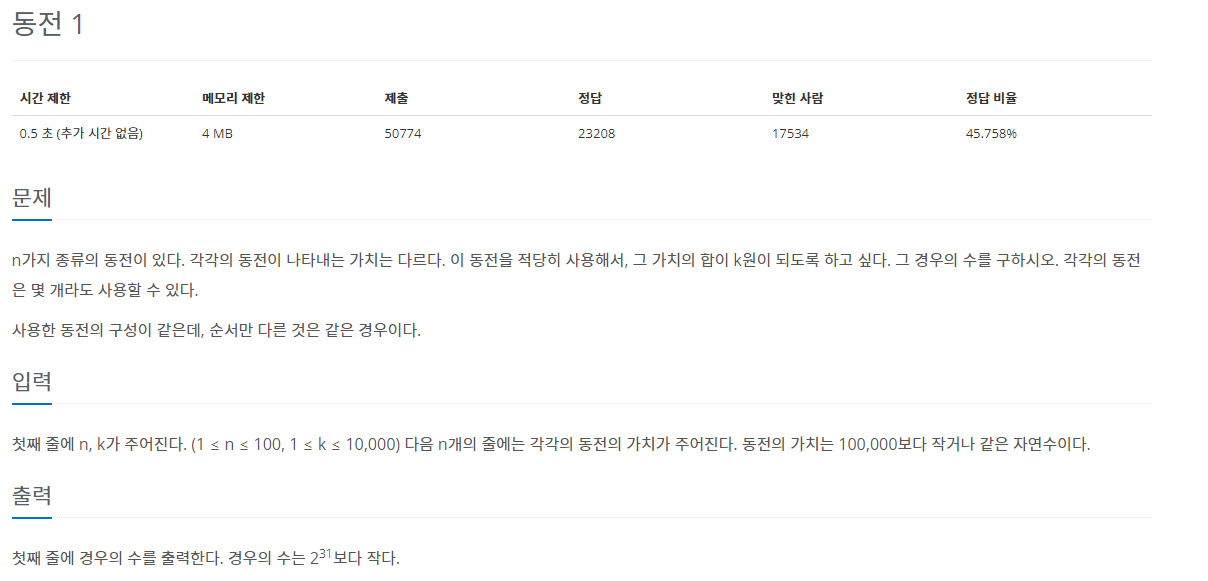
만약, 가지고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수 일 경우, 그리디로 풀면 된다. 예를 들어 100원, 500원, 100원, 50원, 10원으로 주어진 금액을 만드는 경우에는 그리디로 쉽게 풀 수 있다. 하지만 이 문제는 동전의 값이 랜덤으로 주어지므로, 배수일수도, 아닐 수도 있기 때문에 그리디로 풀 수 없다. 이 문제는 전형적인 다이나믹 프로그래밍으로 풀어야 하는 문제이다.

풀이과정

dp로 풀어야 하는 것은 알았지만 어떤 것을 기준으로 점화식을 만들어야 할지가 고민이 되었다. bottom-up 방식으로 금액에서 동전을 하나씩 더하여 만드는 알고리즘을 구현해 보았다.

n, k = map(int, input().split())

coins = []
dp = [0]*(k+1)
for i in range(n):
  coin = int(input())
  coins.append(coin)
  dp[coin] = 1

for i in range(1, k+1):
  for j in coins:
    if i+j<=k and dp[i] != 0:
      dp[i+j] = dp[i]+1
  
print(dp[k])

하지만 제출 결과, '틀렸습니다'가 나왔다. 그 이유를 생각해보았을 때, 이렇게 구현을 하면 똑같은 조합의 경우 중복해서 세게 된다.

따라서 다른 방법을 생각해보았다. 1을 더하는 게 아니라, 금액에서 각 동전만큼 뺀 금액이 만들어지는 경우를 다 더해주면 된다. 아주 작은 차이인데, 이 경우에는 중복된 조합이 포함되지 않을 것이다.

n, k = map(int, input().split())

coins = []
dp = [0]*(k+1)
for i in range(n):
  coin = int(input())
  coins.append(coin)

dp[0] = 1


for j in coins:
  for i in range(j, k+1):
    if i-j>=0 :
      dp[i] += dp[i-j]
  
print(dp[k])

✍ 끄적끄적

(수정 2023.03.03)

for i in range(1, k+1):
  for coin in coins:
    if i-coin>= 0:
      dp[i] += dp[i-coin]

만약 이렇게 코드를 적는다면...
동전들이 중복이 될 것이다. 그래서 경우의 수가 정답보다 훨씬 많이 나오게 된다.
따라서 for문의 순서도 여기서 중요하다.

💯 정답

n, k = map(int, input().split())

coins = []
dp = [0]*(k+1)
for i in range(n):
  coin = int(input())
  coins.append(coin)

dp[0] = 1


for j in coins:
  for i in range(j, k+1):
    if i-j>=0 :
      dp[i] += dp[i-j]
  
print(dp[k])