[백준] 12850 : 본대 산책2 - 분할정복, 행렬, 행렬제곱

---

출처 : 배열에서 이동 acmicpc.net/problem/1981

---

시간 제한	메모리 제한
1초	256 MB

---

문제

n×n짜리의 배열이 하나 있다. 이 배열의 (1, 1)에서 (n, n)까지 이동하려고 한다. 이동할 때는 상, 하, 좌, 우의 네 인접한 칸으로만 이동할 수 있다.

이와 같이 이동하다 보면, 배열에서 몇 개의 수를 거쳐서 이동하게 된다. 이동하기 위해 거쳐 간 수들 중 최댓값과 최솟값의 차이가 가장 작아지는 경우를 구하는 프로그램을 작성하시오.

---

입력

첫째 줄에 n(2 ≤ n ≤ 100)이 주어진다. 다음 n개의 줄에는 배열이 주어진다. 배열의 각 수는 0보다 크거나 같고, 200보다 작거나 같은 정수이다.

---

출력

첫째 줄에 (최대 - 최소)가 가장 작아질 때의 그 값을 출력한다.

---

예제

입력 :

5

1	1	3	6	8
1	2	2	5	5
4	4	0	3	3
8	0	2	3	4
4	3	0	2	1

출력:
2

해설

---

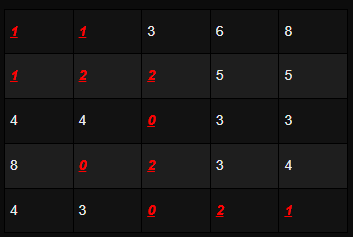
아이디어

출발점(1,1) 부터 도착점 (n,n) 까지 이동하면서, 거쳐간 수의 최대 최소 차가 최소가 되게해야한다.

최솟값을 구해야하므로 나올 수 있는 경우의 수 중에 최대최소 차가 가장 작은것부터 탐색한다.

우선, 출발점과 도착점은 반드시 지나야하므로, 초기 최대최소로 설정해준다.
M(max) : 1, m(min) : 1

출발점부터 현재 최대 최소로 탐색 가능한만큼 완전 탐색한다.
M : 1, m : 1

현재 최대 최소로는 도착점까지 도달하지 못했다.

다음으로 생기는 경우의수는 다음과 같다
M : 3, m : 1, dif(difference) : 2 (new)
M : 2, m : 1, dif : 1 (new)
M : 4, m : 1, dif : 3 (new)

이 중 최대최소 차가 가장 적은 두번쨰 경우로 탐색을 시작한다.
M : 2, m : 1

다음 가능한 경우의 수를 탐색한다
M : 3, m : 1, dif : 2
M : 4, m : 1, dif : 3
M : 5, m : 1, dif : 4 (new)
M : 2, m : 0, dif : 2 (new)

차가 제일 적은 첫번째 경우 탐색
M : 3, m : 1, dif : 2

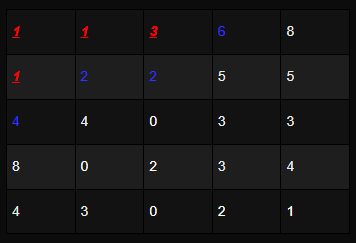
다음 경우의 수
M : 4, m : 1, dif : 3
M : 5, m : 1, dif : 4
M : 2, m : 0, dif : 2
M : 6, m : 1, dif : 5 (new)

차가 제일 적은 세번째 경우 탐색
M : 2, m : 0, dif : 2

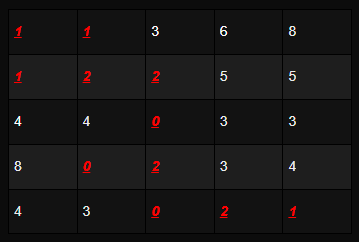
이때,도착지까지 도달했으므로 답은 2가 된다.

좌표와, 최대최소는 쌍으로 되어있으므로 두 정수의 쌍을 표현할 P 클래스를 구현한다. 추후 HashSet으로 방문 체크를 할거라 싱글턴 기법으로 구현해 같은 점에대한 해쉬코드를 같게 해준다.

private static class P{
        public final int x, y;
        
        private P(int x, int y) {
            this.x = x;
            this.y = y;
        }
        
        private static P[][] ps;
        
        static {
            ps = new P[201][201];
        }
        
        public static P get(int x, int y){
            if (ps[x][y] == null){
                return ps[x][y] = new P(x, y);
            }
            return ps[x][y];
        }
    }

경우의수들은 항상 최대최소 차가 가장 적은값을 뽑아야하므로 우선순위 큐로 구현한다.

PriorityQueue<P> queue = new PriorityQueue<>((o1, o2) -> Integer.compare(o1.y - o1.x, o2.y - o2.x));

중복된 최대최소를 경우의수로 생각 할 필요 없으므로 중복체크를 할 HashSet을 구현한다.

HashSet<P> visit = new HashSet<>();

최대 최소 쌍을 골랐을때 출발점으로부터 탐색 할 메소드를 구현한다. 이때 탐색하며 새로 가능한 점을 Set 자료구조로 반환하고, 도착지까지 도착할 경우 null을 반환한다.

private static HashSet<Integer> find(P minmax){
        int min = minmax.x;
        int max = minmax.y;
        
        HashSet<Integer> set = new HashSet<>();
        boolean[][] visit = new boolean[N][N];
        ArrayDeque<P> deque = new ArrayDeque<>();
        deque.addLast(P.get(0,0));
        visit[0][0] = true;
        
        while (!deque.isEmpty()){
            P p = deque.pollFirst();
            if (p.x == N-1 && p.y == N-1)
                return null;

            for (int i = 0; i < 4; i++) {
                int x = p.x + dx[i];
                int y = p.y + dy[i];
                if (x < 0 || y < 0 || x >= N || y >= N) continue;
                if (visit[x][y]) continue;
                if (min <= map[x][y] && map[x][y] <= max){
                    visit[x][y] = true;
                    deque.addLast(P.get(x,y));
                }
                else {
                    set.add(map[x][y]);
                }
            }
        }
        return set;
    }

출발점과 도착점으로 초기 최대 최소쌍을 설정해준다.

P init = P.get(Math.min(map[0][0], map[N-1][N-1]), Math.max(map[0][0], map[N-1][N-1]));

순차적으로 너비 우선 탐색을 할 코드를 구현한다.

HashSet<P> visit = new HashSet<>();
queue.add(init);
visit.add(init);

while (!queue.isEmpty()){
    P p = queue.poll();

    HashSet<Integer> next = find(p);

    if (next == null){
        System.out.println(p.y - p.x);
        break;
    }

    for (Integer i : next) {
        if (i > p.y){
            P nextp = P.get(p.x, i);
            if (visit.contains(nextp)) continue;
            queue.add(nextp);
            visit.add(nextp);
        }
        else if (i < p.x){
            P nextp = P.get(i, p.y);
            if (visit.contains(nextp)) continue;
            queue.add(nextp);
            visit.add(nextp);
        }
    }
}

최악의 경우 100x100개의 쌍이 만들어지고
그래프의 정점이 최대 100x100이므로
O(N^4logN) 100,000,000 x log100(=6.x) 으로 표현되지만, 모든 쌍이 그래프의 모든 점을 탐색하지 않으니 시간안에 들어 올 것 같다.
공간 복잡도는 가능한 쌍의 수와 같아 최대 100x100의 두개의 int쌍이 생겨 공간복잡도는 넉넉하다.

시간 복잡도	공간 복잡도
O(N^4logN)	100x100x8Byte + a

---

코드

github에서 코드 보기 : https://github.com/LuizyHub/CodingTestStudy/blob/master/src/Baek1981.java

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.HashSet;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class Main {
    public static final int[] dx = {-1, 0, 0, 1};
    public static final int[] dy = {0, 1, -1, 0};
    private static class P{
        public final int x, y;
        private P(int x, int y) {
            this.x = x;
            this.y = y;
        }
        private static P[][] ps;
        static {
            ps = new P[201][201];
        }
        public static P get(int x, int y){
            if (ps[x][y] == null){
                return ps[x][y] = new P(x, y);
            }
            return ps[x][y];
        }
    }
    private static int N;
    private static int[][] map;
    private static HashSet<Integer> find(P minmax){
        int min = minmax.x;
        int max = minmax.y;
        HashSet<Integer> set = new HashSet<>();
        boolean[][] visit = new boolean[N][N];
        ArrayDeque<P> deque = new ArrayDeque<>();
        deque.addLast(P.get(0,0));
        visit[0][0] = true;
        while (!deque.isEmpty()){
            P p = deque.pollFirst();
            if (p.x == N-1 && p.y == N-1)
                return null;

            for (int i = 0; i < 4; i++) {
                int x = p.x + dx[i];
                int y = p.y + dy[i];
                if (x < 0 || y < 0 || x >= N || y >= N) continue;
                if (visit[x][y]) continue;
                if (min <= map[x][y] && map[x][y] <= max){
                    visit[x][y] = true;
                    deque.addLast(P.get(x,y));
                }
                else {
                    set.add(map[x][y]);
                }
            }
        }
        return set;
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        map = new int[N][N];
        StringTokenizer st;
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 0; j < N; j++) {
                map[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        P init = P.get(Math.min(map[0][0], map[N-1][N-1]), Math.max(map[0][0], map[N-1][N-1]));
        PriorityQueue<P> queue = new PriorityQueue<>((o1, o2) -> Integer.compare(o1.y - o1.x, o2.y - o2.x));
        HashSet<P> visit = new HashSet<>();
        queue.add(init);
        visit.add(init);

        while (!queue.isEmpty()){
            P p = queue.poll();

            HashSet<Integer> next = find(p);

            if (next == null){
                System.out.println(p.y - p.x);
                break;
            }

            for (Integer i : next) {
                if (i > p.y){
                    P nextp = P.get(p.x, i);
                    if (visit.contains(nextp)) continue;
                    queue.add(nextp);
                    visit.add(nextp);
                }
                else if (i < p.x){
                    P nextp = P.get(i, p.y);
                    if (visit.contains(nextp)) continue;
                    queue.add(nextp);
                    visit.add(nextp);
                }
            }
        }
    }
}

---

결론

지난번 아기상어 문제처럼 우선순위 큐를 이용한 너비우선 탐색을 진행하였다.
개선할 점으로는 매번 새로운 탐색을 진행하므로 이전 상황을 메모해두면 이전 상황부터 탐색을 진행해, 탐색 부분에서 속도를 줄일 수 있을 것 같다. 맵 사이즈가 최대 100x100이기 때문에 이 문제에서는 문제가 되지는 않았다.
대부분 사람들은 주어지는 숫자가 200이하 자연수인점을 이용해서 이분탐색(투 포인터)를 이용해 최소 해를 찾았다. 주어지는 수의 범위가 컸다면 내가 풀었던 방식으로 풀어야 할 것같다.