하루에도 여러 번 Ctrl + F 해서 검색하는 일이 있다.
어떻게 동작하는 지 고민해본 적이 없는데 여기에도 여러 알고리즘이 있다.
그 중 KMP 알고리즘을 소개한다. KMP는 만든 사람들의 이름의 첫 글자를 따서 만든 이름이다.
이 글에서는 별 말이 없으면 길이 n인 Text에서 길이 m인 Pattern(n>m)을 검색하는 상황이고, i, j는 각각 Text와 Pattern의 인덱스이다.
Brute Force
먼저 Naive Algorithm이라고도 불리는 Brute Force 방법을 살펴보자.
Text와 Pattern을 제일 앞부터 한 글자 씩 비교한다.
모두 일치하면 결과에 저장하고, Pattern을 한 칸 오른쪽으로 밀어준 후, 다시 제일 앞부터 비교한다.
불일치가 발생하면 Pattern을 한 칸 오른쪽으로 밀어준 후, 다시 제일 앞부터 비교한다.
- 첫 글자를 맞춰두고 시작(i=0, j=0)
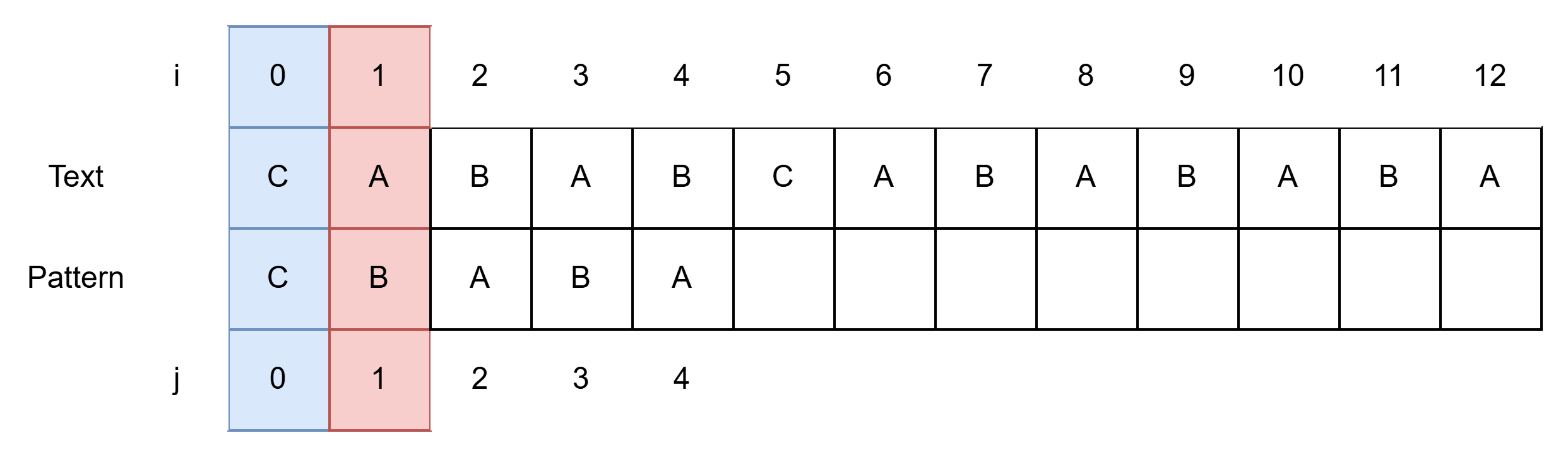
- 첫 글자 일치하여 i, j 각각 1씩 증가
- 불일치 발생
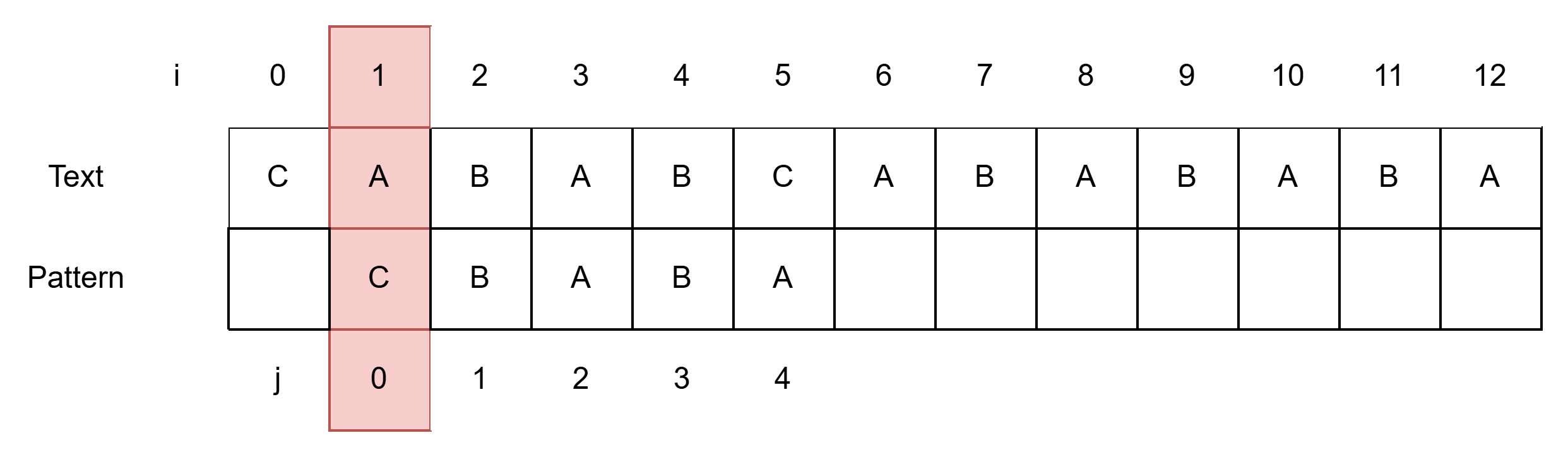
- Pattern을 한 칸 밀어주고(i = 1, j = 0) 다시 탐색 시작
- 위 과정을 반복
Brute Force의 경우 불일치가 발생하면 Pattern을 항상 한 칸씩 밀어주고 다시 Pattern의 처음부터 탐색을 시작한다.
Pattern의 마지막에서 불일치가 발생하는 경우 m번 비교를 하게 되며,
Text 길이가 n이므로 시간 복잡도는 O(mn)이다.
KMP Algorithm
Pattern을 한 번에 여러 칸 밀어주고, Pattern의 처음이 아닌 중간부터 일치 여부를 따지면 훨씬 효율적이다. 어떻게 하면 답을 놓치지 않으면서 이를 구현할 수 있을 지 KMP 알고리즘의 작동 방식을 살펴보자.
바로 구체적인 예시를 살펴보자.
예시
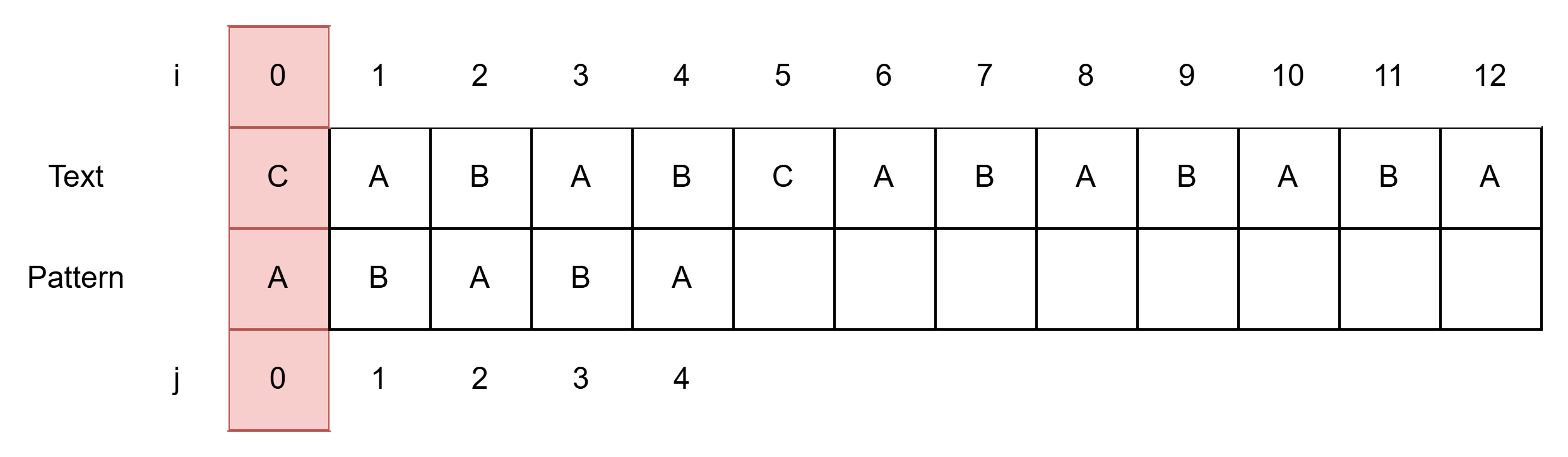
- i = 0, j = 0으로 시작하여 둘을 비교한다.
- Pattern의 처음부터 불일치 발생한 경우 즉, j=0에서 불일치 발생
- i를 1 증가해준다. (i, j를 같은 위치에 둘 것이니 아래 Pattern 종이를 한 칸 오른쪽으로 밀어준다.)
- i = 1, j = 0 이 되어 둘을 비교한다.
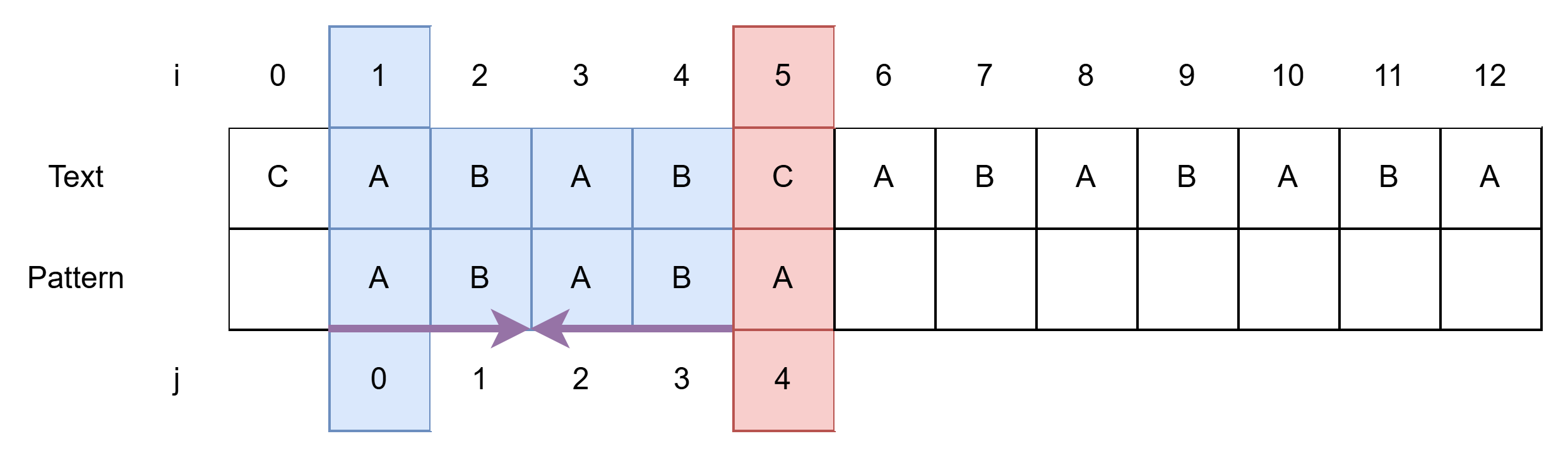
- i = 1, j = 0에서 시작한다.
- 일치하는 경우 i, j 를 각각 1씩 증가하다가 불일치하면 멈춘다.
- i = 5, j = 4에서 멈춘다.
- 불일치가 발생하고 j ≠ 0인 경우, 그 직전까지는 일치했다는 것으로, 그 정보를 최대한 이용한다.
- 앞 뒤가 같은 최대 부분을 찾아준다. 그것을 보라색 화살표로 나타냈다.
- 보라색 화살표 부분이 일치하므로 Pattern을 2칸 밀 수 있다.
- 불일치 발생한 직전 j =3부터 살펴보면 j = 0~1, j = 2~3 부분이 일치한다.
- j = 1의 B가 j = 3의 B 자리에 오는 것이므로 2칸 밀어준다.(2칸인건 화살표 길이와 별개다!)
- Pattern을 2칸 민다는 것은 j를 2 감소 시킨다는 것이다.
- 따라서 j = 2가 되며, i = 5, j = 2를 비교한다.
- Brute Force에서는 1칸 밀 것을 2칸 한 번에 밀 수 있는 것이다.
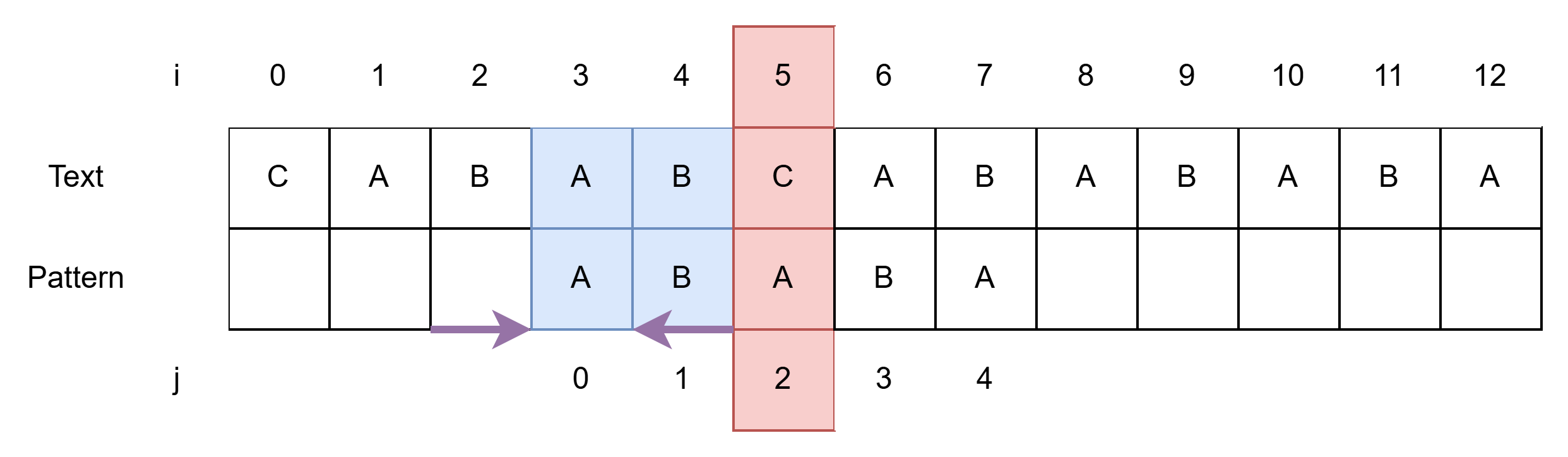
- i = 5, j = 2에서 시작한다.
- Pattern의 앞 부분(j = 0~1)은 이미 일치하므로 살펴볼 필요 없이 j = 2부터 살펴본다.
- 시작(j = 2)부터 바로 불일치한다.
- 불일치가 발생하고 j ≠ 0인 경우, 앞 뒤가 같은 최대 부분을 찾아준다.
- 지금은 같은 부분이 없다. (Pattern의 뒤부터 B, AB와 같은 것이 앞쪽에 있는 지 살펴보면 자기 자신 제외 없다.)
- j = -1의 빈 문자가 j = 1의 B 자리에 오도록 Pattern을 2칸 밀어준다.
- 즉, j 값이 2 감소하여 j = 0이 되어, i = 5, j = 0을 비교한다.
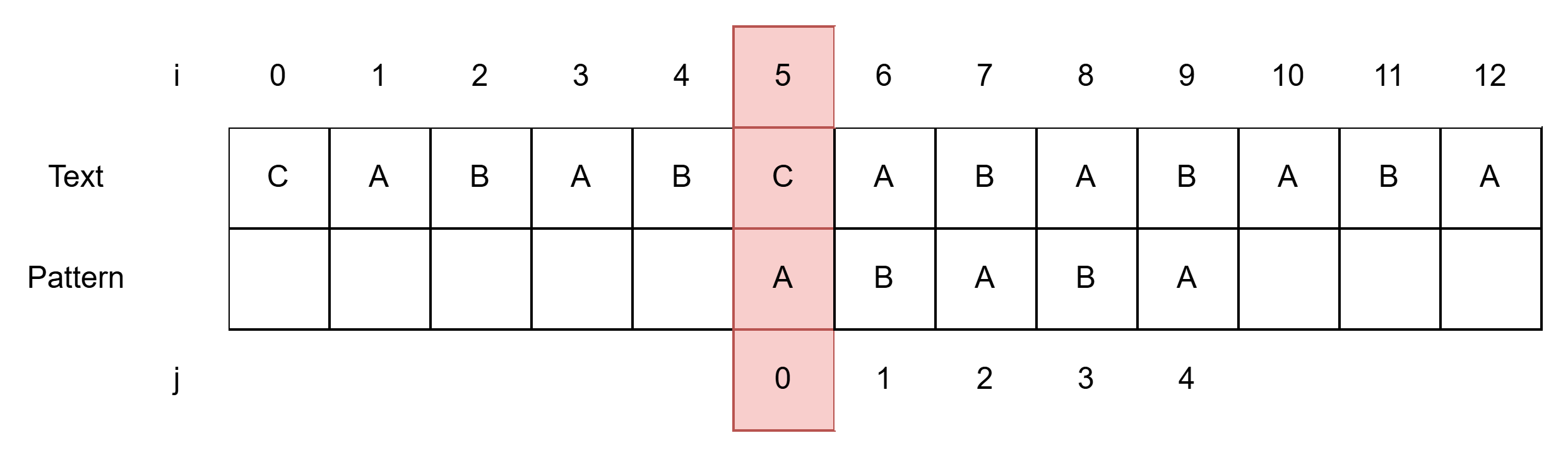
- i = 5, j =0에서 시작한다.
- 시작부터 바로 불일치한다.
- Pattern의 처음부터 불일치 발생한 경우 즉, j=0에서 불일치 발생
- i를 1 증가해준다. (i, j를 같은 위치에 둘 것이니 아래 Pattern 종이를 한 칸 오른쪽으로 밀어준다.)
- i = 6, j = 0이 되어 이 둘을 비교한다.
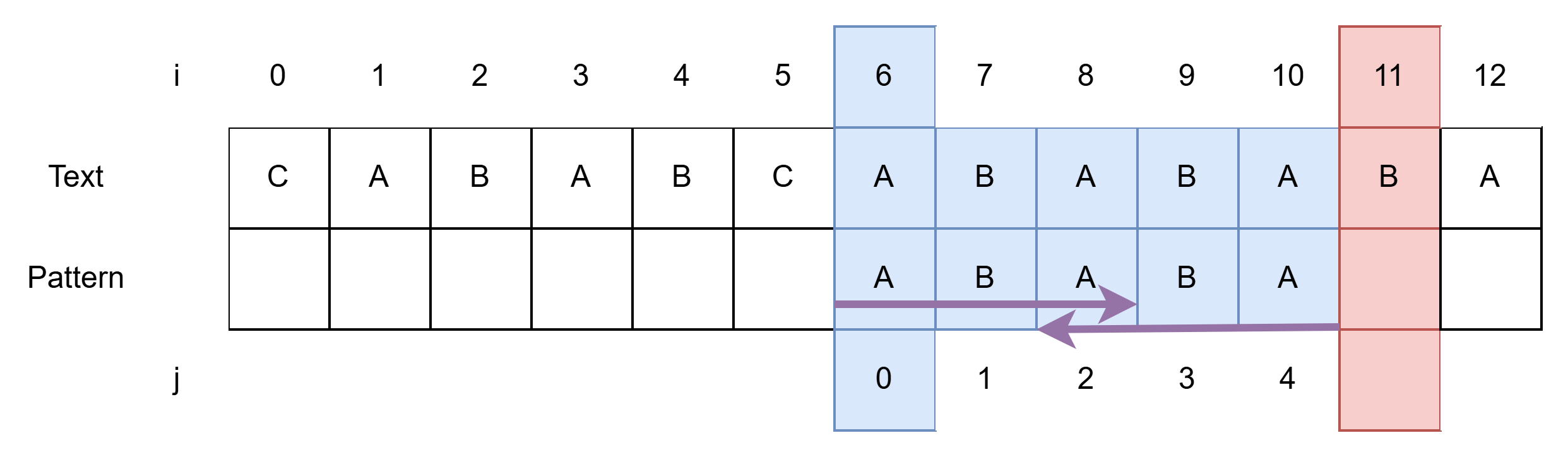
- i = 6, j = 0에서 시작한다.
- 일치하면 i, j 를 각각 1 증가한다.
- i = 11, j = 5에서 멈춘다.
- 모두 일치하므로 결과에 저장한다.
- j가 Pattern의 길이인 5가 되면 모두 일치하는 것이다.(j == m)
- 얼마나 옮길 지 정하기 위해 앞 뒤가 같은 최대 부분을 찾아준다.
- Pattern을 2칸 밀어준다.
- j = 0~2, j = 2~4 부분이 일치한다.
- 따라서 j = 2의 A가 j = 4의 A 자리에 와야 하므로 Pattern을 2칸 밀어준다.
- 즉, j는 2 감소하여 i = 11, j = 3이 된다.
- Pattern을 2칸 밀어준다.

- i = 11, j = 3에서 시작
- 일치하므로 i, j 각각 1 증가
- i = 13, j = 5에서 멈춘다
- 모두 일치(j == m)하므로 결과를 저장한다.
- 얼마나 옮길 지 정하면 위와 마찬가지로 Pattern을 2칸 밀어주게 된다.
- 이후 일치 탐색을 하면 i 값이 n=12를 벗어나므로 모든 탐색을 종료한다.
핵심
- i는 작아지지 않는다.
- 부분 일치하는 경우 Pattern을 한 번에 여러 칸 옮길 수 있어 효율적이다.
- 부분 일치하는 경우 Pattern을 처음부터 살펴보지 않아 효율적이다.
- 시각적으로 Pattern을 미는 행위는 j 값을 감소하는 것인데, 얼마나 줄일지 미리 알고 있어야 한다.
- 매번 j를 얼마나 줄일지 계산한다면 Brute Force와 별 차이가 없다.
LPS Table
어떤 것인가
- Pattern을 얼마나 밀어야 하는 지 즉, j 값을 얼마로 줄일 지 미리 계산해둔 것을 LPS Table이라 한다.
- LPS는 Longest Proper Prefix which is also Suffix의 약자이다.
- 그러니까 앞 뒤가 같은 부분 중 가장 긴 것을 찾는다는 것이다.
위의 예시를 잠시 살펴보면
예시1
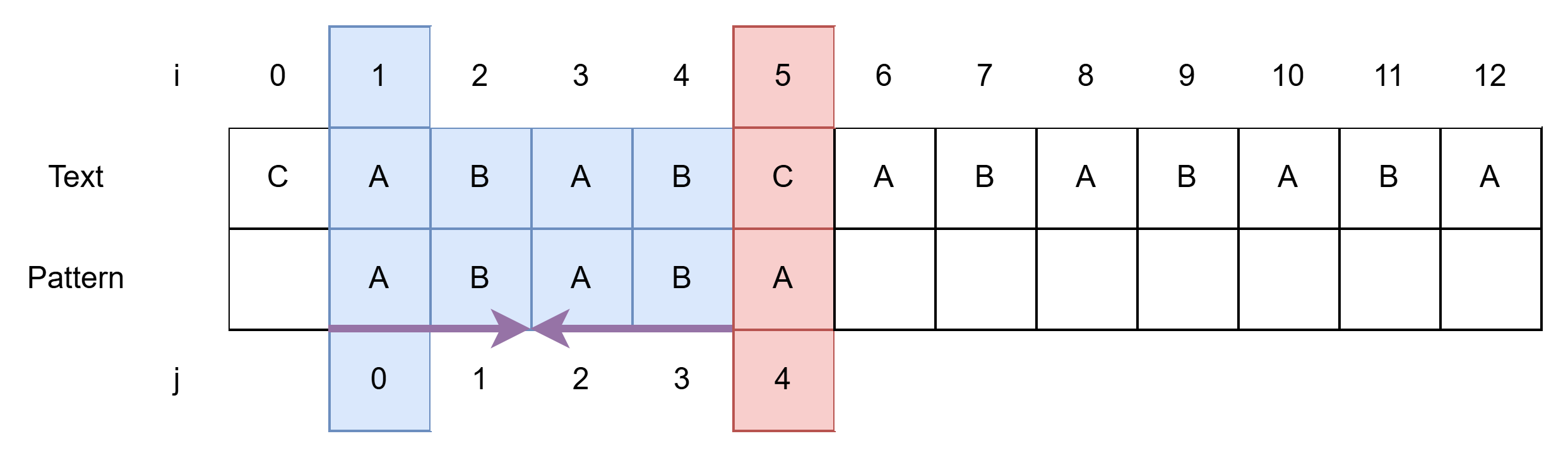
- i = 5, j = 4일 때 불일치 발생
- 마지막 일치는 j = 3인 B이고, 이 자리에 j = 1인 B가 올 것이고,
- 빨간 표시에서 다음 비교를 진행할 때 i = 5, j = 2가 되어야 한다.
- 그러니까, j = 4일 때 불일치 했다면, LPS[j - 1] = LPS[3] = 2가 되어야한다.
예시2
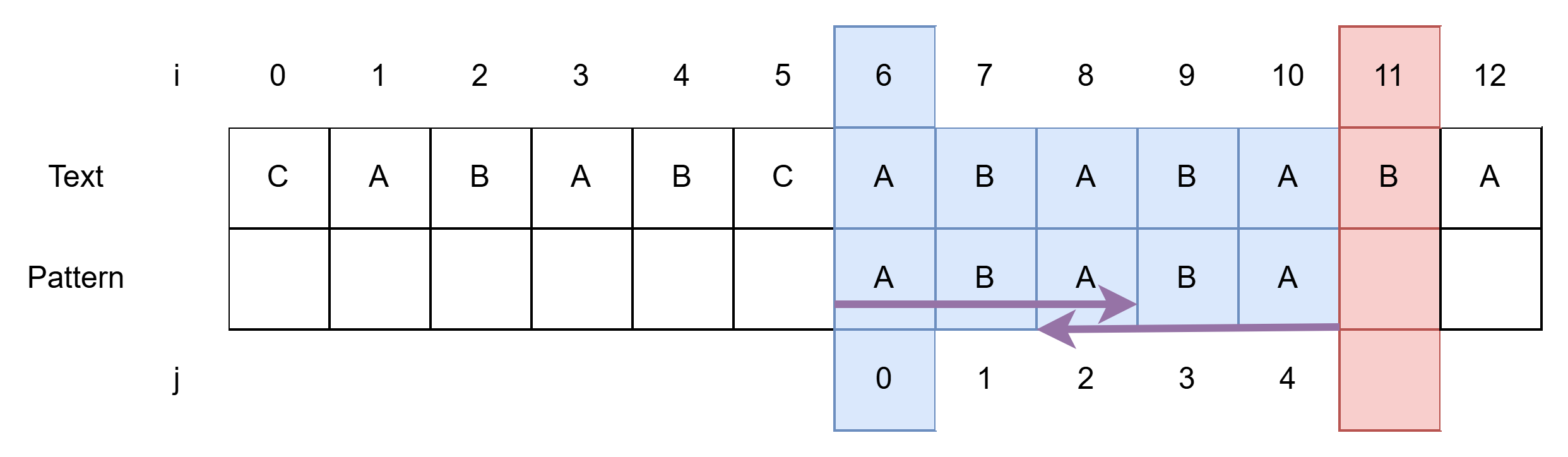
- i = 11, j = 5일 때 모두 일치
- 마지막 일치는 j =4인 A이고, 이 자리에 j = 2인 A가 올 것이고,
- 빨간 표시에서 다음 비교를 진행할 때 i = 11, j = 3이 되어야 한다.
- 그러니까, j = 5일 때 불일치 했다면 LPS[j - 1] = LPS[4] = 3이 되어야 한다.
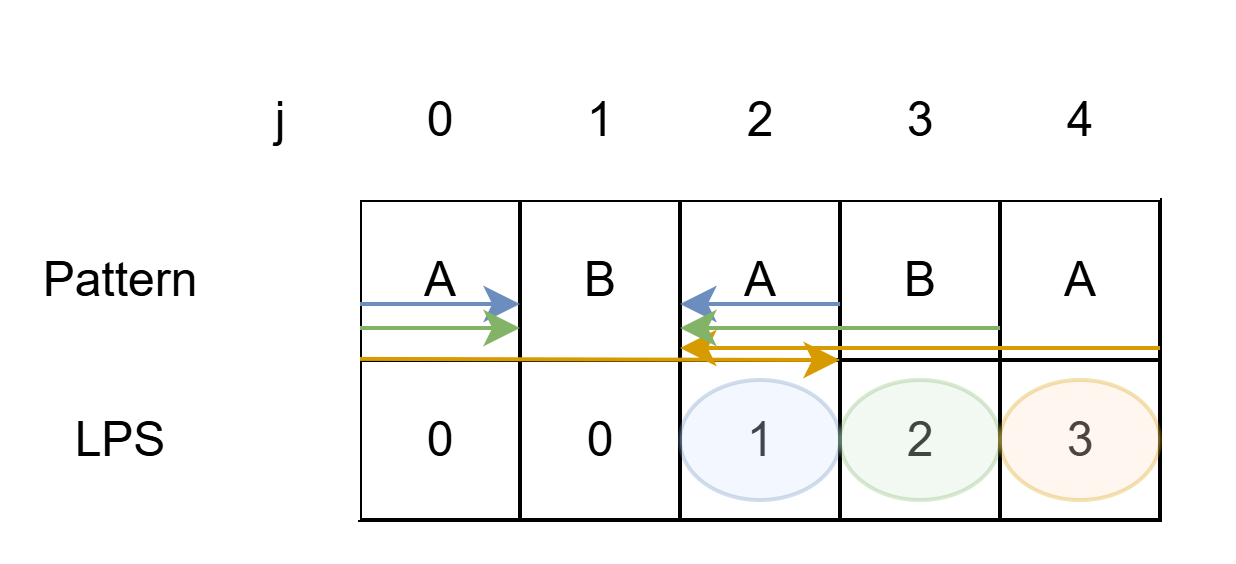
ABABA의 LPS Table
- 위 예시를 잘 생각해보면, 아래와 같은 LPS Table을 만들 수 있다.
- 결국, 순서대로 A, AB, ABA, ABAB, ABABA라는 문자열을 보면서, 접두사이면서 접미사인 것 중 가장 긴 것의 길이를 기록하는 것이다.
- A랑 AB는 접두사이면서 접미사인 것이 없으므로 0.(자기 자신은 제외하고 생각한다.)
- ABA는 A가 접두사이며 접미사이므로 그 길이는 1
- ABAB는 AB가 접두사이며 접미사이므로 그 길이는 2
- ABABA는 ABA가 접두사이며 접미사이므로 그 길이는 3
Boyer Moore Algorithm
그런데, 재밌는 점이 있다.
아래 예시를 보자.
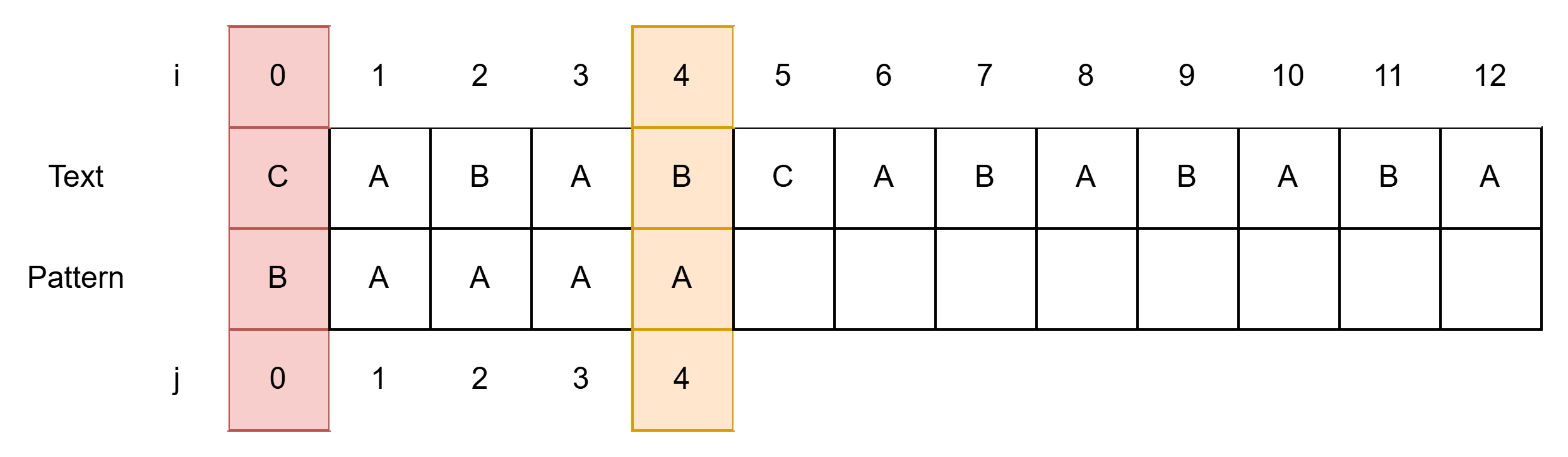
pattern의 앞 부분부터 살펴보았는데 바로 불일치하고, 이 경우 pattern을 한 칸 밀어주게 된다.
그런데 pattern의 뒷 부분부터 살펴보면 어떤가?
Text의 B와 일치하려면 Pattern에 B가 j = 0에만 있으므로 4칸을 밀어줄 수 있다.
우리가 Pattern을 오른쪽으로 밀기 때문에, Pattern의 왼쪽이 아닌 오른쪽부터 일치를 따지는 것이 더 효율적인 것이다!
이를 이용해서 만든 것이 KMP보다 일반적으로 더 성능이 좋은 Boyer Moore Algorithm이다.
다음에 기회가 되면 Boyer Moore Algorithm에 대해 소개하겠다.